Modelo simple

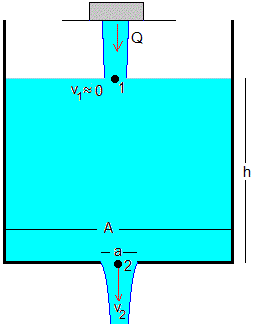
Un depósito cilíndrico abierto por la parte superior de sección A, tiene un orificio de sección a en la parte inferior por el cual se escapa un volumen de líquido av₂ por unidad de tiempo. Siendo v₂ la velocidad de salida del líquido por el orificio

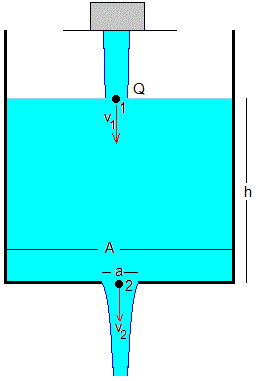
Por otra parte, un flujo Q de líquido proveniente de un grifo llena el depósito.

La altura del líquido en el depósito en el instante t=0 es h₀. En este apartado, determinaremos la altura h en función del tiempo t y la altura final en el estado estacionario, h_∞

La evolución de la altura de líquido en el depósito es

${\displaystyle A\frac{dh}{dt}=Q-a{v}_2}$

Aplicamos la ecuación de Bernoulli para determinar la velocidad v₂ de salida del líquido por el orificio

${\displaystyle \begin{array}{l}{p}_1+\rho g{y}_1+\frac{1}{2}\rho v_1^2=p_2+\rho g{y}_2+\frac{1}{2}\rho v_2^2\\ p_0+\rho g\left(y_1-y_2\right)+\frac{1}{2}\rho v_1^2=p_0+\rho g+\frac{1}{2}\rho v_2^2\end{array}}$

p₀ es la presión atmosférica, y₁-y₂=h y v₁=-dh/dt. El resultado es

${\displaystyle 2gh+{\left(\frac{dh}{dt}\right)}^2=v_2^2}$

Eliminando v₂ en el sistema de dos ecuaciones

${\displaystyle \begin{array}{l}{\left(\frac{Q}{a}-\frac{A}{a}\frac{dh}{dt}\right)}^2=2gh+{\left(\frac{dh}{dt}\right)}^2\\ \left(\frac{A^2}{a^2}-1\right){\left(\frac{dh}{dt}\right)}^2-2Q\frac{A}{a^2}\frac{dh}{dt}+\frac{Q^2}{a^2}-2gh=0\end{array}}$

Expresamos esta ecuación en términos de magnitudes adimensionales

${\displaystyle \begin{array}{l}\alpha =\frac{Q}{A\sqrt{g{h}_0}},r=\frac{1}{2}\left(\frac{A^2}{a^2}-1\right)\\ z=\frac{h}{h_0},\tau =t\sqrt{\frac{g}{h_0}}\end{array}}$

La ecuación diferencial se convierte en

${\displaystyle \begin{array}{l}2r{\left(\frac{h_0}{\sqrt{\frac{h_0}{g}}}\frac{dz}{d\tau }\right)}^2-2A\sqrt{g{h}_0}\alpha \frac{A}{a^2}\frac{h_0}{\sqrt{\frac{h_0}{g}}}\frac{dz}{d\tau }+\frac{A^{2}g{h}_0{\alpha }^2}{a^2}-2g{h}_{0}z=0\\ 2r{\left(\frac{dz}{d\tau }\right)}^2-2\left(2r+1\right)\alpha \frac{dz}{d\tau }+\left(2r+1\right){\alpha }^2-2z=0\\ \frac{dz}{d\tau }=\frac{\left(2r+1\right)\alpha -\sqrt{2r\left(2r+1\right){\alpha }^2+2z}}{2r}\end{array}}$

Solamente es válida el signo - en la solución de la ecuación de segundo grado.

Estado estacionario

En el estado estacionario, dz/dτ=0, de alcanza la altura z_∞

${\displaystyle \begin{array}{l}\left(2r+1\right)\alpha -\sqrt{2r\left(2r+1\right){\alpha }^2+2z_{\infty }}\\ \left(4r^2+4r+1\right){\alpha }^2=\left(4r^2+2r\right){\alpha }^2+2z_{\infty }\\ z_{\infty }=\left(r+\frac{1}{2}\right){\alpha }^2\end{array}}$

Si z_∞=1, la altura de líquido en el depósito no cambia. El valor crítico de α_c es

${\displaystyle {\alpha }_c=\sqrt{\frac{2}{2r+1}}}$

Un valor mayor del α (o del flujo Q) implica una mayor altura z_∞ de líquido en el depósito y un α menor, implica una altura final menor

Desde el estado inicial al estado estacionario

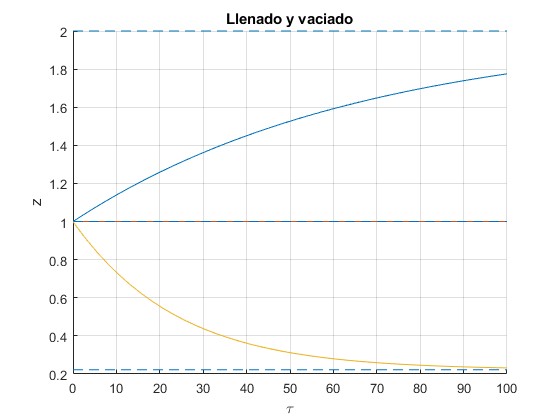
Para determinar la evolución desde el instante inicial τ=0, z=1, hasta el estado estacionario resolvemos la ecuación diferencial por procedimientos numéricos

El cociente de secciones orificio/depósito es a/A=0.3. Representamos z(τ) para tres valores de α (flujo Q)

r=(1/0.3^2-1)/2; %a/A=0.3
alfa_c=sqrt(2/(2*r+1));
hold on
for alfa=[0.6,alfa_c,0.2]
    f=@(t,x) ((2*r+1)*alfa-sqrt(2*r*(2*r+1)*alfa^2+2*x))/(2*r); 
    [t,x]=ode45(f,[0,100],[1,0]); 
    plot(t,x(:,1))
    zf=(r+1/2)*alfa^2;
    line([0,100],[zf,zf],'lineStyle','--')
end
hold off
grid on
xlabel('\tau')
ylabel('z')
title('Llenado y vaciado')

Modelo elaborado

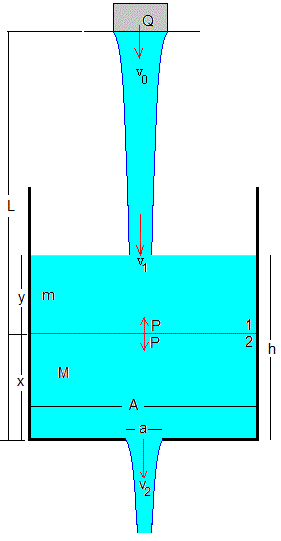
Supondremos un fluido ideal, incompresible, de densidad ρ. La sección del depósito cilíndrico es A, y la sección del orificio de salida es a. La parte inferior del depósito esta a una altura L por debajo del grifo que aporta un flujo constante Q (m³/s) de líquido al depósito.

La altura inicial t=0, de líquido en el depósito es h₀. En este instante se abre el grifo y el orificio en la parte inferior del depósito.

Se divide el depósito en dos subsistemas de alturas y y x de masas m=ρgAy y M=ρgAx, respectivamente

En el intervalo de tiempo dt, el primer susbsistema incrementa su masa en dm, mientras el segundo subsistema se vacía a través del orificio de sección a

En la figura, se señala (en color rojo) la superficie de separación entre los dos subsistemas y la fuerza PA que ejerce el uno sobre el otro, iguales y de sentido contrario

El líquido proveniente del grifo llega al superficie libre del depósito con velocidad v₁ que obtenemos aplicando la ecuación de Bernoulli

${\displaystyle \begin{array}{l}{p}_0+\rho g{y}_0+\frac{1}{2}\rho v_0^2=p_1+\rho g{y}_1+\frac{1}{2}\rho v_1^2\\ v_1^2=v_0^2+2g\left(y_1-y_0\right)=v_0^2+2g\left(L-h\right)\end{array}}$

• Subsistema 1

La altura y del primer subsistema se incrementa debido al aporte del flujo Q

${\displaystyle \frac{dy}{dt}=\frac{Q}{A}}$

Una masa m se mueve con velocidad v=dx/dt<0 (velocidad de la línea divisoria entre los dos subsistemas). A la vez, una masa dm líquido procedente del grifo que se mueve con velocidad -v₁ y se mezclan (choque inelástico)

El momento lineal en el instante t es

${\displaystyle p=mv-v_{1}dm,v=\frac{dx}{dt}}$

El momento lineal en el instante t+dt es

${\displaystyle p+dp=\left(m+dm\right)\left(v+dv\right)\approx mv+mdv+vdm}$

El cambio de momento lineal entre el instante t y t+dt es

${\displaystyle dp=mdv+vdm+v_{1}dm}$

Aplicamos la segunda ley de Newton. Las fuerza externas son el peso y la fuerza que ejerce la presión P en la superficie de separación entre los dos subsistemas

${\displaystyle \begin{array}{l}\frac{dp}{dt}=-mg+PA\\ m\frac{d^{2}x}{dt}+\left(\frac{dx}{dt}+v_1\right)\frac{dm}{dt}=-mg+PA\\ PA=m\left(\frac{d^{2}x}{d{t}^2}+g\right)+\left(\frac{dx}{dt}+v_1\right)\frac{dm}{dt}\end{array}}$

• Subsistema 2

La ecuación de continuidad

${\displaystyle A\frac{dx}{dt}=-a{v}_2}$

Para describir el vaciado del subsistema 2, aplicamos la ecuación de Bernoulli para el estado no estacionario. El punto A esta en el fondo del recipiente y el punto B en la superficie divisoria de ambos subsistemas

${\displaystyle \begin{array}{l}\left(p_A+\rho g{y}_A+\frac{1}{2}\rho v_A^2\right)-\left(p_B+\rho g{y}_B+\frac{1}{2}\rho v_B^2\right)=\frac{dQ}{dt}{\displaystyle \underset{A}{\overset{B}{\int }}\frac{ds}{A(s)}}\\ \left(0+0+\frac{1}{2}\rho v_2^2\right)-\left(P+\rho gx+\frac{1}{2}\rho {\left(\frac{dx}{dt}\right)}^2\right)=\frac{d\left(\rho \frac{dx}{dt}A\right)Q}{dt}\frac{x}{A}\\ \frac{1}{2}\rho A\left(v_2^2-{\left(\frac{dx}{dt}\right)}^2\right)-PA-Mg=M\frac{d^{2}x}{d{t}^2}\end{array}}$

Teniendo en cuenta la ecuación de continuidad y la expresión de la fuerza PA de interacción mutua entre ambos subsistemas

${\displaystyle \frac{1}{2}\rho A\left(\frac{A^2}{a^2}-1\right){\left(\frac{dx}{dt}\right)}^2-m\left(\frac{d^{2}x}{d{t}^2}+g\right)-\left(\frac{dx}{dt}+v_1\right)\frac{dm}{dt}-Mg=M\frac{d^{2}x}{d{t}^2}}$

Sabiendo que m=ρgAy y M=ρgAx

${\displaystyle \begin{array}{l}\frac{1}{2}\rho A\left(\frac{A^2}{a^2}-1\right){\left(\frac{dx}{dt}\right)}^2-\rho Ay\left(\frac{d^{2}x}{d{t}^2}+g\right)-\left(\frac{dx}{dt}+v_1\right)\rho A\frac{dy}{dt}-\rho gAx=\rho Ax\frac{d^{2}x}{d{t}^2}\\ r{\left(\frac{dx}{dt}\right)}^2-\left(x+y\right)\left(g+\frac{d^{2}x}{d{t}^2}\right)-\left(\frac{dx}{dt}+v_1\right)\frac{dy}{dt}=\mathrm{0,}r=\frac{1}{2}\left(\frac{A^2}{a^2}-1\right)\end{array}}$

Teniendo en cuenta que

${\displaystyle \begin{array}{l}x+y=h\\ A\frac{dy}{dt}=Q,\frac{dx}{dt}=\frac{dh}{dt}-\frac{Q}{A},\frac{d^{2}y}{d{t}^2}=0\end{array}}$

Por ser el flujo Q constante. Obtenemos la ecuación diferencial en h

${\displaystyle r{\left(\frac{dh}{dt}-\frac{Q}{A}\right)}^2-h\left(g+\frac{d^{2}h}{d{t}^2}\right)=\left(\frac{dh}{dt}-\frac{Q}{A}+\sqrt{v_0^2+2g\left(L-h\right)}\right)\frac{Q}{A}}$

Escribimos esta ecuación diferencial en términos de magnitudes adimensionales

${\displaystyle \begin{array}{l}\alpha =\frac{Q}{A\sqrt{g{h}_0}},\beta =\frac{v_0^2+2gL}{g{h}_0}\\ z=\frac{h}{h_0},\tau =t\sqrt{\frac{g}{h_0}}\end{array}}$

Se obtiene la ecuación diferencial

${\displaystyle \begin{array}{l}r{\left(\frac{h_0}{\sqrt{\frac{h_0}{g}}}\frac{dz}{d\tau }-\alpha \sqrt{h_{0}g}\right)}^2-h_{0}z\left(g+\frac{h_0}{\frac{h_0}{g}}\frac{d^{2}z}{d{\tau }^2}\right)=\left(\frac{h_0}{\sqrt{\frac{h_0}{g}}}\frac{dz}{d\tau }-\alpha \sqrt{h_{0}g}+\sqrt{g{h}_0\beta -2g{h}_{0}z}\right)\alpha \sqrt{h_{0}g}\\ r{\left(\frac{dz}{d\tau }-\alpha \right)}^2-z\left(1+\frac{d^{2}z}{d{\tau }^2}\right)=\left(\frac{dz}{d\tau }-\alpha +\sqrt{\beta -2z}\right)\alpha \\ z\left(1+\frac{d^{2}z}{d{\tau }^2}\right)-r{\left(\frac{dz}{d\tau }-\alpha \right)}^2+\alpha \left(\frac{dz}{d\tau }+\sqrt{\beta -2z}\right)={\alpha }^2\end{array}}$

Estado estacionario

El estado estacionario se alcanza cuando

${\displaystyle \begin{array}{l}\frac{d^{2}z}{d{\tau }^2}=\mathrm{0,}\frac{dz}{d\tau }=0\\ z_{\infty }-r{\left(-\alpha \right)}^2+\alpha \sqrt{\beta -2z_{\infty }}={\alpha }^2\\ \alpha \sqrt{\beta -2z_{\infty }}=z_{\infty }-\left(1+r\right){\alpha }^2\end{array}}$

Elevando al cuadrado despejamos z_∞

${\displaystyle \begin{array}{l}{z}_{\infty }^2-2r{\alpha }^2{z}_{\infty }+\left({\left(1+r\right)}^2{\alpha }^2-\beta \right){\alpha }^2=0\\ z_{\infty }={\alpha }^2\left(r\pm \sqrt{\frac{\beta }{{\alpha }^2}-2r-1}\right)\end{array}}$

Tomamos el signo - como solución de la ecuación de segundo grado

Valor crítico del parámetro α o del flujo de entrada Q

Para que la altura de fluido se mantenga constante e igual a la inicial h₀ es decir, z_∞=1

${\displaystyle \begin{array}{l}{z}_{\infty }={\alpha }^2\left(r-\sqrt{\frac{\beta }{{\alpha }^2}-2r-1}\right)\\ r-\frac{1}{{\alpha }^2}=\sqrt{\frac{\beta }{{\alpha }^2}-2r-1}\\ r^2+\frac{1}{{\alpha }^4}-2r\frac{1}{{\alpha }^2}=\frac{\beta }{{\alpha }^2}-2r-1\\ \frac{1}{{\alpha }^4}-\left(2r+\beta \right)\frac{1}{{\alpha }^2}+{\left(r+1\right)}^2=0\\ \frac{1}{{\alpha }_c^2}=\frac{\left(2r+\beta \right)-\sqrt{{\left(2r+\beta \right)}^2-4{\left(r+1\right)}^2}}{2}\end{array}}$

Por ejemplo si r=98, lo que implica que $r=\frac{1}{2}\left(\frac{A^2}{a^2}-1\right)$, el cociente de las secciones del depósito y de orificio de salida es $\frac{A}{a}=\sqrt{197}$, o bien el cociente entre sus radios es 197^1/4=3.75. Tomando β=6, el valor crítico de α_c=1/9

Valores mayores de α_c, (lo que significa mayor flujo de entrada Q), implican que la altura final z_∞ de líquido en el depósito será mayor. Valores menores de α_c implican menores alturas finales del líquido en el depósito

Tomando β=6 y r=98, el valor de α que hace que la altura final z_∞=2.5 es

${\displaystyle \begin{array}{l}{z}_{\infty }={\alpha }^2\left(r-\sqrt{\frac{\beta }{{\alpha }^2}-2r-1}\right)\\ 2.5={\alpha }^2\left(98-\sqrt{\frac{6}{{\alpha }^2}-2·98-1}\right)\\ \frac{2.5}{{\alpha }^2}-98=\sqrt{\frac{6}{{\alpha }^2}-197}\\ {\left(\frac{2.5}{{\alpha }^2}-98\right)}^2=\frac{6}{{\alpha }^2}-197\\ \frac{6.25}{{\alpha }^4}-\frac{496}{{\alpha }^2}+9801=0\\ \frac{1}{{\alpha }^2}=\frac{496-\sqrt{991}}{2·6.25}\\ \alpha =0.1640\end{array}}$

Mayor que el valor crítico α_c=1/9

Tomando β=6 y r=98, el valor de α que hace que la altura final z_∞=0.5 es α=0.0833<1/9

Depósito vacío

Valor de α que hace que la altura final del líquido en el depósito z_∞=0, el depósito se vacíe

${\displaystyle \begin{array}{l}0={\alpha }^2\left(r-\sqrt{\frac{\beta }{{\alpha }^2}-2r-1}\right)\\ r=\sqrt{\frac{\beta }{{\alpha }^2}-2r-1}\\ \frac{\beta }{{\alpha }^2}={\left(r+1\right)}^2\\ \alpha =\frac{\sqrt{\beta }}{r+1}\end{array}}$

Por ejemplo para r=98 y β=6, α=0.0247<1/9

Por debajo de este valor de α, el depósito se vacía en un determinado tiempo

Desde el estado inicial al estado estacionario

Resolvemos la ecuación diferencial

${\displaystyle \begin{array}{l}z\left(1+\frac{d^{2}z}{d{\tau }^2}\right)-r{\left(\frac{dz}{d\tau }-\alpha \right)}^2+\alpha \left(\frac{dz}{d\tau }+\sqrt{\beta -2z}\right)={\alpha }^2\\ \frac{d^{2}z}{d{\tau }^2}=\frac{1}{z}\left\{{\alpha }^2-\alpha \left(\frac{dz}{d\tau }+\sqrt{\beta -2z}\right)+r{\left(\frac{dz}{d\tau }-\alpha \right)}^2\right\}-1\end{array}}$

con las siguientes condiciones iniciales, en el instante τ=0, z=1, dz/dτ=0

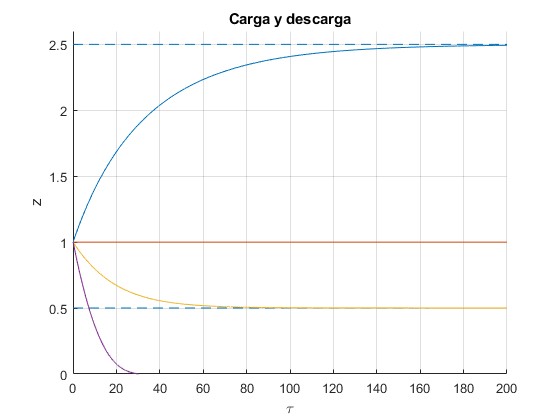
Para r=98 y β=6

• α=0.1640 (altura final z_∞=2.5)
• α=1/9 (altura final z_∞=1)
• α=0.0833 (altura final z_∞=0.5)
• α=0.02<0.0247 (se descarga en τ=30.3). Esta posibilidad no es contemplada en el modelo simple (primer apartado)

El este último caso, la función ode45 de MATLAB produce avisos (Warnings).

function carga_descarga_4
    beta=6;
    r=98;
    hold on
    opts=odeset('events',@stop_vaciado);
    for alfa=[0.1640, 1/9, 0.0833,0.02]
        f=@(t,x) [x(2); (alfa^2-alfa*(x(2)+sqrt(beta-2*x(1)))+
r*(x(2)-alfa)^2)/x(1)-1]; 
         [t,x]=ode45(f,[0,200],[1,0],opts); 
        zf=alfa^2*(r-sqrt(beta/alfa^2-2*r-1));
        line([0,200],[zf,zf],'lineStyle','--')
        plot(t,x(:,1))
    end
    ylim([0,2.6])
    hold off
    grid on
    xlabel('\tau')
    ylabel('z')
    title('Carga y descarga')

    function [value,isterminal,direction]=stop_vaciado(~,x)
        value=x(1);
        isterminal=1;    
        direction=-1; 
    end
end

Vaciado del depósito

Cuando Q=0, α=0, no hay flujo de entrada, el depósito se vacía, caso que ya se ha estudiado en la página titulada Vaciado de un depósito abierto

${\displaystyle z\frac{d^{2}z}{d{\tau }^2}-r{\left(\frac{dz}{d\tau }\right)}^2+z=0}$

Cambiamos la variable tiempo τ a desplazamiento z, obteniendo la ecuación diferencial de primer orden

${\displaystyle \begin{array}{l}V=\frac{dz}{d\tau }\\ 2\frac{dV}{d\tau }-r\frac{V^2}{z}+1=0\\ \frac{dV}{d\tau }=\frac{dV}{dz}\frac{dz}{d\tau }=V\frac{dV}{dz}=\frac{1}{2}\frac{d{V}^2}{dz}\\ \frac{1}{2}\frac{d{V}^2}{dz}-r\frac{V^2}{z}+1=0\end{array}}$

Hacemos el cambio de variable

${\displaystyle \begin{array}{l}\eta =\frac{V^2}{z},\\ \frac{d\eta }{dz}=\frac{\frac{d{V}^2}{dz}z-V^2}{z^2}=\frac{2\left(r\frac{V^2}{z}-1\right)z-V^2}{z^2}=\frac{\left(2r-1\right)V^2-2z}{z^2}\end{array}}$

• Para 2r≠1

Separando las variables, integramos

${\displaystyle \begin{array}{l}\frac{d\eta }{dz}=\frac{\left(2r-1\right)\eta -2}{z}\\ {\displaystyle \int \frac{d\eta }{\left(2r-1\right)\eta -2}={\displaystyle \int \frac{dz}{z}}}\\ \frac{1}{\left(2r-1\right)}\ln \left(\left(2r-1\right)\eta -2\right)=\ln z+c\\ \left(2r-1\right)\eta -2=c{z}^{2r-1}\\ c=-2\\ \eta =\frac{2}{2r-1}\left(1-z^{2r-1}\right)\\ V^2=\frac{2}{2r-1}\left(z-z^{2r}\right)\end{array}}$

La altura del líquido es

${\displaystyle \begin{array}{l}\frac{dz}{d\tau }=-\sqrt{\frac{2}{2r-1}}\sqrt{z-z^{2r}}\\ {\displaystyle \underset{1}{\overset{z}{\int }}\frac{dz}{\sqrt{z-z^{2r}}}}=-\sqrt{\frac{2}{2r-1}}{\displaystyle \underset{0}{\overset{\tau }{\int }}d\tau }\\ {\displaystyle \underset{1}{\overset{z}{\int }}\frac{dz}{\sqrt{z-z^{2r}}}}=-\sqrt{\frac{2}{2r-1}}\tau \end{array}}$

El tiempo de vaciado es

${\displaystyle \begin{array}{l}{\displaystyle \underset{1}{\overset{0}{\int }}\frac{dz}{\sqrt{z-z^{2r}}}}=-\sqrt{\frac{2}{2r-1}}{\rm T}\\ {\rm T}=\sqrt{\frac{2r-1}{2}}{\displaystyle \underset{0}{\overset{1}{\int }}\frac{dz}{\sqrt{z\left(1-z^{2r-1}\right)}}}\end{array}}$

Hacemos el cambio de variable

${\displaystyle \begin{array}{l}t=z^{2r-1},\sqrt{z}=t^{\frac{1}{2\left(2r-1\right)}},dt=\left(2r-1\right)z^{2r-2}dz=\left(2r-1\right)\frac{t}{t^{\frac{1}{2r-1}}}dz\\ T=\sqrt{\frac{2r-1}{2}}{\displaystyle \underset{0}{\overset{1}{\int }}\frac{t^{\frac{1}{2r-1}}}{\left(2r-1\right)t}\frac{dt}{t^{\frac{1}{2\left(2r-1\right)}}\sqrt{1-t}}}=\sqrt{\frac{1}{2\left(2r-1\right)}}{\displaystyle \underset{0}{\overset{1}{\int }}{t}^{\frac{1}{2\left(2r-1\right)}-1}{\left(1-t\right)}^{-1/2}dt}\end{array}}$

Expresamos en términos de la función beta

${\displaystyle \begin{array}{l}m=\frac{1}{4r-2}-\mathrm{1,}n=-\frac{1}{2}\\ T=\sqrt{\frac{1}{4r-2}}\frac{\Gamma \left(\frac{1}{4r-2}\right)\Gamma \left(\frac{1}{2}\right)}{\Gamma \left(\frac{1}{4r-2}+\frac{1}{2}\right)}=\sqrt{\frac{\pi }{4r-2}}\frac{\Gamma \left(\frac{1}{4r-2}\right)}{\Gamma \left(\frac{r}{2r-1}\right)}\end{array}}$

Ejemplo, para r=98, Τ=19.8

r=98;
>> sqrt(pi/(4*r-2))*gamma(1/(4*r-2))/gamma(r/(2*r-1))
ans =   19.8185

Τ es el tiempo adimensional, el tiempo real T es

${\displaystyle T=\sqrt{\frac{h_0}{g}}{\rm T}=\sqrt{\frac{\pi h_0}{g\left(4r-2\right)}}\frac{\Gamma \left(\frac{1}{4r-2}\right)}{\Gamma \left(\frac{r}{2r-1}\right)}}$

• Para 2r=1

${\displaystyle \begin{array}{l}\frac{d\eta }{dz}=-\frac{2}{z}\\ \eta =-2\ln z+c\end{array}}$

Las condiciones iniciales determinan la constante de integración c

${\displaystyle \begin{array}{l}c=0\\ \eta =-2\ln z\\ V^2=-2z\ln z\end{array}}$

La altura del líquido z

${\displaystyle \begin{array}{l}\frac{dz}{d\tau }=\sqrt{-2z\ln z}\\ {\displaystyle \underset{1}{\overset{z}{\int }}\frac{dz}{\sqrt{-z\ln z}}}=\sqrt{2}{\displaystyle \underset{0}{\overset{\tau }{\int }}d\tau }\\ {\displaystyle \underset{1}{\overset{z}{\int }}\frac{dz}{\sqrt{-2z\ln z}}}=\sqrt{2}\tau \end{array}}$

El tiempo de descarga desde z=1 a z=0, es

${\displaystyle \begin{array}{l}{\rm T}=-\frac{1}{\sqrt{2}}{\displaystyle \underset{0}{\overset{1}{\int }}\frac{dz}{\sqrt{-z\ln z}}}\\ u=\sqrt{\ln \left(\frac{1}{z}\right)},du=-\frac{dz}{2z\sqrt{\ln \left(\frac{1}{z}\right)}}=-\frac{dz}{2zu}\\ u=\sqrt{-\ln z},z=e^{-u^2}\\ {\displaystyle \int \frac{dz}{\sqrt{z\ln \left(\frac{1}{z}\right)}}=}{\displaystyle \int \frac{-2zu·du}{\sqrt{z}u}}=-2{\displaystyle \int \sqrt{z}}du=-2{\displaystyle \int e^{-u^2/2}}du\\ {\rm T}=\frac{2}{\sqrt{2}}{\displaystyle \underset{-\infty }{\overset{0}{\int }}{e}^{-u^2/2}du}\end{array}}$

Teniendo en cuenta el resultado de la integral

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-\frac{x^2}{2}\right)dx}=\sqrt{\frac{\pi }{2}}\\ {\rm T}=\sqrt{\pi }\end{array}}$

Aproximación de Torricelli

En la aproxiación de Torricelli, la velocidad de salida del líquido por el orificio es

${\displaystyle \begin{array}{l}{p}_1+\rho g{y}_1+\frac{1}{2}\rho v_1^2=p_2+\rho g{y}_2+\frac{1}{2}\rho v_2^2\\ g\left(y_1-y_2\right)=\frac{1}{2}\rho v_2^2\\ v_2=\sqrt{2gh}\end{array}}$

La ecuación diferencial se transforma en otra mucho más simple

${\displaystyle \begin{array}{l}A\frac{dh}{dt}=Q-a{v}_2\\ A\frac{dh}{dt}\approx Q-a\sqrt{2gh}\end{array}}$

Escribimos esta ecuación diferencial de forma adimensional

${\displaystyle \begin{array}{l}r=\frac{1}{2}\left(\frac{A^2}{a^2}-1\right),\alpha =\frac{Q}{A\sqrt{g{h}_0}},z=\frac{h}{h_0},\tau =t\sqrt{\frac{g}{h_0}}\\ A\frac{h_0}{\sqrt{\frac{h_0}{g}}}\frac{dz}{d\tau }=\alpha A\sqrt{g{h}_0}-a\sqrt{2g{h}_{0}z}\\ \frac{dz}{d\tau }=\alpha -\sqrt{\frac{2z}{2r+1}}\end{array}}$

Estado estacionario

${\displaystyle \begin{array}{l}0=\alpha -\sqrt{\frac{2z_{\infty }}{2r+1}}\\ z_{\infty }=\left(r+\frac{1}{2}\right){\alpha }^2\end{array}}$

Resultado ya obtenido en el primer apartado

Si z_∞=1, la altura de líquido en el depósito no cambia. El valor crítico de α_c es

${\displaystyle {\alpha }_c=\sqrt{\frac{2}{2r+1}}}$

Un valor mayor del α (o del flujo Q) implica una mayor altura z_∞ de líquido en el depósito y un α menor, implica una altura final menor

Desde el estado inicial al estado estacionario

Integrando la ecuación diferencial con la condición inicial τ=0, z=1

${\displaystyle {\displaystyle \underset{1}{\overset{z}{\int }}\frac{dz}{\alpha -k\sqrt{z}}}={\displaystyle \underset{0}{\overset{\tau }{\int }}d\tau },k=\sqrt{\frac{2}{2r+1}}}$

Para resolver la integral hacemos el cambio

${\displaystyle \begin{array}{l}t=\alpha -k\sqrt{z},\sqrt{z}=\frac{\alpha -t}{k},dt=-\frac{k}{2\sqrt{z}}dz=-\frac{k^2}{2\left(\alpha -t\right)}dz\\ {\displaystyle \int \frac{dz}{\alpha -k\sqrt{z}}=-\frac{2}{k^2}{\displaystyle \int \frac{\alpha -t}{t}dt}}=-\frac{2}{k^2}\left\{\alpha \ln t-t\right\}=-\frac{2}{k^2}\left\{\alpha \ln \left(\alpha -k\sqrt{z}\right)-\alpha +k\sqrt{z}\right\}\end{array}}$

También se puede calcular haciendo el cambio z=t²

El tiempo τ que transcurre para que el líquido alcance la altura z en el depósito

${\displaystyle \begin{array}{l}\tau =-\frac{2}{k^2}\left\{\alpha \ln \left(\alpha -k\sqrt{z}\right)-\alpha +k\sqrt{z}\right\}+\frac{2}{k^2}\left\{\alpha \ln \left(\alpha -k\right)-\alpha +k\right\}=\\ \alpha \left(2r+1\right)\ln \frac{\alpha \sqrt{2r+1}-\sqrt{2}}{\alpha \sqrt{2r+1}-\sqrt{2z}}+\left(1-\sqrt{z}\right)\sqrt{4r+2}\end{array}}$

La función implícita z(τ) se puede representar en MATLAB con fimplicit

El cociente de secciones orificio/depósito es a/A=0.3. Representamos z(τ) para tres valores de α (flujo Q)

r=(1/0.3^2-1)/2; %a/A=0.3
alfa_c=sqrt(2/(2*r+1));
hold on
for alfa=[0.6,alfa_c,0.2]
    f=@(t,z) alfa*(2*r+1)*log((alfa*sqrt(2*r+1)-sqrt(2)).
/(alfa*sqrt(2*r+1)-sqrt(2*z)))+(1-sqrt(z))*sqrt(4*r+2)-t;
    fimplicit(f,[0,30,0,2])
    zf=(r+1/2)*alfa^2;
    line([0,30],[zf,zf],'lineStyle','--')
end
hold off
grid on
xlabel('\tau')
ylabel('z')
title('Carga y descarga')

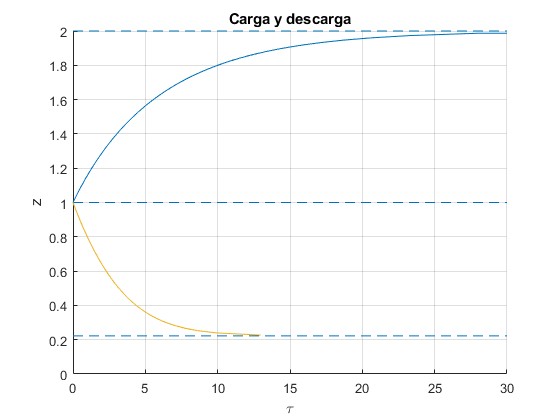
Compárese esta gráfica con la del primer apartado

Referencias

Johann Otto, Carl E Mungan. Filling and emptying a tank of liquid. Eur. J. Phys. 43 (2022) 055003 pp. 1-8

M. Blasone, F. Dell’Anno, R. De Luca, G. Torre. Mathematical model of an off-grid hybrid solar and wind power generating system. EPJ Web of Conferences 79, 01008 (2014). DOI: 10.1051/epjconf/20147901008