Vaciado de un depósito cerrado

En la figura, se muestra un depósito que tiene una altura H y una sección S₁, la sección del orificio de salida en el fondo del depósito es S₂, la altura inicial de agua es h₀ y la presión del aire en su interior p₀.

Se abre el orificio de salida del agua y se mide la altura h de la columna de agua en función del tiempo t.

Aplicamos el teorema de Bernoulli comparando dos puntos del fluido. El punto 1 en la interfase aire-agua y el punto 2 en el orificio de salida.

Sea p₁ la presión del aire en el interior del depósito, v₁ la velocidad del agua en el punto 1 y h la altura de agua en el depósito en el instante t. La presión p₂ en el orificio de salida es la atmosférica p_at y la velocidad del fluido es v₂.

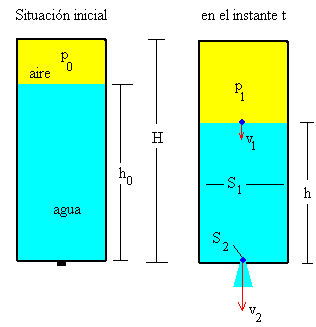
Consideramos los puntos (1) y (2) situados en la superficie libre del fluido y en el centro del orificio inferior. Las ecuaciones que describen el comportamiento de este sistema físico son:

Ecuación de continuidad

S₁·v₁=S₂·v₂

Ecuación de Bernoulli

$p_{1} + \frac{1}{2} ρ v_{1}^{2} + ρ g h = p_{a t} + \frac{1}{2} ρ v_{2}^{2}$

Expansión isotérmica del gas

p₀·S₁(H-h₀)=p₁·S₁(H-h)

Altura del fluido en equilibrio

La consecuencia más importante de estas ecuaciones es que el agua deja de salir por el orificio cuando v₂ y por tanto v₁ sean nulos.

La presión del aire en el interior del depósito será algo menor que la presión atmosférica. La diferencia será la presión correspondiente a la columna de agua de altura h.

Las ecuaciones de Bernoulli con v₁=0 y v₂=0, y la transformación isoterma

p₁+ρgh=p_atp₀ (H-h₀)=p₁·(H-h)

Obtenemos la ecuación de segundo grado en h

$ρ g h^{2} - (ρ g H + p_{a t}) h - H (p_{0} - p_{a t}) + p_{0} h_{0} = 0$

La raíz real positiva se obtiene con p₀h₀>H(p₀-p_at)

Los valores de las raíces no dependen del área de la sección del depósito S₁, ni del orificio S₂.

Ejemplo:

Sea el radio del depósito, r₁=10 cm
El radio del orificio, r₂=0.8 cm
La altura del depósito, H=50 cm
La altura inicial de agua en el depósito, h₀=40 cm
La presión inicial de aire en el depósito, p₀=4 atm

Tomando como presión atmosférica p_at=101293 Pa, la densidad del agua ρ =1000 kg/m³, resolvemos la ecuación de segundo grado en h y calculamos la altura final del agua en el depósito.

Las dos raíces son h₁=0.096 m=9.6 cm, y h₂=10.74 m que es mayor que H=0.5 m. Cuando la altura de agua en el depósito alcanza 9.6 cm deja de salir por el orificio. Calculamos la presión final del aire en el depósito

p₁=101293-1000·9.8·0.09=100411 Pa

un poco menos que la presión atmosférica

Si cambiamos la presión inicial de aire en el depósitio a p₀=6 atm

obtenemos dos raíces h₁=-0.0946 y h₂=10.9306. El depósito se vacía completamente. No se cumple que p₀h₀>H(p₀-p_at), 6·0.4<0.5·(6-1)

S1=pi*0.1^2;  %sección del depósito
S2=pi*0.008^2; %sección del orificio
H=0.5; %altura del depósito
h0=0.4; %altura inicial de agua en el depósito
pAtm=101293; %presión atmosférica
p0=4*pAtm; %presión inicial del aire en el depósito
rho=1000; %densidad del agua kg/m3
%equilibrio 
    h1=((rho*9.8*H+pAtm)-
sqrt((rho*9.8*H+pAtm)^2-4*rho*9.8*(p0*h0-H*(p0-pAtm))))/(2*rho*9.8)
    h2=((rho*9.8*H+pAtm)+
sqrt((rho*9.8*H+pAtm)^2-4*rho*9.8*(p0*h0-H*(p0-pAtm))))/(2*rho*9.8)

h1 =   0.0962
h2 =   10.7398

Variación de la altura de agua en el depósito con el tiempo

Despejamos v₁ en el sistema de tres ecuaciones

$v_{1} = \sqrt{\frac{\frac{p_{0} (H - h_{0})}{H - h} + ρ g h - p_{a t}}{\frac{1}{2} ρ (\frac{S_{1}^{2}}{S_{2}^{2}} - 1)}}$

Para hallar como cambia la altura h del agua en el depósito con el tiempo, tenemos en cuenta que,

$v_{1} = - \frac{d h}{d t}$

Integramos

$\begin{array}{l} \int_{0}^{t} d t = - \sqrt{\frac{1}{2} ρ (\frac{S_{1}^{2}}{S_{2}^{2}} - 1)} \int_{h_{0}}^{h} \frac{d h}{\sqrt{\frac{p_{0} (H - h_{0})}{H - h} + ρ g h - p_{a t}}} \\ t = - \sqrt{\frac{\frac{1}{2} ρ (\frac{S_{1}^{2}}{S_{2}^{2}} - 1) H}{p_{0} (H - h_{0})}} H \int_{h_{0} / H}^{h / H} \frac{d x}{\sqrt{\frac{1}{1 - x} + \frac{ρ g H^{2}}{p_{0} (H - h_{0})} x - \frac{p_{a t} H}{p_{0} (H - h_{0})}}} \\ t = - c \int_{h_{0} / H}^{h / H} \frac{d x}{\sqrt{\frac{1}{1 - x} + a x - b}} \end{array}$

Consideremos un depósito cerrado de 50 cm de altura y 10 cm de radio, con un orificio de 8 cm de radio. La altura inicial de agua en el depósito es de 40 cm. La presión inicial del aire en su interior es de 4 atm que vamos a ir cambiando.

Calculamos el tiempo que tarda en alcanzarse la altura de equilibrio

S1=pi*0.1^2;  %sección del depósito
S2=pi*0.008^2; %sección del orificio
H=0.5; %altura del depósito
h0=0.4; %altura inicial de agua en el depósito
pAtm=101293; %presión atmosférica
p0=4*pAtm; %presión inicial del aire en el depósito
rho=1000; %densidad del agua kg/m3
hFin=0;  %altura final del agua en el depósito
%equilibrio 
if p0*h0>H*(p0-pAtm)
    hFin=((rho*9.8*H+pAtm)-
sqrt((rho*9.8*H+pAtm)^2-4*rho*9.8*(p0*h0-H*(p0-pAtm))))/(2*rho*9.8);
end

c=-sqrt((S1^2/S2^2-1)*H*rho/(2*p0*(H-h0)))*H;
a=rho*9.8*H^2/(p0*(H-h0));
b=pAtm*H/(p0*(H-h0));

f=@(x) 1./sqrt(1./(1-x)+a*x-b);
t=c*integral(f,h0/H,hFin/H);
fprintf('La altura final es %1.3f y el tiempo %1.2f\n',hFin,t);

La altura final es 0.096 y el tiempo 6.50

Si cambiamos la presión inicial de aire en el depósitio a p₀=6 atm

La altura final es 0.000 y el tiempo 4.77

Como vemos en el código, se integra numéricamente para obtener el tiempo t

Finalmente, modificamos el script para representar la altura del fluido en función del tiempo

S1=pi*0.1^2;  %sección del depósito
S2=pi*0.008^2; %sección del orificio
H=0.5; %altura del depósito
h0=0.4; %altura inicial de agua en el depósito
pAtm=101293; %presión atmosférica
p0=4*pAtm; %presión inicial del aire en el depósito
rho=1000; %densidad del agua kg/m3
hFin=0;
%equilibrio 
if p0*h0>H*(p0-pAtm)
    hFin=((rho*9.8*H+pAtm)-sqrt((rho*9.8*H+pAtm)^2-
4*rho*9.8*(p0*h0-H*(p0-pAtm))))/(2*rho*9.8);
end

c=-sqrt((S1^2/S2^2-1)*H*rho/(2*p0*(H-h0)))*H;
a=rho*9.8*H^2/(p0*(H-h0));
b=pAtm*H/(p0*(H-h0));

f=@(x) 1./sqrt(1./(1-x)+a*x-b);
t=zeros(50,1);
h=hFin:(h0-hFin)/50:h0;
i=1;
for i=1:length(h)
    t(i)=c*integral(f,h0/H,h(i)/H);
end
plot(t,h)
grid on
xlabel('t(s)');
ylabel('x(m)');
title('Vaciado de un depósito')

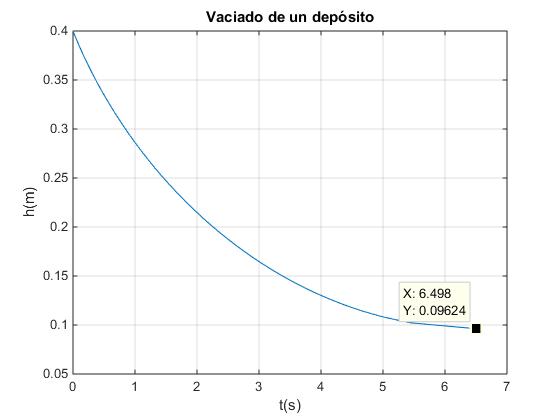
Ecuación diferencial

Resolvemos numéricamente la ecuación diferencial de primer orden

$\frac{d h}{d t} = - \sqrt{\frac{\frac{p_{0} (H - h_{0})}{H - h} + ρ g h - p_{a t}}{\frac{1}{2} ρ (\frac{S_{1}^{2}}{S_{2}^{2}} - 1)}}$

o de forma equivalente

$\begin{array}{l} \frac{d x}{d t} = - c \sqrt{\frac{1}{1 - x} + a x - b} \\ c = \sqrt{\frac{2 p_{0} (H - h_{0})}{ρ (\frac{S_{1}^{2}}{S_{2}^{2}} - 1) H^{3}}} a = \frac{ρ^{2} g H}{p_{0} (H - h_{0})} b = \frac{p_{a t} H}{p_{0} (H - h_{0})} \end{array}$

donde x=h/H, en el instante inicial t=0, x=h₀/H

El proceso de integración cesa cuando la altura final de fluido es cero o bien, si la presión no es suficiente la latura de equilibrio h₁, una de las raíces de la ecuación de segundo grado en h.

Observaremos en el código MATLAB que ya no utilizamos la rutina habitual ode45, que aquí no produce buenos resultados, sino ode15s. Búsquese en Internet el término MATLAB ode, la lista de funciones para resolver ecuaciones diferenciales.

S1=pi*0.1^2;  %sección del depósito
S2=pi*0.008^2; %sección del orificio
H=0.5; %altura del depósito
h0=0.4; %altura inicial de agua en el depósito
pAtm=101293; %presión atmosférica
p0=2*pAtm; %presión inicial del aire en el depósito
rho=1000; %densidad del agua kg/m3
hFin=0;  %altura final del agua en el depósito
%equilibrio 
if p0*h0>H*(p0-pAtm)
    hFin=((rho*9.8*H+pAtm)-sqrt((rho*9.8*H+pAtm)^2
-4*rho*9.8*(p0*h0-H*(p0-pAtm))))/(2*rho*9.8);
end

c=sqrt(2*p0*(H-h0)/((S1^2/S2^2-1)*H*rho))/H;
a=rho*9.8*H^2/(p0*(H-h0));
b=pAtm*H/(p0*(H-h0));

f=@(t,x) -c*sqrt(1/(1-x)+a*x-b); 
tspan=[0 10];
opts=odeset('events',@(t,x) vaciado_ode45(t,x,hFin/H));
[t,x]=ode15s(f,tspan,h0/H,opts);
plot(t,real(x*H));
grid on
xlabel('t(s)')
ylabel('h(cm)')
title('Vaciado de un depósito')

La función vaciado_ode45, termina el proceso de integración cuando se alcanza la altura final de equilibrio x=h_fin/H

function [value,isterminal,direction]=vaciado_ode45(~,x,xFin)
    value=x-xFin; 
    isterminal=1;
    direction=0; 
end

Cuando se eleva la presión inicial del aire en el depósito a 5 atm, el agua sale completamente del depósito, tal como se muestra en la figura

Se pueden cambiar varios parámetos: altura inicial de agua en el depósito, presión inicial del aire, la sección del orificio y ver su efecto, mediante el script de MATLAB o en la simulación más abajo.

Forma alternativa de resolver la ecuación diferencial

Definimos la función v_deposito que calcula el cuadrado de la velocidad de salida del agua del depósito por el orificio inferior

function v2 = v_deposito(t,x,p)
    r1=p(1);
    r2=p(2);
    h0=p(3)/100;
    p0=p(4);
    pAtm=101293; %en Pa 
    H=0.5;  %cm, altura depósito
    den=(r1^4/r2^4-1)*500;  %1000 es la densidad del agua
    v2=(p0*pAtm*(H-h0)/(H-x)+1000*9.8*x-pAtm)/den;
end

Definimos la función events_1que detiene el proceso de integración cuando:

la velocidad de salida del agua por el orificio inferior sea cero.
cuando la altura del agua en el depósito sea cero

function [detect,stopin,direction] = events_1(t,x,p)
    detect = [v_deposito(t,x,p) x]; 
    stopin = [1 1];  
    direction = [0 0];
end

Creamos el script

r1=10;  %radio del depósito en cm
r2=0.8; %radio del orificio en cm
h0=40; %altura inicial de agua en el depósito en cm
p0=4; %presión inicial del aire en el depósito en atm

p=[r1 r2 h0 p0];
f=@(t,x,p) -sqrt(v_deposito(t,x,p)); 
options = odeset('Events',@events_1);
[t,x,te,xe,ie] = ode15s(f, [0 20],h0/100,options,p);
plot(t,x)
ylim([0 0.5]);
grid on
xlabel('t')
ylabel('x');
title('Vaciado de un depósito cerrado')

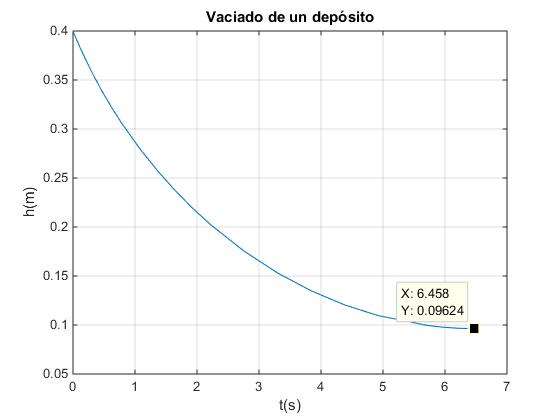
La variable te nos proporciona el tiempo hasta que se detiene el proceso de integración y xe el valor de x en dicho instante. El tiempo de vaciado del depósito y la altura del agua en el depósito son, respectivamente

te =    6.4578
xe=    0.0962

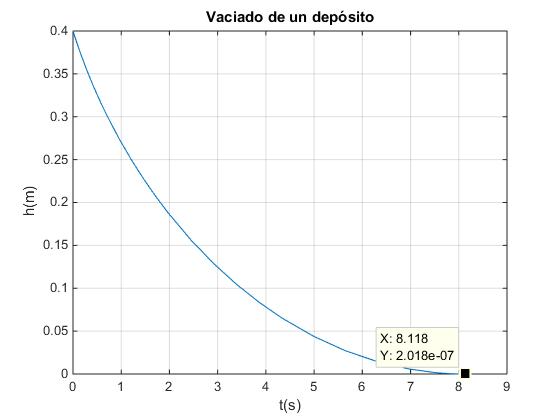
Cambiamos la presión inicial p₀=5 atm del aire en el depósito cerrado. El agua sale completamente del depósito

te =    8.1176
xe=    1.0e-06 *  0.2018 - 0.0000i

Obtenemos dos gráficas idénticas a las anteriores

Actividades

El programa interactivo estudia el comportamiento de un depósito de 50 cm de altura cerrado con un orificio en la parte inferior.

Se introduce:

el radio del depósito r₁, en el control titulado Radio depósito
el radio del orificio r₂situado en el fondo, en el control titulado Radio orificio
la presión inicial p₀ de aire (en atm) en el depósito cerrado, en el control titulado Presión aire
la altura inicial de agua en el depósito h₀ en el control titulado Altura del agua.

Se pulsa en el botón titulado Nuevo

Se representa en la parte derecha, la altura h de agua en el depósito en función del tiempo t.

El caso más importante, ocurre cuando el agua deja de salir por el orificio, se cumple que la presión del aire en el interior del depósito se hace menor que la presión atmosférica, es decir, la diferencia de presión del aire en el interior y en el exterior del depósito se hace igual a la presión que ejerce la columna de agua de altura h.

p₁-p_at=ρgh

Como hemos visto, esta altura no depende de los radios del depósito r₁ ni del orifico r₂.

En la parte superior derecha, se muestra los valores de la presión atmosférica 101 293 Pa y la presión p₁, a medida que sale el agua por el orificio inferior.

Radio depósito (cm):
Radio orificio (cm):
Presión aire (atm):
Altura del agua(cm):