Cohete propulsado por agua

El cohete consta de un recipiente de forma cilíndrica de 10 cm de radio y 50 cm de altura.

El radio del orificio situado en la parte inferior se puede modificar entre 1/2 y 1/10 del radio del recipiente. Por ejemplo, al elegir ¼, el radio del orificio es 10/4=2.5 cm

Otro dato es la proporción de agua en el recipiente. Por ejemplo, una proporción del 70% equivale a una altura de agua de 0.7·50=35 cm.

El cohete puede transportar una carga que es la suma de la carga útil más la masa de las paredes del recipiente.

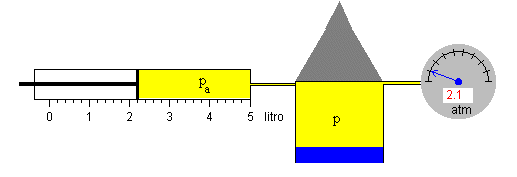
Se introduce aire comprimido en el cohete con una bomba de volumen V_b=5 litros.

Llenado de aire

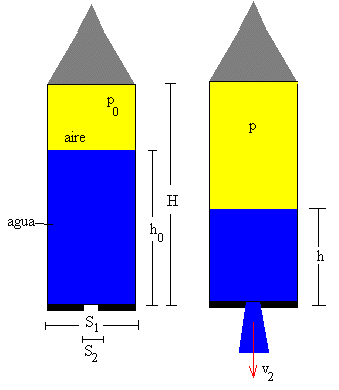
Antes de accionar la bomba tenemos n₀ moles de aire en el recipiente a la presión atmosférica y a la temperatura ambiente T.

p_at·S₁(H-h₀)=n₀RT

Cada vez que accionamos la bomba de volumen V_b, introducimos en el recipiente n moles de aire a la misma temperatura T.

p_at·V_b=nRT

Si accionamos la bomba N veces, tendremos que la presión p₀ del aire contenido en en el recipiente es

p₀·S₁(H-h₀)=(n₀+n·N)·RT

El manómetro marcará una presión final p₀ dada por la expresión

$p_{0} = p_{a t} (1 + \frac{N V_{b}}{S_{1} (H - h_{0})})$

Ejemplo:

Supongamos que el tanto por ciento de agua en el recipiente es del 70%, la altura inicial de agua es h₀=0.7·H=0.7·50=35 cm.

Sabiendo que el volumen de la bomba V_b=5 litros y el recipiente tiene un radio r₁=10 cm. Si accionamos la bomba N=4 veces, la presión del aire en el recipiente cerrado será de p₀=5.24 atm que es lo que marca el manómetro.

Empuje que experimenta el cohete

El recipiente experimenta un empuje que es el producto de la velocidad de salida del agua v_e (medida en el sistema de referencia del cohete) por la masa de agua expulsada en la unidad de tiempo dM/dt. La velocidad de salida del agua es v₂ y el volumen de agua expulsada en la unidad de tiempo (gasto) es S₂·v₂.

$E = | v_{e} \frac{d M}{d t} | = v_{2} \cdot ρ S_{2} v_{2} = ρ S_{2} v_{2}^{2}$

Como hemos visto en la página anterior el las ecuaciones que describen este sistema son:

La ecuación de Bernoulli,

p_{1} + \frac{1}{2} ρ v_{1}^{2} + ρ g h = p_{a t} + \frac{1}{2} ρ v_{2}^{2}

La ecuación de continuidad,

S₁·v₁=S₂·v₂

Expansión isotérmica del gas

p₀·S₁(H-h₀)=p₁·S₁(H-h)

que nos permiten obtener la expresión de v₁ ó v₂ en función de la altura h de agua en el recipiente.

$v_{2}^{2} = \frac{\frac{p_{0} (H - h_{0})}{H - h} + ρ g h - p_{a t}}{\frac{1}{2} ρ (1 - \frac{S_{2}^{2}}{S_{1}^{2}})}$

Variación de la altura del agua en el recipiente con el tiempo

A partir de la ecuación de continuidad, obtenemos la variación de la altura h del agua en recipiente en función del tiempo t.

$v_{1} = - \frac{d h}{d t} \frac{d h}{d t} = - \frac{S_{2}}{S_{1}} v_{2}$

Ecuaciones del movimiento

El movimiento del cohete se divide en dos etapas

Mientras sale agua por el orificio

La masa del recipiente no es constante, sino disminuye con el tiempo. La masa del recipiente es la suma de la carga útil, de la masa de las paredes del recipiente y del agua que contiene en el instante t.

m=m_u+ρS₁·h

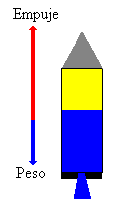
La ecuación del movimiento vertical de un cohete, es la de una partícula de masa m bajo la acción de dos fuerzas el empuje y el peso.

ma=E-mg

En forma de ecuación diferencial

$\frac{d^{2} x}{d t^{2}} = \frac{E}{m} - g$

Tenemos que resolver un sistema de dos ecuaciones diferenciales simultáneas:

Una ecuación diferencial de primer orden, que nos calcula la variación de h con el tiempo.
La ecuación del movimiento. El empuje E y la masa m del cohete son funciones de h (altura de agua en el recipiente).

$\begin{array}{l} v_{2}^{2} = f (h) = \frac{\frac{p_{0} (H - h_{0})}{H - h} + ρ g h - p_{a t}}{\frac{1}{2} ρ (1 - \frac{S_{2}^{2}}{S_{1}^{2}})} \\ \frac{d h}{d t} = - \frac{S_{2}}{S_{1}} \sqrt{f (h)} \\ \frac{d^{2} x}{d t^{2}} = \frac{ρ S_{2}}{ρ S_{1} h + m_{u}} f (h) - g \end{array}$

En el programa interactivo, se ha resuelto el sistema de dos ecuaciones diferenciales por el método de Runge-Kutta, sin realizar ninguna aproximación. Lo que nos permite incluso examinar el caso de que la presión del aire en el interior del recipiente no sea suficiente para expulsar todo el agua y se alcance una altura del fluido en equilibrio, tal como vimos en la página anterior.

Cuando se ha agotado el agua

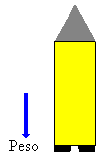
Una vez que se ha agotado el agua del depósito, el aire en el interior del depósito tiene una presión p mayor que la presión atmosférica, pero supondremos despreciable el impulso adicional proporcionado por la salida del aire por el orificio inferior hasta que se igualan las presiones en el interior y exterior del recipiente. Sobre el cohete actúa solamente el peso, por lo que el movimiento es uniformemente acelerado

$\begin{array}{l} a = - g \\ v = v_{0} - g (t - t_{0}) \\ x = x_{0} + v_{0} (t - t_{0}) - \frac{1}{2} g {(t - t_{0})}^{2} \end{array}$

donde x₀, y v₀ son la posición y la velocidad del móvil en el instante t₀ en el que se ha agotado el combustible, en este caso, agua.

El rozamiento del aire

Al moverse un cuerpo en el aire con velocidad v, experimenta una fuerza de rozamiento, que es proporcional al cuadrado de la velocidad

Esta fuerza de rozamiento no es importante durante la fase de lanzamiento que dura poco tiempo y durante la cual predomina la fuerza de empuje, pero puede ser importante en la fase de vuelo libre desde que se agota el combustible hasta que alcanza la máxima altura.

La fuerza de rozamiento no se ha tenido en cuenta en la simulación del cohete propulsado por agua.

Resultados

En este apartado vamos a examinar la dinámica del cohete de 10 cm de radio, que transporta una carga útil de 5 kg, el orificio de salida del agua es de 10/6 cm y la proporción de agua en el depósito es del 70%. Mientras el agua sale por el orificio, hay que resolver numéricamente un sistema de dos ecuaciones diferenciales, o tes ecuaciones diferenciales de primer orden. Representamos la velocidad del cohete y su altura sobre el suelo, para dos presiones iniciales de aire distintas: 3 atm y 5 atm. En el primer caso, la presión no es suficiente para que salga todo el agua y en el segundo, sale completamente expulsada del depósito del cohete.

S1=pi*0.1^2;  %sección del depósito
S2=pi*(0.1/6)^2; %sección del orificio
H=0.5; %altura del depósito
h0=0.7*0.5; %altura inicial de agua en el depósito (70%)
pAtm=101293; %presión atmosférica
p0=3*pAtm; %presión inicial del aire en el depósito
rho=1000; %densidad del agua kg/m3
mu=5; %carga útil que transporta

c=2*p0*(H-h0)/((1-S2^2/S1^2)*rho);
a=rho*9.8/(p0*(H-h0));
b=pAtm/(p0*(H-h0));
f=@(h) c*(1./(H-h)+a*h-b); 

if(rho*S2*f(h0)/(rho*S1*h0+mu)<9.8)
    disp('No despega, el empuje es menor que el peso')
    return;
end

hFin=0;  %altura final del agua en el depósito
if p0*h0>H*(p0-pAtm)
    hFin=((rho*9.8*H+pAtm)-sqrt((rho*9.8*H+pAtm)^2-
4*rho*9.8*(p0*h0-H*(p0-pAtm))))/(2*rho*9.8);
end
%x(1) es la altura de agua en el depósito, x(2) la posición del cohete y
%x(3)su velocidad
x0=[h0,0,0];
fg=@(t,x) [-S2*sqrt(f(x(1)))/S1; x(3); rho*S2*f(x(1))/(rho*S1*x(1)+mu)-9.8];
tspan=[0 100];
opts=odeset('events',@(t,x) vaciado_cohete(t,x,hFin));
[t,x]=ode15s(fg,tspan,x0,opts);
subplot(2,1,1)
plot(t,x(:,2))
grid on
xlabel('t(s)')
ylabel('x(m)')
subplot(2,1,2)
plot(t,x(:,3))
grid on
xlabel('t(s)')
ylabel('v(m/s)')

function [value,isterminal,direction]=vaciado_cohete(~,x,hFin)
    value=[x(1)-hFin, x(2), x(3)]; 
    isterminal=[1,1,0];
    direction=0; 
end

Con una presión de 3 atm, el cohete acelera, el empuje es mayor que el peso, la velocidad alcanza un máximo cuando el empuje se iguala al peso y disminuye cuando el empuje es menor que el peso. El cohete regresa al suelo antes de que termine de salir el agua por el orificio.

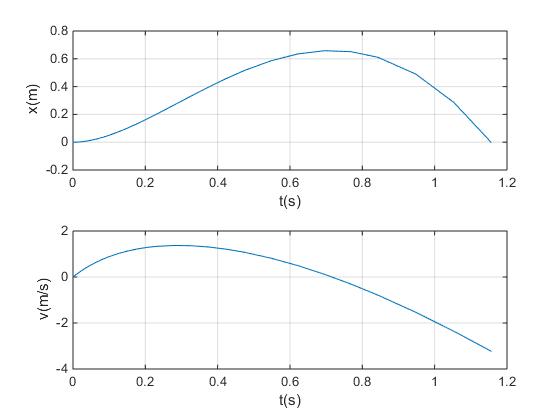
Con una presión de 5 atm, el cohete acelera, el empuje es siempre mayor que el peso, la velocidad se incrementa

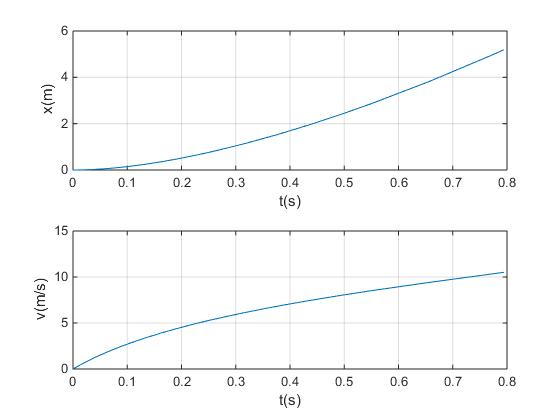
Con el siguiente script investigamos la proporción óptima de agua en el depósito para una presión de 5 atm, una carga útil de 5 kg y un orificio de radio 10/6 cm. Vemos que la proporción óptima es del 46%

S1=pi*0.1^2;  %sección del depósito
S2=pi*(0.1/6)^2; %sección del orificio
H=0.5; %altura del depósito
h0=0.7*0.5; %altura inicial de agua en el depósito (70%)
pAtm=101293; %presión atmosférica
p0=5*pAtm; %presión inicial del aire en el depósito
rho=1000; %densidad del agua kg/m3
hFin=0;  %altura final del agua en el depósito
mu=5; %carga útil que transporta

i=0;
vMax=zeros(0,81);
hAgua=zeros(0,81);
for percent=0.1:0.01:0.9
    i=i+1;
    h0=percent*H;
    c=2*p0*(H-h0)/((1-S2^2/S1^2)*rho);
    a=rho*9.8/(p0*(H-h0));
    b=pAtm/(p0*(H-h0));

    f=@(h) c*(1./(H-h)+a*h-b); 

    if(rho*S2*f(h0)/(rho*S1*h0+mu)<9.8)
        disp('No despega, el empuje es menor que el peso')
        hAgua(i)=percent*100;
        vMax(i)=0;
        continue;
    end

    if p0*h0>H*(p0-pAtm)
        hFin=((rho*9.8*H+pAtm)-sqrt((rho*9.8*H+pAtm)^2
-4*rho*9.8*(p0*h0-H*(p0-pAtm))))/(2*rho*9.8);
    end

    x0=[h0,0,0];
    fg=@(t,x) [-S2*sqrt(f(x(1)))/S1; x(3); rho*S2*f(x(1))
/(rho*S1*x(1)+mu)-9.8];
    tspan=[0 100];
    opts=odeset('events',@(t,x) vaciado_cohete(t,x,hFin));
    [t,x]=ode15s(fg,tspan,x0,opts);
    hAgua(i)=percent*100;
    vMax(i)=x(end,3);
end
plot(hAgua,vMax);
grid on
xlabel('f(%)')
ylabel('v_m(m/2)')
title('Cohete de agua')

>> [xmax nmax]=max(vMax);
>> xmax
xmax =   16.2649
>> hAgua(nmax)
ans =    46

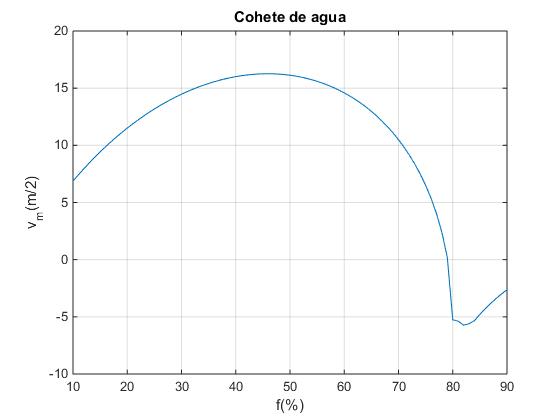
Con un orificio un poco mayor de radio 10/4 de cm, mejoramos la velocidad final del cohete con una proporción del 50% de agua en el depósito

>> [xmax nmax]=max(vMax);
>> vMax(nmax)
ans =   18.4223
>> hAgua(nmax)
ans =    50

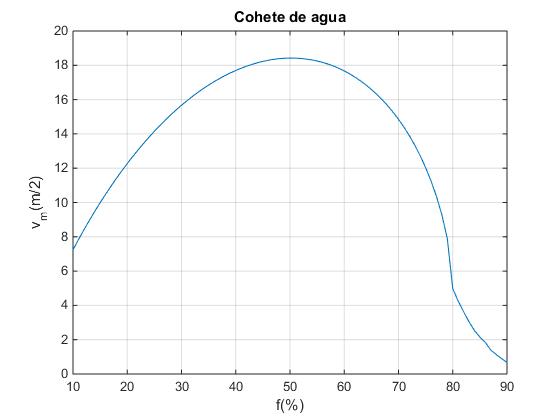
Probaremos el efecto de los distintos parámetros, modificando sus valores

Actividades

Se introduce

La proporción de agua en el recipiente, en el control titulado % de agua
El radio del orificio de salida del agua, eligiendo una fracción del radio del depósito, en el control titulado Radio orificio.
La carga que transporta el cohete (que incluye la carga útil y las paredes del recipiente) introduciendo un valor en el control titulado Carga.

Se pulsa el botón titulado Nuevo

A continuación, se pulsa varias veces en el botón titulado Aire, para introducir aire en el interior del recipiente. En el manómetro situado a la derecha del cohete vemos como va aumentando la presión.

Se pulsa el botón titulado ►.

Veremos que el agua es expulsada por el orificio inferior, el aire se expande en el interior del recipiente disminuyendo la presión.

Dos flechas indican las magnitudes relativas del peso y del empuje durante la fase de lanzamiento. Cuando se se termina de salir el agua, el empuje se hace cero y el cohete se mueve con movimiento uniformemente acelerado hasta que alcanza la altura máxima.

En la parte izquierda, un punto de color rojo indica la posición (altura) del cohete.

Los datos del tiempo, velocidad y posición que aparecen en color rojo, corresponden al instante en el que deja de salir agua por el orificio y por tanto, el empuje es nulo. El cohete alcanza la máxima velocidad, continúa su movimiento ascendente hasta que su velocidad se hace cero, alcanzando en ese instante la máxima altura.

Radio orificio: % agua:
Carga (kg):

Referencias

Finney G.A., Analysis of water-propelled rocket: A problem in honors physics. Am. J. Phys. 68 (3) March 2000, pp. 223-227.