El tubo en forma de U tiene los extremos abiertos.

Consideremos un líquido de densidad ρ contenido en un tubo en forma de U de sección uniforme S. La longitud del líquido es l y su volumen S·l. En la situación de equilibrio la altura del líquido en ambas brazos verticales es el misma. Supongamos que por algún procedimiento, se desnivela el líquido en las dos brazos.

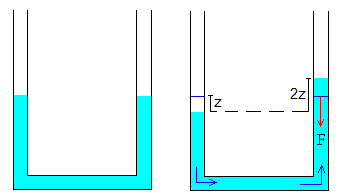
Si consideramos el líquido como un fluido ideal, libre de rozamiento con las paredes del recipiente que lo contiene, el líquido empezará a oscilar con un periodo que depende únicamente de la longitud l de de la columna de líquido.

Cuando el líquido se desplaza z hacia la derecha, el desnivel entre las dos brazos del tubo en forma de U es 2z, tal como se aprecia en la figura. La fuerza F que se opone al movimiento de todo el fluido, es el peso de la columna de fluido de sección S y altura 2z.

• La masa de todo el fluido es ρSl
• La fuerza F tiene por módulo, ρS(2z)g, es de sentido contrario al desplazamiento z.

La ecuación del movimiento se escribe (masa por aceleración igual a fuerza)

${\displaystyle \rho Sl\frac{d^{2}z}{d{t}^2}=-\rho S(2z)g\frac{d^{2}z}{d{t}^2}+\frac{2g}{l}z=0}$

Se trata de la ecuación diferencial de un MAS cuya frecuencia angular es ω²=2g/l o cuyo periodo es

${\displaystyle P=2\pi \sqrt{\frac{l}{2g}}}$

La solución de la ecuación diferencial es

z=Acos(ωt)+Bsin(ωt).

La velocidad de la columna de líquido en el instante t es

v=dz/dt=-Aωsin(ωt)+Bωcos(ωt).

donde A y B se determinan a partir de las condiciones iniciales.

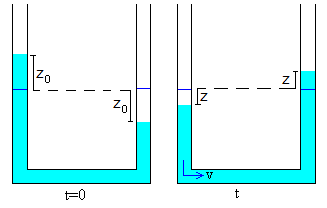
Para conseguir un desnivel inicial entre los brazos verticales del tubo, se pone un corcho en el extremo de un brazo, se extrae algo de aire, el líquido en este brazo se eleva z₀ y desciende la misma longitud en el otro brazo. Se descorcha el tubo y se empieza a contar el tiempo, en el instante inicial t=0, tenemos z=z₀ y v=0.

Con estas condiciones iniciales, z=z₀cos(ωt), v=-ωz₀sin(ωt)

Balance energético

Para efectuar el balance energético, comparamos la situación inicial en el instante t=0 y la situación final en el instante t, tal como se muestra en la figura

En el instante t, cuando la columna de líquido de longitud l y sección S lleva una velocidad v, la energía cinética es

${\displaystyle E_k=\frac{1}{2}(\rho Sl)v^2=\frac{1}{2}(\rho Sl)z_0^2{\omega }^2{\sin }^2(\omega t)=\rho Sg·z_0^2{\sin }^2(\omega t)}$

Comparamos la energía potencial en la situación de equilibrio con la energía potencial cuando el desnivel del líquido en las dos brazos es 2z.

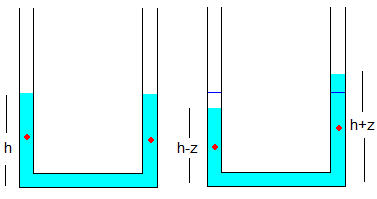
El líquido contenido en el tubo horizontal no cambia su energía potencial. Los centros de masas de las columnas verticales de fluido se han marcado mediante un punto de color rojo, cuya altura es la mitad de la longitud de dicha columna.

• En la situación de equilibrio, la energía potencial, referida al suelo, vale

ρSh·g·h/2+ρSh·g·h/2=ρS·g·h²

• En el instante t, el desnivel del líquido en los dos brazos es 2z, la energía potencial referida al suelo es.

ρS(h-z)·g·(h-z)/2+ ρS(h+z)·g·(h+z)/2=ρS·g·(h²+z²)

La energía potencial con respecto a la situación de equilibrio, es la diferencia entre ambas cantidades.

${\displaystyle E_p=\rho Sg{z}^2=\rho Sg{z}_0^2{\cos }^2(\omega t)}$

La suma de la energía potencial y de la energía cinética es constante e igual a la energía potencial en la situación inicial, t=0, z=z₀, v=0

${\displaystyle E=E_k+E_p=\rho Sg{z}_0^2}$

El tubo en forma de U está cerrado por uno de sus extremos

Consideremos un tubo en forma de U con uno de sus extremos taponado con un corcho. Inicialmente, la altura del aire encerrado entre la superficie del líquido y el tapón es H y está a la presión atmosférica p₀.

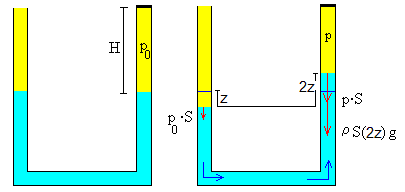
Cuando el fluido se desplaza z de la posición de equilibrio, hacia la derecha, actúan tres fuerzas sobre todo el líquido (ρSl) contenido en el tubo en forma de U.

• El peso de la columna de líquido de altura 2z, opuesta al desplzamiento del líquido

• La fuerza que ejerce la presión del aire comprimido sobre la superficie libre del líquido en el brazo derecho, opuesta al movimiento del fluido

• La fuerza que ejerce la presión de aire exterior sobre la superficie libre del líquido en el brazo izquierdo, favoreciendo el movimiento.

La fuerza neta que se opone al movimiento del todo el líquido del tubo es

-ρS(2z)g-pS+p₀·S

En el apartado anterior, al estar abiertas los dos brazos del tubo, p coincide con p₀, por lo que las fuerzas que ejercía el aire sobre las dos superficies libres del líquido se cancelaba.

Si suponemos que las oscilaciones son rápidas, el aire encerrado entre el líquido y el tapón, experimenta una transformación aproximadamente adiabática.

${\displaystyle p_0{(SH)}^{\gamma }=p{(S(H-z))}^{\gamma }}$

Supondremos también que la amplitud de las oscilaciones son pequeñas respecto de la longitud de la columna de aire, H, por lo que z<<H.

${\displaystyle p=p_0{\left(1-\frac{z}{H}\right)}^{-\gamma }\approx p_0\left(1+\gamma \frac{z}{H}\right)}$

La ecuación del movimiento del líquido contenido en el tubo en forma de U será

${\displaystyle \begin{array}{l}(\rho Sl)\frac{d^{2}z}{d{t}^2}=-\rho S(2z)g-p_{0}S\gamma \frac{z}{H}\\ \frac{d^{2}z}{d{t}^2}+\left(\frac{2g}{l}+\frac{\gamma p_0}{\rho Hl}\right)z=0\end{array}}$

El líquido contenido en el tubo, describe un M.A.S. cuyo periodo es

${\displaystyle P=2\pi \sqrt{\frac{l}{2g+\gamma \frac{p_0}{\rho H}}}}$

Si elegimos como condiciones iniciales t=0, x=0, y v=v₀. La solución de la ecuación diferencial es

z=(v₀/ω)sin(ωt)
v=dz/dt=v₀cos(ωt)

Balance energético

Para efectuar el balance energético, comparamos la situación inicial en el instante t=0 y la situación final en el instante t, tal como se muestra en la figura

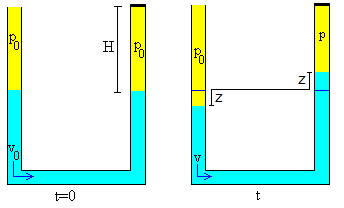
En la situación inicial t=0, la energía es cinética

${\displaystyle E_k=\frac{1}{2}(\rho Sl)v_0^2}$

La energía potencial respecto de la situación de equilibrio es cero

E_p=0

En el instante t, cuando la columna de líquido de longitud l y sección S lleva una velocidad v, la energía cinética es

${\displaystyle E_k=\frac{1}{2}(\rho Sl)v_0^2{\cos }^2(\omega t)}$

La expresión de la energía potencial con respecto a la situación de equilibrio es la misma que la que se dedujo en el apartado anterior.

${\displaystyle E_p=\rho Sg{z}^2=\rho Sg\frac{v_0^2}{{\omega }^2}{\sin }^2(\omega t)}$

La suma de la energía cinética y de la energía potencial no es una cantidad constante, ya que hemos de considerar el trabajo realizado por las fuerzas exteriores (el aire que rodea a la columna de líquido). El aire encerrado en el brazo derecho se comprime adiabáticamente y el aire exterior se expande a presión constante durante media oscilación y durante la otra media, el aire encerrado se expande y el aire de la atmósfera que rodea al dispositivo se comprime.

La variación de energía, es la energía final menos la inicial

${\displaystyle \begin{array}{l}\Delta E=E_f-E_i=\frac{1}{2}\rho Sl{v}_0^2{\text{cos}}^2(\omega t)+\rho Sg\frac{v_0^2}{{\omega }^2}{\sin }^2(\omega t)-\frac{1}{2}\rho Sl{v}_0^2=\\ =\rho S{v}_0^2\left(-\frac{1}{2}l+\frac{g}{{\omega }^2}\right){\sin }^2(\omega t)=-\gamma \frac{p_{0}S}{2H}\frac{v_0^2}{{\omega }^2}{\sin }^2(\omega t)\end{array}}$

La diferencia entre la energía final E_f y la energía inicial E_i, es el trabajo de las fuerzas exteriores W_ext, como vamos a comprobar más abajo.

Trabajo realizado por las fuerzas exteriores

Consideremos la situación que se muestra en la figura.

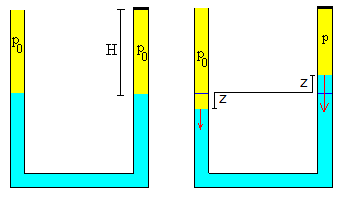
La atmósfera que rodea al dispositivo y que actúa sobre la superficie libre del brazo izquierdo, realiza un trabajo que es el producto de la presión constante p₀ por el incremento de volumen (S·z).

W₁=p₀(S·z)

El aire encerrado en el brazo derecho se comprime adiabáticamente, por lo que el trabajo realizado es

${\displaystyle W_2=-{\displaystyle \underset{0}{\overset{z}{\int }}pSdz}\approx -{\displaystyle \underset{0}{\overset{z}{\int }}{p}_0\left(1+\gamma \frac{z}{H}\right)Sdz}=-p_{0}Sz-\gamma \frac{p_{0}S}{2H}{z}^2}$

Se ha tenido en cuenta, la relación existente entre p y p₀ en la aproximación de que z<<H, deducida al principio de este apartado

La suma de ambas contribuciones es el trabajo realizado por las fuerzas exteriores

${\displaystyle W_{ext}=W_1+W_2=-\gamma \frac{p_{0}S}{2H}{z}^2=-\gamma \frac{p_{0}S}{2H}\frac{v_0^2}{{\omega }^2}{\sin }^2(\omega t)}$

El trabajo de las fuerzas exteriores modifica la energía del sistema de partículas, es decir, es igual a la diferencia entre la energía final y la inicial del sistema. Ya empleamos esta fórmula para deducir la ecuación de Bernoulli.

Como hemos comprobado, el trabajo realizado por el aire que rodea a la columna de líquido es igual a la diferencia entre la energía final E_f y la energía inicial E_i.

Medida del índice adiabático del aire

Si llamamos P₁ al periodo de las oscilaciones del líquido con las dos brazos abiertas y P₂ el periodo de las oscilaciones del mismo líquido con un tubo taponado en uno de sus extremos. La relación entre los cuadrados de los periodos es

${\displaystyle \frac{P_1^2}{P_2^2}=\frac{2g+\frac{\gamma p_0}{\rho H}}{2g}}$

 Despejando el índice adiabático γ de aire

${\displaystyle \gamma =\frac{2g\rho H}{p_0}\left(\frac{P_1^2}{P_2^2}-1\right)}$

Si el líquido contenido en el tubo en forma de U es mercurio, la presión atmosférica es p₀=ρgH₀, siendo H₀=0.76 m, la altura de la columna de mercurio en el experimento de Torricelli. La fórmula final que nos permite calcular el índice adiabático γ es

${\displaystyle \gamma =\frac{2H}{H_0}\left(\frac{P_1^2}{P_2^2}-1\right)}$

En la experiencia de laboratorio, descrita en el artículo citado en las referencias, los datos son los siguientes:

• Se emplea mercurio como líquido, que se introduce un un tubo de Pyrex de 19 mm.

• La longitud de la columna de líquido es de l=75 cm.

• La columna de aire entre la superficie libre y el tapón que cierra uno de los extremos del tubo en U  tiene una longitud H=84 cm.

• La presión atmosférica p₀ corresponde a la altura de una columna de mercurio de H₀=75.4 cm.

El valor obtenido para el índice adiabático de aire fue γ=1.38

Actividades

La longitud de la parte horizontal del tubo en U es de 20 cm

Establecemos la altura inicial de fluido en el tubo en U, en el control Altura fluido

Activamos el botón de radio titulado extremos abiertos

Se pulsa el botón titulado Nuevo

Medimos el periodo P₁ de las oscilaciones de la columna de líquido con los extremos del tubo en forma de U abiertos.

Activamos el botón de radio titulado extremo cerrado. Observamos en el brazo derecho una columna de aire que se va a comprimir y expandir adiabáticamente.

Medimos el periodo P₂ de las oscilaciones. El dato que necesitamos es la presión atmosférica que es la presión que ejerce una columna de mercurio de H₀=0.76 m

En la parte derecha, se representa el MAS que describe la superficie libre del líquido, la altura x del líquido en función del tiempo t, medida respecto de la situación de equilibrio estable, es decir, cuando el líquido en ambas brazos está a la misma altura. Arbitrariamente, se ha asignado una amplitud de 0.05=5 cm, para que se cumpla en todos los casos, que el desplazamiento x es siempre pequeño respecto de la altura H de la columna de aire.

En la parte inferior derecha, una barra horizontal nos muestra las energías que intervienen.

Cuando los extremos del tubo están abiertos, la suma de la energía cinética y potencial se mantiene constante. La energía cinética se transforma en potencial y viceversa, tal como ocurre en un sistema formado por una partícula unida a un muelle elástico, o en un péndulo simple.

Cuando un extremo del tubo está cerrado, la suma de la energía cinética y potencial no es constante, ya que hay que tener en cuenta el trabajo de las fuerzas exteriores (del aire), este trabajo es igual a la diferencia entre la energía final y la energía inicial. 

Ejemplo:

Establecemos la altura inicial de fluido en 0.40 m.

Medimos el periodo de las oscilaciones con los extremos abiertos del tubo en forma de U,  P₁=1.42 s.

Activamos el botón de radio titulado extremo cerrado, que equivale a colocar un tapón en el extremo derecho del tubo en U. La longitud de la columna de aire encerrado en el brazo derecho es H=0.6

Medimos el periodo de las oscilaciones P₂=1.03

Con estos dos datos obtenemos el índice adiabático γ del aire, aplicando la fórmula deducida en el apartado anterior

${\displaystyle \gamma =\frac{2·0.6}{0.76}\left(\frac{{1.42}_1^2}{{1.03}^2}-1\right)=1.42}$

Comprobación:

La longitud de la columna de mercurio es L=2·0.4+0.2=1.0 m, ya que la longitud de la parte horizontal del tubo en U mide 20 cm.

El periodo de las oscilaciones del líquido con los extremos abiertos es:

${\displaystyle P_1=2\pi \sqrt{\frac{1.0}{2·9.8}}=1.42\text{s}}$

La longitud de la columna de aire encerrado en el brazo derecho del tubo es H=1.0-0.4=0.6 m

Sabiendo que el índice adiabático del aire es γ=1.4, y que la presión atmosférica equivale a la presión que ejerce una columna de mercurio de H₀=0.76 m de altura, se simplifica la densidad ρ del mercurio en la fórmula que calcula el periodo P₂.

${\displaystyle P_2=2\pi \sqrt{\frac{1.0}{2·9.8+1.4\frac{9.8·0.76}{0.6}}}=1.03\text{s}}$

Los periodos calculados coinciden con los tiempos P₁ y P₂ medidos.

Referencias

Del apartado,"Medida del índice adiabático del aire"

Kofsky, I. A Sophomore laboratory experiment on determining γ for air Am. J. Phys. 17 (1949) pp. 430-431