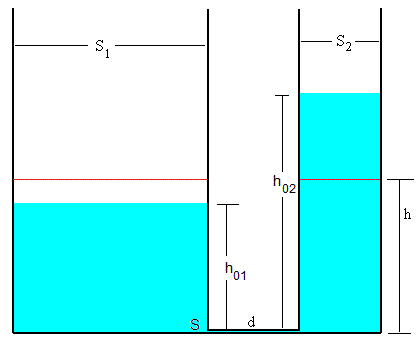
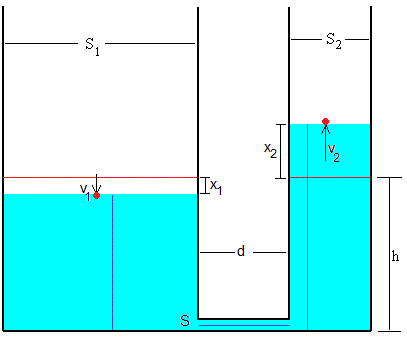
Consideremos dos recipientes de sección S₁ y S₂, comunicados por su parte inferior a través de un tubo de longitud d y pequeña sección S. Se cierra la llave de paso del tubo horizontal y se vierte un líquido en los recipientes hasta una altura h₀₁ y h₀₂ tal como se muestra en la figura

Cuando se abre la llave de paso y se comunican los dos recipientes, el líquido fluye a través del tubo desde un recipiente al otro, hasta que al cabo de un tiempo se alcanza una altura de equilibrio h

Como el volumen total de líquido no ha cambiado, desde la situación inicial a la de equilibrio, tendemos que

S₁h₀₁+S₂h₀₂=S₁h+S₂h

En esta página, se considera que el líquido que se vierte en los recipientes es ideal, el estado de equilibrio no se alcanza. El líquido pasa de un recipiente hacia el otro y vicersa, oscilando entre alturas constantes, h₀₂ y 2h-h₀₂ en el recipiente de la derecha.

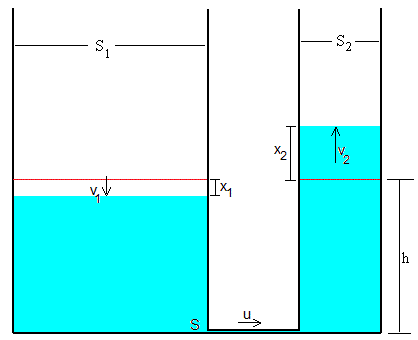
En un instante dado t, el nivel del líquido por debajo de la altura de equilibrio en el primer vaso es x₁ y en el segundo, el nivel está por encima x₂. Como el volumen de líquido no ha cambiado

S₁x₁=S₂x₂

Si v₁ es la velocidad del fluido en el primer recipiente, v₂ en el segundo y u en el tubo que comunica ambos recipientes. Se cumplirá por la ecuación de continuidad que

S₁v₁=S₂v₂=Su

Energías

• La energía cinética del líquido contenido en el recipiente de la izquierda es

${\displaystyle E_{k1}=\frac{1}{2}\left(\rho S_1(h-x_1)\right)v_1^2=\frac{1}{2}\left(\rho S_1\left(h-\frac{S_2}{S_1}{x}_2\right)\right){\left(\frac{S_2}{S_1}{v}_2\right)}^2}$

• La energía cinética del líquido contenido en el recipiente de la derecha es

${\displaystyle E_{k2}=\frac{1}{2}\left(\rho S_2(h+x_2)\right)v_2^2}$

• La energía cinética del líquido contenido en tubo horizontal que comunica los recipientes es

${\displaystyle E_{k3}=\frac{1}{2}\left(\rho Sd\right)u^2=\frac{1}{2}\left(\rho Sd\right){\left(\frac{S_2}{S}{v}_2\right)}^2}$

La energía cinética total es

${\displaystyle E_k=\frac{1}{2}\rho S_2\left\{\left(1+\frac{S_2}{S_1}\right)h+\left(1-\frac{S_2^2}{S_1^2}\right)x_2+\frac{S_2}{S}d\right\}{v}_2^2}$

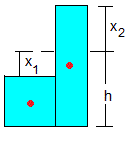
La posición del centro de masas del recipiente izquierdo y derecho, se señalan por un punto de color rojo en la figura. La posición del centro de masas del líquido contenido en los dos recipientes es

${\displaystyle x_c=\frac{S_1(h-x_1)\left(\frac{h-x_1}{2}\right)+S_2(h+x_2)\left(\frac{h+x_2}{2}\right)}{S_1(h-x_1)+S_2(h+x_2)}=\frac{1}{2}\left(h+\frac{S_2}{S_1}\frac{x_2^2}{h}\right)}$

La energía potencial del centro de masas es

${\displaystyle E_p=\rho \left(S_1+S_2\right)h·g·x_c=\frac{1}{2}\rho \left(S_1+S_2\right)g\left(h^2+\frac{S_2}{S_1}{x}_2^2\right)}$

Ecuación del movimiento

La lagrangiana L=E_k-E_p es

${\displaystyle L=\frac{1}{2}\rho S_2\left\{\left(1+\frac{S_2}{S_1}\right)h+\left(1-\frac{S_2^2}{S_1^2}\right)x_2+\frac{S_2}{S}d\right\}{\left(\frac{d{x}_2}{dt}\right)}^2-\frac{1}{2}\rho S_2\left(1+\frac{S_1}{S_2}\right)g\left(h^2+\frac{S_2}{S_1}{x}_2^2\right)}$

Para simplificar la notación, denominaremos y=x₂. La ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{y}}\right)-\frac{\partial L}{\partial y}=0\\ \frac{d}{dt}\left(2\left\{\left(1+\frac{S_2}{S_1}\right)h+\left(1-\frac{S_2^2}{S_1^2}\right)y+\frac{S_2}{S}d\right\}\frac{dy}{dt}\right)-\left(1-\frac{S_2^2}{S_1^2}\right){\left(\frac{dy}{dt}\right)}^2+2\left(1+\frac{S_1}{S_2}\right)g\frac{S_2}{S_1}y=0\\ 2\left\{\left(1+\frac{S_2}{S_1}\right)h+\left(1-\frac{S_2^2}{S_1^2}\right)y+\frac{S_2}{S}d\right\}\frac{d^{2}y}{d{t}^2}+\left(1-\frac{S_2^2}{S_1^2}\right){\left(\frac{dy}{dt}\right)}^2+2\left(1+\frac{S_2}{S_1}\right)gy=0\\ \left\{h+\frac{S_1{S}_2}{S\left(S_1+S_2\right)}d+\left(1-\frac{S_2}{S_1}\right)y\right\}\frac{d^{2}y}{d{t}^2}+\frac{1}{2}\left(1-\frac{S_2}{S_1}\right){\left(\frac{dy}{dt}\right)}^2+gy=0\\ (A+By)\frac{d^{2}y}{d{t}^2}+\frac{1}{2}B{\left(\frac{dy}{dt}\right)}^2+gy=0\end{array}}$

Resolveremos la ecuación del movimiento por procedimientos numéricos con la siguientes condiciones iniciales: en el instante t=0, la altura del fluido en el recipiente de la derecha por encima de la de equilibrio es y₀=x₀₂=h₀₂-h (véase la primera figura). La velocidad inicial del líquido en los recipientes es cero, dy/dt=0

Oscilaciones armónicas

Cuando las secciones de los recipientes son iguales, S₁=S₂. La ecuación del movimiento es

${\displaystyle \left\{h+\frac{S_2}{2S}d\right\}\frac{d^{2}y}{d{t}^2}+gy=0}$

Se trata de la ecuación diferencial de las oscilaciones libres de frecuencia angular ω₀ y periodo P=2π/ω₀

${\displaystyle {\omega }_0^2=\frac{g}{h+\frac{S_2}{2S}d}}$

Energía

Hemos calculado, la energía cinética y potencial del sistema formado por los dos recipientes y el tubo horizontal que los comunica

La energía inicial es solamente potencial

${\displaystyle E_0=\frac{1}{2}\rho S_2\left(1+\frac{S_1}{S_2}\right)g\left(h^2+\frac{S_2}{S_1}{x}_{02}^2\right)}$

La energía en el instante t es

${\displaystyle E=\frac{1}{2}\rho S_2\left\{\left(1+\frac{S_2}{S_1}\right)h+\left(1-\frac{S_2^2}{S_1^2}\right)x_2+\frac{S_2}{S}d\right\}{v}_2^2+\frac{1}{2}\rho S_2\left(1+\frac{S_1}{S_2}\right)g\left(h^2+\frac{S_2}{S_1}{x}_2^2\right)}$

Si el líquido es ideal, la energía se mantiene constante

${\displaystyle \begin{array}{l}\left\{h+\frac{S_1{S}_2}{S\left(S_1+S_2\right)}d+\left(1-\frac{S_2}{S_1}\right)x_2\right\}{v}_2^2=g\left(x_{02}^2-x_2^2\right)\\ \left(A+By\right){\left(\frac{dy}{dt}\right)}^2=g\left(y_0^2-y^2\right)\end{array}}$

Periodo

Despejamos dt e integramos

${\displaystyle \begin{array}{l}dt=\sqrt{\frac{A+By}{g\left(y_0^2-y^2\right)}}dy\\ t=\sqrt{\frac{B}{g}}{\displaystyle \underset{-y_0}{\overset{y}{\int }}\sqrt{\frac{C+x}{(y_0-x)(y_0+x)}}}dx\end{array}}$

Donde C=A/B. Buscamos la solución a la integral

${\displaystyle \begin{array}{l}{\displaystyle \underset{b}{\overset{u}{\int }}\sqrt{\frac{x-c}{\left(a-x\right)(x-b)}}dx=2\sqrt{a-c}·E(\theta ,k)-2\sqrt{\frac{(a-u)(u-b)}{u-c}}}\\ \theta =\arcsin \sqrt{\frac{(a-c)(u-b)}{(a-b)(u-c)}},k=\sqrt{\frac{a-b}{a-c}}\end{array}}$

E(θ,k), se denomina integral elíptica incompleta de segunda especie. Identificamos: u=y, c=-C=-A/B, a=y₀, b=-y₀

${\displaystyle \begin{array}{l}t=2\sqrt{\frac{B}{g}}\left\{\sqrt{y_0+C}·E(\theta ,k)-\sqrt{\frac{(y_0-y)(y+y_0)}{y+C}}\right\}\\ \theta =\arcsin \sqrt{\frac{(y_0+C)(y+y_0)}{2y_0(y+C)}},k=\sqrt{\frac{2y_0}{y_0+C}}\end{array}}$

El periodo es el doble del tiempo que tarda el nivel del líquido en el recipiente de la derecha, en subir desde h-y₀ a h+y₀. Cuando el límite superior de la integral y=y₀

${\displaystyle \begin{array}{l}\theta =\arcsin (1)=\frac{\pi }{2},k=\sqrt{\frac{2y_0}{y_0+C}}\\ P=2\sqrt{\frac{B}{g}}{\displaystyle \underset{-y_0}{\overset{y_0}{\int }}\sqrt{\frac{C+x}{(y_0-x)(y_0+x)}}}dx=4\sqrt{\frac{B}{g}}\sqrt{y_0+C}·E(k)\end{array}}$

E(k), es una integral elíptica completa

Solución numérica

Consideremos el sistema formado por dos vasos comunicantes

• Radio del recipiente cilíndrico de la derecha r₂= 5 cm, se mantiene fijo
• Radio del recipiente cilíndrico de la izquierda r₁= 10 cm, mayor que r₂
• Radio del tubo horizontal, r_d=0.2 cm
• Longitud del tubo horizontal, d=10 cm

En el instante inicial t=0, los niveles del líquido en cada uno de los recipientes es

• Recipiente de la izquierda h₁= 10 cm, se mantiene fijo
• Recipiente de la derecha h₂= 20 cm, mayor que h₁

Calculamos la altura h de equilibrio

${\displaystyle h=\frac{r_1^2{h}_1+r_2^2{h}_2}{r_1^2+r_2^2}}$

Se deberá cumplir que 2h-h₂≥0. en caso contrario se modifica h₂

Calculamos el periodo P y resolvemos la ecuación diferencial por el procedimiento numérico ode45 de MATLAB. Las condiciones iniciales son: t=0, y₀=x₀₂=h₂-h, en reposo, dy/dt=0

El nivel del líquido en el recipiente de la derecha en el instante t es h₂=h+x₂=h+y

r2=5; % fijo
r1=10; %mayor que r2
h2=20; %mayor que h1
h1=10; %fijo
d=10; %tubo que comunica los recipientes
rd=0.2; 

%altura de equilibrio
h=(r1^2*h1+r2^2*h2)/(r1^2+r2^2);
if 2*h-h2<0
    disp('Diminuir la altura inicial')
    return;
end
A=h+r1^2*r2^2*d/(rd^2*(r1^2+r2^2));
B=1-r2^2/r1^2;
%periodo
if r1==r2
    P=2*pi*sqrt((h+r2^2*d/(2*rd^2))/9.8);
else
    k2=2*(h2-h)/(h2-h+A/B);
    [K,E]=ellipke(k2);
   P=4*sqrt(B/9.8)*sqrt(h2-h+A/B)*E;
end

f=@(t,x) [x(2);(-9.8*x(1)-B*x(2)^2/2)/(A+B*x(1))]; 
[t,x]=ode45(f,[0,P],[h2-h,0]);
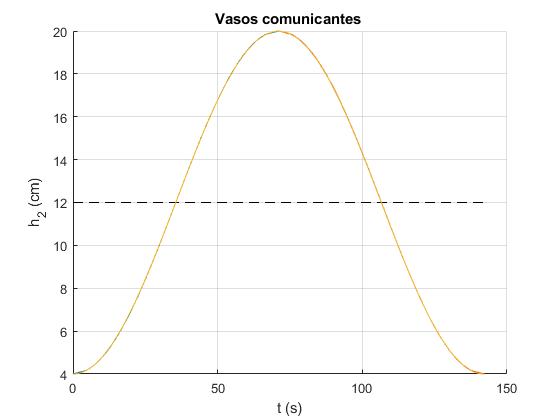
plot(t,x(:,1)+h)
line([0,P],[h,h],'lineStyle','--','color','k')
grid on
xlabel('t (s)')
ylabel('h_2 (cm)');
title('Vasos comunicantes ')

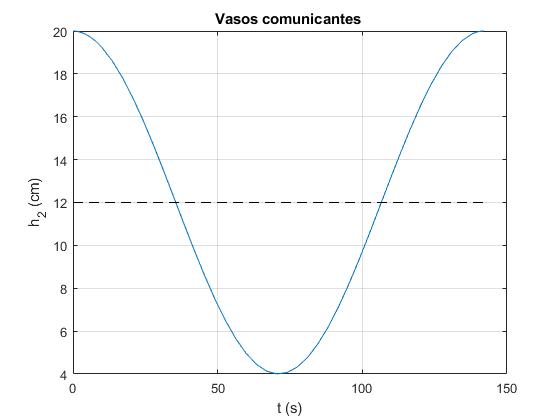
La línea a trazos señala la altura h de equilibrio. El periodo P en s, vale

P =  142.0929

Comprobamos que la energía se mantiene constante.

${\displaystyle \left(A+By\right){\left(\frac{dy}{dt}\right)}^2=g\left(y_0^2-y^2\right)}$

En el lado izquierdo, tenemos el cambio de energía cinética, en el derecho, el cambio de energía potencial, la suma debe anularse, ΔE_k+ΔE_p=0

>> (A+B*x(:,1)).*x(:,2).^2-9.8*((h2-h)^2-x(:,1).^2)
ans =
         0
    0.0000
   -0.0000
   ...
   -0.1115
   -0.1116

Solución analítica

La ecuación

${\displaystyle \begin{array}{l}t=2\sqrt{\frac{B}{g}}\left\{\sqrt{y_0+C}·E(\theta ,k)-\sqrt{\frac{(y_0-y)(y+y_0)}{y+C}}\right\}\\ \theta =\arcsin \sqrt{\frac{(y_0+C)(y+y_0)}{2y_0(y+C)}},k=\sqrt{\frac{2y_0}{y_0+C}}\end{array}}$

nos proporciona la ecuación implícita t=f(y). Damos valores a y en el intervalo -y₀≤y≤y₀, obteniendo el nivel de líquido en el recipiente derecho h+y en función del tiempo t durante medio periodo de la oscilación

Comprobamos que la solución analítica coincide con la solución utilizando procedimientos numéricos

r2=5; %cm fijo
r1=10; %mayor que r2
h2=20; %mayor que h1
h1=10; %fijo
d=10; %tubo que comunica los recipientes
rd=0.2; 

%altura de equilibrio
h=(r1^2*h1+r2^2*h2)/(r1^2+r2^2);
if 2*h-h2<0
    disp('Diminuir la altura inicial')
    return;
end
A=h+r1^2*r2^2*d/(rd^2*(r1^2+r2^2));
B=1-r2^2/r1^2;

%periodo
if r1==r2 %armónico
    P=2*pi*sqrt((h+r2^2*d/(2*rd^2))/9.8);
else
    k2=h2/(h2+A/B);
    [K,E]=ellipke(k2);
    P=4*sqrt(B/9.8)*sqrt(h2+A/B)*E;
end

%solución analítica
if r1==r2 %armónico
    w0=sqrt(9.8/(h+r2^2*d/(2*rd^2)));
    t=linspace(0,pi/w0,100);
    y=-(h2-h)*cos(w0*t);
else
    y=linspace(-(h2-h),(h2-h),100);
    k2=2*(h2-h)/(h2-h+A/B);
    th=asin(sqrt((h2-h+A/B)*(y+h2-h)./(2*(h2-h)*(y+A/B))));
    E=ellipticE(th,k2);
    t=2*sqrt(B/9.8)*(sqrt((h2-h)+A/B)*E-sqrt((h2-h-y).*(y+h2-h)./(y+A/B)));
end

hold on
plot(t,y+h)
plot(t+P/2,-y+h)
line([0,P],[h,h],'lineStyle','--','color','k')

%solución numérica
f=@(t,x) [x(2);(-9.8*x(1)-B*x(2)^2/2)/(A+B*x(1))]; 
[t,x]=ode45(f,[0,P],[-h2+h,0]);
plot(t,x(:,1)+h)

hold off
grid on
xlabel('t (s)')
ylabel('h_2 (cm)');
title('Vasos comunicantes ')

Actividades

Se introduce

• Radio del recipiente cilíndrico de la derecha r₂= 5 cm, se mantiene fijo
• Radio del recipiente cilíndrico de la izquierda r₁, mayor que r₂, en el control titulado Radio izquierda
• Radio del tubo horizontal, r_d=0.2 cm
• Longitud del tubo horizontal, d=10 cm

En el instante inicial t=0, los niveles del líquido en cada uno de los recipientes son

• Recipiente de la izquierda h₁= 10 cm, se mantiene fijo
• Recipiente de la derecha h₂, mayor que h₁ en el contro titulado Altura derecha

Calculamos la altura h de equilibrio. Si 2h-h₂<0, un mensaje nos invita a modificar la altura h₂ o el radio r₁

Ecuación de Bernoulli no estacionaria

El flujo Q no es constante, por lo que aplicamos aplicamos la ecuación de Bernoulli en el estado no estacionario a los puntos 1 y 2 (en color rojo) situados en la superficie libre del fluido a uno y otro lado del tubo en U

${\displaystyle \begin{array}{l}\left(p_1+\rho g{y}_1+\frac{1}{2}\rho v_1^2\right)-\left(p_2+\rho g{y}_2+\frac{1}{2}\rho v_2^2\right)=\frac{dQ}{dt}{\displaystyle \underset{1}{\overset{2}{\int }}\frac{ds}{A(s)}}\\ Q=\frac{dm}{dt}=\rho Av\end{array}}$

En este caso

${\displaystyle \left(p_0-\rho g{x}_1+\frac{1}{2}\rho v_1^2\right)-\left(p_0+\rho g{x}_2+\frac{1}{2}\rho v_2^2\right)=\rho \frac{d\left(v_2{S}_2\right)}{dt}{\left(\frac{h-x_1}{S_1}+\frac{d}{S}+\frac{h+x_2}{S_2}\right)}_{}}$

En un instante dado t, el nivel del líquido por debajo de la altura de equilibrio en el primer vaso es x₁ y en el segundo, el nivel está por encima x₂. Como el volumen de líquido no ha cambiado

S₁x₁=S₂x₂

Si v₁ es la velocidad del fluido en el primer recipiente y v₂ en el segundo Se cumplirá por la ecuación de continuidad que

S₁v₁=S₂v₂

${\displaystyle -g\frac{S_2}{S_1}{x}_2+\frac{1}{2}\frac{S_2^2}{S_1^2}{v}_2^2-g{x}_2-\frac{1}{2}{v}_2^2=S_2\frac{d{v}_2}{dt}{\left(\frac{h-x_1}{S_1}+\frac{d}{S}+\frac{h+x_2}{S_2}\right)}_{}}$

Denominamos y=x₂, dy/dt=v₂. Obtenemos la ecuación diferencial

${\displaystyle \begin{array}{l}\left\{\left(1+\frac{S_2}{S_1}\right)h+\frac{S_2}{S}d+\left(1-\frac{S_2^2}{S_1^2}\right)y\right\}\frac{d^{2}y}{d{t}^2}+\frac{1}{2}\left(1-\frac{S_2^2}{S_1^2}\right){\left(\frac{dy}{dt}\right)}^2+\left(1+\frac{S_2}{S_1}\right)g=0\\ \left\{h+\frac{S_2{S}_1}{\left(S_2+S_1\right)S}d+\left(1-\frac{S_2}{S_1}\right)y\right\}\frac{d^{2}y}{d{t}^2}+\frac{1}{2}\left(1-\frac{S_2}{S_1}\right){\left(\frac{dy}{dt}\right)}^2+g=0\end{array}}$

La misma que mediante la ecuación de Lagrange

Referencias

I.S. Gradshteyn, I.M. Ryzhik. Table of Integrals, Series, and Products. Seventh Edition. Elsevier (2007). 3.141, n° 16, pág. 267,

A.R. Kazachkov, V.A. Lykah, K.A. Minakova, E.S. Syrkin, O.Y. Tkachenko. Liquid nonlinear oscillatios in the U-tube system. Proceedings of the 5^th International Conference on Nonlinear Dynamics, ND-KhPI2016. September 27-30, 2016, Kharkov, Ukraine