Las ecuaciones de Navier-Stokes son

${\displaystyle \{\begin{array}{l}\rho \left(\frac{\partial u_x}{\partial t}+u_x\frac{\partial u_x}{\partial x}+u_y\frac{\partial u_x}{\partial y}+u_z\frac{\partial u_x}{\partial z}\right)=-\frac{\partial p}{\partial x}+\eta \left(\frac{{\partial }^2{u}_x}{\partial x^2}+\frac{{\partial }^2{u}_x}{\partial y^2}+\frac{{\partial }^2{u}_x}{\partial z^2}\right)\\ \rho \left(\frac{\partial u_y}{\partial t}+u_x\frac{\partial u_y}{\partial x}+u_y\frac{\partial u_y}{\partial y}+u_z\frac{\partial u_y}{\partial z}\right)=-\frac{\partial p}{\partial y}+\eta \left(\frac{{\partial }^2{u}_y}{\partial x^2}+\frac{{\partial }^2{u}_y}{\partial y^2}+\frac{{\partial }^2{u}_y}{\partial z^2}\right)\\ \rho \left(\frac{\partial u_z}{\partial t}+u_x\frac{\partial u_z}{\partial x}+u_y\frac{\partial u_z}{\partial y}+u_z\frac{\partial u_z}{\partial z}\right)=-\frac{\partial p}{\partial z}+\rho g+\eta \left(\frac{{\partial }^2{u}_z}{\partial x^2}+\frac{{\partial }^2{u}_z}{\partial y^2}+\frac{{\partial }^2{u}_z}{\partial z^2}\right)\end{array}}$

Donde ρ es la densidad y η la viscosidad. El eje Z es vertical y g es la aceleración de la gravedad

En el estado estacionario, independiente del tiempo t y para un fluido cuya viscosidad η=0

${\displaystyle \{\begin{array}{l}{u}_x\frac{\partial u_x}{\partial x}+u_y\frac{\partial u_x}{\partial y}+u_z\frac{\partial u_x}{\partial z}=-\frac{1}{\rho }\frac{\partial p}{\partial x}\\ u_x\frac{\partial u_y}{\partial x}+u_y\frac{\partial u_y}{\partial y}+u_z\frac{\partial u_y}{\partial z}=-\frac{1}{\rho }\frac{\partial p}{\partial y}\\ u_x\frac{\partial u_z}{\partial x}+u_y\frac{\partial u_z}{\partial y}+u_z\frac{\partial u_z}{\partial z}=-\frac{1}{\rho }\frac{\partial p}{\partial z}+g\end{array}}$

Líneas de corriente

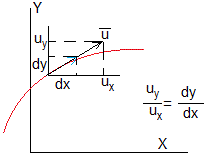
Una línea de corriente es aquella que es paralela al vector velocidad en cada punto

${\displaystyle \overrightarrow{u}(x,y,z,t)=u_x\widehat{i}+u_y\widehat{j}+u_z\widehat{k}}$

Definimos el vector desplazamiento a lo largo de la línea de corriente

${\displaystyle \overrightarrow{ds}=dx\widehat{i}+dy\widehat{j}+dz\widehat{k}}$

Como los dos vectores son paralelos

${\displaystyle \begin{array}{l}\overrightarrow{ds}\times \overrightarrow{u}=0\\ \left|\begin{array}{ccc}\widehat{i}& \widehat{j}& \widehat{k}\\ dx& dy& dz\\ u_x& u_y& u_z\end{array}\right|=0\\ \left(u_{z}dy-u_{y}dz\right)\widehat{i}-\left(u_{z}dx-u_{x}dz\right)\widehat{j}+\left(u_{y}dx-u_{x}dy\right)\widehat{k}=0\end{array}}$

La ecuación de las líneas de corriente

${\displaystyle \{\begin{array}{l}{u}_{z}dy=u_{y}dz\\ u_{z}dx=u_{x}dz\\ u_{y}dx=u_{x}dy\end{array}}$

La ecuación de Bernoulli

Multiplicamos la primera ecuación por dx, la segunda por dy y la tercera por dz

${\displaystyle \{\begin{array}{l}{u}_x\frac{\partial u_x}{\partial x}dx+u_y\frac{\partial u_x}{\partial y}dx+u_z\frac{\partial u_x}{\partial z}dx=-\frac{1}{\rho }\frac{\partial p}{\partial x}dx\\ u_x\frac{\partial u_y}{\partial x}dy+u_y\frac{\partial u_y}{\partial y}dy+u_z\frac{\partial u_y}{\partial z}dy=-\frac{1}{\rho }\frac{\partial p}{\partial y}dy\\ u_x\frac{\partial u_z}{\partial x}dz+u_y\frac{\partial u_z}{\partial y}dz+u_z\frac{\partial u_z}{\partial z}dz=-\frac{1}{\rho }\frac{\partial p}{\partial z}dz+gdz\end{array}}$

Para una línea de corriente

${\displaystyle \begin{array}{l}\{\begin{array}{l}{u}_x\frac{\partial u_x}{\partial x}dx+u_x\frac{\partial u_x}{\partial y}dy+u_x\frac{\partial u_x}{\partial z}dz=-\frac{1}{\rho }\frac{\partial p}{\partial x}dx\\ u_y\frac{\partial u_y}{\partial x}dx+u_y\frac{\partial u_y}{\partial y}dy+u_y\frac{\partial u_y}{\partial z}dz=-\frac{1}{\rho }\frac{\partial p}{\partial y}dy\\ u_z\frac{\partial u_z}{\partial x}dx+u_z\frac{\partial u_z}{\partial y}dy+u_z\frac{\partial u_z}{\partial z}dz=-\frac{1}{\rho }\frac{\partial p}{\partial z}dz+gdz\end{array}\\ \{\begin{array}{l}{u}_{x}d{u}_x=-\frac{1}{\rho }\frac{\partial p}{\partial x}dx\\ u_{y}d{u}_y=-\frac{1}{\rho }\frac{\partial p}{\partial y}dy\\ u_{z}d{u}_z=-\frac{1}{\rho }\frac{\partial p}{\partial z}dz+gdz\end{array}\\ u_{x}d{u}_x+u_{y}d{u}_y+u_{z}d{u}_z=-\frac{1}{\rho }\left(\frac{\partial p}{\partial x}dx+\frac{\partial p}{\partial y}dy+\frac{\partial p}{\partial z}dz\right)+gdz\\ \frac{1}{2}d{u}^2+\frac{1}{\rho }dp+gdz=0\end{array}}$

Esta es la ecuación de Bernoulli en forma diferencial

Proceso isotermo

La ecuación de un gas ideal es

${\displaystyle \begin{array}{l}pV=\frac{m}{M}RT\\ p=\frac{\rho }{M}RT\end{array}}$

R=8.3143 J/(K·mol) es la constante de los gases, p es la presión en Pa, ρ es la densidad en kg/m³. M es la masa molar en kg/mol, T es la temperatura en K

Integramos

${\displaystyle \begin{array}{l}\frac{1}{2}{u}^2+\frac{RT}{M}{\displaystyle \int \frac{dp}{p}}=\text{cte}\\ \frac{1}{2}{u}^2+\frac{RT}{M}\ln p=\text{cte}\\ \frac{1}{2}{u}_1^2+\frac{RT}{M}\ln p_1=\frac{1}{2}{u}_2^2+\frac{RT}{M}\ln p_2\end{array}}$

1 y 2 son dos puntos de la misma línea de corriente

Proceso adiabático

La ecuación de un proceso adiabático es

${\displaystyle \begin{array}{l}p{V}^{\gamma }=\text{cte}\\ \frac{p}{{\rho }^{\gamma }}=k\end{array}}$

γ es el índice adiabático, 7/5=1.4 para el aire (gas diatómico)

Integramos

${\displaystyle \begin{array}{l}\frac{1}{2}{u}^2+{\displaystyle \int \frac{dp}{{\left(\frac{p}{k}\right)}^{\frac{1}{\gamma }}}}=\text{cte}\\ \frac{1}{2}{u}^2+k^{\frac{1}{\gamma }}\frac{p^{-\frac{1}{\gamma }+1}}{-\frac{1}{\gamma }+1}=\text{cte}\\ \frac{1}{2}{u}^2+\frac{p}{\rho }\frac{\gamma }{\gamma -1}=\text{cte}\\ \frac{1}{2}{u}_1^2+\frac{p_1}{{\rho }_1}\frac{\gamma }{\gamma -1}=\frac{1}{2}{u}_2^2+\frac{p_2}{{\rho }_2}\frac{\gamma }{\gamma -1}\end{array}}$

Sea un gas que fluye por un tubo horizontal de sección variable

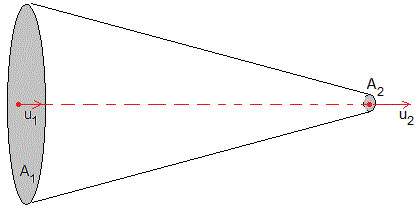
Definimos las variables adimensionales

${\displaystyle \alpha =\frac{A_1}{A_2},x=\frac{u_2}{u_1}}$

Donde A₁ y A₂ son las secciones del tubo y u₁ y u₂ las velocidades del gas

La ecuación de Bernoulli se escribe

${\displaystyle 1+\frac{c_1^2}{u_1^2}\frac{2}{\gamma -1}=x^2+\frac{p_2}{{\rho }_2}\frac{2\gamma }{\gamma -1}\frac{1}{u_1^2}}$

Donde c₁ es la velocidad del sonido

${\displaystyle c_1=\sqrt{\frac{\gamma p_1}{{\rho }_1}}}$

Por la ecuación de continuidad

${\displaystyle \begin{array}{l}{\rho }_1{A}_1{u}_1={\rho }_2{A}_2{u}_2\\ {\rho }_1\frac{\alpha }{x}={\rho }_2\end{array}}$

Teniendo en cuenta la ecuación del proceso adiabático

${\displaystyle \frac{p_1}{{\rho }_1^{\gamma }}=\frac{p_2}{{\rho }_2^{\gamma }}}$

Obtenemos

${\displaystyle \begin{array}{l}1+\frac{c_1^2}{u_1^2}\frac{2}{\gamma -1}=x^2+\frac{\frac{p_1{\rho }_2^{\gamma }}{{\rho }_1^{\gamma }}}{{\rho }_2}\frac{2\gamma }{\gamma -1}\frac{1}{u_1^2}\\ 1+\frac{c_1^2}{u_1^2}\frac{2}{\gamma -1}=x^2+\frac{p_1{\rho }_2^{\gamma -1}}{{\rho }_1^{\gamma }}\frac{2\gamma }{\gamma -1}\frac{1}{u_1^2}\\ 1+\frac{c_1^2}{u_1^2}\frac{2}{\gamma -1}=x^2+\frac{p_1{\left({\rho }_1\frac{\alpha }{x}\right)}^{\gamma -1}}{{\rho }_1^{\gamma }}\frac{2\gamma }{\gamma -1}\frac{1}{u_1^2}\\ 1+\frac{c_1^2}{u_1^2}\frac{2}{\gamma -1}=x^2+\frac{p_1}{{\rho }_1}{\left(\frac{\alpha }{x}\right)}^{\gamma -1}\frac{2\gamma }{\gamma -1}\frac{1}{u_1^2}\\ 1+\frac{c_1^2}{u_1^2}\frac{2}{\gamma -1}=x^2+\frac{c_1^2}{u_1^2}{\left(\frac{\alpha }{x}\right)}^{\gamma -1}\frac{2}{\gamma -1}\\ 1-x^2=\frac{c_1^2}{u_1^2}\frac{2}{\gamma -1}\left({\left(\frac{\alpha }{x}\right)}^{\gamma -1}-1\right)\\ {\left(\frac{\alpha }{x}\right)}^{\gamma -1}=1+\frac{u_1^2}{c_1^2}\frac{\gamma -1}{2}\left(1-x^2\right)\end{array}}$

El resultado final, es la ecuación implícita

${\displaystyle \alpha =x{\left(1+\frac{u_1^2}{c_1^2}\frac{\gamma -1}{2}\left(1-x^2\right)\right)}^{\frac{1}{\gamma -1}}}$

Representamos el cociente x=u₂/u₁ en función de α=A₁/A₂ para tres valores de u₁=3.4, 13.6, 20.4 m/s. La velocidad del sonido c₁=340.3 m/s

c1=340.3; %velocidad del sonido 
g=7/5; %índice adibático
hold on
for u1=[3.4, 13.6,20.4]
    f=@(x) x.*(1+u1^2*(g-1)*(1-x.^2)/(2*c1^2)).^(1/(g-1));
    fplot(f,[0,10],'displayName',num2str(u1))
end
hold off
grid on
xlabel('u_2/u_1')
ylabel('A_1/A_2')
legend('-DynamicLegend','location','best')
title('Velocidad, sección')
view(90,-90)

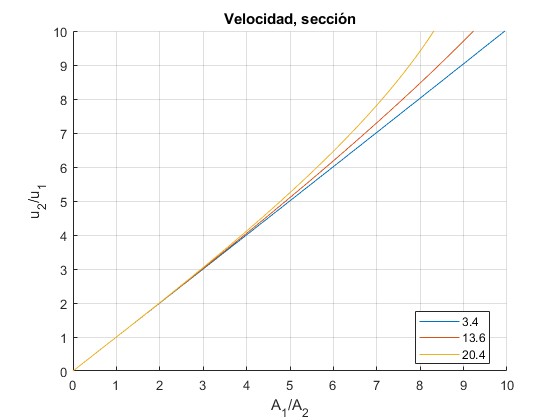
Para bajas velocidades u₁, la función x(α) se aproxima a una línea recta (color azul)

Vaciado de un recipiente que contiene gas a presión

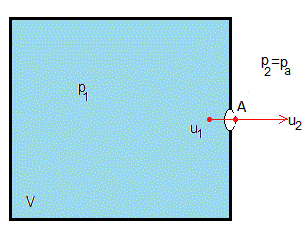
Supondremos un recipiente de volumen V que tiene un pequeño agujero de sección A. Su presión inicial es p₀. Al cabo de un cierto tiempo t_f la presión del recipiente se iguala a la presión atmosférica p_a

Un problema similar se trata en la página titulada Efusión de un gas

La ecuación de continuidad nos dice que

${\displaystyle {\rho }_1{A}_1{u}_1={\rho }_2{A}_2{u}_2}$

Si la sección del recipiente A₁>>A₂=A entonces u₁≈0

Proceso isotérmico

Aproximando u₁≈0, despejamos la velocidad de salida del gas u₂

${\displaystyle \begin{array}{l}\frac{RT}{M}\ln p_1=\frac{1}{2}{u}_2^2+\frac{RT}{M}\ln p_2\\ u_2=\sqrt{\frac{2RT}{M}\ln \frac{p_1}{p_a}}\end{array}}$

Con p₂=p_a. La masa de gas que pierde el recipiente en la unidad de tiempo es

${\displaystyle \frac{dm}{dt}=-{\rho }_1{u}_{2}A=-{\rho }_{1}A\sqrt{\frac{2RT}{M}\ln \frac{p_1}{p_a}}=-p_{1}A\sqrt{\frac{2M}{RT}\ln \frac{p_1}{p_a}}}$

La presión en el recipiente disminuye con el tiempo

${\displaystyle \begin{array}{l}V·d{p}_1=\frac{dm}{M}RT\\ d{p}_1=-p_1\frac{A}{V}\sqrt{\frac{2RT}{M}\ln \frac{p_1}{p_a}}dt=-p_1\sqrt{\ln \frac{p_1}{p_a}}\frac{dt}{\tau },\tau =\frac{V}{A}\sqrt{\frac{M}{2RT}}\end{array}}$

Integramos

${\displaystyle {\displaystyle \underset{p_0}{\overset{p}{\int }}\frac{d{p}_1}{p_1\sqrt{\ln \frac{p_1}{p_a}}}}=-\frac{1}{\tau }{\displaystyle \underset{0}{\overset{t}{\int }}dt}}$

Hacemos el cambio de variable

${\displaystyle \begin{array}{l}u=\ln \frac{p_1}{p_a}=\ln p_1-\ln p_a,du=\frac{dp}{p_1}\\ {\displaystyle \int \frac{du}{\sqrt{u}}}=2\sqrt{u}=2\sqrt{\ln \frac{p_1}{p_a}}\end{array}}$

El resultado de la integral es

${\displaystyle \begin{array}{l}2\left(\sqrt{\ln \frac{p}{p_a}}-\sqrt{\ln \frac{p_0}{p_a}}\right)=-\frac{t}{\tau }\\ \sqrt{\ln \frac{p}{p_a}}=-\frac{t}{2\tau }+\sqrt{\ln \frac{p_0}{p_a}}\\ \ln \frac{p}{p_a}={\left(-\frac{t}{2\tau }+\sqrt{\ln \frac{p_0}{p_a}}\right)}^2\\ p=p_a\exp {\left(-\frac{t}{2\tau }+\sqrt{\ln \frac{p_0}{p_a}}\right)}^2\end{array}}$

La presión p del recipiente se iguala a la presión atmosférica en el instante

${\displaystyle \begin{array}{l}\frac{t_f}{2\tau }=\sqrt{\ln \frac{p_0}{p_a}}\\ t_f=2\tau \sqrt{\ln \frac{p_0}{p_a}}\end{array}}$

Representamos la presión p en kPa en el recipiente en función del tiempo t en s. Datos

• Presión atmosférica, p_a=1.013·10⁵ Pa
• p₀=3·p_a es la presión inicial del recipiente
• Volumen del recipiente V=2 litros
• El agujero es de 0.5 mm de diámetro
• R=8.3143 J/(K·mol) es la constante de los gases
• M=28.97 g/mol es la masa molar promedio del aire seco,
• T=293 K es la temperatura

pa=1.013e5; %presión atmosférica en Pa
M=28.97/1000; %masa molar promedio del aire seco
A=pi*(0.0005/2)^2; %sección 0.5 mm de diámetro
p0=3*pa; %presión inicial del recipiente
V=2/1000; %volumen del recipiente 2 litros
R=8.3143; %constante de los gases
T=293; %temperatura K
tau=V*sqrt(M/(2*R*T))/A;
tf=2*tau*sqrt(log(p0/pa));
p=@(t) pa*exp((-t/(2*tau)+sqrt(log(p0/pa))).^2)/1000;% en kPa
hold on
fplot(p,[0,tf])
plot(tf,pa/1000,'ro','markersize',3,'markerfacecolor','r')

line([0,tf],[pa/1000,pa/1000],'lineStyle','--')
line([tf,tf],[0,pa/1000],'lineStyle','--')
hold off
grid on
xlabel('t (s)')
ylabel('p (kPa)')
title('Presión. Isoterma')

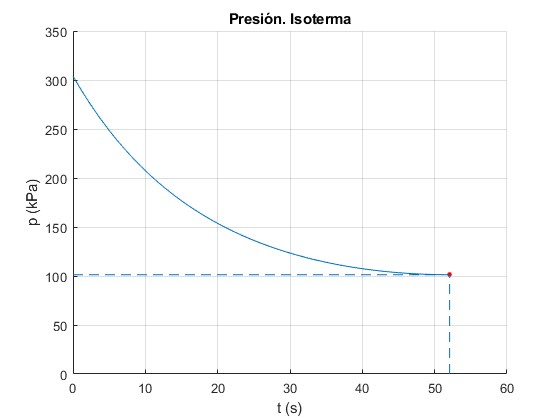
La presión p del recipiente se iguala a la presión atmosférica en el instante

>> tf
tf =   52.0673

Proceso adiabático

Aproximando u₁≈0, despejamos la velocidad de salida del gas u₂

${\displaystyle \begin{array}{l}\frac{p_1}{{\rho }_1}\frac{\gamma }{\gamma -1}=\frac{1}{2}{u}_2^2+\frac{p_2}{{\rho }_2}\frac{\gamma }{\gamma -1}\\ u_2^2=\frac{2\gamma }{\gamma -1}\left(\frac{p_1}{{\rho }_1}-\frac{p_2}{{\rho }_2}\right)=\frac{2\gamma }{\gamma -1}\left(\frac{p_1}{{\rho }_1}-\frac{p_2}{\frac{{\rho }_1{p}_2^{1/\gamma }}{p_1^{1/\gamma }}}\right)=\frac{2\gamma }{\gamma -1}\frac{p_1}{{\rho }_1}\left(1-{\left(\frac{p_2}{p_1}\right)}^{1-1/\gamma }\right)\end{array}}$

La masa de gas que pierde el recipiente en la unidad de tiempo es

${\displaystyle \begin{array}{l}\frac{dm}{dt}=-{\rho }_1{u}_{2}A=-A\sqrt{\frac{2\gamma }{\gamma -1}{\rho }_1{p}_1\left(1-{\left(\frac{p_2}{p_1}\right)}^{1-1/\gamma }\right)}=-A\sqrt{\frac{2\gamma }{1-\gamma }}\sqrt{{\rho }_2{p}_1{\left(\frac{p_1}{p_2}\right)}^{1/\gamma }\left(1-{\left(\frac{p_2}{p_1}\right)}^{1-1/\gamma }\right)}\\ -A\sqrt{\frac{2\gamma }{\gamma -1}}{\rho }_2\sqrt{\frac{p_1}{{\rho }_2}{\left(\frac{p_1}{p_2}\right)}^{1/\gamma }\frac{p_2}{p_2}\left(1-{\left(\frac{p_2}{p_1}\right)}^{1-1/\gamma }\right)}=-A{\rho }_2{c}_2\sqrt{\frac{2}{\gamma -1}}\sqrt{{\left(\frac{p_1}{p_2}\right)}^{1/\gamma +1}\left(1-{\left(\frac{p_2}{p_1}\right)}^{1-1/\gamma }\right)}\\ =-A{\rho }_2{c}_2\sqrt{\frac{2}{\gamma -1}}\sqrt{{\left(\frac{p_1}{p_2}\right)}^{(\gamma +1)/\gamma }-{\left(\frac{p_1}{p_2}\right)}^{2/\gamma }}\end{array}}$

Donde $c_2=\sqrt{\frac{\gamma p_2}{{\rho }_2}}$, es la velocidad del sonido

La presión en el recipiente disminuye con el tiempo

${\displaystyle \begin{array}{l}V·d{p}_1=\frac{dm}{M}RT\\ \frac{d{p}_1}{dt}=-\frac{RT}{M}\frac{A}{V}{\rho }_2{c}_2\sqrt{\frac{2}{\gamma -1}}\sqrt{{\left(\frac{p_1}{p_2}\right)}^{(\gamma +1)/\gamma }-{\left(\frac{p_1}{p_2}\right)}^{2/\gamma }}\\ {\displaystyle \underset{p_0}{\overset{p}{\int }}\frac{d{p}_1}{\sqrt{{\left(\frac{p_1}{p_2}\right)}^{(\gamma +1)/\gamma }-{\left(\frac{p_1}{p_2}\right)}^{2/\gamma }}}}=-\frac{RT}{M}\frac{A}{V}{\rho }_2{c}_2\sqrt{\frac{2}{\gamma -1}}{\displaystyle \underset{0}{\overset{t}{\int }}dt}\end{array}}$

Tomando la presión p₂=p_a y la densidad ρ₂=ρ_a. c₂=c_a es la velocidad de propagación del sonido en el aire a la presión atmosférica y a la temperatura ambiente T=293 K

${\displaystyle t=-\frac{M}{RT}\frac{V}{A}\frac{1}{{\rho }_a{c}_a}\sqrt{\frac{\gamma -1}{2}}{\displaystyle \underset{p_0}{\overset{p}{\int }}\frac{d{p}_1}{\sqrt{{\left(\frac{p_1}{p_a}\right)}^{(\gamma +1)/\gamma }-{\left(\frac{p_1}{p_a}\right)}^{2/\gamma }}}}}$

Obtenemos una ecuación implícita de la presión p del recipiente en función del tiempo t. Por otra parte, la integral se ha de resolver de forma numérica mediante el procedimiento integral de MATLAB

Representamos la presión p del recipiente en función del tiempo t, hasta que se iguala a la presión atmosférica. Los datos adicionales que precisamos son

• Índice adiabático de aire γ=7/5=1.4 (gas diatómico)
• Densidad del aire, ρ_a=1.2 kg/m³

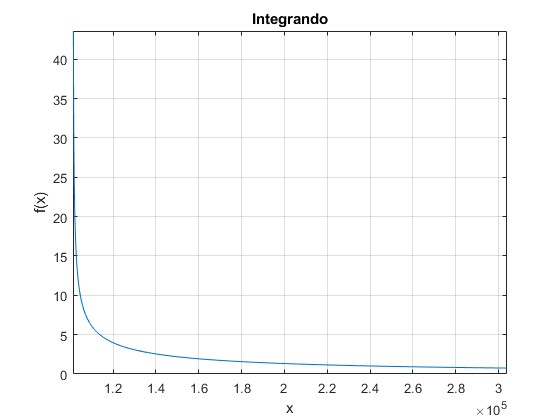
Tenemos que calcular el resultado de una integral impropia, ya que el integrando f(p₁) tiende a infinito cuando p₁→p_a

pa=1.013e5; %presión atmosférica en Pa
M=28.97/1000; %masa molar promedio del aire seco
A=pi*(0.0005/2)^2; %sección 0.5 mm de diámetro
p0=3*pa; %presión inicial del recipiente
V=2/1000; %volumen del recipiente 2 litros
R=8.3143; %constante de los gases
T=293; %temperatura K
g=7/5; %índice adibático
rho_a=1.2; %densidad del aire
ca=sqrt(g*pa/rho_a); %velocidad del sonido en el aire
k=M*V*sqrt((g-1)/2)/(R*T*A*rho_a*ca); %cte de proporcionalidad
f=@(x) 1./sqrt((x/pa).^((g+1)/g)-(x/pa).^(2/g));
fplot(f,[pa,p0])
grid on
xlabel('x')
ylabel('f(x)')
title('Integrando')

pa=1.013e5; %presión atmosférica en Pa
M=28.97/1000; %masa molar promedio del aire seco
A=pi*(0.0005/2)^2; %sección 0.5 mm de diámetro
p0=3*pa; %presión inicial del recipiente
V=2/1000; %volumen del recipiente 2 litros
R=8.3143; %constante de los gases
T=293; %temperatura K
g=7/5; %índice adibático
rho_a=1.2; %densidad del aire
ca=sqrt(g*pa/rho_a); %velocidad del sonido en el aire
k=M*V*sqrt((g-1)/2)/(R*T*A*rho_a*ca); %cte de proporcionalidad
f=@(x) 1./sqrt((x/pa).^((g+1)/g)-(x/pa).^(2/g));
pp=linspace(pa,p0, 100);
t=zeros(1, length(pp));
j=1;
for p=pp
    t(j)=-k*integral(f,p0,p);
    j=j+1;
end
plot(t,pp/1000)

grid on
xlabel('t (s)')
ylabel('p (kPa)')
title('Presión. Adibática')

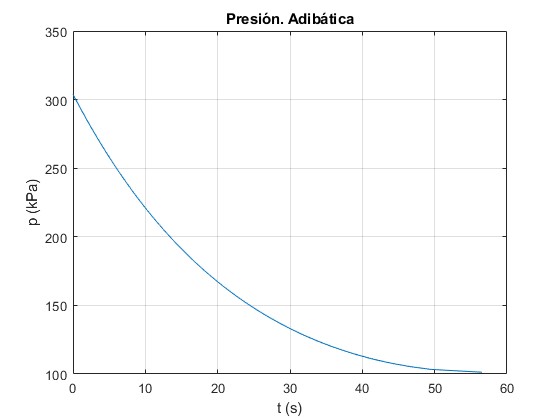
La presión p del recipiente se iguala a la presión atmosférica en el instante

>> t(1)
ans =   56.5428

Referencias

R DeLuca, P Desideri. Wind energy: an application of Bernoulli’s theorem generalized to isentropic flow of ideal gases. Eur. J. Phys. 34 (2013) pp. 189–197

Keith Atkin. The spacecraft decompression problem. Phys. Educ. 59 (2024) 015035

Carl E Mungan. Comment on ‘The spacecraft decompression problem’. Phys. Educ. 59 (2024) 038003