Analizamos en esta página, un tubo en forma de U que gira alrededor de un eje que pasa por el brazo vertical izquierdo. Cuando está en reposo, la altura de líquido, de densidad ρ, en ambos brazos verticales es h y la distancia entre los mismos es d. Supondremos que la sección S del tubo es muy pequeña.

Situación de equilibrio

Nos situamos en el Sistema de Referencia no Inercial vinculado al tubo que gira.

Brazo horizontal

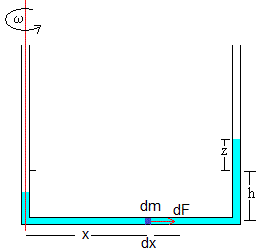
Al girar el tubo, la fuerza centrífuga actúa en los elementos del líquido situados en el brazo horizontal. La fuerza centrífuga que actúa sobre un elemento de masa dm situado a una distancia x del eje de rotación es

dF_c=ω²·x·dm=ρSω²x·dx

La fuerza centrífuga total sobre el líquido situado en el brazo horizontal es

${\displaystyle F_c={\displaystyle \underset{0}{\overset{d}{\int }}\rho S{\omega }^{2}x·dx}=\frac{1}{2}\rho S{\omega }^2{d}^2}$

Brazos verticales

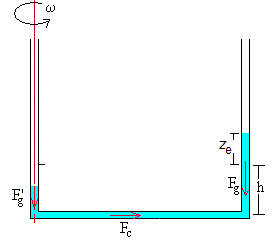
El peso del líquido contenido en el brazo vertical más alejado del eje de rotación es F_g=ρSg(h+z)  y actúa en su centro de masa a una altura (h+z)/2

El peso del líquido contenido en el brazo vertical más cercano del eje de rotación es F’_g=ρSg(h-z) y actúa en su centro de masa a una altura (h-z)/2

Equilibrio

En el equilibrio, la suma de fuerzas sobre el líquido contenido en el tubo debe ser cero

F_c+F'_g-F_g=0

${\displaystyle \begin{array}{l}\frac{1}{2}\rho S{\omega }^2{d}^2+\rho S(h-z)g-\rho S(h+z)g=0\\ {\omega }^2=\frac{4gz}{d^2}\end{array}}$

Cuando la velocidad angular es ω, el desplazamiento de equilibrio es z_e es

${\displaystyle z_e=\frac{d^2{\omega }^2}{4g}}$

A medida que incrementamos la velocidad angular de rotación ω, la altura z de líquido por encima de la de equilibrio h, en el brazo vertical más alejado del eje de rotación, va creciendo proporcionalmente ω² y decrece en el brazo más cercano al eje. Cuando z_e=h, desaparece el líquido en este brazo vertical. La velocidad angular ω vale

${\displaystyle \omega =2\frac{\sqrt{gh}}{d}}$

Energías

Calculamos las energías cinética y potencial del líquido contenido en un tubo en forma de U gira alrededor de un eje que pasa por el brazo vertical izquierdo

Energía potencial

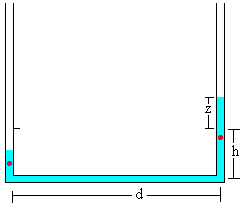
Comparamos la energía potencial en la situación de equilibrio en reposo (los dos brazos verticales tienen altura h) con la energía potencial cuando el desnivel del líquido en las dos brazos es 2z. Esta parte, ya se ha discutido en el primer apartado

El líquido contenido en el brazo horizontal no cambia su energía potencial. Los centros de masas de las columnas verticales de fluido se han marcado mediante un punto de color rojo, cuya altura es la mitad de la longitud de dicha columna.

• La energía potencial, referida al suelo, vale

ρSh·g·h/2+ρSh·g·h/2=ρS·g·h²

• En el instante t, el desnivel del líquido en las dos brazos es 2z, la energía potencial referida al suelo es.

ρS(h-x)g(h-x)/2+ρS(h+x)g(h+x)/2=ρS·g(h²+z²)

La variación de energía potencial es

E_p=ρS·g·z²

Energía cinética

Si el fluido se mueve en el tubo con velocidad dz/dt. Su energía cinética es

${\displaystyle E_t=\frac{1}{2}\rho S(d+2h){\left(\frac{dz}{dt}\right)}^2}$

Por otra parte, el tubo gira con velocidad angular ω=dθ/dt.

• El momento de inercia de la parte horizontal del tubo es (ρSd)d²/3, de una varilla que gira alrededor de un eje perpendicular que pasa por su extremo

• El momento de inercia del de la parte vertical izquierda del tubo es nulo

• El momento de inercia de la parte vertical derecha del tubo es ρS(h+z)d². Una masa que dista d del eje de rotación

La energía cinética de rotación es

${\displaystyle E_r=\frac{1}{2}\left\{\frac{1}{3}\left(\rho Sd\right)d^2+\left(\rho S(h+z)\right)d^2\right\}{\left(\frac{d\theta }{dt}\right)}^2=\frac{1}{2}\rho S{d}^2\left(\frac{d}{3}+h+z\right){\left(\frac{d\theta }{dt}\right)}^2}$

Ecuación del movimiento

La Lagrangiana L=E_t+E_r-E_p es

${\displaystyle L=\frac{1}{2}\rho S(d+2h){\left(\frac{dz}{dt}\right)}^2+\frac{1}{2}\rho S{d}^2\left(z+h+\frac{d}{3}\right){\left(\frac{d\theta }{dt}\right)}^2-\rho Sg{z}^2}$

La ecuación del movimiento del fluido en el tubo es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{z}}\right)-\frac{\partial L}{\partial z}=0\\ (d+2h)\frac{d^{2}z}{d{t}^2}+2gz-\frac{1}{2}{d}^2{\left(\frac{d\theta }{dt}\right)}^2=0\end{array}}$

Como la Lagrangiana no depende del ángulo θ, hay una cantidad que se conserva

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ \frac{\partial L}{\partial \dot{\theta }}=\text{cte}\\ \rho d^2\left(z+h+\frac{d}{3}\right)\left(\frac{d\theta }{dt}\right)=\text{cte}\\ \left(z+h+\frac{d}{3}\right)\left(\frac{d\theta }{dt}\right)=\left(z_0+h+\frac{d}{3}\right){\omega }_0\end{array}}$

z₀ es el desplazamiento del fluido en el tubo cuando la velocidad angular de rotación es ω₀

La ecuación diferencial que describe el movimiento del fluido en el tubo es

${\displaystyle (d+2h)\frac{d^{2}z}{d{t}^2}+2gz-\frac{1}{2}{d}^2\frac{{\left(z_0+h+\frac{d}{3}\right)}^2{\omega }_0^2}{{\left(z+h+\frac{d}{3}\right)}^2}=0}$

Resolvemos la ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales: en el instante t=0, z=z₀, dz/dt=0, dθ/dt=ω₀

La energía del tubo en U es la suma de las energías cinéticas y potencial gravitatoria, E=E_t+E_r+E_p

${\displaystyle E=\frac{1}{2}\rho S(d+2h){\left(\frac{dz}{dt}\right)}^2+\frac{1}{2}\rho S{d}^2\frac{{\left(z_0+h+\frac{d}{3}\right)}^2{\omega }_0^2}{\left(z+h+\frac{d}{3}\right)}+\rho Sg{z}^2}$

La energía se mantiene constante e igual a la inicial con dz/dt=0 y z=z₀

Resolvemos la ecuación diferencial en z con los datos:

• Distancia entre las dos brazos verticales, d=2 m
• Altura del líquido en los tubos verticales, en reposo, h=0.6 m
• Velocidad angular inicial de rotación, ω₀=1 rad/s.
• Para esta velocidad angular de rotación ω₀, el desplazamiento de equilibrio es z_e=0.102, comprobamos que z_e<h=0.6

Para que la columna de fluido oscile, el desplazamiento inicial z₀ tiene que ser diferente del de equilibrio z_e. Supongamos que z₀=0.

Representamos

• El desplazamiento z del fluido en el brazo vertical, respecto de la situación en reposo, en función del tiempo t
• La velocidad angular de rotación ω=dθ/dt, en función del tiempo t

Si observamos que z>h (desaparece el líquido del tubo vertical izquierdo) habrá que repetir el cálculo dismininuyendo la velocidad angular de rotación ω₀ o incrementando el nivel inicial h de líquido en el tubo vertical

d=2; %brazo horizontal
h=0.6; %altura inicial en el brazo vertical
w0=1; %velocidad angular inicial de rotación

z0=0; %desplazamiento inicial
f=@(t,x) [x(2);-2*9.8*x(1)/(d+2*h)+d^2*(z0+h+d/3)^2*w0^2/
(2*(d+2*h)*(x(1)+h+d/3)^2)]; 
[t,x]=ode45(f,[0,5],[z0,0]);
subplot(2,1,1)
plot(t,x(:,1))
grid on
xlabel('t')
ylabel('z');
title('Oscilador, z')
subplot(2,1,2)
w=(z0+h+d/3)*w0./(x(:,1)+h+d/3);
plot(t,w)
grid on
xlabel('t')
ylabel('\omega');
title('Velocidad angular de rotación')

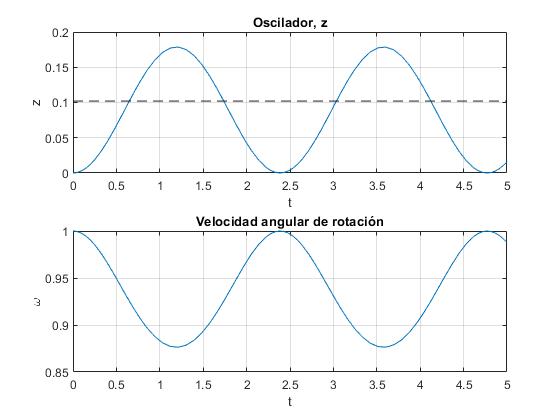
Con el cursor Data Tip medimos el periodo P≈2.4, de las oscilaciones en la ventana gráfica

Comprobamos que la energía E=E_t+E_r+E_p se conserva

>> E=(d+2*h)*x(:,2).^2/2+d^2*(z0+h+d/3)^2*w0^2./(2*(x(:,1)+h+d/3))+9.8*x(:,1).^2
E =
    2.5333
    2.5333
   ...

Como apreciamos, ω₀ es la velocidad angular máxima, a medida que se desplaza el fluido hacia el brazo derecho, el momento de inercia aumenta y disminuye la velocidad angular de rotación ω

Aproximación

Cuando los desplazamientos z respecto de la posición de equilibrio, z_e son pequeños, en la ecuación del movimiento sustituimos z, por z=z_e+ζ.

${\displaystyle \begin{array}{l}(d+2h)\frac{d^2(\zeta +z_e)}{d{t}^2}+2g(\zeta +z_e)=\frac{1}{2}{d}^2\frac{{\left(z_0+h+\frac{d}{3}\right)}^2{\omega }_0^2}{{\left(\zeta +z_e+h+\frac{d}{3}\right)}^2}\\ (d+2h)\frac{d^2\zeta }{d{t}^2}+2g(\zeta +z_e)=\frac{1}{2}{d}^2\frac{{\left(z_0+h+\frac{d}{3}\right)}^2{\omega }_0^2}{{\left(z_e+h+\frac{d}{3}\right)}^2{\left(1+\frac{\zeta }{z_e+h+\frac{d}{3}}\right)}^2}\end{array}}$

Hacemos la aproximación, 1/(1+x)²≈1-2x, cuando x<<1

>> syms x;
>> taylor(1/(1+x)^2,x)
ans =- 6*x^5 + 5*x^4 - 4*x^3 + 3*x^2 - 2*x + 1

${\displaystyle \begin{array}{l}(d+2h)\frac{d^2\zeta }{d{t}^2}+2g(\zeta +z_e)\approx \frac{1}{2}{d}^2\frac{{\left(z_0+h+\frac{d}{3}\right)}^2{\omega }_0^2}{{\left(z_e+h+\frac{d}{3}\right)}^2}\left(1-2\frac{\zeta }{z_e+h+\frac{d}{3}}\right)\\ \frac{d^2\zeta }{d{t}^2}+\frac{1}{d+2h}\left\{2g+d^2\frac{{\left(z_0+h+\frac{d}{3}\right)}^2{\omega }_0^2}{{\left(z_e+h+\frac{d}{3}\right)}^3}\right\}\zeta =\frac{1}{d+2h}\left\{\frac{1}{2}{d}^2\frac{{\left(z_0+h+\frac{d}{3}\right)}^2{\omega }_0^2}{{\left(z_e+h+\frac{d}{3}\right)}^2}-2g{z}_e\right\}\end{array}}$

Se trata de la ecuación de un MAS de frecuencia angular Ω o periodo 2π/Ω

${\displaystyle {\Omega }^2=\frac{1}{d+2h}\left\{2g+d^2\frac{{\left(z_0+h+\frac{d}{3}\right)}^2{\omega }_0^2}{{\left(z_e+h+\frac{d}{3}\right)}^3}\right\}}$

d=2; %brazo horizontal
h=0.6; %altura inicial en el brazo vertical
w0=1; %velocidad angular inicial de rotación

z0=0; %desplazamiento inicial
ze=d^2*w0^2/(4*9.8); %equilibrio
W=sqrt((2*9.8+d^2*(z0+h+d/3)^2*w0^2/(ze+h+d/3)^3)/(d+2*h));
P=2*pi/W; %periodo
disp(P)

  2.3907

En la ventana gráfica medimos un periodo similar, utilizando el cursor Data Tip

Actividades

Se introduce

• La velocidad angular inicial de rotación ω₀, en el control titulado Velocidad angular inicial
• La altura inicial h de líquido en los brazos verticales, cuando el tubo U está en reposo, en el control titulado Altura inicial
• La distancia entre los brazos verticales del tubo se ha fijado, d=2 m
• El desplazamiento inicial del fluido, cuando el tubo gira con velocidad angular ω₀, se ha fijado en z₀=0

Se pulsa el botón titulado Nuevo y a continuación, ►. El tubo empieza a girar con velocidad angular ω₀

Observamos el movimiento del fluido en el tubo en forma de U y del tubo girando alrededor del eje que pasa por el brazo izquierdo. Se proporcionan los datos

• Tiempo t, se puede medir el periodo de una oscilación
• Desplazamiento z del fluido, respecto d ela situación de equilibrio en reposo
• Velocidad angular de rotación ω.
• La energía del tubo en U que permenece constante e igual a la inicial

Si desaparece el líquido del tubo vertical izquierdo, z>h, un mensaje nos lo advierte y el programa interactivo se detiene. Se invita al lector a disminuir la velocidad angular inicial de rotación ω₀ o incrementar el nivel inicial h de líquido en el tubo vertical

Referencias

Lim Yung-kuo. Problems and Solutions on Mechanics. World Scientific (1994). Problem 2073, pp. 629-632