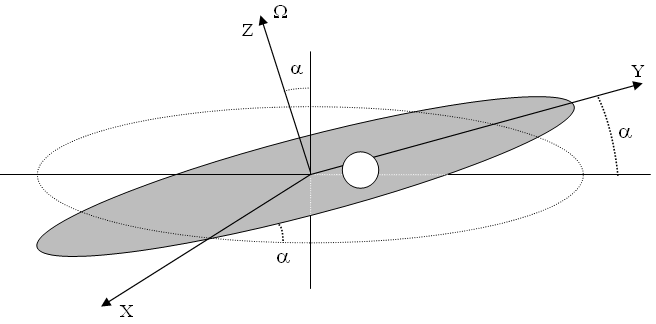
Cuando la plataforma es horizontal la esfera describe una órbita circular con una velocidad angular que es las dos séptimas partes de la velocidad angular de la plataforma. Cuando se inclina la plataforma, se superpone al movimiento circular un movimiento rectilíneo con velocidad constante hacia un lado (no a lo largo de la pendiente) denominada velocidad de deriva.

Ecuaciones del movimiento de la esfera

Para describir el movimiento de la esfera, situamos el Sistema de Referencia Inercial del siguiente modo: eje Y a lo largo de la plataforma inclinada un ángulo α, el eje X perpendicular al mismo y el eje Z perpendicular al plano de la plataforma, tal como se muestra en las figuras.

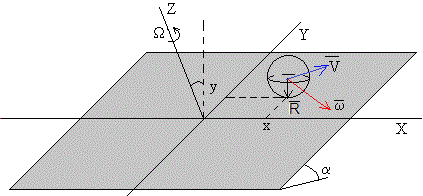
En un instante dato t, la esfera se encuentra en la posición (x, y) con velocidad, $\overrightarrow{V}$ , la velocidad angular de rotación es $\overrightarrow{\omega }$ rodando sin deslizar sobre la plataforma. La velocidad del punto P de contacto de la esfera con la plataforma es

${\displaystyle \begin{array}{l}{\overrightarrow{v}}_p=\overrightarrow{V}+\overrightarrow{\omega }\times \overrightarrow{R}\hfill \\ {\overrightarrow{v}}_p=\left(\begin{array}{c}{V}_x\\ V_y\\ 0\end{array}\right)\left(\begin{array}{ccc}\widehat{i}& \widehat{j}& \widehat{k}\\ {\omega }_x& {\omega }_y& {\omega }_z\\ 0& 0& -R\end{array}\right)=(V_x-R{\omega }_y)\widehat{i}+(V_y+R{\omega }_x)\widehat{j}\hfill \end{array}}$

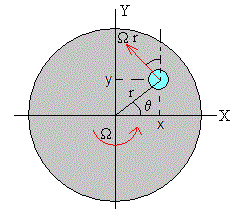
Si el punto de contacto P dista r del eje de rotación de la plataforma que gira con velocidad angular Ω. Las componentes de la velocidad del punto P

v_x=-Ω·r·sinθ=-Ω·y
v_y=Ω·r·cosθ=Ω·x

Para que la esfera ruede sin deslizar, el punto de contacto P debe de estar en reposo respecto de la plataforma. Se cumplirá por tanto,

-Ω·y=V_x-ω_y·R
Ω·x=V_y+ω_x·R

La condición de rodar sin deslizar V_c=ωR, se transforma en esta condición para una plataforma en rotación con velocidad angular constante Ω

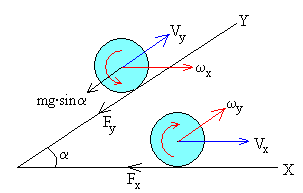
Las fuerzas sobre la esfera son:

• El peso mg
• La reacción del plano N
• La fuerza de rozamiento F en el punto de contacto P, cuyo valor y dirección en el plano son desconocidos

Sean F_x y F_y las componentes de la fuerza de rozamiento en el punto P de contacto de la esfera con el plano en rotación.

Ecuaciones del movimiento

• Ecuación del movimiento de traslación del centro de masas

${\displaystyle \begin{array}{l}m\frac{d{V}_x}{dt}=-F_x\\ m\frac{d{V}_y}{dt}=-F_y-mg\text{sin}\alpha \end{array}}$

• Ecuación del movimiento de rotación alrededor de un eje que pasa por el centro de masas

${\displaystyle \begin{array}{l}{I}_c\frac{d{\omega }_x}{dt}=-F_{y}R\\ I_c\frac{d{\omega }_y}{dt}=F_{x}R\end{array}}$

La componente ω_z de la velocidad angular permanece constante

Para una esfera la fórmula del momento de inercia es I_c=2mR²/5

Eliminamos las dos componentes desconocidas de la fuerza de rozamiento F_x, y F_y en las ecuaciones del movimiento.

${\displaystyle \begin{array}{l}\frac{d{V}_x}{dt}=-\frac{2}{5}R\frac{d{\omega }_y}{dt}\\ \frac{d{V}_y}{dt}=\frac{2}{5}R\frac{d{\omega }_x}{dt}-g·\text{sin}\alpha \end{array}}$

Derivamos respecto del tiempo las ecuaciones (1)

${\displaystyle \begin{array}{l}-\Omega V_y=\frac{d{V}_x}{dt}-R\frac{d{\omega }_y}{dt}\\ \Omega V_x=\frac{d{V}_y}{dt}+R\frac{d{\omega }_x}{dt}\end{array}}$

Eliminamos las derivadas de las componentes de la velocidad angular dω_x/dt, y dω_y/dt, y obtenemos las ecuaciones diferenciales del movimiento del c.m. de la esfera.

${\displaystyle \begin{array}{l}\frac{7}{2}\frac{d{V}_x}{dt}=-\Omega V_y\\ \frac{7}{2}\frac{d{V}_y}{dt}=\Omega V_x-\frac{5}{2}g\text{sin}\alpha \end{array}}$

Trayectoria del c.m. de la esfera

Tenemos que resolver un sistema de dos ecuaciones diferenciales acopladas. Para desacoplarlas, despejamos V_y de la primera ecuación y la introducimos en la segunda.

${\displaystyle \frac{d^2{V}_x}{d{t}^2}+\frac{2^2{\Omega }^2}{7^2}{V}_x=\frac{10\Omega }{49}g\text{sin}\alpha }$

La solución de esta ecuación diferencial (similar a la de un MAS) es de la forma

V_x=Acos(k·t)+B·sin(k·t)+c

donde k=2Ω/7

Introduciendo V_x en la ecuación diferencial, obtenemos la solución particular c de la ecuación diferencial de segundo orden.

${\displaystyle V_x=A\cos \left(\frac{2\Omega }{7}·t\right)+B\text{sin}\left(\frac{2\Omega }{7}·t\right)+\frac{5g}{2\Omega }\text{sin}\alpha }$

A partir de la expresión de V_x, obtenemos la componente V_y de la velocidad del c.m.

${\displaystyle V_y=-\frac{7}{2\Omega }\frac{d{V}_x}{dt}=A\text{sin}\left(\frac{2\Omega }{7}·t\right)-B\text{cos}\left(\frac{2\Omega }{7}·t\right)}$

Las constantes A y B se determinan a partir de las condiciones iniciales. En el instante t=0, las componentes de la velocidad del c.m. son (V_0x, V_0y).

${\displaystyle \begin{array}{l}{V}_x=\left(V_{0x}-\frac{5g}{2\Omega }\text{sin}\alpha \right)\cos \left(\frac{2\Omega }{7}·t\right)-V_{0y}\text{sin}\left(\frac{2\Omega }{7}·t\right)+\frac{5g}{2\Omega }\text{sin}\alpha \\ V_y=\left(V_{0x}-\frac{5g}{2\Omega }\text{sin}\alpha \right)\text{sin}\left(\frac{2\Omega }{7}·t\right)+V_{0y}\text{cos}\left(\frac{2\Omega }{7}·t\right)\end{array}}$

Podemos escribir estas ecuaciones de forma general definiendo dos variables, cuyo significado veremos más adelante.

${\displaystyle V_d=\frac{5g}{2\Omega }\text{sin}\alpha {\omega }_c=\frac{2\Omega }{7}}$

V_x=(V_0x-V_d)·cos(ω_ct)-V_0y·sin(ω_c·t)+V_d
V_y=(V_0x-V_d)·sin(ω_ct)+V_0y·cos(ω_c·t)

Sabiendo que en el instante t=0, la posición del centro de la esfera es (x₀, y₀), calculamos la abscisa x del centro de la esfera integrando la expresión de la velocidad V_x en función del tiempo. Se hace lo mismo para la ordenada y.

${\displaystyle \begin{array}{l}x=x_0+\frac{1}{{\omega }_c}\left\{(V_{0x}-V_d\text{)sin(}{\omega }_c·t)+V_{0y}(\text{cos(}{\omega }_c·t)-1)\right\}+V_{d}t\\ y=y_0+\frac{1}{{\omega }_c}\left\{(V_{0x}-V_d)(1-\text{cos(}{\omega }_c·t))+V_{0y}\text{sin(}{\omega }_c·t)\right\}\end{array}}$

Podemos escribir de forma alternativa esta ecuación de la forma

${\displaystyle \begin{array}{l}x-x_0+\frac{V_{0y}}{{\omega }_c}-V_{d}t=\frac{1}{{\omega }_c}\left\{\text{(}{V}_{0x}-V_d\text{)sin(}{\omega }_c·t)+V_{0y}\text{cos(}{\omega }_c·t)\right\}\\ y-y_0-\frac{1}{{\omega }_c}(V_{0x}-V_d)=\frac{1}{{\omega }_c}\left\{-\text{(}{V}_{0x}-V_d\text{)cos(}{\omega }_c·t)+V_{0y}\text{sin(}{\omega }_c·t)\right\}\end{array}}$

Elevando al cuadrado y sumando

${\displaystyle {\left(x-x_0+\frac{V_{0y}}{{\omega }_c}-V_{d}t\right)}^2+{\left(y-y_0-\frac{V_{0x}}{{\omega }_c}+\frac{V_d}{{\omega }_c}\right)}^2=\frac{1}{{\omega }_c^2}\left\{{\left(V_{0x}-V_d\right)}^{\text{2}}+V_{0y}^2\right\}}$

Se trata de la ecuación de una circunferencia centrada en el punto (a, b) y de radio R_c

(x-a)²+(y-b)²=R_c²

donde

${\displaystyle \begin{array}{l}a=x_0-\frac{V_{0y}}{{\omega }_c}+V_{d}tb=y_0+\frac{V_{0x}}{{\omega }_c}-\frac{V_d}{{\omega }_c}\\ R_c=\frac{1}{{\omega }_c}\sqrt{{\left(V_{0x}-V_d\right)}^{\text{2}}+V_{0y}^2}\end{array}}$

El centro se mueve a lo largo del eje X (perpendicular a la dirección de inclinación Y del plano) con velocidad V_d, que se denomina velocidad de deriva.

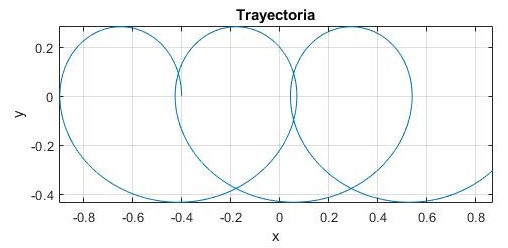
Ejemplo

• Posición inicial de la esfera: y₀=0, x₀=-0.4
• Velocidad inicial de la esfera: V₀=0.2, φ=90º bien, V_0x=0, V_0y=0.2
• Velocidad angular de rotación de la plataforma: Ω=2 rad/s
• Inclinación de la plataforma α=0.2

x0=-0.4; %posición inicial
y0=0;
V0x=0; %velocidad incial
V0y=0.2;
W=2; %velocidad angular de rotación de la plaformsa
alfa=0.2*pi/180; %inclinación

wc=2*W/7; %frecuencia angular
Vd=5*9.8*sin(alfa)/(2*W); %velocidad deriva
x=@(t) x0+((V0x-Vd)*sin(wc*t)+V0y*(cos(wc*t)-1))/wc+Vd*t;
y=@(t) y0+((V0x-Vd)*(1-cos(wc*t))+V0y*sin(wc*t))/wc;
fplot(x,y,[0,10*pi]) %trayectoria
axis equal
xlabel('x')
ylabel('y')
grid on
title('Trayectoria')

Casos particulares

Cuando la plataforma está horizontal α=0

Si la plataforma está horizontal α=0, y V_d=0

La circunferencia está centrada en el punto fijo

${\displaystyle a=x_0-\frac{V_{0y}}{{\omega }_c}b=y_0+\frac{V_{0y}}{{\omega }_c}{R}_c=\frac{V_0}{{\omega }_c}}$

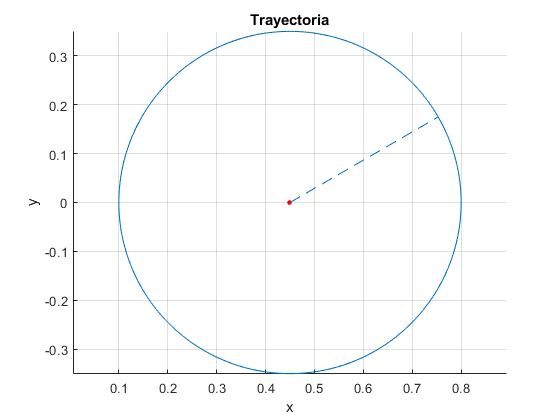
La esfera describe una circunferencia alrededor de un centro que no coincide con el eje de rotación de la plataforma. El tiempo que tarda en dar una vuelta completa es

${\displaystyle \frac{2\pi }{{\omega }_c}=\frac{7}{2}\frac{2\pi }{\Omega }}$

7/2 veces el tiempo que precisa la plataforma en dar una vuelta completa. Así pues, ω_c es la frecuencia angular de la esfera en su movimiento orbital sobre la plataforma giratoria. Como la esfera rueda sin deslizar, no se deberá confundir ω_c con la velocidad angular de rotación de la esfera alrededor de su propio eje

Ejemplo:

• Posición inicial de la esfera y₀=0, x₀=0.8
• Velocidad inicial de la esfera: V₀=0.2, φ=90º bien, V_0x=0, V_0y=0.2
• Velocidad angular de rotación de la plataforma: Ω=2 rad/s
• Inclinación de la plataforma α=0

x0=0.8; %posición inicial
y0=0;
V0x=0; %velocidad incial
V0y=0.2;
W=2; %velocidad angular de rotación de la plaformsa
alfa=0; %inclinación

wc=2*W/7; %frecuencia angular
Vd=5*9.8*sin(alfa)/(2*W); %velocidad deriva
x=@(t) x0+((V0x-Vd)*sin(wc*t)+V0y*(cos(wc*t)-1))/wc+Vd*t;
y=@(t) y0+((V0x-Vd)*(1-cos(wc*t))+V0y*sin(wc*t))/wc;

a=x0-V0y/wc; b=y0*V0y/wc; %centro
Rc=sqrt(V0x^2+V0y^2)/wc; %radio
hold on
fplot(x,y,[0,2*pi/wc]) %trayectoria
plot(a,b,'ro','markersize',3,'markeredgecolor' ,'r','markerfacecolor','r')
line([a,a+Rc*cos(pi/6)],[b,b+Rc*sin(pi/6)],'lineStyle','--')
hold off
axis equal
xlabel('x')
ylabel('y')
grid on
title('Trayectoria')

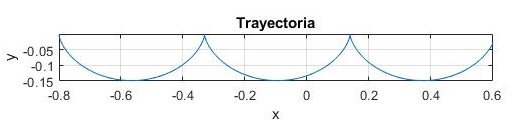
Cuando la esfera parte del reposo

V_0x=V_0y=0 desde el origen x₀=0, y₀=0

${\displaystyle \begin{array}{l}x=\frac{V_d}{{\omega }_c}\left\{\text{-sin}\left({\omega }_c·t\right)+{\omega }_c·t\right\}\\ y=\frac{V_d}{{\omega }_c}\left(-1+\text{cos}\left({\omega }_c·t\right)\right)\end{array}}$

que son las ecuaciones de una cicloide

Ejemplo:

• Posición inicial de la esfera: y₀=0, x₀=-0.8
• Inclinación de la plataforma α=0.2
• Velocidad inicial de la esfera: V₀=0, φ=0º bien,  V_0x=0.0, V_0y=0.0
• Velocidad angular de rotación de la plataforma: Ω=2 rad/s

x0=-0.8;
y0=0;
V0x=0; %velocidad incial
V0y=0;
W=2; %velocidad angular de rotación de la plaformsa
alfa=0.2*pi/180; %inclinación

wc=2*W/7; %frecuencia angular
Vd=5*9.8*sin(alfa)/(2*W); %velocidad deriva
x=@(t) x0+((V0x-Vd)*sin(wc*t)+V0y*(cos(wc*t)-1))/wc+Vd*t;
y=@(t) y0+((V0x-Vd)*(1-cos(wc*t))+V0y*sin(wc*t))/wc;
fplot(x,y,[0,10*pi]) %trayectoria
axis equal
xlabel('x')
ylabel('y')
grid on
title('Trayectoria')

Movimiento rectilíneo

Si V_0y=0, y V_0x=V_d.

x=x₀+V_d·t
y=y₀

La esfera se mueve horizontalmente a lo largo del eje X (no a lo largo del plano inclinado) con velocidad constante.

Ejemplo:

• Posición inicial de la esfera: y₀=0, x₀=-0.8
• Inclinación de la plataforma α=0.2
• Velocidad inicial de la esfera: V₀=5g·sinα/(2Ω), φ=0º bien, V_0x=0.043, V_0y=0.0
• Velocidad angular de rotación de la plataforma: Ω=2 rad/s

x0=-0.8; %posición inicial
y0=0;
V0x=0.043; %velocidad incial
V0y=0;
W=2; %velocidad angular de rotación de la plaformsa
alfa=0.2*pi/180; %inclinación

wc=2*W/7; %frecuencia angular
Vd=5*9.8*sin(alfa)/(2*W); %velocidad deriva
x=@(t) x0+((V0x-Vd)*sin(wc*t)+V0y*(cos(wc*t)-1))/wc+Vd*t;
y=@(t) y0+((V0x-Vd)*(1-cos(wc*t))+V0y*sin(wc*t))/wc;
fplot(x,y,[0,5*pi],'color','r') %trayectoria
axis equal
xlabel('x')
ylabel('y')
grid on
title('Trayectoria')

Actividades

Se introduce

• La posición de partida x₀, en el control titulado Posición. La ordenada se ha fijado en y₀=0.

• La velocidad angular de rotación Ω de la plataforma, en el control titulado Velocidad angular

• La velocidad inicial V₀ de la esfera, en el control titulado Velocidad inicial

• La orientación φ del vector velocidad inicial V₀, en el control titulado Angulo velocidad. Las componentes del vector velocidad son: V_0x=V₀·cosφ, V_0y=V₀·sinφ.

• El ángulo α de inclinación de la plataforma, en el control titulado Inclinación plataforma.

Se pulsa el botón titulado Nuevo

Se observa la trayectoria del centro de la esfera sobre la plataforma horizontal e inclinada.

Referencias

Sambles J. R., Preist T. W., Lang S. R., Toms R. P. A rolling sphere on a tilted rotating turntable. Phys. Educ. 18, (1983), pp. 234-239