Un movimiento ondulatorio armónico se propaga por una cuerda muy larga de densidad μ, cuya tensión es T. La ecuación del movimiento ondulatorio armónico de frecuencia angular ω es

${\displaystyle y(x,t)=A_0\cos \left(kx-\omega t+\phi \right),\omega =kc,c=\sqrt{\frac{T}{\mu }}}$

c es la velocidad de propagación y k=2π/λ es el número de onda, A₀ es la amplitud y φ la fase inicial

Es conveniente expresar la ecuación del movimiento ondulatorio armónico en forma compleja

${\displaystyle \psi (x,t)=A\exp \left(i(kx-\omega t)\right)}$

La amplitud compleja A=A₀exp(iφ), contiene la información de la amplitud y fase. El desplazamiento vertical de la cuerda en la posición x y en el instante t, es la parte real y(x,t)=ReΨ(x,t)

Una cuerda muy larga con una cuenta en el origen

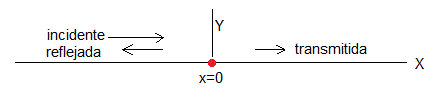
Situamos una bolita de masa m en la posición x=0.

• El movimiento ondulatorio incidente, se propaga de izquierda a derecha, en la región x<0, con A=A₀exp(iφ_a)

${\displaystyle {\psi }_I(x,t)=A\exp \left(i(kx-\omega t)\right)}$

• El movimiento ondulatorio reflejado, se propaga de derecha a izquierda, en la región x<0, con B=B₀exp(iφ_b)

${\displaystyle {\psi }_R(x,t)=B\exp \left(i(-kx-\omega t)\right)}$

• El movimiento ondulatorio transmitido, se propaga de izquierda a derecha, en la región x>0, con C=C₀exp(iφ_c)

${\displaystyle {\psi }_T(x,t)=C\exp \left(i(kx-\omega t)\right)}$

En la región

• x<0, tenemos la superposición de dos movimientos ondulatorios, inicidente y reflejado

${\displaystyle {\psi }_1(x,t)=A\exp \left(i(kx-\omega t)\right)+B\exp \left(i(-kx-\omega t)\right)}$

• x>0, tenemos el movimiento ondulatorio transmitido

${\displaystyle {\psi }_2(x,t)=C\exp \left(i(kx-\omega t)\right)}$

Condiciones en x=0

• La cuerda es continua

${\displaystyle \begin{array}{l}{\psi }_1(\mathrm{0,}t)={\psi }_2(\mathrm{0,}t)\\ A+B=C\end{array}}$

• Estudimos el desplazamianto vertical de la bolita de masa m

Supongamos que la cuerda tiene una tensión T



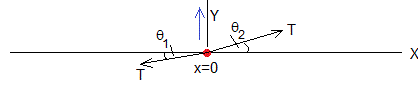
La parte izquierda de la cuerda ejerce una fuerza vertical Tsinθ₁ sobre la bolita. La parte derecha de la cuerda ejerce una fuerza vertical Tsinθ₂ sobre la bolita. La segunda ley de Newton se escribe

${\displaystyle \begin{array}{l}m\frac{{\partial }^{2}y}{\partial t^2}=T\sin {\theta }_2-T\sin {\theta }_1\\ m\frac{{\partial }^2{\psi }_2(\mathrm{0,}t)}{\partial t^2}\approx T\left(\tan {\theta }_2-\tan {\theta }_1\right)=T{\left(\frac{\partial {\psi }_2(x,t)}{\partial x}-\frac{\partial {\psi }_1(x,t)}{\partial x}\right)|}_{x=0}\end{array}}$

Para ángulos θ_1,2 pequeños, hacemos la aproximación, sinθ≈tanθ. Dado que Ψ₁(0,t)=Ψ₂(0,t), la derivada segunda con respecto al tiempo se puede hacer de Ψ₁ o de Ψ₂

${\displaystyle -mC{\omega }^2=ikT\left(C-(A-B)\right)}$

Despejamos los coeficientes complejos B y C en función de A en el sistema de dos ecuaciones

${\displaystyle \begin{array}{l}\{\begin{array}{l}A+B=C\\ -mC{\omega }^2=ikT\left(C-(A-B)\right)\end{array}\\ C=\frac{1}{1-i\alpha }A,B=\frac{i\alpha }{1-i\alpha }A,\alpha =\frac{m{\omega }^2}{2kT}\end{array}}$

El coeficiente complejo B nos proporciona la amplitud y la fase de la onda reflejada y el coeficiente C, la amplitud y la fase de la onda transmitida.

• Representamos el módulo de |B/A| y de |C/A| en función de α

hold on
r=@(x) abs(x*1i./(1-x*1i));
t=@(x) abs(1./(1-x*1i));
fplot(r, [0,5])
fplot(t, [0,5])
hold off
grid on
xlabel('\alpha')
ylabel('r,t')
legend('r','t')
title('Reflexión y transmisión')



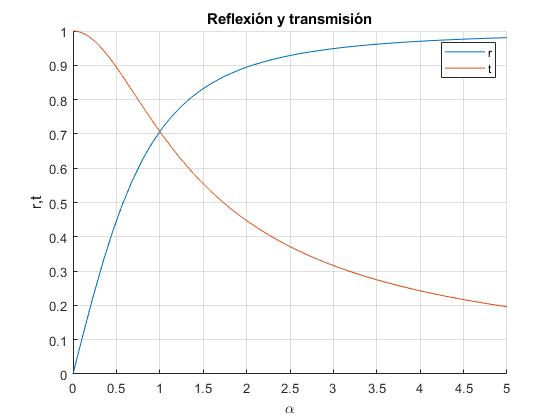
• Representamos la fase de B/A y de C/A en función de α

hold on
r=@(x) angle(x*1i./(1-x*1i));
t=@(x) angle(1./(1-x*1i));
fplot(r, [0,5])
fplot(t, [0,5])
hold off
set(gca,'YTick',0:pi/6:pi)
set(gca,'YTickLabel',{'0','\pi/6','\pi/3','\pi/2','2\pi/3','5\pi/6','\pi'})
grid on
xlabel('\alpha')
ylabel('r,t')
legend('r','t')
title('Reflexión y transmisión')



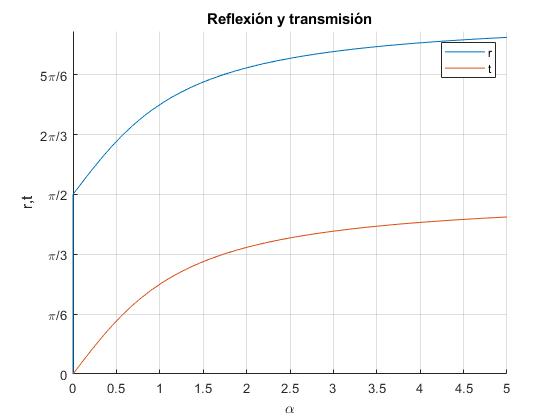
La diferencia de fase entre la onda incidente y reflejada es π/2 cuando α→0. Tiende hacia π cuando α se hace grande, mientras que la onda transmitida tiende hacia π/2

Fuerza horizontal que ejerce el movimiento ondulatorio sobre la partícula

Como los ángulos θ₁ y θ₂ son pequeños, hacemos la aproximación

${\displaystyle \cos \theta =\frac{1}{\sqrt{1+{\tan }^2\theta }}\approx 1-\frac{1}{2}{\tan }^2\theta }$

En el código la variable simbólica x es tanθ

>> syms x;
>> taylor(1/sqrt(1+x^2), x, 'Order',5)
ans =(3*x^4)/8 - x^2/2 + 1

La componente horizontal de la fuerza que ejerce la cuerda sobre la bolita es

${\displaystyle \begin{array}{l}{F}_x=T\cos {\theta }_2-T\cos {\theta }_1\approx T\left(1-\frac{1}{2}{\tan }^2{\theta }_2\right)-T\left(1-\frac{1}{2}{\tan }^2{\theta }_1\right)=\frac{T}{2}\left({\tan }^2{\theta }_1-{\tan }^2{\theta }_2\right)\\ F_x\approx \frac{T}{2}{\left({\left(\frac{\partial y_1(x,t)}{\partial x}\right)}^2-{\left(\frac{\partial y_2(x,t)}{\partial x}\right)}^2\right)|}_{x=0}\end{array}}$

Sabiendo que los desplazamientos y(x,t) de los puntos de la cuerda son la parte real de Ψ₁(x,t) y Ψ₂(x,t)

${\displaystyle \begin{array}{l}{y}_1(x,t)=A_0\cos (kx-\omega t+{\phi }_a)+B_0\cos (-kx-\omega t+{\phi }_b)\\ y_2(x,t)=C_0\cos (kx-\omega t+{\phi }_c)\end{array}}$

La componente horizontal F_x vale

${\displaystyle \begin{array}{l}{F}_x\approx \frac{T}{2}\left\{k^2{\left(-A_0\sin ({\phi }_a-\omega t)+B_0\sin ({\phi }_b-\omega t)\right)}^2-k^2{\left(-C_0\sin ({\phi }_c-\omega t)\right)}^2\right\}\\ F_x\approx k^2\frac{T}{2}\left\{A_0^2{\sin }^2({\phi }_a-\omega t)+B_0^2{\sin }^2({\phi }_b-\omega t)-2A_0{B}_0\sin ({\phi }_a-\omega t)\sin ({\phi }_b-\omega t)-C_0^2{\sin }^2({\phi }_c-\omega t)\right\}\end{array}}$

Calculamos su valor medio durante un perido P=2π/ω de oscilación

${\displaystyle \langle F_x\rangle =k^2\frac{T}{2}\left\{A_0^2\langle {\sin }^2\left({\theta }_a-\omega t\right)\rangle +B_0^2\langle {\sin }^2\left({\theta }_b-\omega t\right)\rangle -2A_0{B}_0\langle \sin \left({\theta }_a-\omega t\right)\sin \left({\theta }_b-\omega t\right)\rangle -C_0^2\langle {\sin }^2\left({\theta }_c-\omega t\right)\rangle \right\}}$

Se define valor medio de una función periódica f(t) de periodo P

${\displaystyle \langle f(t)\rangle =\frac{1}{P}{\displaystyle \underset{0}{\overset{P}{\int }}f(t)·dt}}$

w=1; %frecuencia angular
hold on
fplot(@(t) sin(w*t).^2,[0,pi/w])
fplot(@(t) cos(w*t).^2,[0,pi/w])
fplot(@(t) sin(w*t).*cos(w*t),[0,pi/w])
line([0,pi],[0.5,0.5],'lineStyle','--','color','k')
line([0,pi],[0,0],'lineStyle','--','color','k')
xlabel('t')
ylabel('y')
legend('sin^2','cos^2','sin·cos','location','best')
grid on
title('Funciones periódicas')

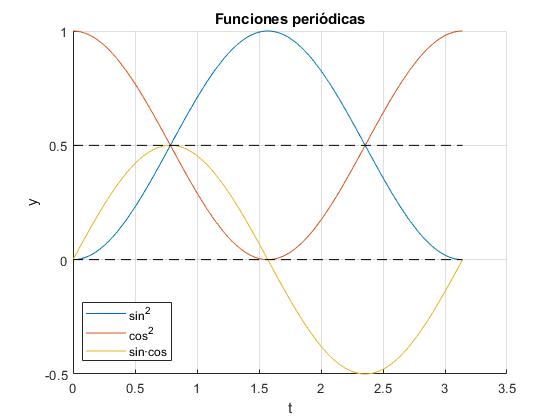
>> syms w t;
>> int(sin(w*t)^2,t,0,pi/w)*w/pi
ans =1/2
>> int(cos(w*t)^2,t,0,pi/w)*w/pi
ans =1/2
>> int(cos(w*t)*sin(w*t),t,0,pi/w)*w/pi
ans =0

Conociendo los valores medios de las funciones periódicas

${\displaystyle \begin{array}{l}\langle {\sin }^2\left(\theta -\omega t\right)\rangle ={\sin }^2\theta \langle {\cos }^2\omega t\rangle +{\cos }^2\theta \langle {\sin }^2\omega t\rangle -\cos \theta \sin \theta \langle \cos \omega t·\sin \omega t\rangle =\frac{1}{2}\\ \langle \sin \left({\theta }_a-\omega t\right)·\sin \left({\theta }_b-\omega t\right)\rangle =\cos {\theta }_a\cos {\theta }_b\langle {\cos }^2\omega t\rangle +\sin {\theta }_a\sin {\theta }_b\langle {\sin }^2\omega t\rangle -\langle \cos \omega t·\sin \omega t\rangle \sin ({\theta }_a+{\theta }_b)=\frac{1}{2}\cos ({\theta }_a-{\theta }_b)\end{array}}$

El resultado es

${\displaystyle \langle F_x\rangle =k^2\frac{T}{4}\left\{A_0^2+B_0^2-2A_0{B}_0\cos ({\theta }_a-{\theta }_b)-C_0^2\right\}}$

Hacemos cero la fase de la onda incidente φ_a=0, y calculamos la parte real e imaginaria de los coeficientes B y C

${\displaystyle \begin{array}{l}B=\frac{i\alpha }{1-i\alpha }{A}_0=\left(\frac{-{\alpha }^2}{1+{\alpha }^2}+i\frac{\alpha }{1+{\alpha }^2}\right)A_0,B_0=\frac{{\alpha }^2}{1+{\alpha }^2}{A}_0\\ C=\left(\frac{1}{1+{\alpha }^2}+i\frac{\alpha }{1+{\alpha }^2}\right)A_0,C_0=\frac{1}{1+{\alpha }^2}{A}_0\end{array}}$

Relacionamos el valor medio de la componente horizontal de la fuerza <F_x> con la frecuencia angular ω

${\displaystyle \begin{array}{l}\langle F_x\rangle =k^2\frac{T}{4}\left\{A_0^2+B_0^2-2A_0\mathrm{Re}(B)-C_0^2\right\}\\ \langle F_x\rangle =k^2\frac{T}{4}\left\{1+\frac{{\alpha }^2}{1+{\alpha }^2}-2\frac{-{\alpha }^2}{1+{\alpha }^2}-\frac{1}{1+{\alpha }^2}\right\}{A}_0^2=k^{2}T\frac{{\alpha }^2}{1+{\alpha }^2}{A}_0^2\\ \langle F_x\rangle =\frac{m^2}{4T}\frac{{\omega }^4}{1+\frac{m^2{\omega }^4}{4\mu T}}\end{array}}$

Una cuerda muy larga con dos cuentas

En la cuerda se han situado dos bolitas en las posiciones x=0 y x=a

• En la región, x<0, tenemos un movimiento ondulatorio incidente y otro reflejado por la primera bolita

${\displaystyle {\psi }_1(x,t)=A\exp \left(i(kx-\omega t)\right)+B\exp \left(i(-kx-\omega t)\right)}$

• En la región, 0<x<a, tenemos un movimiento ondulatorio transmitido y otro reflejado por la segunda bolita

${\displaystyle {\psi }_2(x,t)=C\exp \left(i(kx-\omega t)\right)+D\exp \left(i(-kx-\omega t)\right)}$

• En la región, x>a, tenemos un movimiento ondulotario transmitido

${\displaystyle {\psi }_3(x,t)=E\exp \left(i(kx-\omega t)\right)}$

Condiciones en el x=0 y en x=a

• La cuerda es continua en x=0

${\displaystyle \begin{array}{l}{\psi }_1(\mathrm{0,}t)={\psi }_2(\mathrm{0,}t)\\ A+B=C+D\end{array}}$

• Analizamos el desplazamiento vertical de la bolita situada en x=0

${\displaystyle \begin{array}{l}m\frac{{\partial }^2{\psi }_1(\mathrm{0,}t)}{\partial t^2}=T{\left(\frac{\partial {\psi }_2(x,t)}{\partial x}-\frac{\partial {\psi }_1(x,t)}{\partial x}\right)|}_{x=0}\\ -m{\omega }^2(A+B)=T(ik)(C-D-(A-B))\\ 2i\alpha (A+B)=C-D-A+B\end{array}}$

• La cuerda es continua en x=a

${\displaystyle \begin{array}{l}{\psi }_2(a,t)={\psi }_3(a,t)\\ C{e}^{ika}+D{e}^{-ika}=E{e}^{ika}\end{array}}$

• Analizamos el desplazamiento vertical de la bolita situada en x=a

${\displaystyle \begin{array}{l}m\frac{{\partial }^2{\psi }_3(a,t)}{\partial t^2}=T{\left(\frac{\partial {\psi }_3(x,t)}{\partial x}-\frac{\partial {\psi }_2(x,t)}{\partial x}\right)|}_{x=a}\\ -m{\omega }^{2}E{e}^{ika}=T(ik)(E{e}^{ika}-(C{e}^{ika}-D{e}^{-ika}))\end{array}}$

Despejamos los coeficientes complejos B, C, D y E en función de A en el sistema de cuatro ecuaciones

${\displaystyle \begin{array}{l}\{\begin{array}{l}A+B=C+D\\ 2i\alpha (A+B)=C-D-A+B\\ C{e}^{ika}+D{e}^{-ika}=E{e}^{ika}\\ 2i\alpha E{e}^{ika}=E{e}^{ika}-C{e}^{ika}+D{e}^{-ika}\end{array}\\ \left(\begin{array}{cccc}1& -1& -1& 0\\ 1-2i\alpha & 1& -1& 0\\ 0& e^{ika}& e^{-ika}& -e^{ika}\\ 0& -e^{ika}& e^{-ika}& (1-2i\alpha )e^{ika}\end{array}\right)\left(\begin{array}{c}B\\ C\\ D\\ E\end{array}\right)=A\left(\begin{array}{c}-1\\ 1+2i\alpha \\ 0\\ 0\end{array}\right)\\ B=\frac{\alpha \left(\alpha (1-e^{2ika})+i(1+e^{2ika})\right)}{1-2i\alpha -{\alpha }^2(1-e^{2ika})}A\\ C=\frac{1-i\alpha }{1-2i\alpha -{\alpha }^2(1-e^{2ika})}A\\ D=\frac{i\alpha e^{2ika}}{1-2i\alpha -{\alpha }^2(1-e^{2ika})}A\\ E=\frac{1}{1-2i\alpha -{\alpha }^2(1-e^{2ika})}A\end{array}}$

Utilizamos el operador \ división por la izquierda para resolver el sistema de ecuaciones

En el código MATLAB la variable simbólica x representa al parámetro α,

>> syms x a k;
A=[1,-1,-1,0;1-2*1i*x,1,-1,0;0, exp(1i*k*a),exp(-1i*k*a), -exp(1i*k*a); 
0,-exp(1i*k*a),exp(-1i*k*a),(1-2*1i*x)*exp(1i*k*a)];
B=[-1;1+2*1i*x;0;0];
X=A\B;

El coeficiente complejo B nos proporciona la amplitud y la fase de la onda reflejada y el coeficiente E, la amplitud y la fase de la onda transmitida.

Representamos el módulo de |B/A| y de |E/A| en función de α, para ka=0.5

ka=0.5;
hold on
t=@(x) abs(1./(1-2*x*1i-x.^2*(1-exp(2*1i*ka))));
r=@(x) abs(x.*(x*(1-exp(2*1i*ka))+1i*(1+exp(2*1i*ka))).
/(1-2*x*1i-x.^2*(1-exp(2*1i*ka))));
fplot(r, [0,4])
fplot(t, [0,4])
hold off
grid on
xlabel('\alpha')
ylabel('r,t')
legend('r','t')
title('Reflexión y transmisión')

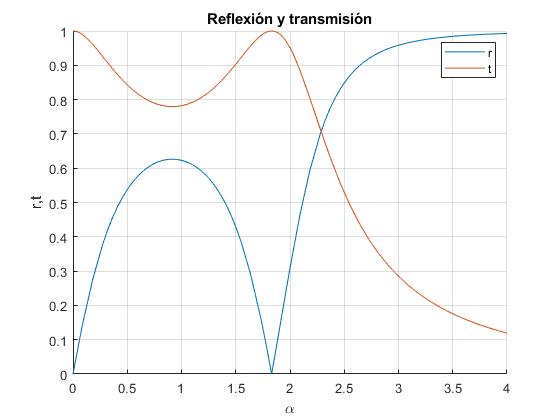
El módulo |B/A| se anula cuando el numerador de B sea nulo

${\displaystyle \begin{array}{l}{e}^{2ika}=\frac{\alpha +i}{\alpha -i}\\ \cos (2ka)=\frac{{\alpha }^2-1}{{\alpha }^2+1}\end{array}}$

Cuando ka=0.5, α=1.8305

Sustituyendo el comando abs por angle, representamos las fases de la onda reflejada y transmitida que tienen un comportamiento complejo

Fuerza horizontal que ejerce el movimiento ondulatorio sobre cada una de las bolitas

Realizamos operaciones semejantes al primer apartado para calcular la componente horizontal F₁ y F₂ de las fuerzas que ejerce la cuerda sobre cada una de las bolitas

• Sobre la bolita situada en x=0

Los desplazamientos verticales de la cuerda en las regiones x<0 y 0<x<a son

${\displaystyle \begin{array}{l}{y}_1(x,t)=A_0\cos (kx-\omega t+{\theta }_a)+B_0\cos (-kx-\omega t+{\theta }_b)\\ y_2(x,t)=C_0\cos (-kx-\omega t+{\theta }_c)+D_0\cos (kx-\omega t+{\theta }_d)\end{array}}$

La fuerza horizontal F₁ y su valor medio valen

${\displaystyle \begin{array}{l}{F}_1\approx \frac{T}{2}{\left({\left(\frac{\partial y_1(x,t)}{\partial x}\right)}^2-{\left(\frac{\partial y_2(x,t)}{\partial x}\right)}^2\right)|}_{x=0}\\ F_1\approx \frac{T}{2}\left\{k^2{\left(-A_0\sin ({\theta }_a-\omega t)+B_0\sin ({\theta }_b-\omega t)\right)}^2-k^2{\left(-C_0\sin ({\theta }_c-\omega t)+D_0\sin ({\theta }_d-\omega t)\right)}^2\right\}\\ F_1\approx k^2\frac{T}{2}\left\{\begin{array}{l}{A}_0^2{\sin }^2({\theta }_a-\omega t)+B_0^2{\sin }^2({\theta }_b-\omega t)-2A_0{B}_0\sin ({\theta }_a-\omega t)\sin ({\theta }_b-\omega t)\\ -C_0^2{\sin }^2({\theta }_c-\omega t)-D_0^2{\sin }^2({\theta }_d-\omega t)+2C_0{D}_0\sin ({\theta }_c-\omega t)\sin ({\theta }_d-\omega t)\end{array}\right\}\\ \langle F_1\rangle =k^2\frac{T}{2}\left\{\begin{array}{l}{A}_0^2\langle {\sin }^2\left({\theta }_a-\omega t\right)\rangle +B_0^2\langle {\sin }^2\left({\theta }_b-\omega t\right)\rangle -2A_0{B}_0\langle \sin \left({\theta }_a-\omega t\right)\sin \left({\theta }_b-\omega t\right)\rangle \\ -C_0^2\langle {\sin }^2\left({\theta }_c-\omega t\right)\rangle -D_0^2\langle {\sin }^2\left({\theta }_d-\omega t\right)\rangle +2C_0{D}_0\langle \sin \left({\theta }_c-\omega t\right)\sin \left({\theta }_d-\omega t\right)\rangle \end{array}\right\}\\ \langle F_1\rangle =k^2\frac{T}{2}\left\{\frac{1}{2}{A}_0^2+\frac{1}{2}{B}_0^2-A_0{B}_0\cos ({\theta }_a-{\theta }_b)-\frac{1}{2}{C}_0^2-\frac{1}{2}{D}_0^2+C_0{D}_0\cos ({\theta }_c-{\theta }_d)\right\}\\ \langle F_1\rangle =k^2\frac{T}{2}\left\{\frac{1}{2}{A}_0^2+\frac{1}{2}{B}_0^2-A_0\mathrm{Re}(B)-\frac{1}{2}{C}_0^2-\frac{1}{2}{D}_0^2+\left(\mathrm{Re}(C)\mathrm{Re}(D)+\mathrm{Im}(C)\mathrm{Im}(D)\right)\right\}\end{array}}$

• Sobre la bolita situada en x=a

Los desplazamientos verticales de la cuerda en las regiones 0<x<a y x>a son

${\displaystyle \begin{array}{l}{y}_2(x,t)=C_0\cos (kx-\omega t+{\theta }_c)+D_0\cos (-kx-\omega t+{\theta }_d)\\ y_3(x,t)=E_0\cos (kx-\omega t+{\theta }_e)\end{array}}$

La fuerza horizontal F₂ y su valor medio valen

${\displaystyle \begin{array}{l}{F}_2\approx \frac{T}{2}{\left({\left(\frac{\partial y_2(x,t)}{\partial x}\right)}^2-{\left(\frac{\partial y_3(x,t)}{\partial x}\right)}^2\right)|}_{x=a}\\ F_2\approx \frac{T}{2}\left\{k^2{\left(-C_0\sin (ka+{\theta }_c-\omega t)+D_0\sin (-ka+{\theta }_d-\omega t)\right)}^2-k^2{\left(-E_0\sin (ka+{\theta }_e-\omega t)\right)}^2\right\}\\ F_2\approx k^2\frac{T}{2}\left\{\begin{array}{l}{C}_0^2{\sin }^2(ka+{\theta }_c-\omega t)+D_0^2{\sin }^2(-ka+{\theta }_d-\omega t)\\ -2C_0{D}_0\sin (ka+{\theta }_c-\omega t)\sin (-ka+{\theta }_d-\omega t)-E_0^2{\sin }^2(ka+{\theta }_e-\omega t)\end{array}\right\}\\ \langle F_2\rangle =k^2\frac{T}{2}\left\{\begin{array}{l}{C}_0^2\langle {\sin }^2\left(ka+{\theta }_c-\omega t\right)\rangle +D_0^2\langle {\sin }^2\left(-ka+{\theta }_d-\omega t\right)\rangle \\ -2C_0{D}_0\langle \sin \left(ka+{\theta }_c-\omega t\right)\sin \left(-ka+{\theta }_d-\omega t\right)\rangle -E_0^2\langle {\sin }^2\left(ka+{\theta }_c-\omega t\right)\rangle \end{array}\right\}\\ \langle F_2\rangle =k^2\frac{T}{2}\left\{\frac{1}{2}{C}_0^2+\frac{1}{2}{D}_0^2-C_0{D}_0\cos (2ka+{\theta }_c-{\theta }_d)-\frac{1}{2}{E}_0^2\right\}\\ \langle F_2\rangle =k^2\frac{T}{2}\left\{\begin{array}{l}\frac{1}{2}{C}_0^2+\frac{1}{2}{D}_0^2-\frac{1}{2}{E}_0^2-\cos (2ka)\left(\mathrm{Re}(C)\mathrm{Re}(D)+\mathrm{Im}(C)\mathrm{Im}(D)\right)+\\ \sin (2ka)\left(\mathrm{Im}(C)\mathrm{Re}(D)-\mathrm{Im}(D)\mathrm{Re}(C)\right)\end{array}\right\}\end{array}}$

El primer paso, es expresar cada coeficiente, por ejemplo, el B de la forma B=Re(B)+i·Im(B), lo que da unas expresiones muy largas para reproducirlas en esta página. El segundo paso, es utilizar Math Symbolic de MATLAB para realizar las operaciones, la parte real e imaginaria del número complejo B se guardan en el vector B, la real en B(1) y la imaginaria en B(2) y así, con los otros coeficientes C, D y E. En el script la variable simbólica x representa el parámetro α

syms x a k;
d=(1-x^2+x^2*cos(2*k*a))^2+(-2*x+x^2*sin(2*k*a))^2; %denominador
B=[(x-x*cos(2*k*a)-sin(2*k*a))*(1-x^2+x^2*cos(2*k*a))+
(-x*sin(2*k*a)+1+cos(2*k*a))*(-2*x+x^2*sin(2*k*a)), -(x-x*cos(2*k*a)-sin(2*k*a))
*(-2*x+x^2*sin(2*k*a))+(-x*sin(2*k*a)+1+cos(2*k*a))*(1-x^2+x^2*cos(2*k*a))]*x/d;
C=[(1-x^2+x^2*cos(2*k*a))-x*(-2*x+x^2*sin(2*k*a)), -(-2*x+x^2*sin(2*k*a))
-x*(1-x^2+x^2*cos(2*k*a))]/d;
D=[-sin(2*k*a)*(1-x^2+x^2*cos(2*k*a))+cos(2*k*a)*(-2*x+x^2*sin(2*k*a)),
 sin(2*k*a)*(-2*x+x^2*sin(2*k*a))+cos(2*k*a)*(1-x^2+x^2*cos(2*k*a))]*(x/d);
E=[(1-x^2+x^2*cos(2*k*a)),-(-2*x+x^2*sin(2*k*a))]/d;
%valores medio de las fuerzas    
F1=1/2+(B(1)^2+B(2)^2)/2-B(1)-(C(1)^2+C(2)^2)/2-(D(1)^2+D(2)^2)/2+
C(1)*D(1)+C(2)*D(2);
F2=(C(1)^2+C(2)^2)/2+(D(1)^2+D(2)^2)/2-(E(1)^2+E(2)^2)/2-(cos(k*a)^2-
sin(k*a)^2)*(C(1)*D(1)+C(2)*D(2))+2*sin(k*a)*cos(k*a)*(C(2)*D(1)-D(2)*C(1));

>> latex(simplify(F1))
ans ='\frac{2\,x^2\,\left(2\,\cos\left(2\,a\,k\right)-4\,x\,\sin\left(2\,a\,k\
right)-2\,x^2\,\cos\left(2\,a\,k\right)+2\,x^2+1\right)}
{2\,x^2\,\cos\left(2\,a\,k\right)-2\,x^4\,\cos\left(2\,a\,k\right)-4\
,x^3\,\sin\left(2\,a\,k\right)+2\,x^2+2\,x^4+1}'

Con simplify, simplificamos las variables F1 y F2, utilizamos el comando latex para copiar la salida y pegarla en MathType, vemos dos fracciones, la primera corresponde a F1 (se muestra en el cuadro anterior) y la segunda a F2

${\displaystyle \begin{array}{l}\frac{2x^2\left(2\cos \left(2ak\right)-4x\sin \left(2ak\right)-2x^2\cos \left(2ak\right)+2x^2+1\right)}{2x^2\cos \left(2ak\right)-2x^4\cos \left(2ak\right)-4x^3\sin \left(2ak\right)+2x^2+2x^4+1}\\ \frac{2x^2}{2x^2\cos \left(2ak\right)-2x^4\cos \left(2ak\right)-4x^3\sin \left(2ak\right)+2x^2+2x^4+1}\end{array}}$

Procedemos a pulir manualmente las dos fracciones, obteniendo

${\displaystyle \begin{array}{l}\langle F_1\rangle =k^{2}T\frac{4{\alpha }^2{\left(\cos (ka)-\alpha \sin (ka)\right)}^2-{\alpha }^2}{4{\alpha }^2{\left(\cos (ka)-\alpha \sin (ka)\right)}^2+1}{A}_0^2\\ \langle F_2\rangle =k^{2}T\frac{{\alpha }^2}{4{\alpha }^2{\left(\cos (ka)-\alpha \sin (ka)\right)}^2+1}{A}_0^2\end{array}}$

Fuerza de Casimir

El efecto Casimir es un fenómeno de Electrodinámica Cuántica, su análogo mecánico se define la fuerza

${\displaystyle \langle F_c\rangle =\frac{1}{2}\langle F_1-F_2\rangle =\frac{k^{2}T}{2}\frac{4{\alpha }^2{\left(\cos (ka)-\alpha \sin (ka)\right)}^2-2{\alpha }^2}{4{\alpha }^2{\left(\cos (ka)-\alpha \sin (ka)\right)}^2+1}{A}_0^2}$

Expresamos esta fuerza en términos de variables adimensionales

${\displaystyle \begin{array}{l}z=ka=\frac{\omega }{c}a=\omega a\sqrt{\frac{\mu }{T}}\\ \beta =\frac{m}{\mu a}\end{array}}$

β es el cociente entre la masa de las cuentas dividido por la masa de la cuerda entre las cuentas. El parámetro α se expresa

${\displaystyle \alpha =\frac{m{\omega }^2}{2kT}=\frac{m{\omega }^2}{2\frac{\omega }{c}T}=\frac{m{c}^2\frac{z}{a}}{2T}=\frac{mz}{2\mu a}=\frac{1}{2}\beta z}$

La fuerza de Casimir se expresa en términos de las variables adimiensionales β y z

${\displaystyle \begin{array}{l}\langle F_c\rangle =\frac{k^{2}T}{2}\frac{{\beta }^2{z}^2{\left(\cos z-\frac{1}{2}\beta z\sin z\right)}^2-\frac{1}{2}{\beta }^2{z}^2}{{\beta }^2{z}^2{\left(\cos z-\frac{1}{2}\beta z\sin z\right)}^2+1}{A}_0^2\\ \frac{\langle F_c\rangle }{T}=\frac{1}{2}\frac{A_0^2}{a^2}{z}^2\frac{{\left(\cos z-\frac{1}{2}\beta z\sin z\right)}^2-\frac{1}{2}}{{\left(\cos z-\frac{1}{2}\beta z\sin z\right)}^2+\frac{1}{{\beta }^2{z}^2}}\end{array}}$

• Si βz es grande la fuerza tiende a

${\displaystyle \frac{\langle F_c\rangle }{T}\approx \frac{1}{2}\frac{A_0^2}{a^2}{z}^2}$

• Si βz es pequeño

Desarrollamos en serie, identificando la variable simbólica a como cosz, la variable simbólica b como sinz/2 y la variable simbólica x como βz

>> syms a b x;
>> y=((a-b*x)^2-1/2)/((a-b*x)^2+1/x^2);
>> taylor(y,x,'Order',4)
ans =x^2*(a^2 - 1/2) - 2*a*b*x^3

${\displaystyle \frac{\langle F_c\rangle }{T}\approx \frac{1}{2}\frac{A_0^2}{a^2}{z}^2{\left(\beta z\right)}^2\left({\cos }^{2}z-\frac{1}{2}\right)=\frac{1}{4}\frac{A_0^2}{a^2}{\beta }^2{z}^4\cos (2z)}$

Representamos el valor medio de la fuerza <F_c(β,z)>, para dos valores de β, uno grande y otro pequeño

hold on
for beta=[0.05,5]
    f=@(z) z.^2.*((cos(z)-beta*z.*sin(z)/2).^2-1/2)./
((cos(z)-beta*z.*sin(z)/2).^2+1./(beta^2*z.^2));
    fplot(f,[0,25])
end
hold off
ylim([-1500,500])
grid on
legend('0.05','5','location','best')
xlabel('z')
ylabel('<F_c>')
title('Interacción entre dos cuentas')

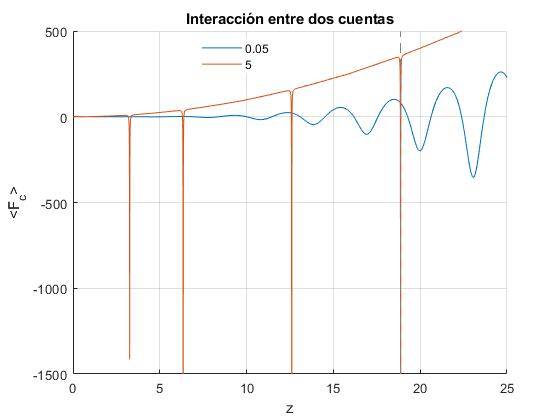
Para el valor grande, observamos valores de z (frecuencia angular ω) para los cuales la fuerza <F_c> es negativa

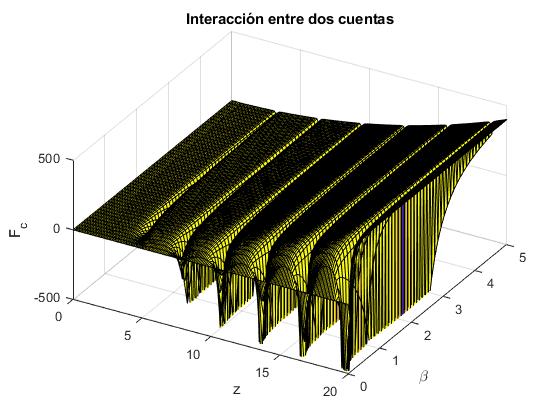
Hacemos una representación tridimensional de la función <F_c(β,z)>

[z,beta]=meshgrid(0:0.1:20,0:0.1:5);
Fc=z.^2.*((cos(z)-beta.*z.*sin(z)/2).^2-1/2)./
((cos(z)-beta.*z.*sin(z)/2).^2+1./(beta.^2.*z.^2));
surf(z,beta,Fc)
xlabel('z')
ylabel('\beta')
zlabel('F_c')
zlim([-500,500])
title('Interacción entre dos cuentas')
view(30,47)

Referencias

David J. Griffiths, Elan Ho. Classical Casimir effect for beads on a string. Am. J. Phys. 69 (11), November 2001, pp. 1173-1176