En la página titulada Propagación de ondas electromagnéticas. Ecuaciones de Fresnel. en el apartado 'Ecuaciones de Maxwell' llegamos a las siguientes expresiones para el campo eléctrico y para el campo magnético

${\displaystyle \begin{array}{l}{\nabla }^2\overrightarrow{E}-\epsilon \mu \frac{{\partial }^2\overrightarrow{E}}{\partial t^2}=\frac{1}{\epsilon }\overrightarrow{\nabla }{\rho }_f+\mu \frac{\partial \overrightarrow{J_f}}{\partial t}\\ {\nabla }^2\overrightarrow{B}-\epsilon \mu \frac{{\partial }^2\overrightarrow{B}}{\partial t^2}=-\mu \overrightarrow{\nabla }\times \overrightarrow{J_f}\end{array}}$

En un medio conductor aplicamos la ley de Ohm $\overrightarrow{J_f}=\sigma \overrightarrow{E}$. Si además, no hay cargas libres ρ_f=0. La ecuación del campo eléctrico se convierte en

${\displaystyle \begin{array}{l}{\nabla }^2\overrightarrow{E}-\epsilon \mu \frac{{\partial }^2\overrightarrow{E}}{\partial t^2}=\sigma \mu \frac{\partial \overrightarrow{E}}{\partial t}\\ {\nabla }^2\overrightarrow{E}-\sigma \mu \frac{\partial \overrightarrow{E}}{\partial t}-\epsilon \mu \frac{{\partial }^2\overrightarrow{E}}{\partial t^2}=0\end{array}}$

Aplicando la ley de Ohm y la ley de Faraday $\overrightarrow{\nabla }\times \overrightarrow{E}+\frac{\partial \overrightarrow{B}}{\partial t}=0$, la ecuación del campo magnético se convierte en

${\displaystyle \begin{array}{l}{\nabla }^2\overrightarrow{B}-\epsilon \mu \frac{{\partial }^2\overrightarrow{B}}{\partial t^2}=-\sigma \mu \overrightarrow{\nabla }\times \overrightarrow{E}\\ {\nabla }^2\overrightarrow{B}-\sigma \mu \frac{\partial B}{\partial t}-\epsilon \mu \frac{{\partial }^2\overrightarrow{B}}{\partial t^2}=0\end{array}}$

Consideremos una onda electromagnética plana, polarizada, que se propaga a lo largo del eje Z, el campo eléctrico

${\displaystyle \overrightarrow{E}=E_0\exp \left(i\left(kz-\omega t\right)\right)\widehat{i}}$

Nota: no confundir la unidad imaginaria $i=\sqrt{-1}$, con el vector unitario en la dirección X, $\widehat{i}$

Se introduce en la ecuación diferencial del campo eléctrico

${\displaystyle \begin{array}{l}(ik)(ik)E_0\exp \left(i\left(kz-\omega t\right)\right)-\sigma \mu (-i\omega )E_0\exp \left(i\left(kz-\omega t\right)\right)-\epsilon \mu (-i\omega )(-i\omega )E_0\exp \left(i\left(kz-\omega t\right)\right)=0\\ -k^2+i\sigma \mu \omega +\epsilon \mu {\omega }^2=0\end{array}}$

k² es un número complejo tal que k=a+ib. Calculamos la parte imaginaria b

${\displaystyle \begin{array}{l}{\left(a+ib\right)}^2=\epsilon \mu {\omega }^2+i\sigma \mu \omega \\ a^2-b^2+2iab=\epsilon \mu {\omega }^2-i\sigma \mu \omega ,\{\begin{array}{l}{a}^2-b^2=\epsilon \mu {\omega }^2\\ 2ab=\sigma \mu \omega \end{array}\\ a=\frac{\sigma \mu \omega }{2b}\\ \frac{{\left(\sigma \mu \omega \right)}^2}{4b^2}-b^2=\epsilon \mu {\omega }^2\\ b^4+\epsilon \mu {\omega }^2{b}^2-{\left(\frac{\sigma \mu \omega }{2}\right)}^2=0\\ b^2=\frac{-\epsilon \mu {\omega }^2\pm \sqrt{{\left(\epsilon \mu {\omega }^2\right)}^2+{\left(\sigma \mu \omega \right)}^2}}{2}\\ b^2=\mu \omega \frac{\sqrt{{\epsilon }^2{\omega }^2+{\sigma }^2}-\epsilon \omega }{2}=\mu \omega \frac{\epsilon \omega }{2}\left(\sqrt{1+{\left(\frac{\sigma }{\epsilon \omega }\right)}^2}-1\right)\\ b=\omega \sqrt{\frac{\epsilon \mu }{2}\left(\sqrt{1+{\left(\frac{\sigma }{\epsilon \omega }\right)}^2}-1\right)}\end{array}}$

Calculamos la parte real a

${\displaystyle \begin{array}{l}b=\frac{\sigma \mu \omega }{2a}\\ a^2-\frac{{\left(\sigma \mu \omega \right)}^2}{4a^2}=\epsilon \mu {\omega }^2\\ a^4-\epsilon \mu {\omega }^2{a}^2-{\left(\frac{\sigma \mu \omega }{2}\right)}^2=0\\ a^2=\frac{\epsilon \mu {\omega }^2\pm \sqrt{{\left(\epsilon \mu {\omega }^2\right)}^2+{\left(\sigma \mu \omega \right)}^2}}{2}\\ a^2=\mu \omega \frac{\sqrt{{\epsilon }^2{\omega }^2+{\sigma }^2}-\epsilon \omega }{2}=\mu \omega \frac{\epsilon \omega }{2}\left(\sqrt{1+{\left(\frac{\sigma }{\epsilon \omega }\right)}^2}+1\right)\\ a=\omega \sqrt{\frac{\epsilon \mu }{2}\left(\sqrt{1+{\left(\frac{\sigma }{\epsilon \omega }\right)}^2}+1\right)}\end{array}}$

Comprobamos que $2ab=\sigma \mu \omega$

Podemos expresar k de dos formas distintas

${\displaystyle \begin{array}{l}k=a+ib\\ k=\sqrt{a^2+b^2}\exp \left(i\Omega \right),\tan \Omega =\frac{b}{a}\end{array}}$

La expresión del vector campo eléctrico es

${\displaystyle \overrightarrow{E}=E_0\exp \left(i\left(kz-\omega t\right)\right)\widehat{i}=E_0\exp \left(i\left(\left(a+bi\right)z-\omega t\right)\right)\widehat{i}=E_0\exp \left(-bz\right)\left(i\left(az-\omega t\right)\right)\widehat{i}}$

Las ondas electromagnéticas constan de una campo eléctrico y un campo magnético perpendiculares entre sí y a la dirección de propagación $\overrightarrow{E}\times \overrightarrow{H}$, si el campo eléctrico tiene la dirección del eje X, el campo magnético tiene la dirección del eje Y

${\displaystyle \overrightarrow{H}=H_0\exp \left(i\left(\omega t-kz\right)\right)\widehat{j}}$

Como vamos a comprobar utilizando la ley de Faraday

${\displaystyle \begin{array}{l}\overrightarrow{\nabla }\times \overrightarrow{E}+\mu \frac{\partial \overrightarrow{H}}{\partial t}=0\\ \left|\begin{array}{ccc}\widehat{i}& \widehat{j}& \widehat{k}\\ \frac{\partial }{\partial x}& \frac{\partial }{\partial y}& \frac{\partial }{\partial z}\\ E_0\exp \left(i\left(kz-\omega t\right)\right)& 0& 0\end{array}\right|+\mu \frac{\partial \overrightarrow{H}}{\partial t}=0\\ -ki{E}_0\widehat{j}+\mu i\omega H_0\widehat{j}=0\\ H_0=E_0\frac{k}{\omega \mu }\end{array}}$

La expresión del vector campo magnético es

${\displaystyle \[ \overrightarrow{H}=E_0\frac{\sqrt{a^2+b^2}\exp \left(i\Omega \right)}{\omega \mu }\exp \left(i\left(\left(a+ib\right)z-\omega t\right)\right)\widehat{j}=\frac{E_0\sqrt{a^2+b^2}}{\omega \mu }\exp \left(-bz\right)\exp \left(i\left(az-\omega t+\Omega \right)\right)\widehat{j} \]}$

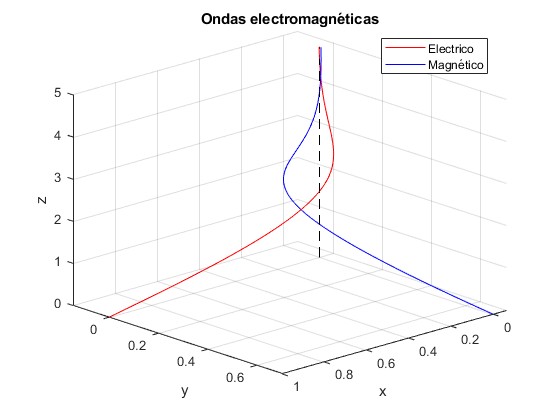
La amplitud del campo eléctrico y del campo magnético decrece exponencialmente con z, exp(-bz). Por otra parte, hay una diferencia de fase Ω entre el campo eléctrico y el campo magnético.

Buenos conductores

Para un buen conductor la conductividad σ/(ωε)>>1

${\displaystyle \begin{array}{l}a=b=\sqrt{\frac{\sigma \mu \omega }{2}},\Omega =\frac{\pi }{4}\\ k=\sqrt{\frac{\sigma \mu \omega }{2}}\left(1+i\right)\end{array}}$

Como la amplitud del campo eléctrico y del campo magnético decrece exponencialmente con z. Se denomina longitud de atenuación δ

${\displaystyle \begin{array}{l}\delta =\frac{1}{b}=\sqrt{\frac{2}{\sigma \mu \omega }}\\ k=\frac{1}{\delta }\left(1+i\right)\end{array}}$

La conductividad del cobre es σ=5.80·10⁷ S/m, a la frecuencia de f=10⁶ Hz. Sabiendo que ω=2πf

${\displaystyle \delta =\sqrt{\frac{2}{2\pi ·{10}^6·4\pi ·{10}^{-7}·5.8·{10}^7}}=0.661·{10}^{-6}\text{m}}$

La inversa 1/δ es un número muy grande, por lo que las ondas de alta frecuencia se atenuan rápidamente. Para un buen conductor k es un número complejo muy grande. La diferencia de fase entre el campo eléctrico y el campo magnético es Ω=π/4

Las partes real del vector campo eléctrico y del vector campo magnético son

${\displaystyle \begin{array}{l}\overrightarrow{E}=E_0\exp \left(-\frac{z}{\delta }\right)\exp \left(i\left(\frac{z}{\delta }-\omega t\right)\right)\widehat{i},\overrightarrow{E}=E_0\exp \left(-\frac{z}{\delta }\right)\cos \left(\frac{z}{\delta }-\omega t\right)\widehat{i}\\ \overrightarrow{H}=\frac{E_0\sqrt{2}}{\delta \omega \mu }\exp \left(-\frac{z}{\delta }\right)\exp \left(i\left(\frac{z}{\delta }-\omega t+\frac{\pi }{4}\right)\right)\widehat{j},\overrightarrow{H}=E_0\sqrt{\frac{\sigma }{\omega \mu }}\exp \left(-\frac{z}{\delta }\right)\cos \left(\frac{z}{\delta }-\omega t+\frac{\pi }{4}\right)\widehat{j}\end{array}}$

z=linspace(0,5,200);
xx=zeros(1,length(z));
hold on
plot3(exp(-z).*cos(z), xx,z,'r')
plot3(xx, exp(-z).*cos(z+pi/4),z,'b')
line([0,0],[0,0],[0,5],'color','k','lineStyle','--')
hold off
grid on
xlabel('x')
ylabel('y')
zlabel('z')
legend('Electrico','Magnético','Location', 'best')
title('Ondas electromagnéticas')
view(137,24)

Reflexión y refracción

Supongamos dos medios no magnéticos, semiinfinitos, lineales, homogéneos e isótropos. Una onda electromagnética que se propaga en el medio 1 (dieléctrico) incide sobre la superficie de separación de los medios 1 y 2 (buen conductor) produciendo una onda reflejada y otra transmitida. Los vectores unitarios ${\widehat{n}}_i$ , ${\widehat{n}}_r$ y ${\widehat{n}}_t$ son normales a los frentes de onda planos (formados por los vectores $\overrightarrow{E}$ y $\overrightarrow{H}$) y tienen el sentido de la propagación $\overrightarrow{E}\times \overrightarrow{H}$ que es el eje Z

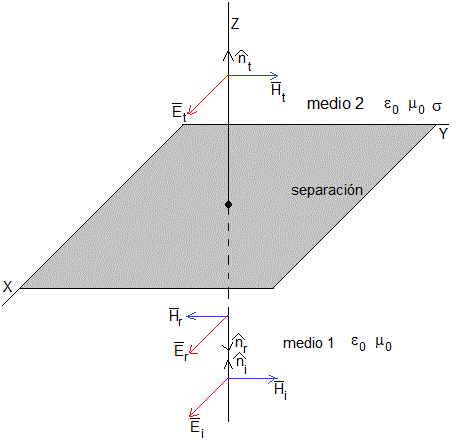
La onda incidente en el medio dieléctrico, ε₀, μ₀, es

${\displaystyle \begin{array}{l}{\overrightarrow{E}}_i=E_{0i}\exp \left(i\left(k_{1}z-\omega t\right)\right)\widehat{i}\\ {\overrightarrow{H}}_i=H_{0i}\exp \left(i\left(k_{1}z-\omega t\right)\right)\widehat{j},H_{0i}=\sqrt{\frac{{\epsilon }_0}{{\mu }_0}}{E}_{0i}\\ k_1=\frac{\omega }{c}=\omega \sqrt{{\epsilon }_0{\mu }_0}\end{array}}$

La onda reflejada en dicho medio

${\displaystyle \begin{array}{l}{\overrightarrow{E}}_r=E_{0r}\exp \left(i\left(k_{1}z+\omega t\right)\right)\widehat{i}\\ {\overrightarrow{H}}_r=-H_{0r}\exp \left(i\left(k_{1}z+\omega t\right)\right)\widehat{j},H_{0r}=\sqrt{\frac{{\epsilon }_0}{{\mu }_0}}{E}_{0r}\end{array}}$

La onda transmitida al medio conductor, ε₀, μ₀, σ≠0

${\displaystyle \begin{array}{l}{\overrightarrow{E}}_t=E_{0t}\exp \left(i\left(k_{2}z-\omega t\right)\right)\widehat{i}\\ {\overrightarrow{H}}_r=H_{0t}\exp \left(i\left(k_{2}z-\omega t\right)\right)\widehat{j},H_{0t}=E_{0t}\frac{k_2}{\omega {\mu }_0}\\ k_2=\omega \sqrt{\frac{{\epsilon }_0{\mu }_0}{2}\left(\sqrt{1+{\left(\frac{\sigma }{{\epsilon }_0{\mu }_0}\right)}^2}+1\right)}+i\omega \sqrt{\frac{{\epsilon }_0{\mu }_0}{2}\left(\sqrt{1+{\left(\frac{\sigma }{{\epsilon }_0{\mu }_0}\right)}^2}-1\right)}\\ k_2=\omega \sqrt{\frac{{\epsilon }_0{\mu }_0}{2}\left(\sqrt{1+{\alpha }^2}+1\right)}+i\omega \sqrt{\frac{{\epsilon }_0{\mu }_0}{2}\left(\sqrt{1+{\alpha }^2}-1\right)}\end{array}}$

En la superficie de separación, las componentes tangenciales de $\overrightarrow{E}$ Y $\overrightarrow{H}$ son continuas (véase el apartado Ecuaciones de Fresnel)

${\displaystyle \{\begin{array}{l}{E}_{0i}+E_{0r}=E_{0t}\\ H_{0i}-H_{0r}=H_{0t}\end{array}}$

Despejamos el cociente E_0t/E_0i del sistema de dos ecuaciones

${\displaystyle \begin{array}{l}\begin{array}{l}\{\begin{array}{l}{E}_{0i}+E_{0r}=E_{0t}\\ \sqrt{\frac{{\epsilon }_0}{{\mu }_0}}\left(E_{0i}-E_{0r}\right)=\frac{k_2}{\omega {\mu }_0}{E}_{0t}\end{array}\hfill \\ 2E_{0i}=\left(1+\frac{k_2}{\omega {\mu }_0}\sqrt{\frac{{\mu }_0}{{\epsilon }_0}}\right)E_{0t}\hfill \end{array}\\ 2E_{0i}=\left(1+\sqrt{\frac{\sqrt{1+{\alpha }^2}+1}{2}}+i\sqrt{\frac{\sqrt{1+{\alpha }^2}-1}{2}}\right)E_{0t},\\ \frac{E_{0t}}{E_{0i}}=\frac{2}{1+\sqrt{\frac{\sqrt{1+{\alpha }^2}+1}{2}}+i\sqrt{\frac{\sqrt{1+{\alpha }^2}-1}{2}}}\end{array}}$

Despejamos el cociente E_0r/E_0i

${\displaystyle \begin{array}{l}\begin{array}{l}\{\begin{array}{l}{E}_{0i}+E_{0r}=E_{0t}\\ \sqrt{\frac{{\epsilon }_0}{{\mu }_0}}\left(E_{0i}-E_{0r}\right)=\frac{k_2}{\omega {\mu }_0}{E}_{0t}\end{array}\hfill \\ \left(1-\sqrt{\frac{{\epsilon }_0}{{\mu }_0}}\frac{\omega {\mu }_0}{k_2}\right)E_{0i}+\left(1+\sqrt{\frac{{\epsilon }_0}{{\mu }_0}}\frac{\omega {\mu }_0}{k_2}\right)E_{0r}=0\hfill \end{array}\\ \frac{E_{0r}}{E_{0i}}=\frac{1-\sqrt{\frac{\sqrt{1+{\alpha }^2}+1}{2}}-i\sqrt{\frac{\sqrt{1+{\alpha }^2}-1}{2}}}{1+\sqrt{\frac{\sqrt{1+{\alpha }^2}+1}{2}}+i\sqrt{\frac{\sqrt{1+{\alpha }^2}-1}{2}}}\end{array}}$

Coeficientes de reflexión y transmisión.

Véase el apartado Ecuaciones de Fresnel, Coeficientes de reflexión y transmisión

El coeficiente de reflexión es

${\displaystyle \begin{array}{l}R=\frac{E_{0r}^2}{E_{0i}^2}\\ R=\frac{1-\sqrt{\frac{\sqrt{1+{\alpha }^2}+1}{2}}-i\sqrt{\frac{\sqrt{1+{\alpha }^2}-1}{2}}}{1+\sqrt{\frac{\sqrt{1+{\alpha }^2}+1}{2}}+i\sqrt{\frac{\sqrt{1+{\alpha }^2}-1}{2}}}·\frac{1-\sqrt{\frac{\sqrt{1+{\alpha }^2}+1}{2}}+i\sqrt{\frac{\sqrt{1+{\alpha }^2}-1}{2}}}{1+\sqrt{\frac{\sqrt{1+{\alpha }^2}+1}{2}}-i\sqrt{\frac{\sqrt{1+{\alpha }^2}-1}{2}}}\\ R=\frac{1+\sqrt{1+{\alpha }^2}-2\sqrt{\frac{\sqrt{1+{\alpha }^2}+1}{2}}}{1+\sqrt{1+{\alpha }^2}+2\sqrt{\frac{\sqrt{1+{\alpha }^2}+1}{2}}}\end{array}}$

El coeficiente de transmisión es

${\displaystyle \begin{array}{l}T=\frac{n_2}{n_1}\frac{E_{0t}^2}{E_{0i}^2}\\ n_2=\frac{c}{v_2}=k_2\frac{c}{\omega }=\frac{1}{\omega \sqrt{{\epsilon }_0{\mu }_0}}\omega \sqrt{\frac{{\epsilon }_0{\mu }_0}{2}\left(\sqrt{1+{\alpha }^2}+1\right)}=\sqrt{\frac{\sqrt{1+{\alpha }^2}+1}{2}}\\ T=\frac{n_2}{n_1}\frac{E_{0t}^2}{E_{0i}^2}=\frac{\sqrt{\frac{\sqrt{1+{\alpha }^2}+1}{2}}}{1}\frac{2}{1+\sqrt{\frac{\sqrt{1+{\alpha }^2}+1}{2}}+i\sqrt{\frac{\sqrt{1+{\alpha }^2}-1}{2}}}·\frac{2}{1+\sqrt{\frac{\sqrt{1+{\alpha }^2}+1}{2}}-i\sqrt{\frac{\sqrt{1+{\alpha }^2}-1}{2}}}=\\ =\frac{4\sqrt{\frac{\sqrt{1+{\alpha }^2}+1}{2}}}{1+\sqrt{1+{\alpha }^2}+2\sqrt{\frac{\sqrt{1+{\alpha }^2}+1}{2}}}\end{array}}$

v es la velocidad de propagación de las ondas electromagnéticas en un medio, c es la velocidad de propagación en el vacío.

Representamos los coeficientes R y T en función de α

R=@(x) (1+sqrt(1+x.^2)-2*sqrt((sqrt(1+x.^2)+1)/2)).
/(1+sqrt(1+x.^2)+2*sqrt((sqrt(1+x.^2)+1)/2));
T=@(x) 4*sqrt((sqrt(1+x.^2)+1)/2)./(1+sqrt(1+x.^2)+2*sqrt((sqrt(1+x.^2)+1)/2));
hold on
fplot(R,[0,300])
fplot(T,[0,300])
line([0,sqrt(288)],[0.5,0.5],'lineStyle','--')
line([sqrt(288),sqrt(288)],[0,0.5],'lineStyle','--')
hold off
grid on
xlabel('\alpha')
ylabel('R,T')
title('Coeficientes reflexión y transmisión')

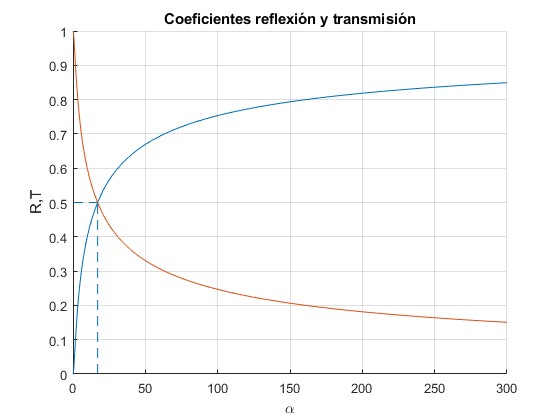
Para un buen conductor α es grande y el coeficiente de transmisión T tiende a cero, lo que explica el hecho de que los metales reflejen bien las ondas electromagnéticas

Los coeficientes coinciden R=T=0.5 para el valor α, señalado en la figura

${\displaystyle \begin{array}{l}1+\sqrt{1+{\alpha }^2}-2\sqrt{\frac{\sqrt{1+{\alpha }^2}+1}{2}}=4\sqrt{\frac{\sqrt{1+{\alpha }^2}+1}{2}}\\ 1+\sqrt{1+{\alpha }^2}=6\sqrt{\frac{\sqrt{1+{\alpha }^2}+1}{2}}\\ 1+1+{\alpha }^2+2\sqrt{1+{\alpha }^2}=36\frac{\sqrt{1+{\alpha }^2}+1}{2}\\ 16\sqrt{1+{\alpha }^2}={\alpha }^2-16\\ 256\left(1+{\alpha }^2\right)={\alpha }^4+256-32{\alpha }^2\\ {\alpha }^2\left({\alpha }^2-288\right)=0\\ \alpha =\sqrt{288}\end{array}}$

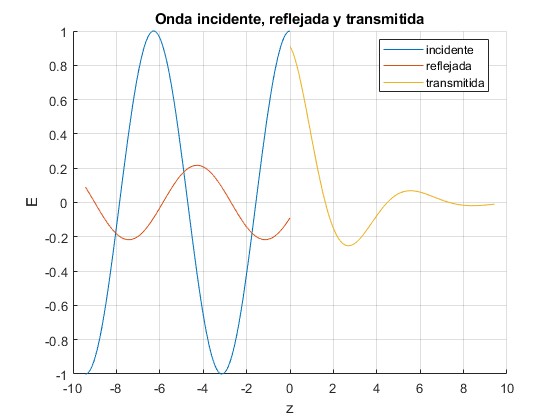
Onda incidente, reflejada y transmitida

${\displaystyle \begin{array}{l}{\overrightarrow{E}}_i=E_{0i}\exp \left(i\left(k_{1}z-\omega t\right)\right)\widehat{i}\\ {\overrightarrow{E}}_r=E_{0r}\exp \left(i\left(k_{1}z+\omega t\right)\right)\widehat{i}\\ {\overrightarrow{E}}_t=E_{0t}\exp \left(i\left(k_{2}z-\omega t\right)\right)\widehat{i}\end{array}}$

Los números de onda y las amplitudes de las ondas reflejada y transmitida son

${\displaystyle \begin{array}{l}{k}_1=\frac{\omega }{c}=\omega \sqrt{{\epsilon }_0{\mu }_0}\\ k_2=\left(\omega \sqrt{\frac{{\epsilon }_0{\mu }_0}{2}\left(\sqrt{1+{\alpha }^2}+1\right)}+i\omega \sqrt{\frac{{\epsilon }_0{\mu }_0}{2}\left(\sqrt{1+{\alpha }^2}-1\right)}\right)=k_1\left(\sqrt{\frac{\sqrt{1+{\alpha }^2}+1}{2}}+i\sqrt{\frac{\sqrt{1+{\alpha }^2}-1}{2}}\right)=a+ib\\ \frac{E_{0r}}{E_{0i}}=\frac{1-\sqrt{\frac{\sqrt{1+{\alpha }^2}+1}{2}}-i\sqrt{\frac{\sqrt{1+{\alpha }^2}-1}{2}}}{1+\sqrt{\frac{\sqrt{1+{\alpha }^2}+1}{2}}+i\sqrt{\frac{\sqrt{1+{\alpha }^2}-1}{2}}}=A+iB\\ \frac{E_{0t}}{E_{0i}}=\frac{2}{1+\sqrt{\frac{\sqrt{1+{\alpha }^2}+1}{2}}+i\sqrt{\frac{\sqrt{1+{\alpha }^2}-1}{2}}}=C+iD\end{array}}$

En el instante t=0

${\displaystyle \begin{array}{l}{E}_i=\mathrm{Re}\left(\exp \left(i{k}_{1}z\right)\right)=E_{0i}\cos \left(k_{1}z\right)\\ E_r=E_{0i}\mathrm{Re}\left(\left(A+iB\right)\exp \left(i{k}_{1}z\right)\right)=E_{0i}\left(A\cos \left(k_{1}z\right)-B\sin \left(k_{1}z\right)\right)\\ E_t=E_{0i}\mathrm{Re}\left(\left(C+iD\right)\exp \left(i{k}_{2}z\right)\right)=E_{0i}\mathrm{Re}\left(\left(C+iD\right)\exp \left(i\left(a+ib\right)z\right)\right)=E_{0i}\exp (-bz)\left(C\cos \left(az\right)-D\sin \left(az\right)\right)\end{array}}$

El símbolo Re significa la parte real del número complejo

Representamos la onda incidente, reflejada y transmitida para un mal conductor α=1. Tomamos k₁=1 y E_0i=1

alfa=1; 
re=(1-sqrt((sqrt(1+alfa^2)+1)/2)-1i*sqrt((sqrt(1+alfa^2)-1)/2))/
(1+sqrt((sqrt(1+alfa^2)+1)/2)+1i*sqrt((sqrt(1+alfa^2)-1)/2));
te=2/(1+sqrt((sqrt(1+alfa^2)+1)/2)+1i*sqrt((sqrt(1+alfa^2)-1)/2));
k2=sqrt((sqrt(1+alfa^2)+1)/2)+1i*sqrt((sqrt(1+alfa^2)-1)/2);
in=@(z) cos(z);
r=@(z) real(re)*cos(z)-imag(re)*sin(z);
t=@(z) exp(-imag(k2)*z).*(real(te)*cos(real(k2)*z)-imag(te)*sin(real(k2)*z));
hold on
fplot(@(z) cos(z),[-3*pi,0]) %incidente
fplot(r,[-3*pi,0]) %reflejada
fplot(t,[0,3*pi]) %transmitida
hold off
grid on
xlabel('z')
legend('incidente','reflejada','transmitida','location','best')
ylabel('E')
title('Onda incidente, reflejada y transmitida')

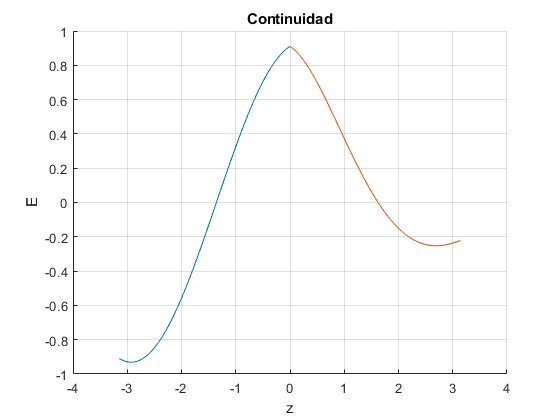
Comprobamos la continuidad de las ondas electromagnéticas en la superficie de separación z=0, en el primer medio tenemos la superposición E_i+E_r, en el segundo medio, solamente la onda transmitida E_t

alfa=1;
re=(1-sqrt((sqrt(1+alfa^2)+1)/2)-1i*sqrt((sqrt(1+alfa^2)-1)/2))/
(1+sqrt((sqrt(1+alfa^2)+1)/2)+1i*sqrt((sqrt(1+alfa^2)-1)/2));
te=2/(1+sqrt((sqrt(1+alfa^2)+1)/2)+1i*sqrt((sqrt(1+alfa^2)-1)/2));
k2=sqrt((sqrt(1+alfa^2)+1)/2)+1i*sqrt((sqrt(1+alfa^2)-1)/2);
in=@(z) cos(z);
r=@(z) real(re)*cos(z)-imag(re)*sin(z);
t=@(z) exp(-imag(k2)*z).*(real(te)*cos(real(k2)*z)-imag(te)*sin(real(k2)*z));
hold on
me=@(z) in(z)+r(z);
fplot(me,[-pi,0]) %medio 1
fplot(t,[0,pi]) %medio 2
hold off
grid on
xlabel('z')
ylabel('E')
title('Continuidad')

Representamos la onda incidente, reflejada y transmitida para un buen conductor α=10

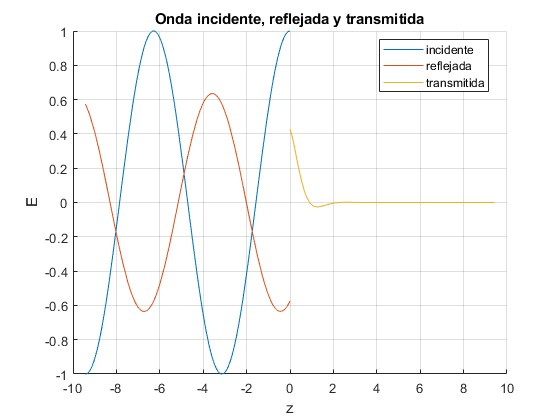
La onda transmitida se amortigua fuertemente cuando penetra en el segundo medio conductor

Referencias

Paul Lorrain, Dale R. Corson. Campos y ondas electromagnéticas. Selecciones Científicas. 1972

J. Pierrus. Solved Problems in Classical Electromagnetism. Analytical and numerical solutions with comments. Oxford University Press (2018). Question 10.13, pp. 482-486.