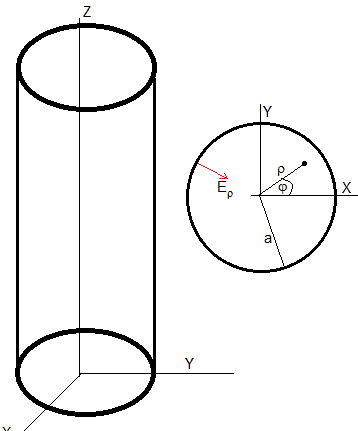
Ondas guiadas. Guía de onda circular
En esta página, estudiaremos
el modo TE, ondas transversales eléctricas
el modo TM, ondas transversales magnéticas
en una guía circular
Supongamos que el medio en el que se propaga la onda electromagnética es isótropo, lineal y homogéneo, no conductor. La onda electromagnética se propaga a lo largo del eje Z. En coordenadas cilíndricas
E
→
=
E
ρ
ρ
^
+
E
φ
φ
^
+
E
z
k
^
, {
E
ρ
=
E
0 ρ
exp (
i (
k z − ω t
)
)
E
φ
=
E
0 φ
exp (
i (
k z − ω t
)
)
E
z
=
E
0 z
exp (
i (
k z − ω t
)
)
B
→
=
B
ρ
ρ
^
+
B
φ
φ
^
+
B
z
k
^
, {
B
ρ
=
B
0 ρ
exp (
i (
k z − ω t
)
)
B
φ
=
B
0 φ
exp (
i (
k z − ω t
)
)
B
z
=
B
0 z
exp (
i (
k z − ω t
)
)
Las amplitudes E0ρ , E0φ , E0z , B0ρ , B0φ , B0z son funciones de ρ e φ , que por ahora no conocemos, la dependencia con z y t aparece en la función exponencial. La onda electromagnética no es transversal ya que tiene una compoenete Ez a lo largo de la dirección de propagación
Apicamos la ley de Faraday en forma diferencial
∇
→
×
E
→
= −
∂
B
→
∂ t
(
1
ρ
∂
E
z
∂ φ
−
∂
E
φ
∂ z
)
ρ
^
+ (
∂
E
ρ
∂ z
−
∂
E
z
∂ ρ
)
φ
^
+
1
ρ
(
∂
∂ ρ
(
ρ
E
φ
) −
∂
E
ρ
∂ φ
)
k
^
= −
∂
∂ t
(
B
ρ
ρ
^
+
B
φ
φ
^
+
B
z
k
^
)
{
1
ρ
∂
E
0 z
∂ φ
e
i ( k z − ω t )
− i k
E
0 φ
e
i ( k z − ω t )
= i ω
B
0 ρ
e
i ( k z − ω t )
i k
E
0 ρ
e
i ( k z − ω t )
−
∂
E
0 z
∂ ρ
e
i ( k z − ω t )
= i ω
B
0 φ
e
i ( k z − ω t )
1
ρ
(
∂ (
ρ
E
0 φ
)
∂ ρ
e
i ( k z − ω t )
−
∂
E
0 ρ
∂ φ
e
i ( k z − ω t )
) = i ω
B
0 z
e
i ( k z − ω t )
{
1
ρ
∂
E
0 z
∂ φ
− i k
E
0 φ
= i ω
B
0 ρ
i k
E
0 ρ
−
∂
E
0 z
∂ ρ
= i ω
B
0 φ
1
ρ
(
∂ (
ρ
E
0 φ
)
∂ ρ
−
∂
E
0 ρ
∂ φ
) = i ω
B
0 z
La ley de Ampère-Maxwell , sin corrientes
∇
→
×
B
→
−
1
c
2
∂
E
→
∂ t
= 0
(
1
ρ
∂
B
z
∂ φ
−
∂
B
φ
∂ z
)
ρ
^
+ (
∂
B
ρ
∂ z
−
∂
B
z
∂ ρ
)
φ
^
+
1
ρ
(
∂
∂ ρ
(
ρ
B
φ
) −
∂
B
ρ
∂ φ
)
k
^
−
1
c
2
∂
∂ t
(
E
ρ
ρ
^
+
E
φ
φ
^
+
E
z
k
^
) = 0
{
1
ρ
∂
B
0 z
∂ φ
− i k
B
0 φ
+
1
c
2
i ω
E
0 ρ
= 0
i k
B
0 ρ
−
∂
B
0 z
∂ ρ
+
1
c
2
i ω
E
0 φ
= 0
1
ρ
(
∂
∂ x
(
ρ
B
0 φ
) −
∂
B
0 ρ
∂ φ
) +
1
c
2
i ω
E
0 z
= 0
Las cuatro componentes transversales E0ρ , E0φ , B0ρ , B0φ se pueden deducir de las componentes longitudinales, E0z , B0z del siguiente modo
A partir de las ecuaciones
{
1
ρ
∂
B
0 z
∂ φ
− i k
B
0 φ
+
1
c
2
i ω
E
0 ρ
= 0
i k
E
0 ρ
−
∂
E
0 z
∂ ρ
= i ω
B
0 φ
Despejamos E0ρ y B0φ
E
0 ρ
=
i
γ
2
(
ω
ρ
∂
B
0 z
∂ φ
+ k
∂
E
0 z
∂ ρ
) ,
γ
2
=
ω
2
c
2
−
k
2
B
0 φ
=
i
γ
2
(
k
ρ
∂
B
0 z
∂ φ
+
ω
c
2
∂
E
0 z
∂ ρ
)
A partir de las ecuaciones
{
1
ρ
∂
E
0 z
∂ φ
− i k
E
0 φ
= i ω
B
0 ρ
i k
B
0 ρ
−
∂
B
0 z
∂ ρ
+
1
c
2
i ω
E
0 φ
= 0
Despejamos B0ρ y E0φ
E
0 φ
=
i
γ
2
(
k
ρ
∂
E
0 z
∂ φ
− ω
∂
B
0 z
∂ ρ
)
B
0 ρ
=
i
γ
2
(
k
∂
B
0 z
∂ ρ
−
ω
c
2
1
ρ
∂
E
0 z
∂ φ
)
Las ecuaciones de propagación de las ondas electromagnéticas son
{
∇
2
E
→
−
ε
0
μ
0
∂
2
E
→
∂
t
2
= 0
∇
2
B
→
−
ε
0
μ
0
∂
2
B
→
∂
t
2
= 0
La onda electromagnética se propaga a lo largo del eje Z
(
1
ρ
∂
∂ ρ
(
ρ
∂
E
0 z
∂ ρ
) +
1
ρ
2
∂
2
E
0 z
∂
φ
2
)
e
i (
k z − ω t
)
−
k
2
E
0 z
e
i (
k z − ω t
)
+
ω
2
c
2
E
0 z
e
i (
k z − ω t
)
= 0
1
ρ
∂
∂ ρ
(
ρ
∂
E
0 z
∂ ρ
) +
1
ρ
2
∂
2
E
0 z
∂
φ
2
+ (
ω
2
c
2
−
k
2
)
E
0 z
= 0
1
ρ
∂
∂ ρ
(
ρ
∂
E
0 z
∂ ρ
) +
1
ρ
2
∂
2
E
0 z
∂
φ
2
+
γ
2
E
0 z
= 0
De modo similar
1
ρ
∂
∂ ρ
(
ρ
∂
B
0 z
∂ ρ
) +
1
ρ
2
∂
2
B
0 z
∂
φ
2
+
γ
2
B
0 z
= 0
Los valores del número de onda k son discretos y vienen determinados por la frecuencia ω de la onda electromagnética y por la geometría y características del medio en el que se propaga ε , μ (no conductor)
Resolvemos la ecuación diferencial utilizando el procedimiento de variables separadas
B
z
(
x , y , t
) = R ( ρ ) Ψ ( φ ) exp (
i (
k z − ω t
)
)
Introducimos en la ecuación diferencial
Ψ
1
ρ
∂
∂ ρ
(
ρ
∂ R
∂ ρ
) + R
1
ρ
2
∂
2
Ψ
∂
φ
2
+
γ
2
R Ψ = 0
ρ
R
∂
∂ ρ
(
ρ
∂ R
∂ ρ
) +
1
Ψ
∂
2
Ψ
∂
φ
2
+
γ
2
ρ
2
= 0
El segundo solamente función de φ . Convertimos una ecuación diferencial en un sistema de dos ecuaciones diferenciales cuya solución es sencilla
{
1
Ψ
d
2
Ψ
d
φ
2
= −
m
2
ρ
d
d ρ
(
ρ
d R
d ρ
) + (
γ
2
ρ
2
−
m
2
) R = 0
La solución de la primera ecuación diferencial es
Ψ (
φ
) = {
C
1
sin (
m φ
) +
C
2
cos (
m φ
) , m ≠ 0
C
1
+
C
2
φ , m = 0
Como la solución es periódica
Ψ (
φ
) = Ψ (
2 π + φ
)
C
1
sin (
m φ
) +
C
2
cos (
m φ
) =
C
1
sin (
m φ + 2 π m
) +
C
2
cos (
m φ + 2 π m
) =
C
1
sin (
m φ
) +
C
2
cos (
m φ
) =
C
1
{
sin (
m φ
) cos (
2 π m
) + cos (
m φ
) sin (
2 π m
) } +
C
2
{
cos (
m φ
) cos (
2 π m
) − sin (
m φ
) sin (
2 π m
) }
Esta igualdad es posible si m es entero
Resolvemos la segunda ecuación difeencial
ρ
2
d
2
R
d
ρ
2
+ ρ
d R
d ρ
+ (
γ
2
ρ
2
−
m
2
) R = 0
Sustituyendo r=ργ
r
2
d
2
R
d
r
2
+ r
d R
d r
+ (
r
2
−
m
2
) R = 0
La solución se expresa en términos de las funciones de Bessel
R ( r ) = A
J
m
( r ) + B
Y
m
( r )
R ( ρ ) = A
J
m
(
γ ρ
) + B
Y
m
(
γ ρ
)
Se descarta el segundo término ya que tiende a infinito cuando ρ →0
La expresión de la amplitud B0z del campo magnético es
B
0 z
= {
A
J
m
(
γ ρ
) (
C
1
sin (
m φ
) +
C
2
cos (
m φ
)
) , m ≠ 0
A
J
m
(
γ ρ
) (
C
1
+
C
2
φ
) , m = 0
Eligiendo un origen apropiado de ángulos podemos hacer que C 1 =0. Denominamos B 0 al producto A·C 2
Estudiamos el caso m ≠0
B
0 z
=
B
0
J
m
(
γ ρ
) cos (
m φ
)
La componente Bz
B
z
= Re {
B
0 z
exp (
i (
k z − ω t
)
) } =
B
0
J
m
(
γ ρ
) cos (
m φ
) cos (
k z − ω t
)
Derivamos B0z respecto de ρ e φ
∂
B
0 z
∂ ρ
=
B
0
d
J
m
(
γ ρ
)
d ρ
cos (
m φ
)
∂
B
0 z
∂ φ
= − m
B
0
J
m
(
γ ρ
) sin (
m φ
)
TE, ondas transversales eléctricas
Las ondas transversales eléctricas están caracterizadas por que Ez =0
Sea una guía circular de radio a que se extiende a lo largo del eje Z
La condición de contorno es
∂
B
z
∂ n
|
pared
= 0
, donde el símbolo n indica derivada en la dirección normal a la superficie metálica evaluada en la posición de dicha superficie de la guía. Esta condición es equivalente a la siguiente
Sabiendo que E0z =0, de la relación
E
0 φ
=
i
γ
2
(
k
ρ
∂
E
0 z
∂ φ
− ω
∂
B
0 z
∂ ρ
) = −
i
γ
2
ω
∂
B
0 z
∂ ρ
E
0 φ
|
ρ = a
=
−
i
γ
2
ω
∂
B
0 z
∂ ρ
|
ρ = a
= 0
El campo eléctrico es perpendicular a la superficie cilíndrica conductora
La condición de contorno en ρ=a
∂
B
z
∂ ρ
|
ρ = a
= 0
d
J
m
(
γ ρ
)
d ρ
|
ρ = a
= 0
La derivada de las funciones Jm (x ) de Bessel es
d
J
m
( x )
d k
=
m
x
J
m
( x ) −
J
m + 1
( x )
d
J
m
(
γ ρ
)
d ρ
=
m
ρ
J
m
(
γ ρ
) − γ
J
m + 1
(
γ ρ
)
Denominamos tm,n a las raíces de la la ecuación transcendente
m
a
J
m
(
γ a
) − γ
J
m + 1
(
γ a
) = 0
γ
m , n
=
t
m , n
a
ω
2
=
c
2
(
t
m , n
2
a
2
+
k
2
)
Para m =0, calculamos las raíces de la ecuación J 1 (x )=0
function guia_1
x=linspace(0,10,10);
f=@(x) besselj(1,x);
rr=raices(f,x);
disp('dJ_0(x)/dx=0')
disp( rr)
f=@(x) besselj(1,x)./x-besselj(2,x);
rr=raices(f,x);
disp('dJ_1(x)/dx=0')
disp (rr)
f=@(x) 2*besselj(2,x)./x-besselj(3,x);
rr=raices(f,x);
disp('dJ_2(x)/dx=0')
disp(rr)
function r = raices(f, x)
y=f(x);
indices=find(y(1:end-1).*y(2:end)<0);
r=zeros(1,length(indices));
for k=1:length(indices)
r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
end
end
end
dJ_0(x)/dx=0, 3.8317 7.0156
dJ_1(x)/dx=0, 1.8412 5.3314 8.5363
dJ_2(x)/dx=0, 3.0542 6.7061 9.9695
Amplitudes
Conocido B0z y E0z =0, determinamos las otras amplitudes de las componentes del campo eléctrico y magnético
Componente Eρ
E
0 ρ
=
i
γ
2
(
ω
ρ
∂
B
0 z
∂ φ
+ k
∂
E
0 z
∂ ρ
) =
i
γ
2
ω
ρ
∂
B
0 z
∂ φ
E
0 ρ
= −
i
γ
2
ω
ρ
m
B
0
J
m
(
γ ρ
) sin (
m φ
)
E
ρ
= Re {
E
0 ρ
exp (
i (
k z − ω t
)
) } =
ω
B
0
γ
2
m
ρ
J
m
(
γ ρ
) sin (
m φ
) sin (
k z − ω t
)
Componente Eφ
E
0 φ
=
i
γ
2
(
k
ρ
∂
E
0 z
∂ φ
− ω
∂
B
0 z
∂ ρ
) = −
i
γ
2
ω
∂
B
0 z
∂ ρ
E
0 φ
= −
i
γ
2
ω
B
0
d
J
m
(
γ ρ
)
d ρ
cos (
m φ
)
E
φ
= Re {
E
0 φ
exp (
i (
k z − ω t
)
) } =
ω
B
0
γ
2
d
J
m
(
γ ρ
)
d ρ
cos (
m φ
) sin (
k z − ω t
)
Componente Bρ
B
0 ρ
=
i
γ
2
(
k
∂
B
0 z
∂ ρ
−
ω
c
2
1
ρ
∂
E
0 z
∂ φ
) =
i
γ
2
k
∂
B
0 z
∂ ρ
B
0 ρ
=
i
γ
2
k
B
0
d
J
m
(
γ ρ
)
d ρ
cos (
m φ
)
B
ρ
= Re {
B
0 ρ
exp (
i (
k z − ω t
)
) } = −
k
B
0
γ
2
d
J
m
(
γ ρ
)
d ρ
cos (
m φ
) sin (
k z − ω t
)
Componente Bφ
B
0 φ
=
i
γ
2
(
k
ρ
∂
B
0 z
∂ φ
+
ω
c
2
∂
E
0 z
∂ ρ
) =
i
γ
2
k
ρ
∂
B
0 z
∂ φ
B
0 φ
= −
i
γ
2
k
ρ
m
B
0
J
m
(
γ ρ
) sin (
m φ
)
B
φ
= Re {
B
0 φ
exp (
i (
k z − ω t
)
) } =
k
B
0
γ
2
m
ρ
J
m
(
γ ρ
) sin (
m φ
) sin (
k z − ω t
)
Resumiendo, las componentes del campo eléctrico
E
→
y del campo magbético
B
→
, son
E
→
= {
E
ρ
=
ω
B
0
γ
2
m
ρ
J
m
(
γ ρ
) sin (
m φ
) sin (
k z − ω t
)
E
φ
=
ω
B
0
γ
2
d
J
m
(
γ ρ
)
d ρ
cos (
m φ
) sin (
k z − ω t
)
E
z
= 0
B
→
= {
B
ρ
= −
k
B
0
γ
2
d
J
m
(
γ ρ
)
d ρ
cos (
m φ
) sin (
k z − ω t
)
B
φ
=
k
B
0
γ
2
m
ρ
J
m
(
γ ρ
) sin (
m φ
) sin (
k z − ω t
)
B
z
=
B
0
J
m
(
γ ρ
) cos (
m φ
) cos (
k z − ω t
)
TM, ondas transversales magnéticas
Las ondas transversales magnéticas están caracterizadas por que Bz =0.
La solución de la ecuación diferencial
1
ρ
∂
∂ ρ
(
ρ
∂
E
0 z
∂ ρ
) +
1
ρ
2
∂
2
E
0 z
∂
φ
2
+
γ
2
E
0 z
= 0
es, de modo análogo al primer apartado
E
0 z
(
ρ , φ , t
) = {
A
J
m
(
γ ρ
) (
C
1
sin (
m φ
) +
C
2
cos (
m φ
)
) , m ≠ 0
A
J
m
(
γ ρ
) (
C
1
+
C
2
φ
) , m = 0
Eligiendo un origen apropiado de ángulos podemos hacer que C 1 =0. Denominamos E 0 al producto A·C 2
E
0 z
=
E
0
J
m
(
γ ρ
) cos (
m φ
)
La condición de contorno Ez (a )=0 para ρ=a implica
J
m
(
γ a
) = 0
γ
m , n
=
s
m , n
a
ω
2
=
c
2
(
s
m , n
2
a
2
+
k
2
)
sm,n son las raíces de la ecuación transcendente
function guia
x=linspace(0,10,10);
f=@(x) besselj(0,x);
rr=raices(f,x);
disp('J_0(x)=0')
disp( rr)
f=@(x) besselj(1,x);
rr=raices(f,x);
disp('J_1(x)=0')
disp (rr)
f=@(x) besselj(2,x);
rr=raices(f,x);
disp('J_2(x)=0')
disp(rr)
function r = raices(f, x)
y=f(x);
indices=find(y(1:end-1).*y(2:end)<0);
r=zeros(1,length(indices));
for k=1:length(indices)
r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
end
end
end
J_0(x)=0, 2.4048 5.5201 8.6537
J_1(x)=0, 3.8317 7.0156
J_2(x)=0, 5.1356 8.4172
Amplitudes
La componente E0z es
E
0 z
=
E
0
J
m
(
γ ρ
) cos (
m φ
)
E
z
= Re {
E
0 z
exp (
i (
k z − ω t
)
) } =
E
0
J
m
(
γ ρ
) cos (
m φ
) cos (
k z − ω t
)
Conocido E0z y B0z =0, determinamos las otras amplitudes de las componentes del campo eléctrico y magnético
Componente Eρ
E
0 ρ
=
i
γ
2
(
ω
ρ
∂
B
0 z
∂ φ
+ k
∂
E
0 z
∂ ρ
) =
i
γ
2
k
∂
E
0 z
∂ ρ
E
0 ρ
=
i
γ
2
k
E
0
d
J
m
(
γ ρ
)
d ρ
cos (
m φ
)
E
ρ
= Re {
E
0 ρ
exp (
i (
k z − ω t
)
) } = −
k
E
0
γ
2
d
J
m
(
γ ρ
)
d ρ
cos (
m φ
) sin (
k z − ω t
)
Componente Eφ
E
0 φ
=
i
γ
2
(
k
ρ
∂
E
0 z
∂ φ
− ω
∂
B
0 z
∂ ρ
) =
i
γ
2
k
ρ
∂
E
0 z
∂ φ
E
0 φ
= −
i
γ
2
k
ρ
E
0
J
m
(
γ ρ
) m sin (
m φ
)
E
φ
= Re {
E
0 φ
exp (
i (
k z − ω t
)
) } =
k
E
0
γ
2
m
ρ
J
m
(
γ ρ
) sin (
m φ
) sin (
k z − ω t
)
Para ρ=a , Jm (γa )=0, por lo que Eφ =0, el campo eléctrico tiene dirección radial perpendicular a la superficie cilíndrica conductora
Componente Bρ
B
0 ρ
=
i
γ
2
(
k
∂
B
0 z
∂ ρ
−
ω
c
2
1
ρ
∂
E
0 z
∂ φ
) = −
i
γ
2
ω
c
2
1
ρ
∂
E
0 z
∂ φ
B
0 ρ
=
i
γ
2
ω
c
2
1
ρ
E
0
m
J
m
(
γ ρ
) sin (
m φ
)
B
ρ
= Re {
B
0 ρ
exp (
i (
k z − ω t
)
) } = −
ω
E
0
c
2
γ
2
m
ρ
J
m
(
γ ρ
) sin (
m φ
) sin (
k z − ω t
)
Componente Bφ
B
0 φ
=
i
γ
2
(
k
ρ
∂
B
0 z
∂ φ
+
ω
c
2
∂
E
0 z
∂ ρ
) =
i
γ
2
ω
c
2
∂
E
0 z
∂ ρ
B
0 φ
=
i
γ
2
ω
c
2
E
0
d
J
m
(
γ ρ
)
d ρ
cos (
m φ
)
B
φ
= Re {
B
0 φ
exp (
i (
k z − ω t
)
) } = −
ω
E
0
c
2
γ
2
d
J
m
(
γ ρ
)
d ρ
cos (
m φ
) sin (
k z − ω t
)
Resumiendo, las componentes del campo eléctrico
E
→
y del campo magnético
B
→
, son
E
→
= {
E
ρ
= −
k
E
0
γ
2
d
J
m
(
γ ρ
)
d ρ
cos (
m φ
) sin (
k z − ω t
)
E
φ
=
k
E
0
γ
2
m
ρ
J
m
(
γ ρ
) sin (
m φ
) sin (
k z − ω t
)
E
z
=
E
0
J
m
(
γ ρ
) cos (
m φ
) cos (
k z − ω t
)
B
→
= {
B
ρ
= −
ω
E
0
c
2
γ
2
m
ρ
J
m
(
γ ρ
) sin (
m φ
) sin (
k z − ω t
)
B
φ
= −
ω
E
0
c
2
γ
2
d
J
m
(
γ ρ
)
d ρ
cos (
m φ
) sin (
k z − ω t
)
B
z
= 0
Nota: las expresiones de Bρ y Bφ difieren de las proporcionadas en la referencia, véase la página 372
Referencias
J. Pierrus. Solved Problems in Classical Electromagnetism. Analytical and numerical solutions with comments. Oxford University Press (2018). Question 7.16, pp. 369-372