Reflexión y transmisión de ondas.
La ecuación del movimiento ondulatorio armónico de frecuencia angular ω es
v es la velocidad de propagación, k=2π/λ es el número de onda, A0 es la amplitud y φ la fase inicial
Es conveniente expresar la ecuación del movimiento ondulatorio armónico en forma compleja
La amplitud compleja A=A0exp(iφ), contiene la información de la amplitud y fase. El desplazamiento vertical de la cuerda en la posición x y en el instante t, es la parte real y(x,t)=ReΨ(x,t)
Dos cuerdas unidas en el origen
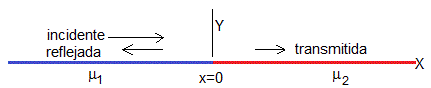
Supongamos que un movimiento ondulatorio se propaga a lo largo de dos cuerdas, la cuerda de la izquierda tiene una densidad lineal μ1 y la cuerda de la derecha tiene una densidad lineal μ2.
El movimiento ondulatorio transversal se propaga en ellas con velocidades, respectivamente, de
Siendo T la tensión de las cuerdas.
El movimiento ondulatorio incidente, se propaga de izquierda a derecha, en la región x<0, con A=A0exp(iφa)
El movimiento ondulatorio reflejado, se propaga de derecha a izquierda, en la región x<0, con B=B0exp(iφb)
El movimiento ondulatorio transmitido, se propaga de izquierda a derecha, en la región x>0, con C=C0exp(iφc)
En la región
x<0, tenemos la superposición de dos movimientos ondulatorios, inicidente y reflejado
x>0, tenemos el movimiento ondulatorio transmitido
Condiciones en x=0
La cuerda es continua
Fuerza vertical Fy en cualquier punto de la cuerda.
Por tanto en x=0, se tiene que cumplir
k1(A-B)=k2C
Desde el punto de vista matemático decimos, que en el punto de discontinuidad situado en el origen, la función que describe el movimiento ondulatorio debe ser continua y también lo debe ser su derivada primera.
Tenemos dos ecuaciones, que nos permiten relacionar la amplitud de la onda reflejada B y transmitida C en términos de la amplitud de la onda incidente A
Expresando el número de onda k1 y k2 en términos de las velocidades de propagación respectivas v1 y v2
Si v1 es menor que v2, las ondas incidente y reflejada están en fase, en caso contrario en opocición de fase
Actividades
Se representan dos cuerdas unidas en el origen. En la primera región de color blanco, tenemos la superposición Ψ1 del movimiento ondulatorio incidente y reflejado dibujados en una línea de color azul. En la segunda región de color rosa, tenemos el movimiento ondulatorio transmitido Ψ2 dibujado por una línea de color azul. En el origen, la función que describe el movimiento ondulatorio es continua y también su derivada primera.
Asimismo, se representa en la región de la izquierda, el movimiento ondulatorio incidente y reflejado, en los colores que se indican en la parte inferior.
Observamos que la onda transmitida siempre está en fase con la onda incidente. Sin embargo, la onda reflejada puede estar en fase o en oposición de fase dependiendo de que la velocidad de propagación en el segundo medio v2 sea mayor que en el primero v1 o al contrario.
Se introduce
- La frecuencia del movimiento ondulatorio, en el control titulado Frecuencia. Esta magnitud no cambia al propagarse un mismo movimiento ondulatorio por distintas medios.
- La velocidad de propagación de las ondas en el medio1 (a la izquierda), en el control titulado Velocidad medio1
- La velocidad de propagación de las ondas en el medio2 (a la derecha), en el control titulado Velocidad medio2
Se pulsa el botón titulado Nuevo
Tres cuerdas unidas
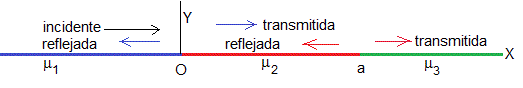
Supongamos que un movimiento ondulatorio se propaga a lo largo de tres cuerdas, la cuerda de la izquierda (-∞<x<0) tiene una densidad lineal μ1, la cuerda central, un segmento de longitud a, μ2 y la de la derecha (x>a), μ3.
El movimiento ondulatorio transversal se propaga en ellas con velocidades, respectivamente, de
En la región, x<0, tenemos un movimiento ondulatorio incidente y otro reflejado en x=0, que se propagan con velocidad v1
En la región, 0<x<a, tenemos un movimiento ondulatorio transmitido y otro reflejado en x=a, que se propagan con velocidad v2
En la región, x>a, tenemos un movimiento ondulatario transmitido, que se propaga con velocidad v3
Condiciones en el x=0 y en x=a
La cuerda es continua en x=0
Fuerza vertical Fy en x=0, tiene que cumplir
La cuerda es continua en x=a
Fuerza vertical Fy en x=a, tiene que cumplir
Despejamos los coeficientes complejos B, C, D y E en función de A en el sistema de cuatro ecuaciones
En las dos primeras ecuaciones eliminamos B.
En las dos últimas ecuaciones despejamos, C y D
Expresamos el coeficiente E en términos de A
En las dos primeras ecuaciones, despejamos B
Casos particulares
Las cuerdas de los extremos tienen la misma densidad, μ1=μ3, por lo que k1=k3
El coeficiente B=0, cuando k2a=nπ, n=1,2,3...
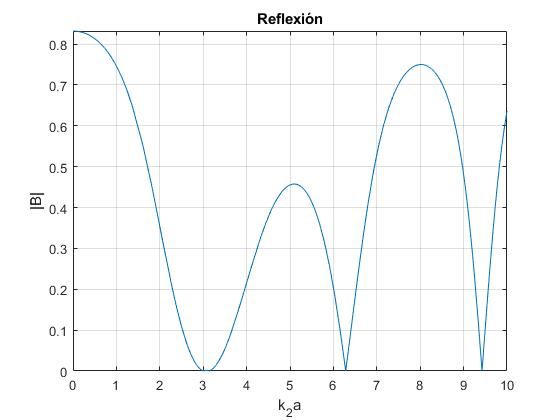
Fijamos la densidad de las cuerdas extremas de modo que k1=k3=3, la longitud a=1 del segmento de cuerda intermedia. Vamos cambiando la densidad de ésta o bien, k2. Observamos que el módulo de |B| se hace cero para ciertos valores de k2a
k1=3;
a=1;
r=@(k2) abs(1i*(k1^2-k2.^2).*sin(k2*a)./(k1*k2.*(2*cos(k2*a)-
1i*(k1^2+k2.^2).*sin(k2*a)./(k1*k2))));
fplot(r,[0,10])
grid on
xlabel('k_2a')
ylabel('|B|')
title('Reflexión')
Las cuerdas tienen una densidad tal que
El coeficiente B=0, cuando k2a=(2n+1)π/2, n=0,1,2,3...
Sistema multicapa
En general, podemos imaginar un sistema formado por capas de espesor a, cuyas velocidades de propagación sean alternativamente, v1 y v2, o los números de onda k1=ω/v1 y k2=ω/v2, ω es la frecuencia angular.
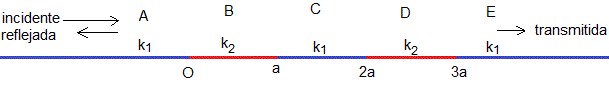
Como hemos apreciado, el cálculo de las amplitudes del movimiento ondulatorio reflejado B y transmitido E se vuelven cada vez más complicados. La alternativa es la de operar con matrices complejas de dimensión 2×2, de modo similar a las barreras de potencial.
Consideremos el ejemplo de la figura. El vector A contiene la información de la amplitud del movimiento ondulatorio incidente
La continuidad de la función que describe el movimiento ondulatorio en los distintos intervalos y de su derivada en los puntos x=0, x=a, x=2a, x=3a, dan lugar a un sistema de ecuaciones que en forma matricial se expresa
Asignamos a E1=1 y calculamos el vector D, para ello precisamos la matriz inversa que multiplica a dicho vector D. Por ejemplo, si AX=BY, X=A-1BY
El producto de una matriz por su inversa es la matriz unidad
>> syms q x; >> A=[x,1/x;q*x,-q/x]; >> inv(A) ans = [ 1/(2*x), 1/(2*q*x)] [ x/2, -x/(2*q)]
Una vez calculado el vector D, calculamos el C, luego el B y por último el A.
Para que la amplitud del movimiento ondulatorio incidente sea la unidad y su fase φa=0, dividimos los vectores por
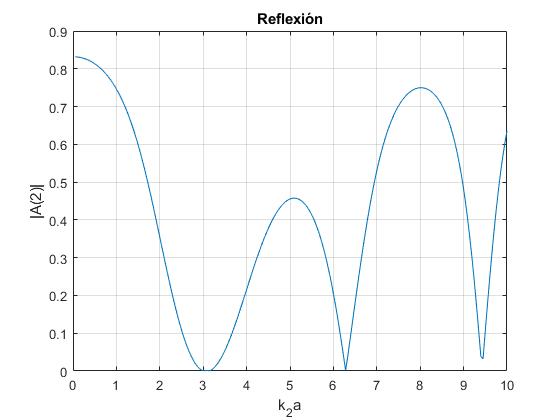
Volvemos sobre el ejemplo estudiado en el primer caso particular, una sola capa de anchura a=1 cuya velocidad de propagación es v2, el número de onda k2. Supondremos que k1=3. Representamos la amplitud del movimiento ondulatorio reflejado
%matriz
f=@(z,q) [exp(1i*q*z), exp(-1i*q*z); q*exp(1i*q*z), -q*exp(-1i*q*z)];
%inversa
g=@(z,q) [exp(-1i*q*z), exp(-1i*q*z)/q; exp(1i*q*z), -exp(1i*q*z)/q]/2;
k1=3;
kk2=linspace(0,10,200);
z=zeros(1,length(kk2));
a=1;
j=1;
for k2=kk2
B=g(a,k2)*f(a,k1)*[1;0];
A=g(0,k1)*f(0,k2)*B;
A=A/A(1);
z(j)=abs(A(2));
j=j+1;
end
plot(kk2,z)
grid on
xlabel('k_2a')
ylabel('|A(2)|')
title('Reflexión')
Representamos el movimiento ondulatorio (en color negro), en los tres intervalos. En el primer intervalo (-∞<x<0) en color rojo, se representa la onda incidente, en azul, la reflejada y en negro, la superposición. En el segundo intervalo (0<x<a) en color rojo, se representa la onda transmitida, en azul, la reflejada y en negro, la superposición. En el tercer intervalo (x>a) en negro, el movimiento ondulatorio transmitido
f=@(z,q) [exp(1i*q*z), exp(-1i*q*z); q*exp(1i*q*z), -q*exp(-1i*q*z)]; %matriz
g=@(z,q) [exp(-1i*q*z), exp(-1i*q*z)/q; exp(1i*q*z), -exp(1i*q*z)/q]/2; %inversa
k1=3;
k2=1;
a=1;
B=g(a,k2)*f(a,k1)*[1;0];
A=g(0,k1)*f(0,k2)*B;
C=1/A(1);
B=B/A(1);
A=A/A(1);
hold on
%cuerda -inf<x<0
fplot(@(x) real(A(1)*exp(1i*k1*x)+A(2)*exp(-1i*k1*x)),[-3,0],'k')
fplot(@(x) real(A(1)*exp(1i*k1*x)),[-3,0],'r') %incidente
fplot(@(x) real(A(2)*exp(-1i*k1*x)),[-3,0],'b') %reflejada
%cuerda 0<x<a
fplot(@(x) real(B(1)*exp(1i*k2*x)+B(2)*exp(-1i*k2*x)),[0,a],'k')
fplot(@(x) real(B(1)*exp(1i*k2*x)),[0,a],'r') %transmitida
fplot(@(x) real(B(2)*exp(-1i*k2*x)),[0,a],'b') %reflejada
%cuerda x>a
fplot(@(x) real(C*exp(1i*k1*x)),[a,4],'k') %transmitida
hold off
grid on
xlabel('x')
ylabel('y')
title('Movimiento ondulatorio')
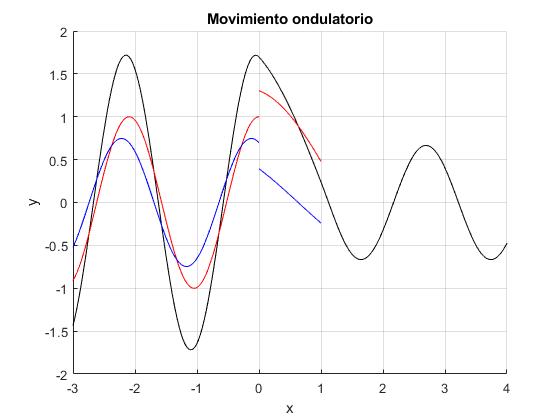
Si cambiamos el valor de k2 por un multiplo entero de π veremos que desaparece el movimiento ondulatario reflejado
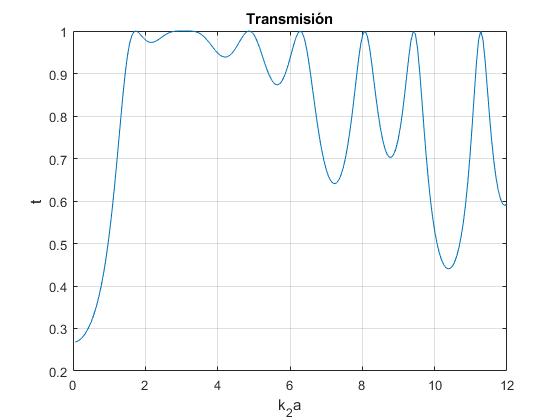
Consideremos un sistema multicapa, con N=3, representado al principio de este apartado. Representamos el módulo de la amplitud del movimiento ondulatorio transmitido
a=1;
k1=3;
f=@(z,q) [exp(1i*q*z), exp(-1i*q*z); q*exp(1i*q*z), -q*exp(-1i*q*z)];
g=@(z,q) [exp(-1i*q*z), exp(-1i*q*z)/q; exp(1i*q*z), -exp(1i*q*z)/q]/2;
kk2=linspace(0,12,200);
z=zeros(1,length(kk2));
j=1;
N=3;
for k2=kk2
A=[1;0];
for n=N:-2:0
A=g(n*a,k2)*f(n*a,k1)*A;
A=g((n-1)*a,k1)*f((n-1)*a,k2)*A;
end
z(j)=abs(1/A(1)); %transmisión
j=j+1;
end
plot(kk2,z)
grid on
xlabel('k_2a')
ylabel('t')
title('Transmisión')
Referencias
Howard Georgi. The physics of waves. Harvard University. February 15, 2015, pp. 218-220. https://www.people.fas.harvard.edu/~hgeorgi/onenew.pdf

