Campo eléctrico producido por una carga puntual Q en el punto P

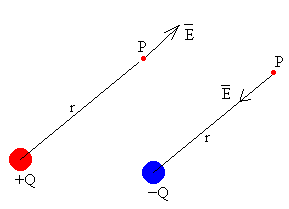
Módulo (cantidad positiva)

${\displaystyle E=\frac{1}{4\pi {\epsilon }_0}\frac{Q}{r^2}}$

Dirección: la recta que pasa por la carga puntual y el punto P

Sentido: Hacia afuera si Q es positiva, hacia la carga si Q es negativa, tal como indican las flechas en la figura.

La unidad de medida del campo en el S.I. de Unidades es el N/C

El potencial producido por una carga puntual Q es una magnitud escalar (positiva o negativa).

${\displaystyle V=\frac{1}{4\pi {\epsilon }_0}\frac{Q}{r}}$

La unidad de medida del potencial en el S.I. de unidades es el volt (V).

Sistema de cargas puntuales

Para hallar el campo eléctrico, en un punto P, producido por una distribución de cargas puntuales, se suma vectorialmente el campo producido por cada una de las cargas en dicho punto P.

${\displaystyle \overrightarrow{E_P}=\overrightarrow{E_1}+\overrightarrow{E_2}+\overrightarrow{E_3}+\mathrm{...}}$

Para hallar el potencial en el punto P, producido por una distribución de cargas puntuales, se suma los potenciales en dicho punto P debidos a cada una de las cargas

${\displaystyle V_P=V_1+V_2+V_3+\mathrm{...}}$

Distribución continua de carga

1. Se calcula el módulo del campo eléctrico producido por un elemento diferencial de carga dq en el punto P
2. Se calcula las componentes dE_x y dE_y de dicho campo
3. Se integra para calcular las componenets E_x y E_y del campo total

Ley de Gauss

El flujo del campo eléctrico $\overrightarrow{E}$ producido por una distribución de carga a través de una superficie cerrada que encirra las cargas q₁, q₂, q₃, .. es

${\displaystyle {{\displaystyle \oint }}^{\text{}}\overrightarrow{E}·\overrightarrow{dS}=\frac{q_1+q_2+q_3+\mathrm{...}}{{\epsilon }_0}}$

Se aplica la ley de Gauss a las siguientes distribuciones de carga:

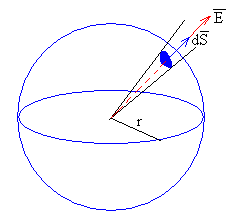
Distribución de carga con simetría esférica.

El campo eléctrico $\overrightarrow{E}$ tiene dirección radial, su módulo es constante en todos los puntos de una superficie esférica concéntrica de radio r.

El flujo del campo eléctrico $\overrightarrow{E}$ a través de dicha superficie es

${\displaystyle {{\displaystyle \oint }}^{\text{}}\overrightarrow{E}·\overrightarrow{dS}={{\displaystyle \oint }}^{\text{}}E·dS·\cos 0=E{{\displaystyle \oint }}^{\text{}}dS=E·4\pi r^2}$

Calculamos la carga q contenida en una superficie esférica de radio r y aplicamos la ley de Gauss

${\displaystyle {{\displaystyle \oint }}^{\text{}}\overrightarrow{E}·\overrightarrow{dS}=\frac{q}{{\epsilon }_0}E=\frac{q}{4\pi {\epsilon }_0{r}^2}}$

Distribución de carga con simetría cilíndrica.

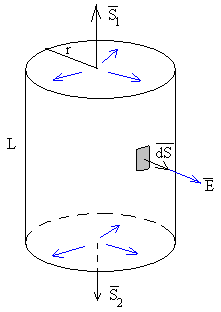
El campo eléctrico tiene dirección radial y perpendicular al eje del cilindro, su módulo es constante en todos los puntos de una superficie cilíndrica de radio r y longitud L.

El flujo del campo eléctrico $\overrightarrow{E}$ a través de dicha superficie es

${\displaystyle \begin{array}{l}{{\displaystyle \oint }}^{\text{}}\overrightarrow{E}·\overrightarrow{dS}=\{\begin{array}{l}\text{s. lateral}{{\displaystyle \int }}^{\text{}}\overrightarrow{E}·\overrightarrow{dS}={{\displaystyle \int }}^{\text{}}E·dS·\cos 0=E{{\displaystyle \int }}^{\text{}}dS=E·2\pi rL\\ \text{base inferior}{{\displaystyle \int }}^{\text{}}\overrightarrow{E}·\overrightarrow{dS}=0\overrightarrow{E}\perp \overrightarrow{S_2}\\ \text{base superior}{{\displaystyle \int }}^{\text{}}\overrightarrow{E}·\overrightarrow{dS}=0\overrightarrow{E}\perp \overrightarrow{S_1}\end{array}\hfill \\ {{\displaystyle \oint }}^{\text{}}\overrightarrow{E}·\overrightarrow{dS}=E·2\pi rL\hfill \end{array}}$

Calculamos la carga q contenida en una superficie cilíndrica de radio r y longitud L y aplicamos la ley de Gauss

${\displaystyle {{\displaystyle \oint }}^{\text{}}\overrightarrow{E}·\overrightarrow{dS}=\frac{q}{{\epsilon }_0}E=\frac{q}{2\pi {\epsilon }_{0}rL}}$

Distribución de carga con simetría plana.

El campo eléctrico $\overrightarrow{E}$ tiene dirección perpendicular al plano cargado. Para calcular el flujo tomamos una superficie cilíndrica cuyo eje es perpendicular al plano cargado y cuya sección es S.

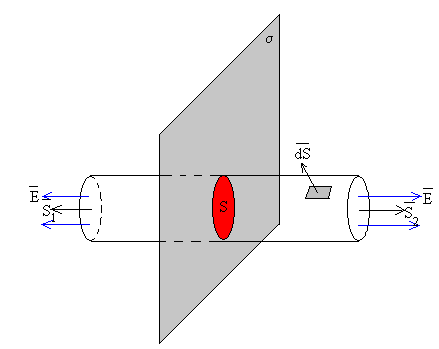
El flujo del campo eléctrico $\overrightarrow{E}$ a través de dicha superficie es

${\displaystyle \begin{array}{l}{{\displaystyle \oint }}^{\text{}}\overrightarrow{E}·\overrightarrow{dS}=\{\begin{array}{l}\text{superficie lateral}{{\displaystyle \int }}^{\text{}}\overrightarrow{E}·\overrightarrow{dS}=0\overrightarrow{E}\perp \overrightarrow{dS}\\ \text{base izquierda}{{\displaystyle \int }}^{\text{}}\overrightarrow{E}·\overrightarrow{dS}=\overrightarrow{E}·\overrightarrow{S_1}=ES\\ \text{base derecha}{{\displaystyle \int }}^{\text{}}\overrightarrow{E}·\overrightarrow{dS}=\overrightarrow{E}·\overrightarrow{S_2}=ES\end{array}\hfill \\ {{\displaystyle \oint }}^{\text{}}\overrightarrow{E}·\overrightarrow{dS}=2E·S\hfill \end{array}}$

Calculamos la carga q contenida en dicha superficie cilíndrica y aplicamos la ley de Gauss

${\displaystyle {{\displaystyle \oint }}^{\text{}}\overrightarrow{E}·\overrightarrow{dS}=\frac{q}{{\epsilon }_0}E=\frac{q}{2S{\epsilon }_0}}$

Diferencia de potencial entre dos puntos

${\displaystyle V_A-V_B={\displaystyle \underset{r_A}{\overset{r_B}{\int }}E·dr}}$

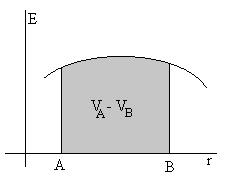
que es el área bajo la curva E-r, tal como se muestra en la figura

Conductores

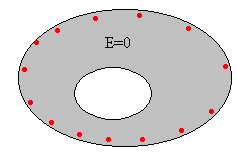
En el interior de un conductor el campo eléctrico es nulo, E=0

Condensadores

Se denomina condensador al dispositivo formado por dos conductores cuyas cargas son iguales pero de signo opuesto.

La capacidad C de un condensador se define como el cociente entre la carga Q y la diferencia de potencia V-V’ existente entre ellos.

${\displaystyle C=\frac{Q}{V-V\text{'}}}$

La unidad de capacidad es el farad o faradio F, aunque se suelen emplear submúltiplos de esta unidad como el microfaradio µF=10^-6 F, y el picofaradio, pF=10^-12 F.

Un condensador acumula una energía U en forma de campo eléctrico.

${\displaystyle U=\frac{1}{2}\frac{Q^2}{C}}$

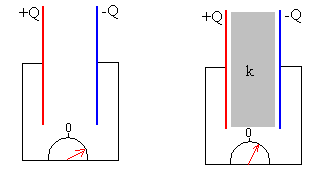
Si introducimos un dieléctrico en un condensador vacío se observa que la diferencia de potencial disminuye. La capacidad C del condensador con dieléctrico es k veces la capacidad del condensador vacío C₀.

C=k·C₀

Movimiento en un campo eléctrico

Una partícula cargada que está en una región donde hay un campo eléctrico, experimenta una fuerza igual al producto de su carga por la intensidad del campo eléctrico $\overrightarrow{F_e}=q·\overrightarrow{E}$ .

• Si la carga es positiva, experimenta una fuerza en el sentido del campo
• Si la carga es negativa, experimenta una fuerza en sentido contrario al campo

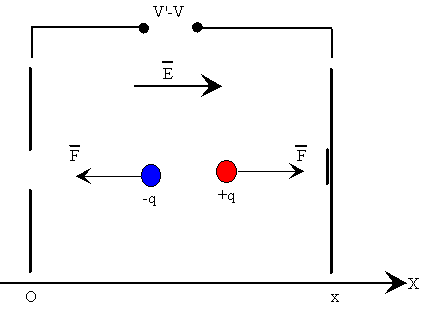
Si el campo es uniforme, la fuerza es constante y también lo es, la aceleración. Aplicando las ecuaciones del movimiento rectilíneo uniformemente acelerado, obtenemos la velocidad de la partícula en cualquier instante o después de haberse desplazado una determinada distancia

${\displaystyle a=\frac{qE}{m}v=v_0+atx=v_{0}t+\frac{1}{2}a{t}^2}$

De forma alternativa, podemos aplicar el principio de conservación de la energía, ya que el campo eléctrico es conservativo

La energía potencial q(V'-V) se transforma en energía cinética. Siendo V'-V la diferencia de potencial existente entre dos puntos distantes x. En un campo eléctrico uniforme V'-V=Ex.

${\displaystyle q(V\text{'}-V)=\frac{1}{2}m{v}^2-\frac{1}{2}m{v}_0^2}$