Campo producido por un hilo rectilíneo cargado

En este apartado, vamos a deducir el campo producido en un punto P distante R, de una línea indefinida cargada con una densidad de λ C/m.

El campo eléctrico tiene simetría cilíndrica, por lo que solamente es necesario considerar un plano que contenga el hilo rectilíneo cargado.

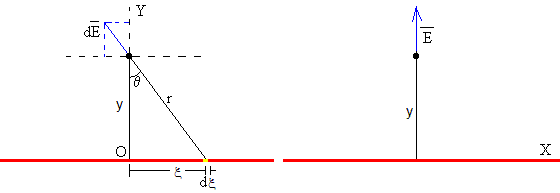
Situamos el origen O en cualquier punto de hilo cargado, el campo producido por el elemento de carga dq, comprendido entre ξ y ξ+dξ, en el punto (0, y) tiene la dirección y el sentido indicado en la figura y su módulo es

${\displaystyle dE=\frac{1}{4\pi {\epsilon }_0}\frac{dq}{r^2}}$

Este campo tiene dos componentes: una a lo largo del eje vertical Y y otra, a lo largo del eje horizontal X.

${\displaystyle d{E}_y=dE\cos \theta }$

La componente horizontal X no es necesario calcularla ya que por simetría se anulan de dos en dos. El elemento de carga dq situado en x y el elemento de carga dq situado en –x producen campos cuyos módulos son iguales y cuyas componentes horizontales son iguales y opuestas. El campo total es la suma de las componentes verticales Y

El campo tiene por dirección la perpendicular a la línea indefinida cargada, tal como se indica en la figura de la derecha.

Campo eléctrico producido por n hilos rectilíneos cargados

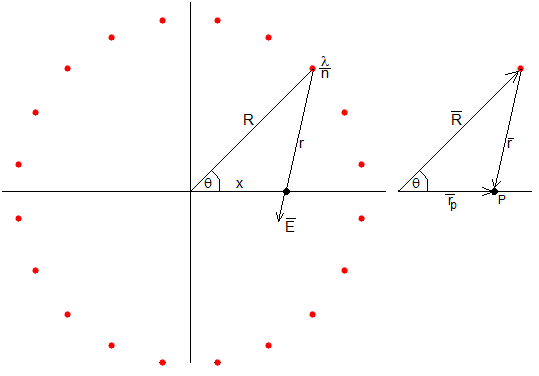
Sean n hilos rectilíneos, cada uno de ellos con una densidad de carga λ/n perpendiculares al plano de la pantalla, situados en una circunferencia de radio R, en las posiciones angulares

${\displaystyle {\theta }_k=2\pi \frac{k-\frac{1}{2}}{n},k=\mathrm{1,2,3,...}n}$

n=20;
R=1;
hold on
for k=1:n
    th=2*pi*(k-1/2)/n;
    plot(R*cos(th),R*sin(th),'ro','markersize',4,'markerfacecolor','r') 
end
hold off
axis equal

Vamos a determinar el campo eléctrico en un punto P situado en el eje X, a una distancia x del origen.

El campo eléctrico producido por un hilo situado en la posición θ en P, es

${\displaystyle \begin{array}{l}E=\frac{\lambda /n}{2\pi {\epsilon }_{0}r}\\ \overrightarrow{r}=\overrightarrow{r_p}-\overrightarrow{R}=\left(x-R\cos \theta \right)\widehat{i}-R\sin \theta \widehat{j}\end{array}}$

Las componentes del campo eléctrico son

${\displaystyle \begin{array}{l}{E}_x=\frac{\lambda }{2\pi {\epsilon }_{0}n}\frac{x-R\cos \theta }{{\left(x-R\cos \theta \right)}^2-{\left(R\sin \theta \right)}^2}\\ E_y=-\frac{\lambda }{2\pi {\epsilon }_{0}n}\frac{R\sin \theta }{{\left(x-R\cos \theta \right)}^2-{\left(R\sin \theta \right)}^2}\end{array}}$

El campo total producido por los n hilos cargados en P, es

${\displaystyle \begin{array}{l}{E}_x=\frac{\lambda }{2\pi {\epsilon }_{0}n}{\displaystyle \sum _{k=1}^n\frac{x-R\cos {\theta }_k}{x^2+R^2-2Rx\cos {\theta }_k}}\\ E_y=-\frac{\lambda }{2\pi {\epsilon }_{0}n}{\displaystyle \sum _{k=1}^n\frac{R\sin {\theta }_k}{x^2+R^2-2Rx\cos {\theta }_k}}\end{array}}$

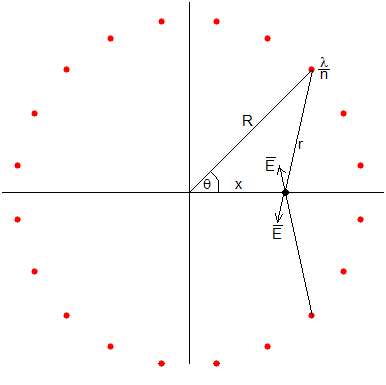
Por simetría, las componentes E_y se anulan de dos en dos tal como se aprecia en la figura. El campo total tiene la dirección del eje X.

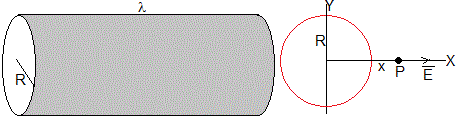
Cuando n es grande, tenemos una superficie cilíndrica de longitud infinita, de radio R, cargada con λ C/m. El campo en el interior es nulo y en el exterior, es

${\displaystyle E=\frac{1}{2\pi {\epsilon }_0}\frac{\lambda }{x}}$

su dirección es radial y perpendicular al eje del cilindro.

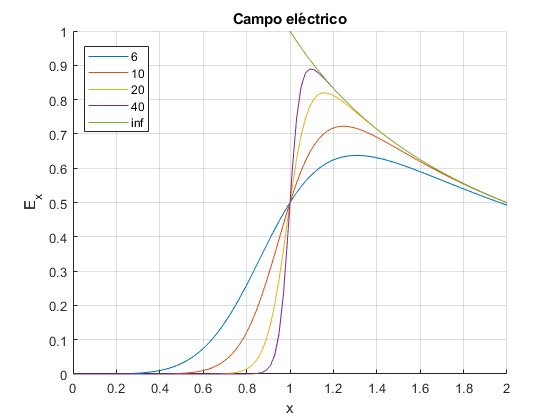
Calculamos el campo eléctrico en los puntos del eje X en el intervalo [0,2], producido por n=6, 10, 20, 40, ∞ hilos rectilíneos situados en una circunferencia de radio R=1. Se ha tomado la constante λ/(2πε₀)=1

R=1; %radio de la circunferencia
xx=linspace(0,2,100); %posición del punto
hold on
for n=[6,10,20,40] %número de hilos
    Ex=zeros(1,length(xx));
    j=1;
    for x=xx
        for k=1:n %n hilos rectilíneos cargados 
            th=2*pi*(k-1/2)/n;
            Ex(j)=Ex(j)+(x-R*cos(th))/(n*(x^2+R^2-2*R*x*cos(th)));
        end
        j=j+1;
    end
    plot(xx,Ex,'displayName',num2str(n))
end
fplot(@(x) 1./x,[1,2],'displayName','inf') %cilindro cargado
hold off
grid on
xlabel('x')
legend('-DynamicLegend','location','best')
ylabel('E_x')
title('Campo eléctrico')

Campo eléctrico y potencial producido por un segmento rectilíneo cargado

Sea una corriente rectilínea finita, de longitud 2l cargada con densidad uniforme λ C/m. Situamos el origen en el punto medio. Debido a la simetría cilíndrica del problema consideramos un plano XY que contiene la línea cargada, tal como semuestra en la figura

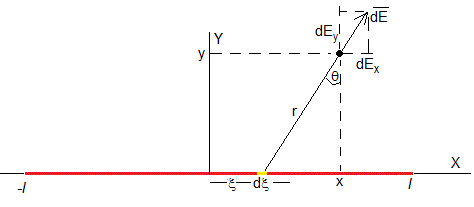
El campo producido por el elemento de carga dq, comprendido entre ξ y ξ+dξ, tiene la dirección y el sentido indicado en la figura y su módulo es

${\displaystyle dE=\frac{1}{4\pi {\epsilon }_0}\frac{dq}{r^2}}$

Este campo tiene dos componentes: una a lo largo del eje vertical Y y otra, a lo largo del eje horizontal X.

${\displaystyle d{E}_x=dE\sin \theta ,d{E}_y=dE\cos \theta }$

Componente X

${\displaystyle E_x=\frac{1}{4\pi {\epsilon }_0}{\displaystyle \underset{-l}{\overset{l}{\int }}\frac{\lambda d\xi }{r^2}\sin \theta }=\frac{1}{4\pi {\epsilon }_0}{\displaystyle \underset{-l}{\overset{l}{\int }}\frac{\lambda d\xi }{r^2}\frac{x-\xi }{r}}=\frac{\lambda }{4\pi {\epsilon }_0}{\displaystyle \underset{-l}{\overset{l}{\int }}\frac{(x-\xi )d\xi }{{\left({\left(x-\xi \right)}^2+y^2\right)}^{3/2}}}}$

Hacemos el cambio de variable, u=x-ξ, du=-dξ, la integral es inmediata

${\displaystyle {\displaystyle \int \frac{(x-\xi )d\xi }{{\left({\left(x-\xi \right)}^2+y^2\right)}^{3/2}}=-}{\displaystyle \int \frac{u·du}{{\left(u^2+y^2\right)}^{3/2}}=\frac{1}{\sqrt{u^2+y^2}}}=\frac{1}{\sqrt{{\left(x-\xi \right)}^2+y^2}}}$

La componente X del campo eléctrico en el punto P (x,y) es

${\displaystyle E_x=\frac{\lambda }{4\pi {\epsilon }_0}{\displaystyle \underset{-l}{\overset{l}{\int }}\frac{(x-\xi )d\xi }{{\left({\left(x-\xi \right)}^2+y^2\right)}^{3/2}}}=\frac{\lambda }{4\pi {\epsilon }_0}\left(\frac{1}{\sqrt{{\left(x-l\right)}^2+y^2}}-\frac{1}{\sqrt{{\left(x+l\right)}^2+y^2}}\right)}$

Para x=0, E_x=0, debido a la simetría

Componente Y

${\displaystyle E_y=\frac{1}{4\pi {\epsilon }_0}{\displaystyle \underset{-l}{\overset{l}{\int }}\frac{\lambda d\xi }{r^2}\cos \theta }=\frac{1}{4\pi {\epsilon }_0}{\displaystyle \underset{-l}{\overset{l}{\int }}\frac{\lambda d\xi }{r^2}\frac{y}{r}}=\frac{\lambda y}{4\pi {\epsilon }_0}{\displaystyle \underset{-l}{\overset{l}{\int }}\frac{d\xi }{{\left({\left(x-\xi \right)}^2+y^2\right)}^{3/2}}}}$

Hacemos el cambio de variable, u=x-ξ, du=-dξ

${\displaystyle {\displaystyle \int \frac{d\xi }{{\left({\left(x-\xi \right)}^2+y^2\right)}^{3/2}}=-}{\displaystyle \int \frac{du}{{\left(u^2+y^2\right)}^{3/2}}=}-\frac{1}{y^3}{\displaystyle \int \frac{du}{{\left({\left(\frac{u}{y}\right)}^2+1\right)}^{3/2}}}}$

Hacemos el cambio de variable

${\displaystyle \frac{u}{y}=\tan \theta ,du=\frac{y}{{\cos }^2\theta }d\theta }$

Utilizamos las relaciones trigonométricas

${\displaystyle {\cos }^2\theta =\frac{1}{1+{\tan }^2\theta },{\sin }^2\theta =\frac{{\tan }^2\theta }{1+{\tan }^2\theta }}$

Integramos y deshacemos los cambios de variable

${\displaystyle \begin{array}{l}-\frac{1}{y^3}{\displaystyle \int \frac{du}{{\left({\left(\frac{u}{y}\right)}^2+1\right)}^{3/2}}}=-\frac{1}{y^2}{\displaystyle \int \cos \theta ·d\theta =-\frac{1}{y^2}\sin \theta =-}\frac{1}{y^2}\frac{\tan \theta }{\sqrt{1+{\tan }^2\theta }}=\\ -\frac{1}{y^2}\frac{u}{\sqrt{u^2+y^2}}=-\frac{1}{y^2}\frac{x-\xi }{\sqrt{{\left(x-\xi \right)}^2+y^2}}\end{array}}$

>> syms a x;
>> int(1/(x^2+a^2)^(3/2),x)
ans =x/(a^2*(a^2 + x^2)^(1/2))

La componente Y del campo eléctrico en el punto P (x,y) es

${\displaystyle E_y=\frac{\lambda y}{4\pi {\epsilon }_0}{\displaystyle \underset{-l}{\overset{l}{\int }}\frac{d\xi }{{\left({\left(x-\xi \right)}^2+y^2\right)}^{3/2}}}=\frac{\lambda }{4\pi {\epsilon }_0}\frac{1}{y}\left(\frac{x+l}{\sqrt{{\left(x+l\right)}^2+y^2}}-\frac{x-l}{\sqrt{{\left(x-l\right)}^2+y^2}}\right)}$

Para x=0, E_x=0, la otra componente E_y vale

${\displaystyle E_y=\frac{\lambda }{2\pi {\epsilon }_0}\frac{l}{y\sqrt{l^2+y^2}}}$

Cuando la longitud l se hace muy grande

${\displaystyle \lim \underset{l\to \infty }{E_y}=\frac{\lambda }{2\pi {\epsilon }_0}\frac{1}{y}}$

Resultado que hemos obtenido en el primer apartado con y=R, distancia del punto P a la línea cargada

Representamos las componentes del campo eléctrico E_x y E_y en función de x para un hilo rectilíneo cargado de longitud 2l=4, para puntos P que distan y=0.5 del hilo

l=2; %longitud del segmento 2l
y=0.5; 
Ex=@(x) 1./sqrt((x-l).^2+y^2)-1./sqrt((x+l).^2+y^2);
Ey=@(x) ((x+l)./sqrt((x+l).^2+y^2)-(x-l)./sqrt((x-l).^2+y^2))/y;
hold on
fplot(Ex,[-2*l,2*l])
fplot(Ey,[-2*l,2*l])
hold off
xlabel('x')
ylabel('E_x,E_y')
legend('E_x','E_y','location','best')
grid on
title('Componentes E_x, E_y')

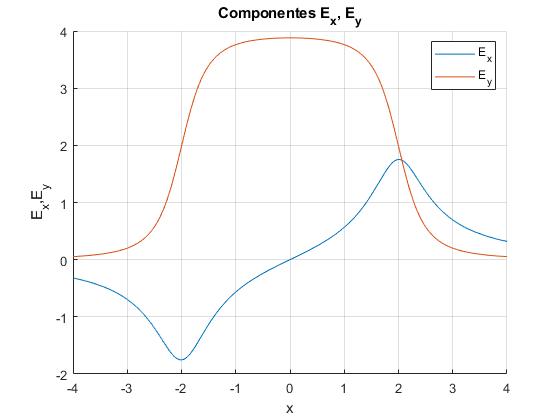
Observamos la simetría de las funciones que describen las componentes E_x y E_y del campo eléctrico. La componte E_y, para una distancia y del hilo cargado al punto, tiende hacia un valor constante cuando la longitud del hilo se hace grande.

Potencial

El potencial en el punto P (x,y) es

${\displaystyle V(x,y)=\frac{1}{4\pi {\epsilon }_0}{\displaystyle \underset{-l}{\overset{l}{\int }}\frac{\lambda d\xi }{r}}=\frac{\lambda }{4\pi {\epsilon }_0}{\displaystyle \underset{-l}{\overset{l}{\int }}\frac{d\xi }{\sqrt{{\left(x-\xi \right)}^2+y^2}}}}$

Hacemos el cambio de variable, u=x-ξ, du=-dξ. Véase la lista de integrales

${\displaystyle {\displaystyle \int \frac{d\xi }{\sqrt{{\left(x-\xi \right)}^2+y^2}}=-}{\displaystyle \int \frac{du}{\sqrt{u^2+y^2}}=-}\ln \left(u+\sqrt{u^2+y^2}\right)=\ln \left((x-\xi )+\sqrt{{\left(x-\xi \right)}^2+y^2}\right)}$

>>  syms a x;
>> int(1/sqrt(x^2+a^2),x)
ans =log(x + (a^2 + x^2)^(1/2))

El potencial en el punto P (x,y) es

${\displaystyle V(x,y)=\frac{\lambda }{4\pi {\epsilon }_0}{\displaystyle \underset{-l}{\overset{l}{\int }}\frac{d\xi }{\sqrt{{\left(x-\xi \right)}^2+y^2}}}=\frac{\lambda }{4\pi {\epsilon }_0}\ln \left(\frac{(x+l)+\sqrt{{\left(x+l\right)}^2+y^2}}{(x-l)+\sqrt{{\left(x-l\right)}^2+y^2}}\right)}$

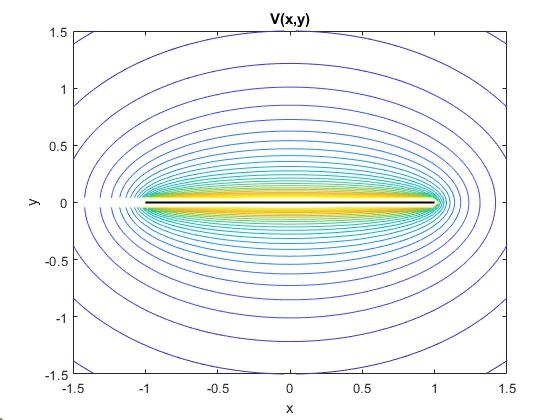
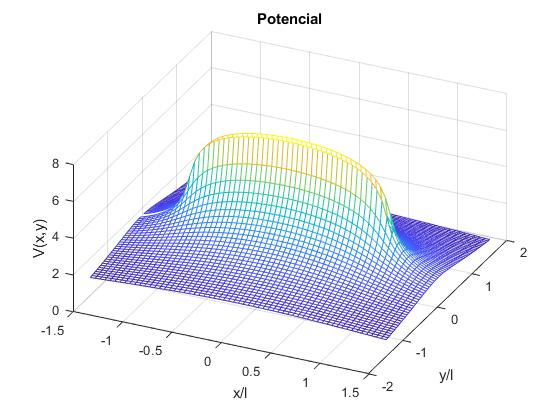
Representamos V(x,y) en función de las variables adimensionales x/l e y/l

f=@(x,y) log((x+1+sqrt((x+1).^2+y.^2))./(x-1+sqrt((x-1).^2+y.^2)));
fcontour(f,[-1.5,1.5,-1.5,1.5], 'LevelStep',0.25)
line([-1,1],[0,0],'lineWidth',1.5,'color','k')
xlabel('x')
ylabel('y')
title('V(x,y)')

[x,y] = meshgrid(-1.5:0.05:1.5, -1.5:0.05:1.5);
f=@(x,y) log((x+1+sqrt((x+1).^2+y.^2))./(x-1+sqrt((x-1).^2+y.^2)));
z=f(x,y);
mesh(x,y,z)
xlabel('x/l')
ylabel('y/l')
zlabel('V(x,y)')
title('Potencial')
view(25,45)

El potencial en un punto P situado en el eje Y, x=0

${\displaystyle V(y)=\frac{\lambda }{4\pi {\epsilon }_0}\ln \left(\frac{\sqrt{l^2+y^2}+l}{\sqrt{l^2+y^2}-l}\right)}$

Campo eléctrico producido por un anillo cargado

En esta sección se calcula el campo eléctrico y el potencial producido por un anillo uniformemente cargado en un punto de su eje de simetría. Aplicaremos el resultado obtenido para calcular el campo y potencial producido por un disco de radio R, uniformemente cargado y finalmente, el campo producido por un plano indefinido, cuando el radio del disco se hace muy grande.

Sin embargo, el campo y el potencial en un punto fuera del eje del anillo requiere el cálculo de integrales elípticas completas de primera y segunda especie.

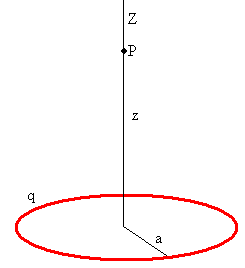
El anillo de radio a contiene una carga q uniformemente distribuida en su longitud.

Potencial producido por el anillo en un punto z de su eje de simetría

La carga q dista r del punto P, luego el potencial es

${\displaystyle V=\frac{1}{4\pi {\epsilon }_0}\frac{q}{\sqrt{a^2+z^2}}}$

Campo eléctrico producido por el anillo en un punto de su eje de simetría

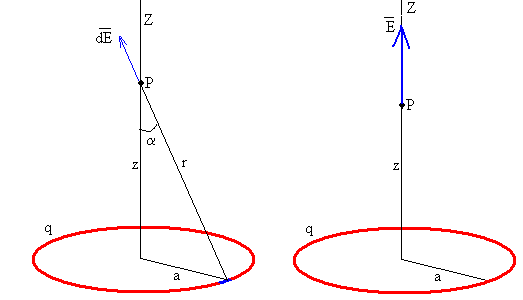
El campo producido por el elemento de carga dq en el punto P vale

${\displaystyle \frac{1}{4\pi {\epsilon }_0}\frac{dq}{r^2}}$

Por simetría, las componentes de dicho campo perpendiculares al eje de simetría correspondientes a dos elementos de carga diametralmente opuestos se anulan.

El campo total es paralelo al eje Z de simetría y vale

${\displaystyle \begin{array}{l}E={\displaystyle \oint \frac{1}{4\pi {\epsilon }_0}\frac{dq}{r^2}\cos \alpha }=\frac{1}{4\pi {\epsilon }_0}\frac{q}{a^2+z^2}\frac{z}{\sqrt{a^2+z^2}}=\\ \frac{1}{4\pi {\epsilon }_0}\frac{qz}{{\left(a^2+z^2\right)}^{3/2}}\end{array}}$

El campo también se puede obtener a partir del potencial

${\displaystyle E=-\frac{dV}{dz}=\frac{1}{4\pi {\epsilon }_0}\frac{qz}{{(a^2+z^2)}^{3/2}}}$

Representamos el campo eléctrico en función de x=z/a

f=@(x) x./(1+x.^2).^(3/2);
fplot(f,[0,5])
line([1/sqrt(2),1/sqrt(2)],[0,2/sqrt(27)],'lineStyle','--') %máximo
grid on
xlabel('z/a')
ylabel('E')
title('Anillo cargado')

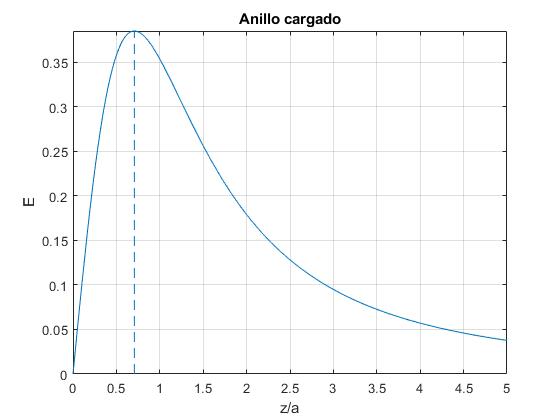
El campo E alcanza su valor máximo para z_m tal que, la derivada es nula

${\displaystyle \begin{array}{l}\begin{array}{l}\frac{dE}{dz}=\frac{q}{4\pi {\epsilon }_0}\frac{{(a^2+z^2)}^{3/2}-\frac{3}{2}2z^2{(a^2+z^2)}^{1/2}}{{\left(a^2+z^2\right)}^3}=0\hfill \\ a^2-2z^2=\mathrm{0,}{z}_m=\pm \frac{a}{\sqrt{2}}\hfill \end{array}\\ E_m=\frac{2}{\sqrt{27}}\frac{q}{4\pi {\epsilon }_0{a}^2}\end{array}}$

Disco uniformemente cargado

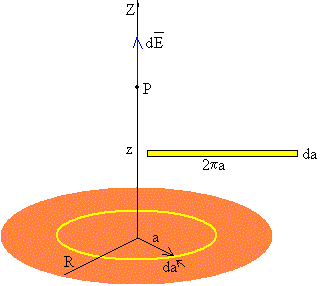
Consideremos un disco de radio R, uniformemente cargado con una densidad de carga σ C/m²

El potencial producido en P por el anillo cargado de radio a y anchura da, , que contiene una carga dq=σ·2πa·da, es

${\displaystyle dV=\frac{1}{4\pi {\epsilon }_0}\frac{dq}{\sqrt{a^2+z^2}}=\frac{\sigma }{2{\epsilon }_0}\frac{a·da}{\sqrt{a^2+z^2}}}$

El potencial del disco cargado es

${\displaystyle V=\frac{\sigma }{2{\epsilon }_0}{\displaystyle \underset{0}{\overset{R}{\int }}\frac{a·da}{\sqrt{a^2+z^2}}}=\frac{\sigma }{2{\epsilon }_0}\left(\sqrt{R^2+z^2}-\left|z\right|\right)}$

Es el mismo por encima z>0 y por debajo z<0 del disco

Para z=0 (centro del disco) el potencial es

${\displaystyle V(0)=\frac{\sigma R}{2{\epsilon }_0}}$

Campo eléctrico

El campo dE producido por un anillo de radio a y de anchura daes

${\displaystyle dE=\frac{1}{4\pi {\epsilon }_0}\frac{z·dq}{{\left(a^2+z^2\right)}^{3/2}}=\frac{1}{4\pi {\epsilon }_0}\frac{z·\sigma ·2\pi a·da}{{\left(a^2+z^2\right)}^{3/2}}}$

El campo total producido por el disco cargado es la suma de los campos producidos por todos los anillos que forman el disco.

${\displaystyle E={\displaystyle \underset{0}{\overset{R}{\int }}\frac{1}{4\pi {\epsilon }_0}\frac{z·\sigma ·2\pi a·da}{{\left(a^2+z^2\right)}^{3/2}}=}\frac{\pi z·\sigma }{4\pi {\epsilon }_0}{\displaystyle \underset{0}{\overset{R}{\int }}\frac{2a·da}{{\left(a^2+z^2\right)}^{3/2}}}=\frac{\sigma }{2{\epsilon }_0}\left(1-\frac{z}{\sqrt{R^2+z^2}}\right)}$

Para un plano indefinido cargado R→∞

${\displaystyle E=\frac{\sigma }{2{\epsilon }_0}}$

El mismo resultado se obtiene aplicando la ley de Gauss.

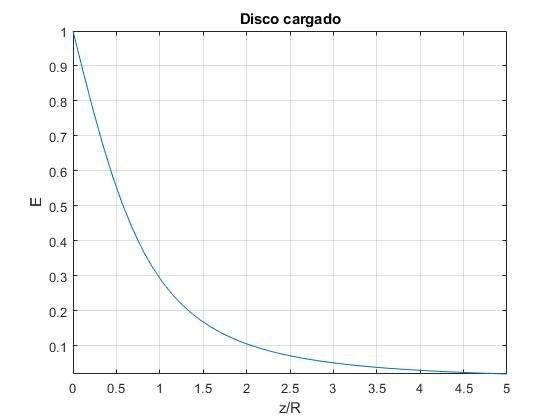
Representamos el campo eléctrico en función de x=z/R

f=@(x) 1-x./sqrt(1+x.^2);
fplot(f,[0,5])
grid on
xlabel('z/R')
ylabel('E')
title('Disco cargado')

El campo eléctrico producido por un disco de radio x en un punto P es

${\displaystyle \begin{array}{l}{E}_{\uparrow }=\frac{\sigma }{2{\epsilon }_0}\left(1-\frac{r-z}{\sqrt{x^2+{\left(r-z\right)}^2}}\right)=\frac{1}{2{\epsilon }_0}\frac{q}{\pi x^2}\left(1-\frac{r-z}{\sqrt{x^2+{\left(r-z\right)}^2}}\right),r>z\\ E_{\downarrow }=\frac{1}{2{\epsilon }_0}\frac{q}{\pi x^2}\left(1-\frac{z-r}{\sqrt{x^2+{\left(z-r\right)}^2}}\right),r<z\end{array}}$

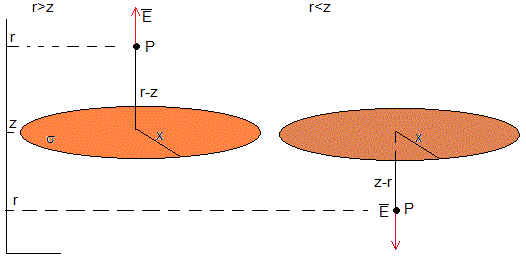
donde q es la carga del disco. Aplicaremos estas expresiones en los dos casos que se describen a continuación

Campo eléctrico producido por un cilindro uniformemente cargado en un punto de su eje

Consideremos un cilindro de radio R y longitud 2L uniformemente cargado con ρ C/m³

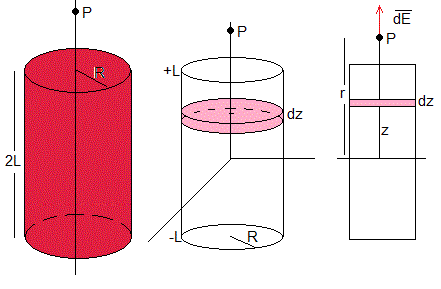
Dividimos el cilindro en discos de radio R y espesor dz. El volumen del disco es πR²dz, la carga que contiene es dq=ρ·πR²dz

• r≥L

El campo eléctrico producido en P por un disco situado en z, es

${\displaystyle dE=\frac{1}{2{\epsilon }_0}\frac{\rho \left(\pi R^2·dz\right)}{\pi R^2}\left(1-\frac{r-z}{\sqrt{R^2+{(r-z)}^2}}\right)=\frac{\rho }{2{\epsilon }_0}\left(1-\frac{r-z}{\sqrt{R^2+{(r-z)}^2}}\right)dz}$

Integramos desde -L a +L

${\displaystyle \begin{array}{l}E=\frac{\rho }{2{\epsilon }_0}{\displaystyle \underset{-L}{\overset{L}{\int }}\left(1-\frac{r-z}{\sqrt{R^2+{(r-z)}^2}}\right)dz=}\frac{\rho }{2{\epsilon }_0}{\left(z+\sqrt{R^2+{(r-z)}^2}\right)|}_{-L}^L=\\ \frac{\rho }{2{\epsilon }_0}\left(2L+\sqrt{R^2+{(r-L)}^2}-\sqrt{R^2+{(r+L)}^2}\right)\end{array}}$

• r≤L



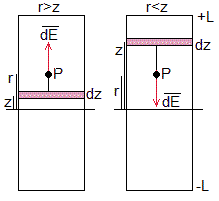
Los discos por debajo de P, comprendidos entre -L y r, producen un campo eléctrico cuya dirección es el eje Z y sentido positivo (hacia arriba) como en el apartado anterior

${\displaystyle \begin{array}{l}{E}_{\uparrow }=\frac{\rho }{2{\epsilon }_0}{\displaystyle \underset{-L}{\overset{r}{\int }}\left(1-\frac{r-z}{\sqrt{R^2+{\left(r-z\right)}^2}}\right)dz}\\ E_{\uparrow }=\frac{\rho }{2{\epsilon }_0}\left(r+L+R-\sqrt{R^2+{\left(r+L\right)}^2}\right)\end{array}}$

Los discos por encima de P entre r y L, producen un campo eléctrico que tiene la misma dirección pero sentido contrario

${\displaystyle \begin{array}{l}{E}_{\downarrow }=\frac{\rho }{2{\epsilon }_0}{\displaystyle \underset{r}{\overset{L}{\int }}\left(1-\frac{z-r}{\sqrt{R^2+{\left(z-r\right)}^2}}\right)dz=}\frac{\rho }{2{\epsilon }_0}{\left(z-\sqrt{R^2+{\left(r-z\right)}^2}\right)|}_r^L\\ E_{\downarrow }=\frac{\rho }{2{\epsilon }_0}\left(L-r-\sqrt{R^2+{\left(L-r\right)}^2}+R\right)\end{array}}$

El campo eléctrico en P es la diferencia

${\displaystyle E=E_{\uparrow }-E_{\downarrow }=\frac{\rho }{2{\epsilon }_0}\left(2r+\sqrt{R^2+{\left(L-r\right)}^2}-\sqrt{R^2+{\left(r+L\right)}^2}\right)}$

Cuando r=0, E=0

Campo en el interior y en el exterior de una esfera uniformemente cargada

Campo eléctrico en un punto exterior P distante r del centro de la esfera

Supondremos una esfera de radio R uniformemente cargada con ρ C/m³

Dividimos la esfera en discos de radio x y espesor dz. El volumen del disco es πx²dz, la carga que contiene es dq=ρ·πx²dz

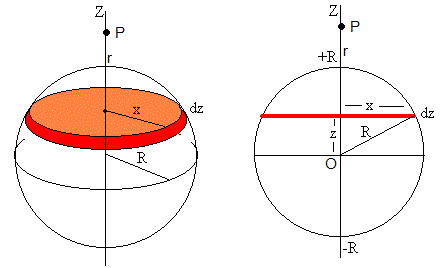
El campo eléctrico producido en P por un disco situado en z, de radio x y de espesor dz es

${\displaystyle \begin{array}{l}dE=\frac{1}{2{\epsilon }_0}\frac{\rho \pi x^2·dz}{\pi x^2}\left(1-\frac{r-z}{\sqrt{x^2+{\left(r-z\right)}^2}}\right)=\frac{\rho }{2{\epsilon }_0}\left(1-\frac{r-z}{\sqrt{x^2+{\left(r-z\right)}^2}}\right)dz\\ dE=\frac{\rho }{2{\epsilon }_0}\left(1-\frac{r-z}{\sqrt{R^2+r^2-2rz}}\right)dz\end{array}}$

Como vemos en la parte derecha de la figura x²=R²-z²

El campo eléctrico producido por todos los discos en los que se ha dividido la esfera tiene la misma dirección y sentido. El campo total es

${\displaystyle E=\frac{\rho }{2{\epsilon }_0}{\displaystyle \underset{-R}{\overset{R}{\int }}\left(1-\frac{r}{\sqrt{R^2+r^2-2rz}}+\frac{z}{\sqrt{R^2+r^2-2rz}}\right)dz}}$

Las integrales de los dos primeros términos son inmediatas. Resolvemos por partes la integral del tercer término

${\displaystyle \begin{array}{l}\{\begin{array}{l}u=z\\ dv=\frac{dz}{\sqrt{R^2+r^2-2rz}}\end{array}\{\begin{array}{l}du=dz\\ v=-\frac{\sqrt{R^2+r^2-2rz}}{r}\end{array}\\ {\displaystyle \int \frac{z}{\sqrt{R^2+r^2-2rz}}dz=}-\frac{z}{r}\sqrt{R^2+r^2-2rz}+\frac{1}{r}{\displaystyle \int \sqrt{R^2+r^2-2rz}·dz}=\\ -\frac{z}{r}\sqrt{R^2+r^2-2rz}-\frac{{\left(R^2+r^2-2rz\right)}^{3/2}}{3r^2}\end{array}}$

El campo eléctrico en P producido por la esfera cargada es

${\displaystyle \begin{array}{l}E=\frac{\rho }{2{\epsilon }_0}{\left\{z+\sqrt{R^2+r^2-2rz}-\frac{z}{r}\sqrt{R^2+r^2-2rz}-\frac{{\left(R^2+r^2-2rz\right)}^{3/2}}{3r^2}\right\}}_{-R}^R\\ E=\frac{\rho }{2{\epsilon }_0}\left\{\frac{2R^2}{r}+\frac{{\left(r+R\right)}^3-{\left(r-R\right)}^3}{3r^2}\right\}=\frac{\rho R^3}{3{\epsilon }_0}\frac{1}{r^2}\end{array}}$

El mismo resultado que se obtiene aplicando la ley de Gauss a una esfera uniformemente cargada con una carga $q=\rho \frac{4}{3}\pi R^3$

Campo eléctrico en un punto interior P distante r del centro de la esfera

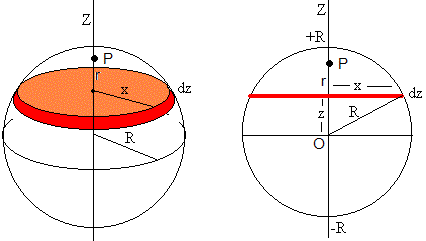
Los discos por debajo de P, comprendidos entre -R y r, producen un campo eléctrico cuya dirección es el eje Z y sentido positivo (hacia arriba) como en el apartado anterior, su módulo es

${\displaystyle dE=\frac{\rho }{2{\epsilon }_0}\left(1-\frac{r-z}{\sqrt{R^2+r^2-2rz}}\right)dz}$

El campo eléctrico hacia arriba es

${\displaystyle \begin{array}{l}{E}_{\uparrow }=\frac{\rho }{2{\epsilon }_0}{\displaystyle \underset{-R}{\overset{r}{\int }}\left(1-\frac{r}{\sqrt{R^2+r^2-2rz}}+\frac{z}{\sqrt{R^2+r^2-2rz}}\right)dz=}\\ \frac{\rho }{2{\epsilon }_0}{\left\{z+\sqrt{R^2+r^2-2rz}-\frac{z}{r}\sqrt{R^2+r^2-2rz}-\frac{{\left(R^2+r^2-2rz\right)}^{3/2}}{3r^2}\right\}}_{-R}^r\\ E_{\uparrow }=\frac{\rho }{2{\epsilon }_0}\left\{-\frac{R^2}{r}-R+\frac{{\left(r+R\right)}^3-{\left(R-r\right)}^{3/2}}{3r^2}\right\}\end{array}}$

Los discos por encima de P entre r y R, producen un campo eléctrico que tiene la misma dirección pero sentido contrario, su módulo es

${\displaystyle dE=\frac{\rho }{2{\epsilon }_0}\left(1-\frac{z-r}{\sqrt{R^2+r^2-2rz}}\right)dz}$

El campo eléctrico hacia abajo es

${\displaystyle \begin{array}{l}{E}_{\downarrow }=\frac{\rho }{2{\epsilon }_0}{\displaystyle \underset{r}{\overset{R}{\int }}\left(1-\frac{z}{\sqrt{R^2+r^2-2rz}}+\frac{r}{\sqrt{R^2+r^2-2rz}}\right)dz}\\ \frac{\rho }{2{\epsilon }_0}{\left\{z+\frac{z}{r}\sqrt{R^2+r^2-2rz}+\frac{{\left(R^2+r^2-2rz\right)}^{3/2}}{3r^2}-\sqrt{R^2+r^2-2rz}\right\}}_r^R\\ E_{\downarrow }=\frac{\rho }{2{\epsilon }_0}\left\{\frac{R^2}{r}-R+\frac{{\left(R-r\right)}^3-{\left(R^2-r^2\right)}^{3/2}}{3r^2}\right\}\end{array}}$

El campo eléctrico en P producido por la esfera cargada, es la diferencia

${\displaystyle E=E_{\uparrow }-E_{\downarrow }=\frac{\rho }{2{\epsilon }_0}\left\{-\frac{2R^2}{r}+\frac{{\left(R+r\right)}^3-{\left(R-r\right)}^3}{3r^2}\right\}=\frac{\rho }{3{\epsilon }_0}r}$

El mismo resultado que se obtiene aplicando la ley de Gauss a una esfera uniformemente cargada con una carga $q=\rho \frac{4}{3}\pi R^3$

Referencias

Nam H. Nguyen, Quy C. Tran, Thach A. Nguyen, Trung V. Phan. The Effect of Charge Discretization on the Electrical Field Inside a Conductor. The Physics Teacher. Vol. 62, January 2024. pp. 29-31