Cuando varias cargas están presentes el campo eléctrico resultante es la suma vectorial de los campos eléctricos producidos por cada una de las cargas. Consideremos el sistema de dos cargas eléctricas de la figura.

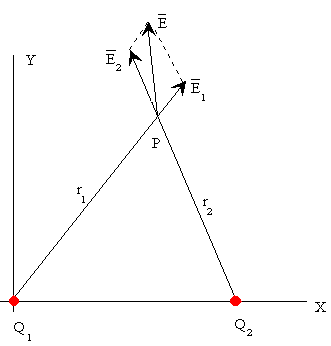
El módulo del campo eléctrico producido por cada una de las cargas es

${\displaystyle E_1=\frac{1}{4\pi {\epsilon }_0}\frac{Q_1}{r_1^2}{E}_2=\frac{1}{4\pi {\epsilon }_0}\frac{Q_{21}}{r_2^2}}$

Y las componentes del campo total son

${\displaystyle \begin{array}{l}{E}_x=E_{1x}+E_{2x}=E_1\cos {\theta }_1+E_2\cos {\theta }_2\\ E_y=E_{1y}+E_{2y}=E_1\sin {\theta }_1+E_2\sin {\theta }_2\end{array}}$

Líneas de fuerza

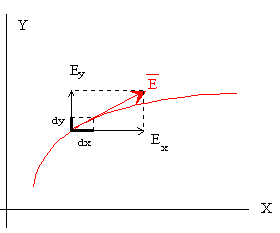
Como el campo es tangente a las líneas de fuerza, la ecuación de las líneas de fuerza es

${\displaystyle \frac{dy}{dx}=\frac{E_y}{E_x}}$

tal como se muestra en la figura.

Equipotenciales

El potencial en el punto P debido a las dos cargas es la suma de los potenciales debidos a cada una de las cargas en dicho punto.

${\displaystyle V=\frac{1}{4\pi {\epsilon }_0}\frac{Q_1}{r_1}+\frac{1}{4\pi {\epsilon }_0}\frac{Q_2}{r_2}}$

Las superficies equipotenciales cortan perpendicularmente a las líneas de campo. Representaremos la intersección de las superficies equipotenciales con el plano XY.

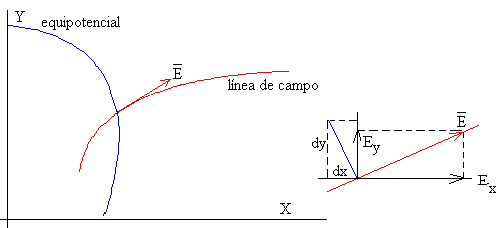
La ecuación de las líneas equipotenciales es

${\displaystyle \frac{dx}{dy}=-\frac{E_y}{E_x}}$

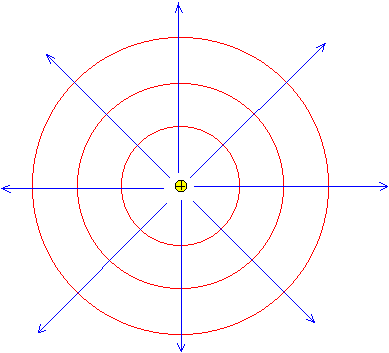
En el caso de una carga puntual. Las líneas de fuerza son rectas que parten del origen y las equipotenciales son superficies eféricas concéntricas, tal como se muestra en la figura

Actividades

Se introduce

• la carga Q₁ se ha fijado en una unidad
• la carga Q₂ en el control titulado Q2

Se pulsa en el botón titulado Nuevo

Observar las líneas de fuerza (en color blanco) y las equipotenciales (en color azul claro) de este sistema de dos cargas.

Obtener el mapa de las líneas de fuerza y equipotenciales de:

• Dos cargas iguales y del mismo signo
• Dos cargas iguales y de distinto signo
• Dos cargas distintas y del mismo signo
• Dos cargas distintas y de distinto signo

El dipolo eléctrico

Un dipolo eléctrico está formado por dos cargas, una positiva +Q y otra negativa -Q del mismo valor, separadas una distancia d.

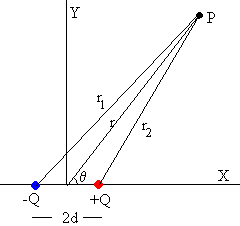
El potencial en el punto P distante r₁ de la carga –Q y r₂ de la carga +Q es

${\displaystyle V=\frac{Q}{4\pi {\epsilon }_0}\left(\frac{1}{r_2}-\frac{1}{r_1}\right)}$

Expresamos r₁ y r₂ en función de r y θ, que es la posición del punto P expresada en coordenadas polares.

${\displaystyle \begin{array}{l}{r}_1^2=r^2+d^2+2rd\cos \theta \\ r_2^2=r^2+d^2-2rd\cos \theta \end{array}}$

Teniendo en cuenta que d es pequeño frente a r, obtenemos una buena aproximación empleando el desarrollo en serie

${\displaystyle {\left(1+x\right)}^{-1/2}=1-\frac{1}{2}x+\frac{3}{8}{x}^2-\mathrm{...}}$

para expresar de forma aproximada los cocientes r/r₁ y r/r₂.

${\displaystyle \frac{r}{r_1}={\left(1+\frac{d^2}{r^2}+\frac{2d}{r}\cos \theta \right)}^{\frac{-1}{2}}\approx 1-\frac{1}{2}\left(\frac{d^2}{r^2}+\frac{2d}{r}\cos \theta \right)+\frac{3}{8}{\left(\frac{d^2}{r^2}+\frac{2d}{r}\cos \theta \right)}^2+\mathrm{...}}$

Despreciando los términos de orden superior a d²/r²

${\displaystyle \begin{array}{l}\frac{r}{r_1}\approx 1-\frac{d}{r}\cos \theta +\frac{d^2}{2r^2}\left(3{\cos }^2\theta -1\right)\\ \frac{r}{r_2}\approx 1+\frac{d}{r}\cos \theta +\frac{d^2}{2r^2}\left(3{\cos }^2\theta -1\right)\end{array}}$

El potencial se expresa en función de r y θ

${\displaystyle V=\frac{Q}{4\pi {\epsilon }_{0}r}\left(\frac{r}{r_2}-\frac{r}{r_1}\right)\approx \frac{2Qd}{4\pi {\epsilon }_0{r}^2}\cos \theta }$

Es interesante destacar, que el potencial debido a un dipolo disminuye con la inversa del cuadrado de la distancia r, mientras que para una carga puntual disminuye con la inversa de r.

Componentes del campo eléctrico

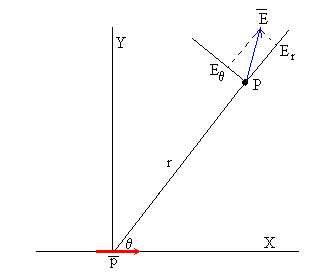
Las componentes de $\overrightarrow{E}$ en coordenadas polares se pueden calcular a partir del gradiente de V expresado en coordenadas polares

${\displaystyle \overrightarrow{E}=-\frac{\partial V}{\partial r}\widehat{r}-\frac{1}{r}\frac{\partial V}{\partial \theta }\widehat{\theta }}$

Las componentes del campo eléctrico $\overrightarrow{E}$ son

${\displaystyle \begin{array}{l}{E}_r=\frac{1}{4\pi {\epsilon }_0}\frac{4Qd}{r^3}\cos \theta \\ E_{\theta }=\frac{1}{4\pi {\epsilon }_0}\frac{2Qd}{r^3}\sin \theta \end{array}}$

La intensidad del campo eléctrico disminuye como el cubo de la distancia r.

Definimos momento dipolar al vector $\overrightarrow{p}$, cuyo módulo es p=Q·2d, el producto de la carga Q por la separación 2d, y que se dirige desde la carga negativa a la positiva.

${\displaystyle \begin{array}{l}{E}_r=\frac{1}{4\pi {\epsilon }_0}\frac{2p}{r^3}\cos \theta \hfill \\ E_{\theta }=\frac{1}{4\pi {\epsilon }_0}\frac{p}{r^3}\sin \theta \hfill \end{array}}$

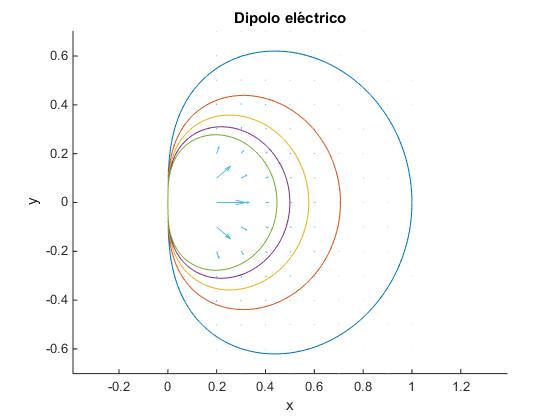
Utilizamos MATLAB para representar las líneas equipotenciales, pero es difícil representar los vectores campo eléctrico en diversos puntos ya que disminuye rápidamente con la distancia al dipolo

hold on
%equipotenciales 
for V=1:5
    ang=(-90:1:90)*pi/180;
    r=sqrt(cos(ang)/V);
    x=r.*cos(ang);
    y=r.*sin(ang);
    plot(x,y);
end
%campo eléctrico  en los puntos de esta malla
[X,Y]=meshgrid(0.2:0.1:1,-0.7:0.1:0.7);
r=sqrt(X.^2+Y.^2);
ang=atan(Y./X);
Er=2*cos(ang)./r.^3; %componentes polares
Ea=sin(ang)./r.^3;
Ex=Er.*cos(ang)-Ea.*sin(ang); %componentes rectangulares
Ey=Er.*sin(ang)+Ea.*cos(ang);
quiver(X,Y,Ex,Ey)
hold off
axis equal
xlabel('x')
ylabel('y')
title('Dipolo eléctrico')

Actividades

Se pulsa el botón titulado Nuevo.

Se observa las líneas de fuerza (en color blanco) y las equipotenciales (en color azul claro) de un dipolo.

Las equipotenciales se han trazado de modo que su separación es de 10 unidades arbitrarias de energía potencial.

Las líneas de fuerza y equipotenciales son similares a las obtenidas en para el sistema de dos cargas, cuando las cargas son iguales y opuestas.

El cuadripolo

Un cuadripolo es un sistema formado por tres cargas +2Q en el origen y –Q en los puntos (-d, 0) y (+d, 0).

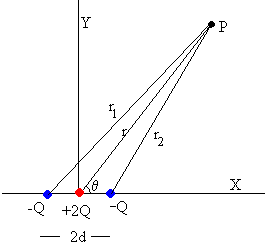
El potencial en el punto P distante r₁ de la carga –Q, r₂ de la carga –Q y r de la carga +2Q es

${\displaystyle \begin{array}{l}V=\frac{Q}{4\pi {\epsilon }_0}\left(\frac{2}{r}-\frac{1}{r_2}-\frac{1}{r_1}\right)\\ r_1=r{\left(1+\frac{2d}{r}\cos \theta +\frac{d^2}{r^2}\right)}^{\frac{1}{2}}\\ r_2=r{\left(1-\frac{2d}{r}\cos \theta +\frac{d^2}{r^2}\right)}^{\frac{1}{2}}\end{array}}$

Como r>>d expresamos de forma aproximada los cocientes r/r₁ y r/r₂.

${\displaystyle \begin{array}{l}\frac{r}{r_1}\approx 1-\frac{d}{r}\cos \theta +\frac{d^2}{2r^2}\left(3{\cos }^2\theta -1\right)\\ \frac{r}{r_2}\approx 1+\frac{d}{r}\cos \theta +\frac{d^2}{2r^2}\left(3{\cos }^2\theta -1\right)\end{array}}$

El potencial se expresa en función de r y θ

${\displaystyle \begin{array}{l}V=\frac{Q}{4\pi {\epsilon }_0}\frac{1}{r}\left(2-\frac{r}{r_1}-\frac{r}{r_2}\right)\approx \\ \frac{Q}{4\pi {\epsilon }_{0}r}\left(2-\left[1-\frac{d}{r}\cos \theta +\frac{1}{2}(3{\cos }^2\theta -1)\frac{d^2}{r^2}+1+\frac{d}{r}\cos \theta +\frac{1}{2}(3{\cos }^2\theta -1)\frac{d^2}{r^2}\right]\right)\\ V\approx \frac{Q}{4\pi {\epsilon }_0}\frac{d^2}{r^3}(3{\cos }^2\theta -1)\end{array}}$

Utilizamos MATLAB para trazar las líneas equipotenciales, de modo similar al dipolo

hold on
for V=1:5
    ang=(0:1:360)*pi/180;
    z=(3*cos(ang).^2-1)/V;
    r=nthroot(z,3);
    x=r.*cos(ang);
    y=r.*sin(ang);
    plot(x,y);
end
xlabel('x')
ylabel('y')
title('Cuadripolo eléctrico')
axis equal

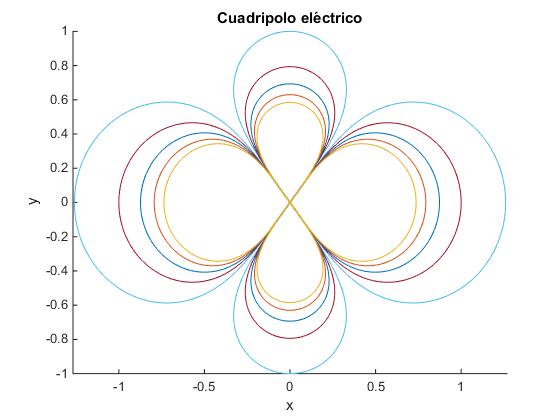
Es interesante destacar, que el potencial debido a un cuadripolo disminuye con la inversa del cubo de la distancia r, mientras que para un dipolo disminuye como la inversa del cuadrado y para una carga puntual disminuye con la inversa de r.

Las componentes del campo eléctrico $\overrightarrow{E}$ son

${\displaystyle \begin{array}{l}{E}_r=-\frac{\partial V}{\partial r}=\frac{1}{4\pi {\epsilon }_0}\frac{3Q{d}^2}{r^4}(3{\cos }^2\theta -1)\\ E_{\theta }=-\frac{1}{r}\frac{\partial V}{\partial \theta }=\frac{1}{4\pi {\epsilon }_0}\frac{3Q{d}^2}{r^4}\sin (2\theta )\end{array}}$

Actividades

Observar las líneas de campo (en color blanco) y las equipotenciales (en color azul claro) de un cuadripolo.

Las equipotenciales se han trazado de modo que su separación es de 10 unidades arbitrarias de energía potencial.