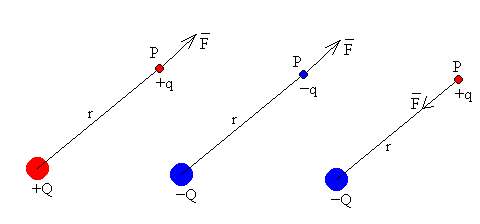
La fuerza que ejerce la carga Q sobre otra carga q situada a una distancia r es.

${\displaystyle \overrightarrow{F}=\frac{1}{4\pi {\epsilon }_0}\frac{Qq}{r^2}\widehat{r}}$

La fuerza es repulsiva si las cargas son del mismo signo y es atractiva si las cargas son de signo contrario.

Energía potencial

La fuerza de atracción entre dos masas es conservativa, del mismo modo se puede demostrar que la fuerza de interacción entre cargas es conservativa.

El trabajo de una fuerza conservativa, es igual a la diferencia entre el valor inicial y el valor final de una función que solamente depende de las coordenadas que denominamos energía potencial.

${\displaystyle \underset{A}{\overset{B}{{\displaystyle \int }}}\overrightarrow{F}·\overrightarrow{dl}=E_{pA}-E_{pB}}$

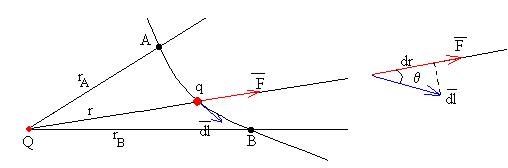
El trabajo infinitesimal es el producto escalar del vector fuerza por el vector desplazamiento, tangente a la trayectoria.

${\displaystyle \overrightarrow{F}·\overrightarrow{dl}=F·dl·\cos \theta =F·dr}$

donde dr es el desplazamiento infinitesimal de la partícula cargada q en la dirección radial.

Para calcular el trabajo total, integramos entre la posición inicial A, distante r_A del centro de fuerzas y la posición final B, distante r_B del centro fijo de fuerzas.

${\displaystyle W={\displaystyle \underset{A}{\overset{B}{\int }}\frac{1}{4\pi {\epsilon }_0}\frac{Qq}{r^2}dr=}{-\frac{1}{4\pi {\epsilon }_0}\frac{Qq}{r}|}_A^B=\frac{1}{4\pi {\epsilon }_0}\frac{Qq}{r_A}-\frac{1}{4\pi {\epsilon }_0}\frac{Qq}{r_B}}$

El trabajo W no depende del camino seguido por la partícula para ir desde la posición A a la posición B. La fuerza de repulsión $\overrightarrow{F}$ , que ejerce la carga fija Q sobre la carga q es conservativa. La fórmula de la energía potencial es

${\displaystyle E_p=\frac{1}{4\pi {\epsilon }_0}\frac{Qq}{r}}$

El nivel cero de energía potencial se ha establecido en el infinito, para r=∞, E_p=0

El hecho de que la fuerza de atracción sea conservativa, implica que la energía total (cinética más potencial) de la partícula es constante, en cualquier punto de la trayectoria.

${\displaystyle E=\frac{1}{2}m{v}^2+E_p=\text{cte}}$

Movimiento de una partícula cargada

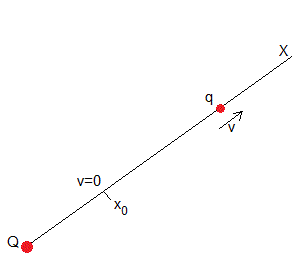
Consideremos una carga Q fija en el origen del eje X. Una partícula de masa m y carga q del mismo signo que Q se sitúa a una distancia x₀, tal como se muestra en la figura. Problemas similares se estudian en la página titulada Movimiento de dos cuerpos bajo la fuerza de atracción mutua

Vamos a estudiar el movimiento de la partícula bajo la fuerza de repulsión eléctrica entre ambas cargas. La energía inicial de la partícula es

${\displaystyle E=\frac{1}{4\pi {\epsilon }_0}\frac{Qq}{x_0}}$

La energía de la partícula cuando se encuentra en la posición x>x₀ y lleva una velocidad v es

${\displaystyle E=\frac{1}{2}m{v}^2+\frac{1}{4\pi {\epsilon }_0}\frac{Qq}{x}}$

La partícula se mueve bajo la acción de una fuerza conservativa, por lo que la energía total permanece constante

${\displaystyle \begin{array}{l}\frac{1}{2}m{\left(\frac{dx}{dt}\right)}^2=\frac{Qq}{4\pi {\epsilon }_0}\left(\frac{1}{x_0}-\frac{1}{x}\right)\\ \frac{dx}{dt}=K\sqrt{\frac{x-x_0}{x}}K=\sqrt{\frac{2Qq}{4\pi {\epsilon }_{0}m}}\end{array}}$

Integramos respecto de x y respecto de t

${\displaystyle {\displaystyle \underset{x_0}{\overset{x}{\int }}\sqrt{\frac{x}{x-x_0}}dx=K{\displaystyle \underset{0}{\overset{t}{\int }}dt}}}$

Para calcular el integrando de la izquierda, se hace al cambio de variable

${\displaystyle \begin{array}{l}{z}^2=\frac{x}{x-x_0}\\ x=x_0\frac{z^2}{z^2-1}dx=-2x_0\frac{z}{{\left(z^2-1\right)}^2}dz\end{array}}$

Tenemos que resolver la integral en z

${\displaystyle -2x_0{\displaystyle \int \frac{z^2}{{\left(z^2-1\right)}^2}dz}}$

Hacemos la descomposición en fracciones

${\displaystyle \begin{array}{l}\frac{z^2}{{\left(z^2-1\right)}^2}=\frac{A}{z-1}+\frac{B}{{\left(z-1\right)}^2}+\frac{C}{z+1}+\frac{D}{{\left(z+1\right)}^2}\\ A=\frac{1}{4}B=\frac{1}{4}C=-\frac{1}{4}D=\frac{1}{4}\end{array}}$

Las integrales ahora, son inmediatas

${\displaystyle \begin{array}{l}-\frac{x_0}{2}{\displaystyle \int \left\{\frac{1}{z-1}+\frac{1}{{\left(z-1\right)}^2}-\frac{1}{z+1}+\frac{1}{{\left(z+1\right)}^2}\right\}dz=}\\ -\frac{x_0}{2}\left\{\ln \left(z-1\right)-\frac{1}{z-1}-\ln \left(z+1\right)-\frac{1}{z+1}\right\}=-\frac{x_0}{2}\left\{\ln \frac{z-1}{z+1}-\frac{2z}{z^2-1}\right\}\end{array}}$

Deshacemos el cambio de variable

${\displaystyle -\frac{x_0}{2}\left\{\ln \frac{\sqrt{x}-\sqrt{x-x_0}}{\sqrt{x}+\sqrt{x-x_0}}-\frac{2\sqrt{x(x-x_0)}}{x_0}\right\}=\frac{x_0}{2}\ln \frac{\sqrt{x}+\sqrt{x-x_0}}{\sqrt{x}-\sqrt{x-x_0}}+\sqrt{x(x-x_0)}}$

Teniendo en cuenta la definición de tanh^-1(x)

${\displaystyle {\tanh }^{-1}(x)=\frac{1}{2}\ln \frac{1+x}{1-x}}$

El integrando lo expresamos en una forma más compacta

${\displaystyle x_0{\tanh }^{-1}\left(\sqrt{\frac{x-x_0}{x}}\right)+\sqrt{x(x-x_0)}}$

Finalmente, el resultado de la integral definida

${\displaystyle \begin{array}{l}{\displaystyle \underset{x_0}{\overset{x}{\int }}\sqrt{\frac{x}{x-x_0}}dx=K{\displaystyle \underset{0}{\overset{t}{\int }}dt}}\\ x_0{\tanh }^{-1}\left(\sqrt{\frac{x-x_0}{x}}\right)+\sqrt{x(x-x_0)}=Kt\end{array}}$

Como vemos, el valor del integrando para el límite inferior x₀ es cero

Representamos esta función implícita para t entre 0 y 5 con K=1 y x₀=1

>> syms x t;
>> x0=1;
>> K=1;
>> ezplot(x0*atanh(sqrt((x-x0)./x))+sqrt(x.*(x-x0))-K*t,[0,5])
>> grid on

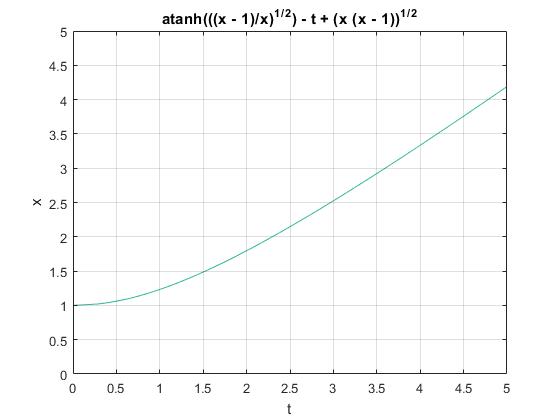
Alternativamente, utilizamos fplot, para representar t en función de x desde x=x₀ a x=5 y luego, hacemos un intercambio de ejes con el comando view

x0=1;
K=1;
f=@(x) (x0*atanh(sqrt((x-x0)./x))+sqrt(x.*(x-x0)))/K;
fplot(f,[x0,5]);
xlabel('x')
ylabel('t')
grid on
xlim([0,5])
view(90,-90)

Concepto de campo

Supongamos, que solamente está presente la carga Q, después de haber retirado la carga q del punto P. Se dice que la carga Q crea un campo eléctrico en el punto P. Al volver a poner la carga q en el punto P, cabe imaginar que la fuerza sobre esta carga la ejerce el campo eléctrico creado por la carga Q.

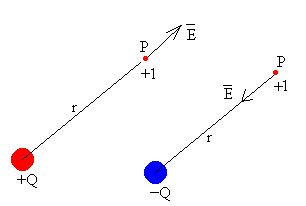
Cada punto P del espacio que rodea a la carga Q tiene una nueva propiedad, que se denomina campo eléctrico $\overrightarrow{E}$ que describiremos mediante una magnitud vectorial, que se define como la fuerza sobre la unidad de carga positiva imaginariamente situada en el punto P.

${\displaystyle \overrightarrow{E}=\frac{1}{4\pi {\epsilon }_0}\frac{Q}{r^2}\widehat{r}}$

La unidad de medida del campo en el S.I. de Unidades es el N/C

En la figura, hemos dibujado el campo en el punto P producido por una carga Q positiva y negativa, respectivamente.

Concepto de potencial

Del mismo modo que hemos definido el campo eléctrico, el potencial es una propiedad del punto P del espacio que rodea la carga Q. Definimos potencial V como la energía potencial de la unidad de carga positiva imaginariamente situada en P, V=E_p/q. El potencial es una magnitud escalar.

${\displaystyle V=\frac{1}{4\pi {\epsilon }_0}\frac{Q}{r}}$

La unidad de medida del potencial en el S.I. de unidades es el volt (V).

Relaciones

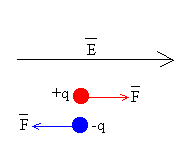
Una carga en el seno de un campo eléctrico $\overrightarrow{E}$ experimenta una fuerza proporcional al campo cuyo módulo es F=qE, cuya dirección es la misma, pero el sentido puede ser el mismo o el contrario dependiendo de que la carga sea positiva o negativa.

El campo eléctrico es conservativo

Un fuerza es conservativa cuando el trabajo de dicha fuerza es igual a la diferencia entre los valores inicial y final de una función que solo depende de las coordenadas. A dicha función se le denomina energía potencial.

${\displaystyle \underset{A}{\overset{B}{{\displaystyle \int }}}\overrightarrow{F}·\overrightarrow{dl}=E_{pA}-E_{pB}{E}_p=E_p(x,y,z)}$

El trabajo de una fuerza conservativa a lo largo de un camino cerrado es cero.

${\displaystyle {{\displaystyle \oint }}^{\text{}}\overrightarrow{F}·\overrightarrow{dl}=0}$

De igual modo tendremos que

${\displaystyle \underset{A}{\overset{B}{{\displaystyle \int }}}\overrightarrow{E}·\overrightarrow{dl}=V_A-V_B}$

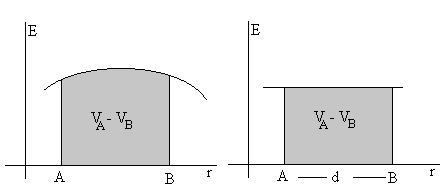
En la figura, vemos la interpretación geométrica. La diferencia de potencial es el área bajo la curva entre las posiciones A y B. Cuando el campo es constante

V_A-V_B=E·d que es el área del rectángulo sombreado.

El campo eléctrico es conservativo lo que quiere decir que en un camino cerrado se cumple

${\displaystyle {{\displaystyle \oint }}^{\text{}}\overrightarrow{E}·\overrightarrow{dl}=0}$

Dado el potencial V calculamos el vector campo eléctrico $\overrightarrow{E}$ , mediante el operador gradiente.

${\displaystyle \overrightarrow{E}=-\overrightarrow{\nabla }V=-\frac{\partial V}{\partial x}\widehat{i}-\frac{\partial V}{\partial y}\widehat{j}-\frac{\partial V}{\partial z}\widehat{k}}$

En el capítulo campos dependientes del tiempo, veremos que se produce un campo eléctrico no conservativo E_i cuando el flujo del campo mágnético a través de un circuito de área S, cambia con el tiempo

${\displaystyle \begin{array}{l}{V}_{\epsilon }=-\frac{d\Phi }{dt}\\ {\displaystyle \oint \overrightarrow{E_i}·\overrightarrow{dl}}=-\frac{d}{dt}{\displaystyle \underset{S}{\int }\overrightarrow{B}·\overrightarrow{dS}}\end{array}}$

Referencias

Para el apartado, Movimiento de una parícula cargada

Roberto De Luca, Marco Di Mauro, Orazio Faella, Adele Naddeo. Interacting charges and the classical electron radius. Eur. J. Phys. 39 (2018) 025706