Fluidoak

Fluidoen dinamika

Depositu bat hustu (I)

Depositu bat hustu (II)

Urak bultzatutako
kohetea

Oszilazioak, U
itxurako hodi batean

Oszilazioak, ontzi
komunikatuetan

 Fluido errealak.
Poiseuille-ren legea

Gas baten
biskositatea

Likido baten
biskositatea

Fluido bat bi zilindro
ardazkideren tartean

Ontzi bat kapilar
batetik deskargatzen

Kapilardun ontzi baten
karga eta deskarga

Desintegrazio-kate
baten analogia

Erregimen laminarra
eta zurrunbilotsua

Magnus efektua

Poiseuille-ren legea

Stokes-en formula

Saiakuntza

Biskositatea (likatasuna)

Biskositatea, edo likatasuna, fluidoaren geruzen arteko barne-marruskadura da. Biskositatearen eraginez, fluido baten geruza bati beste baten gainean irristarazteko indarra eragin behar zaio.

Ondoko irudiak fluido bat adierazten du, bi xaflen artean zapalduta, azpiko xafla finkoa dda eta gainekoa mugikorra.

Xafla mugikorra ukitzen ari den fluido-geruzak xafla horren abiadura bera dauka, eta aldiz, azpiko xaflarekin kontaktuan dagoen fluido-geruza geldi dago. Bitarteko geruza guztien abiadurak handituz doaz azpitik gorantz, irudiko bektoreek adierazten duten bezala. Horrelako fluxu bati laminar deritzo (geruzatakoa).

Higidura horren ondorioz, likido-zati batek aldiune batean ABCD forma dauka, baina, denbora apur bat igaro ondoren, deformatu egingo da eta ABC'D' forma atzemango du.

Demagun fluido horren bi geruza, biak S sekziodunak, baina bata x posizioan eta bestea x+dx. Bien arteko abiadura-diferentziari dei diezaiogun dv.

Aplikatu behar den azalera unitateko indarra, abiadura-gradientearen proportzionala da. Izan ere, proportzionaltasun-konstanteari biskositate deritzo, h.              (1)

Abiaduraren aldakuntza uniformea bada (deribatua konstantea) irudikoa bezala, orduan (1) adierazpena honela berridatz daiteke:

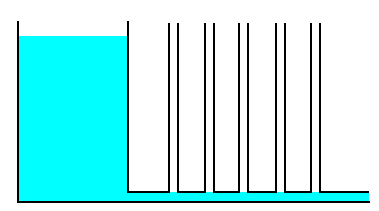
Ondorengo irudian, depositu handi batek ur-maila konstantea dauka, azpiko zulotik ura irteten da eta hodi horizontalean zehar desplazatzen da. Horretaz gain, hodi horizontalak zenbait hodi manometriko bertikal dauzka presioa markatzeko:  p=p₀+r gh. Hodi horizontala itxita dagoenean (likidoa geldi) hodi manometrikoek altuera bera markatzen dute denek, baina likidoa mugitzen denean, ordea, manometroek presio-distribuzio ezberdina markatzen dute fluido motaren arabera. Irudiak bi adibide erakusten ditu:

• Fluido ideala

Fluido idealak (ezkerrekoak) ez dauka biskositaterik, deposituko zulotik irteten da, Torricelli-ren teoremaren arabera, abiadurarekin, bere energia potentzial guztia (h altuerari dagokiona) energia zinetiko bilakatzen delako. Ondoren, Bernoulli-ren ekuazioa aplikatuz, erraz froga daiteke manometro guztietan likidoaren altuera nulua izan behar dela.

• Fluido likatsua

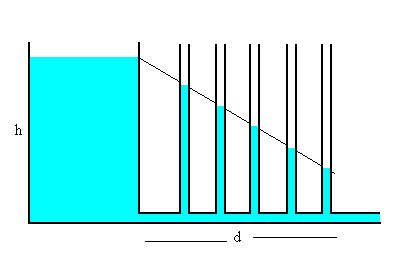Fluido likatsuan, ordea, (eskumako irudia) energiaren balantzea ezberdina da. Deposituko zuloa irekitzean, irteerako abiadura idealarena baino txikiagoa da. Manometroek altuera beherakorrak markatzen dituzte, biskositate-bidezko marruskadurak daudela erakutsiz. Fluidoaren elementuek daukaten energia potentzialaren zati bat bero bilakatu da, eta fluidoa mugitu ahala gero eta gehiago galtzen da. Horregatik markatzen dute manometroek gero eta altuera gutxiago.

Zenbait likidoren biskositatea:

Poiseuille-ren legea

Demagun fluido likatsu bat hodi batetik zirkulatzen ari dena, hodiaren bi muturren arteko presio-diferentziaren eraginez (hodiaren luzera eta erradioa, L eta R).

F=(p₁−p₂)p r²

Indar hori ordezkatzen bada (1) formulan, baina kontutan izan A azalera, kasu honetan, zilindroaren horma dela, alegia 2pRL.

Minus zeinua ipini dugu v gutxitu egiten delako r-rekiko.

• Abiaduren profila

Goiko ekuazio hori integratuz abiaduren profila lortzen da, hau da, likidoaren v abiadura r distantziaren menpe, alegia, zilindroaren ardatzeraino dagoen distantziaren menpe. Kontutan izan, horma ukitzen ari den fluidoak (r=R) abiadura nulua duela.

Ekuazio hori parabola bat da.

Hortaz, fluxu likatsuak profil parabolikoa dauka, eta abiadura maximoa zilindroaren zentroan gertatzen da (fluido idealetan, berriz,  profila laua da).

• Emaria edo kaudala

Emaria edo kaudala deitzen zaio, hodiaren sekzio bat denbora unitatean zeharkatzen duen fluidoaren bolumenari.

Fluxu likatsuak simetria zilindrikoa duenez, har ditzagun eraztun formako gainazal elementuak. Eraztunak r erradioa dauka eta dr lodiera. Denbora unitate batean eraztun hori zeharkatzen duen fluido kantitatea hau da:  v(2p rdr). Fluidoaren v abiadura hodiaren ardatzetik r distantziara, bider 2prdr, eraztunaren perimetroaren azalera.

Eta emari totala lortzen da, eraztun ezberdinen emariak gehituz, integratuz:

Ikusten denez, emaria, G, biskositatearen alderantziz proportzionala da (h), hodiaren erradioarena ber lau eta presio-gradientearena, alegia (p₁-p₂)/L-rena, zuzenki proportzionala.

Fluidoaren batezbesteko abiadura kalkulatzen badugu, <v>, orduan emaria honela adieraz daiteke, G=πR²<v> eta beraz, presio-diferentzia honela:

Stokes-en formula

Objektu bat fluido batean barrena desplazatzen ari denean fluidoak egiten dion erresistentziak menpekotasuna du objektuaren abiadura erlatiboarekin eta objektuaren formarekin. Fluxu erregimena laminarra bada (eta hala izaten da, abiadura neurri batetik pasatzen ez bada) marruskadura-indarra sortzen dute ia soilik fluidoaren geruzek, objektuaren gainazaletik abiatuta, bata bestearen gainean irristatzen dutelako. Esperimentalki egiaztatu da, horrelako marruskadura-indarra abiadura erlatiboaren lehen berreduraren proportzionala dela. Esfera baten kasurako, indar horren adierazpenari Stokes-en formula deritzo:

R esferaren erradioa, v abiadura eta h fluidoaren biskositatea.

Stokes-en formula esperimentalki aplika daiteke, esaterako, fluido baten biskositatea neurtzeko.

Saiakuntza

Fluido erreal bat (likatsua) hodi zilindriko batean zirkulatzen simulatuko da.

Aukeran idatz daitezke:

• Presio-gradientea, 1, 2 edo 3, zerrenda tolesgarriko hiruetatik bat aukeratuz (1 txikia, 2 ertaina eta 3 handia).
• Fluidoaren Biskositatea, 1, 2 edo 3, zerrenda tolesgarriko hiruetatik bat aukeratuz (1 txikia, 2 ertaina eta 3 handia).

Hasi botoian klik egin.

Fluidoko zenbait partikularen abiadura erakusten da, hodiaren ardatzetik zenbait distantzia ezberdinetara, abiaduren profila osoaren itxura behatzeko. Ikus daitekeenez, partikulen abiadurak presio-gradientearekiko zuzenki proportzionalak dira, (p₁-p₂)/L, baina h biskositatearen alderantziz proportzionalak.