Para un gas ideal monoatómico la energía de las moléculas es solamente cinética E=mv²/2. En la expresión deducida en las páginas anteriores

${\displaystyle dn=\frac{2N}{\sqrt{\pi }{\left(kT\right)}^{3/2}}{E}^{1/2}\exp \left(\frac{-E}{kT}\right)dE}$

efectuamos el cambio de variable E por v.

${\displaystyle E=\frac{1}{2}m{v}^2\frac{dn}{dv}=mv\frac{dn}{dE}}$

Resultando la expresión

${\displaystyle dn=N{\left(\frac{m}{2\pi kT}\right)}^{3/2}\exp \left(-\frac{m{v}^2}{2kT}\right)4\pi v^{2}dv}$

que es la fórmula de Maxwell para la distribución de velocidades de las moléculas de un gas ideal. Nos proporciona el número dn de moléculas que se mueven con una velocidad comprendida entre v y v+dv independientemente de la dirección del movimiento.

Utilizando el valor de la integral

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^2\exp (-\alpha x^2)dx}=\frac{1}{4}\sqrt{\frac{\pi }{{\alpha }^3}}}$

>> syms x;
>> syms a positive
>> int('x^2*exp(-a*x^2)',x,0,inf)
ans =pi^(1/2)/(4*a^(3/2))

Integramos la fórmula de Maxwell entre 0 e ∞ y obtenemos el número N de partículas

Velocidad media y velocidad cuadrática media

Como hemos deducido al principio de esta página, el número dn de moléculas que se mueven con una velocidad comprendida entre v y v+dv independientemente de la dirección del movimiento es

${\displaystyle dn=N{\left(\frac{m}{2\pi kT}\right)}^{3/2}\exp \left(-\frac{m{v}^2}{2kT}\right)4\pi v^{2}dv}$

Teniendo en cuenta los valores de las integrales

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^3\exp (-\alpha x^2)dx}=\frac{1}{2{\alpha }^2}\\ {\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^4\exp (-\alpha x^2)dx}=\frac{3}{8}\sqrt{\frac{\pi }{{\alpha }^5}}\end{array}}$

>> syms x;
>> syms a positive
>> int('x^3*exp(-a*x^2)',x,0,inf)
ans =1/(2*a^2)

>> int('x^4*exp(-a*x^2)',x,0,inf)
ans =(3*pi^(1/2))/(8*a^(5/2))

Hallamos la velocidad media y de la velocidad cuadrática media.

1. La velocidad media

${\displaystyle <v>=\frac{1}{N}{\displaystyle \underset{0}{\overset{\infty }{\int }}vdn}=\sqrt{\frac{8kT}{\pi m}}}$

2. La velocidad cuadrática media

${\displaystyle \begin{array}{l}<v^2>=\frac{1}{N}{\displaystyle \underset{0}{\overset{\infty }{\int }}{v}^{2}dn}=\frac{2}{m}<E>=\frac{3kT}{m}\\ \frac{1}{2}m<v^2>=\frac{3}{2}kT\end{array}}$

es la energía media de las moléculas.

La raíz cuadrada del valor medio del cuadrado de las velocidades se denomina v_rms

${\displaystyle v_{rms}=\sqrt{<v^2>}=\sqrt{\frac{3kT}{m}}}$

3. La velocidad para la cual la función de distribución presenta un máximo.

${\displaystyle \frac{d}{dv}\left(\frac{dn}{dv}\right)=0v_{máx}=\sqrt{\frac{2kT}{m}}}$

>> syms a x;
>> y=x^2*exp(-a*x^2);  %a=m/(2kT)
>> solve(diff(y))
ans =          0
 -1/a^(1/2)
  1/a^(1/2)

Ejemplos

Constante de Boltzmann k=1.3805·10^-23 J/K

Número de Avogadro N_A=6.0225·10²³ /mol

Calcular la v_rms del oxígeno a 500 K

${\displaystyle v_{rms}=\sqrt{\frac{3·1.3805·{10}^{-23}·500}{0.032/6.0225·{10}^{23}}}=624.3\text{m/s}}$

Representamos la función de distribución de velocidades moleculares del oxígeno a la temperatura de 1000 K.

${\displaystyle \frac{1}{N}\frac{dn}{dv}=4\pi {\left(\frac{m}{2\pi kT}\right)}^{3/2}\exp \left(-\frac{m{v}^2}{2kT}\right)v^2}$

Las líneas verticales indican

• la velocidad del máximo de la distribución, v_máx
• la velocidad media, <v>
• La velocidad, v_rms

%Hidrógeno (H2), Oxígeno (O2), Nitrógeno (N2), Helio (He), 
Neón (Ne), Argón (Ar)
masa=[2, 32, 28, 4, 10, 18];
T=1000; %temperatura
indice=2; %Oxígeno

cociente=(0.001*masa(indice))/(1.3805*6.0225*2*T); 
f= @(x) 4*pi*(cociente/pi)^(3/2)*exp(-cociente*x.^2).*x.^2;
fplot(f,[0,3000])
Vp=sqrt(1.0/cociente);
Vrms=sqrt(3.0/cociente/2);
Vmedia=sqrt(8*Vp^2/(2*pi));
line([Vp,Vp],[0,1.2e-3],'lineStyle','--')
line([Vrms,Vrms],[0,1.2e-3],'lineStyle','--','color','r')
line([Vmedia,Vmedia],[0,1.2e-3],'lineStyle','--','color','b')
grid on
xlabel('v(m/s)')
ylabel('dn/dv')
title('Velocidades de las moléculas de un gas ideal')
fprintf('Velocidad máxima: %3.1f, media: %3.1f, rms: %3.1f\n',Vp,Vmedia,Vrms);

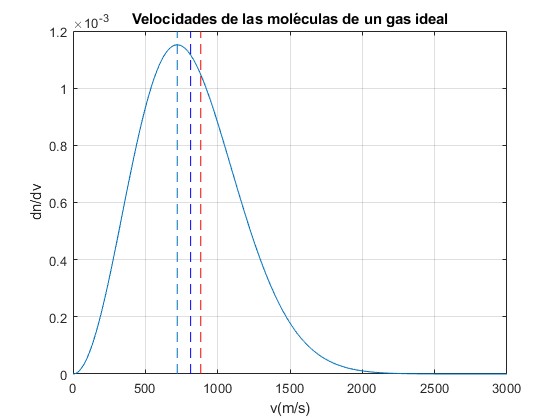
Velocidad máxima: 720.9, media: 813.4, rms: 882.9

El lector interesado puede modificar este script para

• Comparar la distribución de las velocidades de un gas ideal a distintas temperaturas
• Comparar la distribución de las velocidades de varios gases ideales a la misma temperatura.

Fórmula general

Existe otra forma más general de deducir la distribución de velocidades de Maxwell

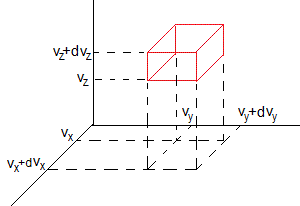
El número de moléculas cuya velocidad está comprendida entre $\overrightarrow{v}$ y $\overrightarrow{v}+\overrightarrow{dv}$ es decir, entre v_x y v_x+dv_x, v_y y v_y+dv_y, v_z y v_z+dv_z, de acuerdo a la ley de Boltzmann es

${\displaystyle dn=c·\exp \left(-\frac{m{v}^2}{2kT}\right)d{v}_x·d{v}_y·d{v}_z}$

donde c es una constante a determinar sabiendo que el número total de moléculas es N. Se efectúa una integral triple entre los límites -∞ y +∞,

${\displaystyle \begin{array}{l}dn=c·\exp \left(-\frac{m{v}^2}{2kT}\right)d{v}_x·d{v}_y·d{v}_z\hfill \\ \begin{array}{l}N={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}c·\exp \left(-\frac{m{v}^2}{2kT}\right)d{v}_x·d{v}_y·d{v}_z}}}=\\ c·{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-\frac{m{v}_x^2}{2kT}\right)}d{v}_x·{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-\frac{m{v}_y^2}{2kT}\right)}d{v}_y·{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-\frac{m{v}_z^2}{2kT}\right)}d{v}_z=\\ c\sqrt{\frac{2\pi kT}{m}}\sqrt{\frac{2\pi kT}{m}}\sqrt{\frac{2\pi kT}{m}}=c{\left(\frac{2\pi kT}{m}\right)}^{3/2}\end{array}\hfill \end{array}}$

Teniendo en cuenta el resultado de la integral

${\displaystyle {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp (-\alpha x^2)dx}=\sqrt{\frac{\pi }{\alpha }}}$

>> syms x;
>> syms a positive;
>> int('exp(-a*x^2)',x,-inf,inf)
ans =pi^(1/2)/a^(1/2)

se obtiene

${\displaystyle dn=N{\left(\frac{m}{2\pi kT}\right)}^{3/2}·\exp \left(-\frac{m{v}^2}{2kT}\right)d{v}_x·d{v}_y·d{v}_z}$

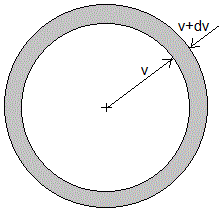
Calculamos el número de moléculas cuyo módulo de la velocidad está comprendida entre v y v+dv, independientemente de la dirección

El diferencial de volumen, es el de una capa esférica de radio v y espesor dv tal como se muestra en la figura

${\displaystyle dn=N{\left(\frac{m}{2\pi kT}\right)}^{3/2}·\exp \left(-\frac{m{v}^2}{2kT}\right)4\pi v^{2}dv}$

que es la misma expresión que hemos obtenido al principio de la página

Coordenadas polares

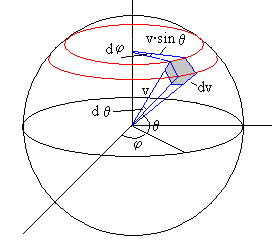
Expresamos el elemento de volumen dv_x·dv_y·dv_z en coordenadas polares. Para ello,

• Trazamos dos esferas concéntricas de radio v y v+dv.

• Cortamos las esferas por dos planos meridianos que pasan por los ángulos φ y φ+dφ.

• Finalmente, cortamos las esferas por dos planos paralelos de ángulos θ y θ+dθ

El volumen comprendido es paralepípedo elemental de color gris de la figura tiene por lados

dv, v·sinθ·dφ, v·dθ

Su volumen es

v²·sinθ·dv·dθ·dφ

El número de moléculas cuyo módulo de la velocidad esta comprendido entre v y v+dv y cuya dirección está comprendida entre φ y φ+dφ, θ y θ+dθ, es

${\displaystyle dn=N{\left(\frac{m}{2\pi kT}\right)}^{3/2}\exp \left(-\frac{m{v}^2}{2kT}\right)v^2·\sin \theta ·dv·d\theta ·d\phi }$

Estudiamos dos aplicaciones de la forma general de la distribución de velocidades de Maxwell son

Sublimación de un sólido

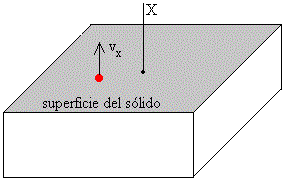
Utilizamos la fórmula en coordenadas rectangulares, para calcular el número de moléculas cuya componente X de la velocidad está comprendida entre v_x, v_x+dv_x independientemente de los valores de las otras dos componentes, integrando respecto de v_y y v_z entre los límites -∞ y +∞ .

${\displaystyle \begin{array}{l}d{n}_x=N{\left(\frac{m}{2\pi kT}\right)}^{3/2}\left\{{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-\frac{m{v}_y^2}{2kT}\right)}d{v}_y·{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\exp \left(-\frac{m{v}_z^2}{2kT}\right)}d{v}_z\right\}\exp \left(-\frac{m{v}_x^2}{2kT}\right)d{v}_x=\\ N{\left(\frac{m}{2\pi kT}\right)}^{1/2}\exp \left(-\frac{m{v}_x^2}{2kT}\right)d{v}_x\end{array}}$

La sublimación de un sólido se explica de la siguiente forma: a una temperatura T saldrán de la superficie del cristal aquellos átomos cuya componente X de la velocidad sea positiva y mayor que un valor mínimo v_min, tal que

${\displaystyle \frac{1}{2}m{v}_{x,\min }^2=\phi }$

donde φ es la energía de evaporación de las moléculas en la superficie del cristal

${\displaystyle n_x=N{\left(\frac{m}{2\pi kT}\right)}^{1/2}·{\displaystyle \underset{v_{\min }}{\overset{\infty }{\int }}\exp \left(-\frac{m{v}_x^2}{2kT}\right)d{v}_x}}$

En general, el número de moléculas que tienen una componente X de su velocidad mayor que un valor mínimo se obtiene

${\displaystyle \begin{array}{l}{n}_x=\frac{1}{2}N\left(1-\text{erf}(x)\right)x=\sqrt{\frac{m}{2kT}}{v}_x\\ \text{erf}(x)=\frac{2}{\sqrt{\pi }}{\displaystyle \underset{0}{\overset{x}{\int }}\exp (-z^2)dz}\end{array}}$

erf(x) se denomina función error.

>> syms x vm;
>> syms a positive; %a=m/(2kT)
>> sqrt(a/pi)*int('exp(-a*x^2)',x,vm,inf)
ans =1/2 - erf(a^(1/2)*vm)/2

El efecto termoiónico es un fenómeno análogo a la sublimación de las moléculas en un sólido, aunque los electrones obedecen a la estadística cuántica de Fermi-Dirac.

Evaporación de la atmósfera

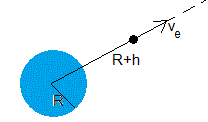
Se denomina velocidad de escape v_e de una partícula que está a una distancia r del centro de la Tierra, a la velocidad que hemos de proporcionarle para que llegue al infinito con velocidad nula

${\displaystyle \frac{1}{2}m{v}_e^2-\frac{GmM}{R+h}=\mathrm{0,}{v}_e=\sqrt{\frac{2GM}{R+h}}}$

La velocidad de escape de una partícula situada a h=500 km de altura sobre la superficie de la Tierra es v_e=10 776 m/s. Los datos son: masa de la Tierra, M=5.98·10²⁴ kg, radio de la Tierra R=6.37·10⁶ m, constante G=6.67·10^-11 Nm²/kg²

Para cualquier temperatura T siempre hay algunas moléculas cuya velocidad es mayor que la de escape. Una molécula situada en la parte inferior de la atmósfera no podrá escapar al espacio exterior incluso cuando su velocidad sea mayor que la de escape, debido a que colisiona con otras moléculas perdiendo parte de su energía.

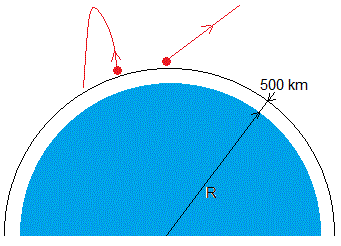
Sin embargo, las moléculas situadas en la parte superior de la atmósfera (exósfera), donde la densidad es muy pequeña, su probabilidad de colisión con otras moléculas es muchísimo menor. Aquellas moléculas cuya velocidad es superior a la de escape se pierden en el espacio exterior. A esta situación se la conoce como evaporación atmosférica.

En la figura, se muestra la Tierra y la exósfera que comienza a partir de una altura aproximada de h=500 km y dos moléculas una lenta que regresa atraída por la Tierra y otra rápida que se pierde en el espacio.

La exósfera es la última capa de la atmósfera cuya densidad tiende a cero y se funde con el espacio exterior. La mayor parte de las órbitas de los satélites artificiales están en esta última capa

La temperatura de la exósfera es de alrededor de T=1000 K. La velocidad rms de las moléculas es

${\displaystyle \begin{array}{l}\frac{1}{2}m\langle v^2\rangle =\frac{3}{2}kT\\ v_{rms}=\sqrt{\langle v^2\rangle }=\sqrt{\frac{3kT}{m}}\end{array}}$

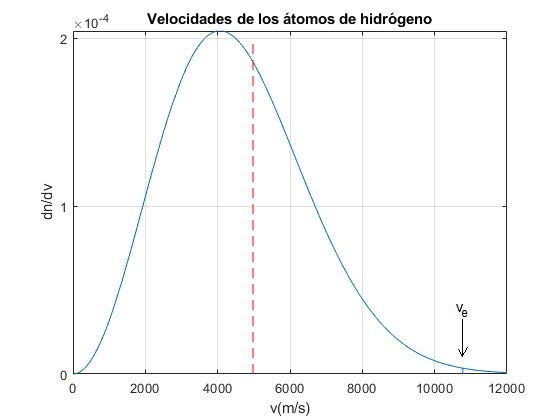
Para los átomos de hidrógeno, v_rms=5 000 m/s, que es inferior a la velocidad de escape. Los datos son: masa de un protón, m=1.67·10^-27 kg, constante k=1.38·10^-23 J/K

Representamos la distibución de velocidades de los átomos de hidrógeno a la temperatura T= 1000 K. Se señala la velocidad v_rms y la velocidad de escape v_e

m=1.6725e-27; %átomo de hidrógeno
k=1.3805e-23;
T=1000; %temperatura
h=500e3; %altura exósfera
f= @(v) 4*pi*(m/(2*pi*k*T))^(3/2)*exp(-m*v.^2/(2*k*T)).*v.^2;
fplot(f,[0,12000])
Vrms=sqrt(3*k*T/m);
Ve=sqrt(2*6.67e-11*5.98e24/(6.37e6+h)); %velocidad de escape
disp([Vrms;Ve])
line([Vrms,Vrms],[0,2e-4],'lineStyle','--','color','r')
line([Ve,Ve],[0,f(Ve)])
grid on
xlabel('v(m/s)')
ylabel('dn/dv')
title('Velocidades de los átomos de hidrógeno')

Como hemos demostrado, el número de moléculas cuyo módulo de la velocidad esta comprendido entre v y v+dv y cuya dirección está comprendida entre φ y φ+dφ, θ y θ+dθ, es

${\displaystyle dn=N{\left(\frac{m}{2\pi kT}\right)}^{3/2}\exp \left(-\frac{m{v}^2}{2kT}\right)v^2·\sin \theta ·dv·d\theta ·d\phi }$

Flujo

Se define el flujo Φ, como el número de moléculas que atraviesan la sección A por unidad de área y unidad de tiempo.

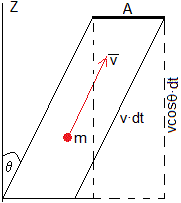
Calculamos primero, el número de moléculas con velocidad v que atraviesan el área A en el tiempo dt, que se mueven en una dirección que hace un ángulo θ con la normal a sección, son las contenidas en el volumen cilíndrico de base A y altura v·cosθ·dt. Se multiplica el número de moléculas por unidad de volumen (dn/V) por el volumen del cilindro de la figura.

(dn/V)·A·v·cosθ·dt.

El número de moléculas con velocidad v que atraviesan la sección A por unidad de área y unidad de tiempo es

(dn/V)·v·cosθ

Para calcular la integral triple, establecemos los límites de integración para las variables v, φ y θ.

• Los límites de la primera integral respecto de φ, son 0 y 2π, se integra para todos los ángulos
• Se integra para ángulos θ comprendidos entre 0 y π/2, ya que cuando θ>π/2, v·cosθ se hace negativa y la partícula se aleja de la sección, no la atraviesa.
• Se integra para las velocidades, desde v_e a ∞.

El flujo es

${\displaystyle \begin{array}{l}\Phi =\frac{1}{V}{\displaystyle \int v·\cos \theta ·dn=}\\ \frac{1}{V}{\displaystyle \underset{v_e}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}N{\left(\frac{m}{2\pi kT}\right)}^{3/2}\exp \left(-\frac{m{v}^2}{2kT}\right)}}}(v·\cos \theta )·v^2\sin \theta ·dv·d\theta ·d\phi =\\ 2\pi \frac{N}{V}{\left(\frac{m}{2\pi kT}\right)}^{3/2}{\displaystyle \underset{v_e}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\exp \left(-\frac{m{v}^2}{2kT}\right)v^3}}\cos \theta ·\sin \theta dv·d\theta =\\ \frac{N}{V}\pi {\left(\frac{m}{2\pi kT}\right)}^{3/2}{\displaystyle \underset{v_e}{\overset{\infty }{\int }}\exp \left(-\frac{m{v}^2}{2kT}\right)v^{3}dv}\end{array}}$

Se ha utilizado el resultado de la integral

${\displaystyle {\displaystyle \underset{0}{\overset{\pi /2}{\int }}\cos \theta ·\sin \theta ·d\theta =\frac{1}{2}}}$

Para obtener el flujo, integramos por partes

${\displaystyle \begin{array}{l}{\displaystyle \int \exp \left(-\frac{m{v}^2}{2kT}\right)v^{3}dv,}\{\begin{array}{l}x=v^2,dx=2v·dv\\ dy=\exp \left(-\frac{m{v}^2}{2kT}\right)vdv,y=-\frac{kT}{m}\exp \left(-\frac{m{v}^2}{2kT}\right)\end{array}\\ =-v^2\frac{kT}{m}\exp \left(-\frac{m{v}^2}{2kT}\right)+2\frac{kT}{m}{\displaystyle \int \exp \left(-\frac{m{v}^2}{2kT}\right)vdv}=\\ -v^2\frac{kT}{m}\exp \left(-\frac{m{v}^2}{2kT}\right)-\frac{kT}{m}\frac{2kT}{m}\exp \left(-\frac{m{v}^2}{2kT}\right)=-\frac{kT}{m}\left\{v^2+\frac{2kT}{m}\right\}\exp \left(-\frac{m{v}^2}{2kT}\right)\end{array}}$

Evaluamos el integrando entre los límites v_e e ∞. El resultado es

${\displaystyle \begin{array}{l}\Phi =\frac{N}{V}\pi {\left(\frac{m}{2\pi kT}\right)}^{3/2}\frac{kT}{m}\left\{v_e^2+\frac{2kT}{m}\right\}\exp \left(-\frac{m{v}_e^2}{2kT}\right)\\ =\frac{1}{2}\frac{N}{V}\sqrt{\frac{m}{2\pi kT}}\left\{v_e^2+\frac{2kT}{m}\right\}\exp \left(-\frac{m{v}_e^2}{2kT}\right)\end{array}}$

El numéro de atomos de hidrógeno que se evaporan (se pierden en el espacio exterior) en la unidad de tiempo es

${\displaystyle 4\pi {\left(R+h\right)}^2\Phi }$

Sabiendo que el número de átomos de hidrógeno por unidad de volumen a la altura h=500 km es N/V=10¹¹ m^-3 calculamos el flujo Φ y el número de átomos de hidrógeno que se evaporan en la unidad de tiempo

m=1.6725e-27; %átomo de hidrógeno
k=1.3805e-23;
T=1000; %temperatura
h=500e3; %altura exósfera
Ve=sqrt(2*6.67e-11*5.98e24/(6.37e6+h)); %velocidad de escape
F=1e11*sqrt(m/(2*pi*k*T))*(Ve^2+2*k*T/m)*exp(-m*Ve^2/(2*k*T))/2;
disp(F)
disp(F*4*pi*(6.37e6+h)^2)

  8.1164e+11
  4.8138e+26

Referencias

WoPhO Problems and Solutions. 2013, Physics Cup. Atmospheric Evaporation by Jeans Escape