El gas ideal bidimensional está encerrado en un recipiente que dispone de un émbolo móvil, de modo que se puede aumentar o disminuir el volumen (área) del gas. Las moléculas se colocan inicialmente en posiciones aleatorias, las direcciones de sus velocidades también son aleatorias y sus magnitudes son iguales y proporcionales a la raíz cuadrada de la temperatura. Tenemos de este modo un sistema de partículas en equilibrio a la temperatura T, que chocan elásticamente entre sí y con las paredes del recipiente.

El programa calcula el cambio de momento lineal que experimentan las moléculas al chocar con el émbolo y divide este cambio entre el tiempo. El cociente es una medida de la fuerza que ejerce el émbolo sobre las moléculas del gas, o también se puede interpretar como una medida de la presión del gas.

Veremos que partiendo de una distribución inicial en el que las velocidades de las moléculas son iguales en módulo, al cabo de un cierto tiempo unas moléculas tienen mayor velocidad y otras moléculas tienen menor velocidad. La distribución de velocidades cuando se alcanza el equilibrio sigue la ley de distribución de Maxwell.

Cuando nos referimos a las velocidades de las moléculas, las medimos respecto del centro de masas del sistema gaseoso, por tanto, la presión y la temperatura del gas no se modifican si el recipiente que lo contiene está en movimiento.

Si suponemos que las velocidades en el sentido positivo del eje X (o del eje Y o Z) son igualmente probables que en el sentido negativo, las velocidades medias a lo largo de los ejes son cero, es decir.

<v_x>=<v_y>=<v_z>=0.

Por otra parte, se cumplirá que las velocidades a lo largo del eje X no estarán relacionadas con las velocidades a lo largo del eje Y o Z, por tanto,

${\displaystyle <v_x^2>=<v_y^2>=<v_z^2>}$

Como el cuadrado del módulo de la velocidad es $v^2=v_x^2+v_y^2+v_z^2$ resulta que $<v^2>=3<v_x^2>$

La presión ejercida por el gas

Supongamos que el gas está encerrado en un recipiente, tal como se muestra en la figura. El recipiente dispone de un émbolo móvil de área A. Para mantener fijo el émbolo es necesario ejercer una fuerza F, normalmente a la superficie del émbolo. El valor de la fuerza F es igual al producto de la presión ejercida por el gas por el área del émbolo.

F=PA

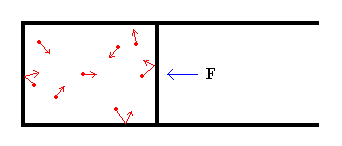
Las moléculas del gas chocan elásticamente con el émbolo, de modo que la componente X de la velocidad cambia de sentido. Por tanto, el cambio en el momento lineal de cada molécula es

Δp=2mv_x

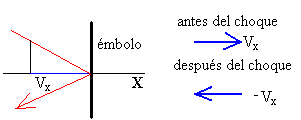
Si el número total de moléculas que chocan con el émbolo en el intervalo de tiempo comprendido entret y t+Δt es N_x, la variación de momento lineal será 2mv_xN_x.

Calculamos N_x considerando que solamente la mitad de las moléculas, en promedio, tienen el sentido de la velocidad hacia la parte positiva del eje X, es decir, se dirigen hacia el émbolo.

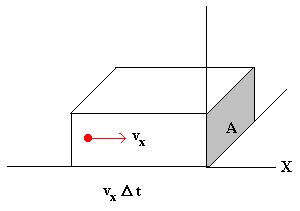
Si suponemos que las moléculas que chocan con el émbolo tienen el mismo valor de la componente X de la velocidad, cruzarán el área A en el tiempo Δt todas las partículas contenidas en el volumen Av_xΔt. Si n es el número de partículas por unidad de volumen N_x valdrá entonces, nAv_xΔt/2.

La variación de momento lineal Δp en el intervalo de tiempo comprendido entre t y t+Δt es mv_x nAv_xΔt.

La fuerza sobre el émbolo es el cociente entre el cambio de momento lineal y el tiempo que tarda en efectuarse dicho cambio.

${\displaystyle F=\frac{\Delta p}{\Delta t}=\frac{m{v}_{x}nA{v}_x\Delta t}{\Delta t}=nA(m{v}_x^2)}$

y por tanto, la presión ejercida por el gas vale

${\displaystyle P=n(m{v}_x^2)}$

Todas las moléculas no tienen el mismo valor v_x de la velocidad, sino que la distribución de velocidades es tal que su valor medio cuadrático es $<v_x^2>$ Por tanto, en la expresión de la presión P, hemos de sustituir $v_x^2$ por $<v_x^2>$ .

${\displaystyle P=nm<v_x^2>=\frac{2}{3}n\langle \frac{1}{2}m{v}^2\rangle }$

ya que $<v_x^2>=\frac{1}{3}<v^2>$

El último término que aparece en la fórmula, es el valor medio de la energía cinética.

Definición cinética de la temperatura

La ecuación de estado de un gas ideal relaciona las propiedades macroscópicas, presión P, el volumen V y temperatura T.

PV=μRT

Siendo μ el número de moles.

El número n de moléculas por unidad de volumen se obtiene dividiendo el número total de moléculas N entre el volumen del recipiente V.

${\displaystyle n=\frac{N}{V}=\frac{\mu N_0}{V}}$

donde N₀ el número de Avogadro

Introduciendo n en la expresión de la presión del gas, obtenemos

${\displaystyle P=\frac{2}{3}\frac{N}{V}\langle \frac{1}{2}m{v}^2\rangle =\frac{2}{3}\frac{\mu N_0}{V}\langle \frac{1}{2}m{v}^2\rangle }$

Comparando esta ecuación con la de estado de un gas ideal, se llega a la definición cinética de temperatura

${\displaystyle \langle \frac{1}{2}m{v}^2\rangle =\frac{3}{2}\frac{R}{N_0}T}$

El cociente entre las dos constantes R y N₀ es otra constante que designamos por k, la constante de Boltzmann.

${\displaystyle k=\frac{8.314\text{ J/(K·mol)}}{\text{6}{\text{.022 10}}^{\text{23}}\text{/mol}}=1.380{\text{ 10}}^{\text{-23}}\text{J/K}}$

La temperatura absoluta definida, por ejemplo, para un termómetro de gas ideal es una medida directa de la energía media de traslación de las moléculas del gas.

${\displaystyle \frac{3}{2}kT=\langle \frac{1}{2}m{v}^2\rangle }$

La temperatura podría medirse en unidades de energía, el hecho de que se mida en grados se debe a la definición tradicional de temperatura, que se estableció antes de que se descubriese la relación antes mencionada.

Otra forma útil de la ecuación de los gases perfectos es

P·V=N·k·T

Donde N es el número de moléculas contenidas en el recipiente de volumen V.

Como las moléculas de un gas ideal solamente tienen energía cinética, se desprecia la energía potencial de interacción. La energía interna U de un gas ideal es N veces la energía cinética media de una molécula.

${\displaystyle U=N\langle \frac{1}{2}m{v}^2\rangle =\frac{3}{2}NkT=\frac{3}{2}\mu RT}$

Actividades

Se introduce

• La temperatura del modelo de gas ideal bidimensional, en el control titulado Temperatura.
• El "volumen" del recipiente, en el control titulado Posición émbolo.
• El número de partículas, en el control de edición titulado N. partículas

Se pulsa el botón titulado Nuevo

Relacionar la presión y el "volumen" del gas manteniendo constante la temperatura. ¿Se mantiene constante el producto P por V?

Relacionar la presión y la temperatura manteniendo fijo el volumen (la posición del émbolo). ¿Aumenta linealmente la presión con la temperatura?