Medida de la constante de Boltzmann

Partículas suspendidas en agua

Si un conjunto de partículas cada una de volumen V y densidad ρ_s está suspendida en un líquido de densidad ρ_l. En el equilibrio, el número de partículas por unidad de volumen cambiará con la altura x de la forma

$n (x) = n_{0} \exp (- \frac{(ρ_{s} - ρ_{l}) V g}{k T} x)$

n₀ es la concentración de partículas en el fondo del recipiente, n(x) es la concentración a una altura x por encima del fondo, T es la temperatura absoluta, y k es la constante de Boltzmann.

La deducción de esta fórmula es idéntica a la de la variación de la presión con la altura en una atmósfera isoterma.

Einstein en 1905, sugirió que esta distribución exponencial se podría observar con partículas idénticas de muy pequeño tamaño y que a partir de la medida de la variación de la densidad n(x), se podría determinar la constante k. Jean Perrin realizó por primera vez este experimento en 1908.

En el experimento descrito en el artículo citado en las referencias, se emplean esferas de poliestireno de 1.011 µm de diámetro y de densidad ρ_s=1.053 g/cm³

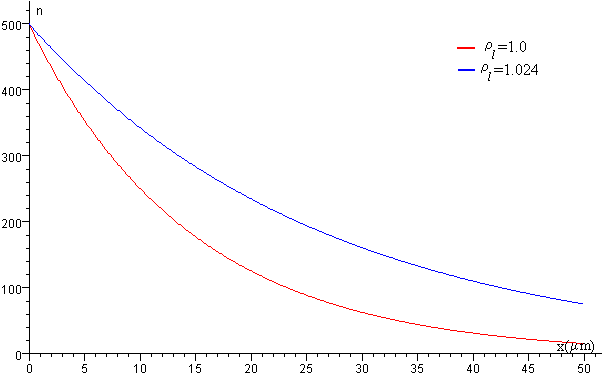
Las esferas se suspenden en agua pura ρ_l=1.0 g/cm³o en una solución de agua y glicerol cuya densidad es ligeramente superior a la del agua, y cuyo efecto es la de expandir la distribución exponencial tal como se muestra en la figura.

Actividades

El programa interactivo genera un número aleatorio próximo a la unidad que representa la densidad del líquido ρ_l en g/cm³ en el que se suspenden las partículas
La densidad de las esferas se ha fijado en ρ_s=1.053 g/cm³
El diámetro 2r de las esferas se ha fijado en 1.011·10^-6 m, el volumen de una esfera de radio r es V=4πr³/3
La temperatura ambiente se ha fijado en T=295 K

Se pulsa el botón titulado Nuevo.

Se representa la distribución de partículas (puntos de color rojo) con la altura x medida en µm=10^-6 m

Actuamos sobre la la barra de desplazamiento Zona, para contar el número de partículas en los intervalos especificados.

Los intervalos aparecen ampliados en la parte derecha, simulando que se observan con el microscopio.

Contamos el número de partículas que hay en el intervalo 0-5 µm y se lo asignamos a la altura x=2.5 µm, (en el primer control de edición de la parte izquierda del applet)

Actuamos en la flecha derecha de la barra de desplazamiento titulado Zona

Contamos el número de partículas que hay en el intervalo 5-10 µm y se lo asignamos a la altura x=7.5 µm

Continuamos el proceso hasta completar 10 intervalos.

Para evitar el proceso tedioso de contar las partículas, el programa interactivo lo hace por nosotros, y nos proporciona este dato.

x(μm)	2.5	7.5	12.5	17.5	22.5	27.5	32.5	37.5	42.5	47.5
n	540	391	297	210	154	114	82	66	40	21

Se representa

En el eje horizontal, la altura x en µm
En el eje vertical, el logaritmo neperiano del número de partículas, ln(n)

Se representan los datos “experimentales” y la recta que mejor ajusta. Determinamos la constante de Boltzmann k a partir de la pendiente de la recta.

x=2.5+(0:9)*5;
y=[540,391,297,210,154,114,82,66,40,21];
plot(x,log(y),'ro','markersize',4,'markerfacecolor','r')
xlabel('x(\mum)')
ylabel('log(n)')
title('Constante de Boltzmann')
grid on

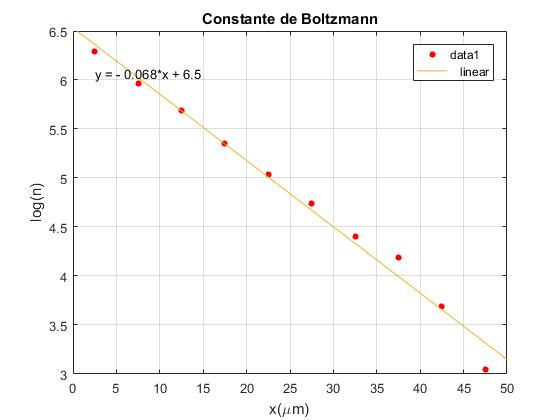
En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p1 y p2 del polinomio (recta) y=p1*x+p2 de ajuste.

$\ln (n) = \ln (n_{0}) - \frac{(ρ_{s} - ρ_{l}) V g}{k T} x$

La densidad del líquido es ρ_l=1.004 g/cm³=1004 kg/m³

La pendiente de la recta en la gráfica es -0.067666. Como el eje horizontal está en µm, la pendiente es -0.067666·10⁶ m^-1

$\frac{(ρ_{s} - ρ_{l}) V g}{k T} \frac{(1053 - 1004) \cdot \frac{4}{3} π {(\frac{1}{2} 1.011 \cdot 10^{- 6})}^{3} \cdot 9.8}{k \cdot 295} = 0.067666 \cdot 10^{6}$

k=1.302·10^-23 J/K

El valor que aparece en las tablas de las constantes es k=1.38·10^-23 J/K

Zona

Evaporación de un líquido volátil

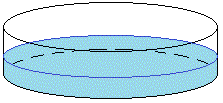
Un recipiente cilíndrico de pequeña altura comparado con el radio de su base, contiene un líquido volátil (alcohol etílico). El recipiente dispone de una tapa que se puede abrir o cerrar.

Cuando se abre, el recipiente disminuye su masa con el tiempo debido a la evaporación
Cuando se cierra, la evaporación sigue produciéndose, pero el número de moléculas que se escapan del líquido será igual (en valor medio) al número de moléculas que se incorporan al mismo, estableciéndose un estado de equilibrio dinámico

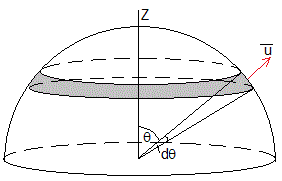
Supondremos que todas las moléculas en la fase vapor tienen la misma velocidad u relativa al líquido en el recipiente e igual a la velocidad media <v> de las moléculas a la temperatura T.

$< v > = \sqrt{\frac{8 k T}{π m}}$

Donde la constante de Boltzmann k=1.3805·10^-23 J/K, m=M/N_A es la masa de una molécula. N_A=6.0225·10²³ mol^-1 es el número de Avogadro y M la masa molar. Para el alcohol etílico M=46.07·10^-3 kg/mol

El número de moléculas dN_θ cuya velocidad u forma un ángulo θ con la dirección vertical Z está dada por

$d N_{θ} = \frac{2 π r^{2} \sin θ \cdot d θ}{2 π r^{2}} N = N \sin θ \cdot d θ$

El numerador es el área de la banda de color gris de la superficie esférica de radio r, comprendida entre θ y θ+dθ. El denominador es el área de media esfera. N es el número total de moléculas en el vapor

El valor medio <u_z> de la componente Z de la velocidad u de estas moléculas vale

$< u_{z} > = \frac{1}{N} \int_{0}^{π / 2} (u \cos θ) N \sin θ \cdot d θ = \frac{u}{2} \int_{0}^{π / 2} \sin (2 θ) \cdot d θ = \frac{u}{2}$

Experiencia

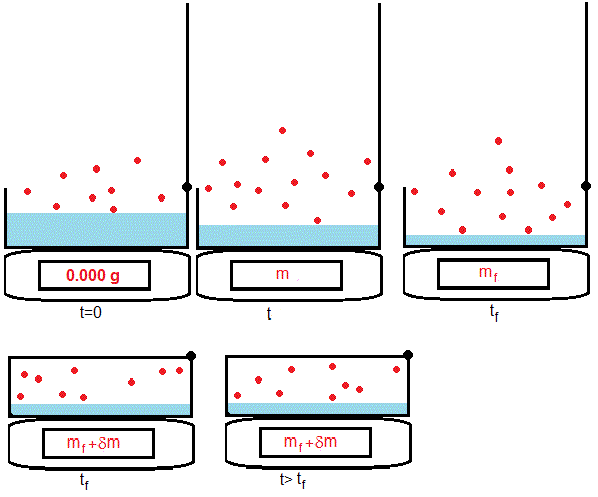
Un recipiente con líquido volátil se coloca sobre una balanza electrónica que aprecia 0.001 g. En el instante inicial t=0, se abre el recipiente y se pone la balanza a cero.

A medida que el líquido se evapora, su masa disminuye, se van tomando n medidas a intervalos regulares de tiempo Δt, por ejemplo cada 30 s o cada 60 s.

Cuando se toma la última medida m_f en el instante t_f=n·Δt, se cierra rápidamente el recipiente para evitar la evaporación del líquido. Se anota la nueva medida que indica la balanza m_f+δm. La diferencia δm entre ambas, es una cantidad muy pequeña.

Como el recipiente está cerrado, a partir de este instante t_f, la balanza seguirá midiendo lo mismo, m_f+δm

Recipiente abierto

Una masa dm de moléculas abandona la superficie del líquido en el intervalo de tiempo comprendido entre t y t+dt con velocidad media <u_z> en la dirección vertical. La razón del cambio de momento lineal con el tiempo es

$| f_{r} | = \frac{d (m < u_{z} >)}{d t} = < u_{z} > \frac{d m}{d t}$

donde |f_r| es la fuerza de reacción de las moléculas que se evaporan

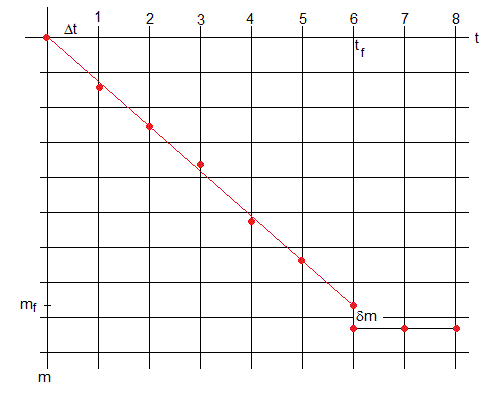
Las medidas en la etapa de evaporación se ajustan a una línea recta de pendiente dm/dt. Conocida |f_r| y dm/dt, se despeja la componente Z de la velocidad media de las moléculas <u_z> tal como se indica a continuación

Recipiente cerrado

Cuando se cierra rápidamente el recipiente, la medida de la masa en la balanza es un poco menor δm que corresponde a la fuerza de reacción |f_r| de las moléculas que chocan con la tapa.

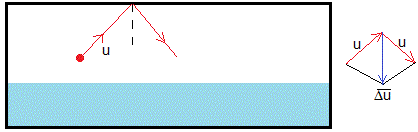
Las moléculas cuando chocan con la tapa, cambian la dirección de su velocidad. El cambio de velocidad $\vec{Δ u}$ es la diferencia entre los dos vectores (velocidad final menos inicial) y tiene dirección vertical y sentido hacia abajo, tal como se indica a la derecha de la figura. La tapa ejerce una fuerza sobre las moléculas en la misma dirección y sentido. Las moléculas ejercen una fuerza |f_r| sobre la tapa del recipiente en sentido contrario (hacia arriba). La masa que mide la balanza es más pequeña δm

$| f_{r} | = δ m \cdot g$

La velocidad media u de las moléculas vale

$\begin{array}{l} δ m \cdot g = < u_{z} > \frac{d m}{d t} \\ u = \frac{2 δ m \cdot g}{\frac{d m}{d t}} \end{array}$

Ejemplo 1

El líquido volátil es alcohol etílico cuya masa molecular es M=46.07 g/mol. La pendiente de la recta y δm, valen respectivamente,

$\begin{array}{l} \frac{d m}{d t} = \frac{0.17}{5 \cdot 30} g/s \\ δ m = 0.01 g \end{array}$

Valores estimados a partir de la gráfica de la figura 3 del segundo artículo citado en las referencias

Obtenemos la velocidad media de las moléculas u=<v>=346 m/s

La velocidad media de las moléculas a la temperatura ambiente de T=290 K es

$< v > = \sqrt{\frac{8 k T}{π m}} = \sqrt{\frac{8 \cdot 1.3805 \cdot 10^{- 23} \cdot 290}{π \frac{46.07 \cdot 10^{- 3}}{6.0225 \cdot 10^{23}}}} = 365 m/s$

Ejemplo 2

Otra posibilidad es calcular el orden de magnitud de la constante de Boltzmann k a partir del dato de la velocidad media de las moléculas u=<v>

El líquido volátil es alcohol etílico. La pendiente de la recta y δm, valen respectivamente,

$\begin{array}{l} \frac{d m}{d t} = 7.74 \cdot 10^{- 4} g/s \\ δ m = 1.3 \cdot 10^{- 2} g \end{array}$

Obtenemos la velocidad media de las moléculas u=<v>=329.2 m/s. Despejamos la constante k sabiendo que la temperatura ambiente es T=298 K

$k = \frac{π < v >^{2} m}{8 T} = \frac{π \cdot 329^{2} \cdot \frac{46.07 \cdot 10^{- 3}}{6.0225 \cdot 10^{23}}}{8 \cdot 298} = 1.09 \cdot 10^{- 23} J/K$

Actividades

El programa interactivo es una animación, de la experiencia que se describe en el tercer artículo mencionado en las referencias (ejemplo 2). Se toman 16 datos de la masa evaporada del líquido volátil cada 60 s, hasta el instante t_f=960 s. En este instante se cierra el recipiente

t(s)	0	60	120	180	240	300	360	420	480	540	600	660
m(g)	0	0.046	0.093	0.139	0.186	0.232	0.279	0.325	0.372	0.418	0.464	0.511
t(s)	720	780	840	900	960
m(g)	0.557	0.604	0.650	0.697	0.743

t=0:60:960;
m=[0, 0.046, 0.093, 0.139, 0.186, 0.232, 0.279, 0.325, 0.372, 0.418, 0.464, 
0.511, 0.557, 0.604, 0.650, 0.697, 0.743];
plot(t,-m,'ro','markersize',3,'markerfacecolor','r')
xlabel('t(s)')
ylabel('m(g)')
title('Evaporación de un líquido')
grid on

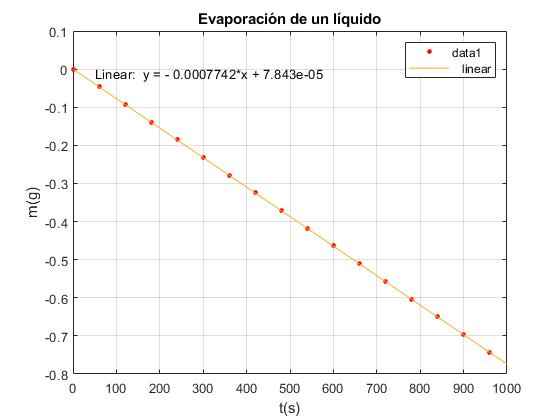
En el menú seleccionamos Tools/Basic Fitting, aparece el cuadro de diálogo TYPES OF FIT donde marcamos la casilla linear

La pendiente de la recta es dm/dt=-7.742·10^-4 g/s

Para la toma de medidas en los instantes, 60, 120, 180, ... s. Utilícese la combinación de botones pausa || y paso a paso >|

Referencias

Horne M., Farago P., Oliver J., An experiment to measure Boltzmann's constant. Am. J. Phys. 41, March 1975, pp. 344-348

Salvatore Ganci. Determination of the mean velocity of a molecule. Am. J. Phys. 71 (3), March 2003. pp. 267-268

Marcela P Escobar, R Antonio Zárate, Francisco A Calderón, Sergio Curilef. Simple experimental determination of the Boltzmann constant using a volatile liquid. Eur. J. Phys. 42 (2021) 065102