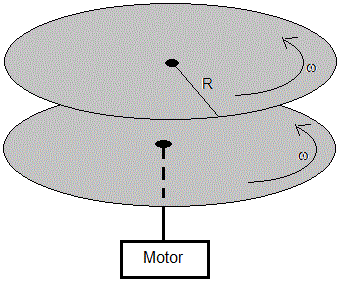
Sean dos placas planas paralelas en forma de disco de radio R. Se conecta la placa inferior a un motor, debido a la viscosidad, al cabo de un cierto tiempo, el aire entre los dos discos y el disco superior adquieren la misma velocidad angular de rotación ω.

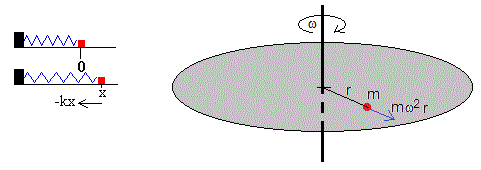
En la página titulada Trabajo, energía cinética y energía potencial, vimos que la fuerza que ejerce un muelle elástico sobre una partícula, F=-kx es conservativa y la energía potencial es kx²/2, tomando como nivel cero de energía potencial cuando el muelle está sin deformar, x=0

Cuando una partícula de masa m está situada a una distancia r del eje de rotación de una plataforma que gira con velocidad angular constante ω, experimenta una fuerza centrífuga mω²r. Esta fuerza es conservativa y su energía potencial es

${\displaystyle U(r)=-\frac{1}{2}m{\omega }^2{r}^2}$

tomando como nivel cero de energía potencial cuando la partícula está en el eje r=0.

En una atmósfera isoterma, el número n de moléculas por unidad de volumen decrece con la altura y. Del mismo modo, en un campo de fuerza centrífugo, el número de moléculas por unidad de volumen n(r) varía con la distancia r al eje de rotación.

Supongamos que entre las placas en rotación a velocidad angular ω constante, hay un gas ideal (aire) formado por moléculas de masa m a la temperatura T

${\displaystyle n(r)=n_0\exp \left(-\frac{U(r)}{kT}\right)=n_0\exp \left(\frac{m{\omega }^2{r}^2}{2kT}\right)}$

Una relación similar se obtiene para la presión p, ya que para un gas ideal a la temperatura T, p=nKT

${\displaystyle p(r)=p_0\exp \left(\frac{m{\omega }^2{r}^2}{2kT}\right)}$

p₀ es la presión en el eje de los discos, r=0. En el exterior y en el borde de los discos r=R, la presión es la atmósférica

${\displaystyle \begin{array}{l}{p}_{atm}=p_0\exp \left(\frac{m{\omega }^2{R}^2}{2kT}\right)\\ p(r)=p_{atm}\exp \left(-\frac{m{\omega }^2{R}^2}{2kT}\left(R^2-r^2\right)\right)\end{array}}$

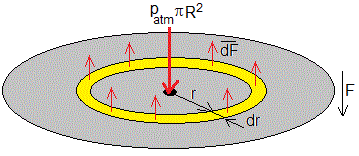
Calculamos la fuerza que ejerce la presión sobre el disco superior

• La presión atmosférica ejerce una fuerza hacia abajo p_atm(πR²)

• La presión del gas en el interior de los discos varía con la distancia al eje r, ejerce una fuerza hacia arriba

La resultante F hacia abajo es

${\displaystyle \begin{array}{l}F=p_{atm}\left(\pi R^2\right)-{\displaystyle \underset{0}{\overset{R}{\int }}p(r)\left(2\pi r·dr\right)=}\\ p_{atm}\left(\pi R^2\right)-2\pi p_{atm}{\displaystyle \underset{0}{\overset{R}{\int }}r·\exp \left(-\frac{m{\omega }^2}{2kT}\left(R^2-r^2\right)\right)dr=}\\ p_{atm}\left(\pi R^2\right)\left\{1-{\left(\frac{v_{máx}}{\omega R}\right)}^2\left(1-\exp \left(-{\left(\frac{\omega R}{v_{máx}}\right)}^2\right)\right)\right\}\end{array}}$

Donde, $v_{máx}=\sqrt{\frac{2kT}{m}}$ es la velocidad de las moléculas del gas para la cual la función de distribución de velocidades presenta un máximo

Habitualmente, ωR<<v_máx, salvo en ultracentrifugadoras. Para el oxígeno v_máx a 300 K es

>> sqrt(2*1.3805e-23*300/(0.032/6.0225e23))
ans =  394.8274

Desarrollamos en serie, exp(x)≈1+x+x²/2

${\displaystyle \begin{array}{l}F\approx p_{atm}\left(\pi R^2\right)\left\{1-{\left(\frac{v_{máx}}{\omega R}\right)}^2\left(1-\left[1+{\left(\frac{\omega R}{v_{máx}}\right)}^2+\frac{1}{2}{\left(\frac{\omega R}{v_{máx}}\right)}^4\right]\right)\right\}\\ F\approx \frac{1}{2}{p}_{atm}\left(\pi R^2\right){\left(\frac{\omega R}{v_{máx}}\right)}^2=\frac{\pi }{4}\rho R^4{\omega }^2\end{array}}$

Donde, la densidad es ρ=nm, y la ecuación del gas ideal es p=nkT

Ejemplo: Sea el radio de los discos R=15.7 cm, la velocidad angular de rotación ω=1800 rpm=60π rad/s, la densidad del aire es ρ=1.2 kg/m³

La fuerza, F=20.3 N

Diferencia de presión en una estación espacial

Una estación espacial tiene forma de cilindro de radio R₀, lleno de aire. El cilindro gira alrededor de su eje de simetría con velocidad angular ω, para proporcionar una aceleración en su superficie lateral similar a la de la gravedad en la superficie de la Tierra. ω²R₀≈g=9.81 m/s²

Si la temperatura T dentro de la estación espacial es constante, calcularemos el cociente entre la presión del aire en el eje del cilindro y en su superficie lateral

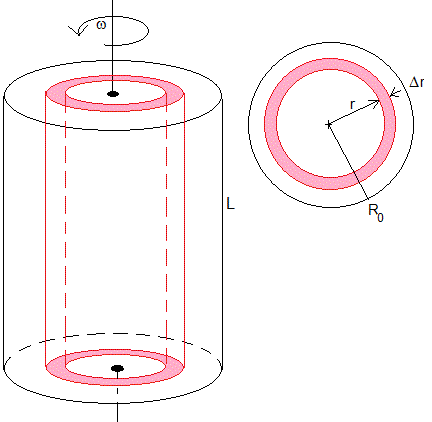
Consideremos una capa cilíndrica de radio r longitud L y espesor Δr. La diferencia de presión entre las dos superficies laterales (interior y exterior), multiplicada por el área de dichas superficies es igual la fuerza centrífuga sobre la porción de masa de aire contenido en dicha capa.

${\displaystyle \left(p(r+\Delta r)-p(r)\right)2\pi rL=\left(\rho 2\pi rL·\Delta r\right){\omega }^{2}r}$

2πrL es la superficie lateral de un cilindro de radio r y longitud L

$\pi {\left(r+\Delta r\right)}^{2}L-\pi r^{2}L\approx 2\pi rL·\Delta r$, es el volumen de la capa cilíndrica y ρ es la densidad del aire.

En el límite cuando Δr→0

${\displaystyle \frac{dp}{dr}=\rho {\omega }^{2}r}$

Si consideramos el aire como un gas ideal

${\displaystyle \begin{array}{l}pV=\frac{m}{M}RT\\ \rho =\frac{M}{RT}p\end{array}}$

m es la masa de aire, M=28.9 g/mol es su peso molecular y R=8.3143 J/(K·mol) la constante de los gases

${\displaystyle \frac{dp}{dr}=\frac{M{\omega }^2}{RT}pr}$

Integrando

${\displaystyle \begin{array}{l}{\displaystyle \underset{p(0)}{\overset{p(R)}{\int }}\frac{dp}{p}}=\frac{M{\omega }^2}{RT}{\displaystyle \underset{0}{\overset{R_0}{\int }}rdr}\\ \ln \left(\frac{p(R)}{p(0)}\right)=\frac{M{\omega }^2}{2RT}{R}_0^2\\ \frac{p(0)}{p(R)}=\exp \left(-\frac{Mg{\omega }^2}{2RT}{R}_0^2\right)\end{array}}$

La presión en el eje p(0) es menor que la presión en la superficie cilíndrica p(R)

Medida de la diferencia de presión

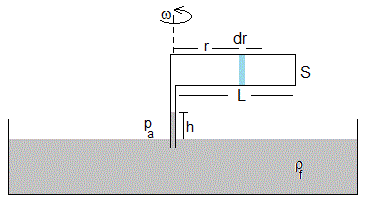
Sea un tubo horizontal de sección S y longitud L cerrado por un extremo que contiene aire de densidad ρ_a a la temperatura constante T. Por el otro extremo, termina en un tubo delgado que está sumergido en un depósito de líquido de densidad ρ_f.

El depósito es grande y está abierto a la atmósfera cuya presión es p_a.

El tubo horizontal gira con velocidad angular constante ω, alrededor de un eje, que coincide con el del tubo vertical.

Supondremos que el aire del depósito es un gas ideal a una temperatura constante T. Ignoramos el volumen y los efectos de la capilaridad del tubo vertical de pequeño radio

A una disminución de la presión en el eje, le corresponde una ascensión h del líquido del depósito por el tubo vertical. Vamos a realcionar la velocidad angular de rotación ω y la altura h a la que asciende el líquido

Partimos de la ecuación, que nos relaciona el gradiente de presión dp/dr con la distancia r al eje de rotación

${\displaystyle \frac{dp}{dr}=\rho {\omega }^{2}r}$

Supondremos que el aire es una gas ideal, la presión p y la densidad ρ son proporcionales

${\displaystyle \begin{array}{l}pV=\frac{m}{M}RT,\rho =\frac{m}{V}=\frac{pM}{RT}\\ \frac{d\rho }{dr}=\frac{M{\omega }^2}{RT}\rho r\end{array}}$

Separando variables e integrando

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{r}{\int }}\frac{d\rho }{\rho }}=\frac{M{\omega }^2}{RT}{\displaystyle \underset{0}{\overset{r}{\int }}r·dr}\\ \ln \left(\frac{\rho }{{\rho }_0}\right)=\frac{M{\omega }^2}{2RT}{r}^2\\ \rho ={\rho }_0\exp \left(\alpha r^2\right),\alpha =\frac{M{\omega }^2}{2RT}\end{array}}$

donde ρ₀ es la densidad del aire para r=0, en el eje de rotación.

La masa de aire de densidad constante ρ_a que contiene el depósito en reposo, es la misma que girando, con una densidad no uniforme que varía con r. De modo que

${\displaystyle {\rho }_{a}SL={\displaystyle \underset{0}{\overset{L}{\int }}{\rho }_0}\exp \left(\alpha r^2\right)(S·dr)}$

dm=(ρS·dr) es la masa contenida en el elemento diferencial de volumen S·dr dibujado en la figura.

Para pequeños valores de la velocidad angular de rotación, ω, aproximamos la exponencial por los dos primeros términos de su desarrollo en serie y a continuación, 1/(1+x)≈1-x, para x<<1

>> syms a x;
>> taylor(exp(a*x^2))
ans =(a^2*x^4)/2 + a*x^2 + 1

Por ejemplo, para el aire a 20 grados: masa molecular M=28.96 kg/mol, la constante R=8.3143 J/(K·mol), T=293 K. El parámetro, α=0.00593ω²

${\displaystyle \begin{array}{l}{\rho }_{a}SL\approx {\displaystyle \underset{0}{\overset{L}{\int }}{\rho }_0}\left(1+\alpha r^2+\mathrm{...}\right)(S·dr)\\ {\rho }_a\approx {\rho }_0\left(1+\frac{1}{3}\alpha L^2\right)\\ {\rho }_0\approx {\rho }_a\left(1-\frac{1}{3}\alpha L^2\right)\\ p_0\approx p_a\left(1-\frac{1}{3}\alpha L^2\right)\end{array}}$

Donde p₀ es la presión en el eje, un poco menor que la presión atmósférica, como consecuencia el líquido del depósito asciende hasta una altura h.

${\displaystyle \begin{array}{l}{p}_a=p_0+{\rho }_{f}gh\\ h=\frac{M{p}_a}{RT}\frac{{\omega }^2{L}^2}{6g{\rho }_f}=\frac{{\omega }^2{L}^2}{6g}\frac{{\rho }_a}{{\rho }_f}\end{array}}$

La altura h es proporcional al cuadrado del producto ωL (la velocidad angular de rotación del tubo horizontal por longitud de dicho tubo)

Referencias

Fred Fisher, R. L. Wild. Demonstration of reduced gas pressure in a centrifugal field. Am. J. Phys. 47(5) may 1979, pp. 450-451

Lim Yung-kuo. Problems and Solutions on Mechanics. World Scientific (1994). Problem 1267, pp. 447-448. Problem 1261, pp. 434-436