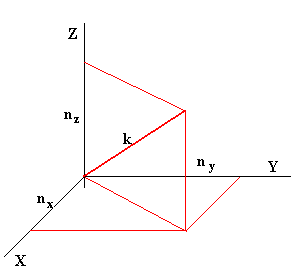
La energía de una partícula de masa m que se mueve en una región unidimensional de anchura a no puede tener cualquier valor. Cuando resolvemos la ecuación de Schrödinger para una partícula que se mueve en cubo de anchura a obtenemos los niveles de energía que puede ocupar dicha partícula.

${\displaystyle E=\frac{\pi {\hslash }^2}{2m{a}^2}{k}^2{k}^2=n_x^2+n_y^2+n_z^2}$

siendo n_x, n_y, y n_z números enteros positivos.

Cuando a es grande, como ocurre para las partículas de un gas encerrado en un recipiente, los niveles de energía están muy juntos. Nuestra tarea ahora es la de calcular el número de niveles de energía comprendidos en el intervalo entre E y E+dE.

Primero, calculamos el número de niveles en el intervalo entre 0 y E, que es igual a la octava parte del volumen de una esfera de radio k, tal como puede verse en la figura, ya que n_x, n_y, y n_z son números enteros positivos.

${\displaystyle N(E)=\frac{1}{8}\left(\frac{4}{3}\pi k^3\right)=\frac{8\pi V}{3h^3}{\left(2m^3\right)}^{1/2}{E}^{3/2}}$

Siendo V el volumen del recipiente V=a³.

Derivando con respecto de E, obtenemos el número de niveles comprendidos entre E y E+dE.

${\displaystyle g(E)=\frac{4\pi V{\left(2m^3\right)}^{1/2}}{h^3}{E}^{1/2}}$

El número de moléculas cuya energía está comprendida entre E y E+dE se obtiene aplicando la ley de Boltzmann.

${\displaystyle \begin{array}{l}\frac{dn}{dE}=NCg(E)\exp \left(-\frac{E}{kT}\right)\\ dn=CN\frac{4\pi V{\left(2m^3\right)}^{1/2}}{h^3}{E}^{1/2}\exp \left(-\frac{E}{kT}\right)dE\end{array}}$

N es el número total de partículas en el recipiente de volumen V y C es una constante de proporcionalidad que se determina a partir de la condición de que todas las partículas tienen una energía comprendida entre cero e infinito.

${\displaystyle N=CN{\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{4\pi V{\left(2m^3\right)}^{1/2}}{h^3}{E}^{1/2}\exp \left(\frac{-E}{kT}\right)dE}}$

Como la energía de las moléculas es solamente cinética

${\displaystyle E=\frac{1}{2}m{v}^2}$

La integral se convierte en

${\displaystyle 1=C\frac{4\pi V{\left(2m^3\right)}^{1/2}}{h^3}\sqrt{\frac{m^3}{2}}{\displaystyle \underset{0}{\overset{\infty }{\int }}{v}^2\exp \left(\frac{-m}{2kT}{v}^2\right)dv}}$

Teniendo en cuenta el resultado de la integral

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^2\exp (-\alpha x^2)dx=}\frac{1}{4}\sqrt{\frac{\pi }{{\alpha }^3}}}$

>> syms x;
>> syms a positive
>> int('x^2*exp(-a*x^2)',x,0,inf)
ans =pi^(1/2)/(4*a^(3/2)) 

El valor de la constante C de proporcionalidad es

${\displaystyle C=\frac{\sqrt{2}{h}^3}{V\sqrt{2m^3}\sqrt{{\left(2\pi kT\right)}^3}}}$

Introduciendo el valor de C en la fórmula anterior, queda finalmente.

${\displaystyle dn=\frac{2N}{\sqrt{\pi }{\left(kT\right)}^{3/2}}{E}^{1/2}\exp \left(\frac{-E}{kT}\right)dE}$

Hacemos el cambio de variable x=E/(kT)

${\displaystyle dn=\frac{2N}{\sqrt{\pi }}{x}^{1/2}{e}^{-x}dx}$

Representamos (1/N)·dn/dx mediante la función ezplot en el intervalo 0 a 4.

>> syms x;
>> y=2*x^(1/2)*exp(-x)/sym('pi')^(1/2);
>> ezplot(y,[0,4])
>> xlabel('x')
>> ylabel('dn/dx')
>> title('Distribución de la energía entre las moléculas')
>> grid on

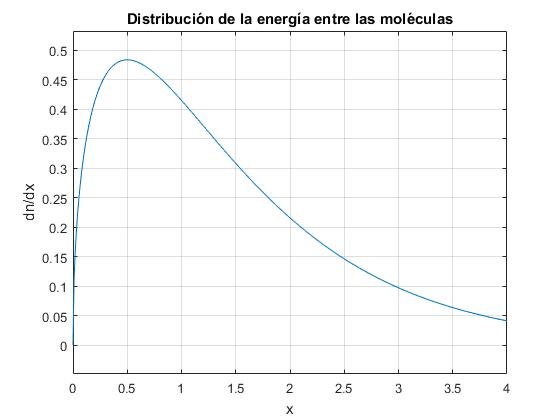
La función de distribución presenta un máximo para x=1/2. Para la energía E=(kT)/2;

>> syms x;
>> y=2*x^(1/2)*exp(-x)/sym('pi')^(1/2);
>> yp=diff(y);
>> solve(yp)
ans =1/2

Número de partículas que tienen una energía menor que E_c

Calculamos el número de partículas que tienen una energía menor que E_c

${\displaystyle N_1=\frac{2N}{\sqrt{\pi }{\left(kT\right)}^{3/2}}{\displaystyle \underset{0}{\overset{E_c}{\int }}{E}^{1/2}\exp \left(\frac{-E}{kT}\right)dE}}$

Llamando x=E/kT

${\displaystyle N_1=\frac{2N}{\sqrt{\pi }}{\displaystyle \underset{0}{\overset{x_c}{\int }}{x}^{1/2}\exp (-x)dx}}$

Calcular la proporción de moléculas de un gas ideal N₁/N a la temperatura T=300 K cuyas energías son menores que E_c=0.06 eV. Datos: 1eV=1.6·10^-19 J, la constante de Boltzmann k=1.38·10^-23 J/K.

${\displaystyle x_c=\frac{E_c}{kT}=\frac{0.06·1.6·{10}^{-19}}{300·1.38·{10}^{-23}}=2.3188}$

>> syms x xc;
>> y=2*x^(1/2)*exp(-x)/sym('pi')^(1/2);
>> p=int(y,0,xc)
p = 1 - (2*xc^(1/2))/(pi^(1/2)*exp(xc)) - erfc(xc^(1/2))
>> subs(p,xc,2.3188)
ans =    0.7997

La proporción de partículas cuya energía es mayor que E_c=0.06 eV es 1-N₁/N=1-0.997=0.2003.

Hacemos el mismo cálculo pero en téminos de la función error, erf. Se hace el cambio de variable y²=x

${\displaystyle N_1=\frac{4N}{\sqrt{\pi }}{\displaystyle \underset{0}{\overset{\sqrt{x_c}}{\int }}{y}^2\exp (-y^2)dy}}$

Se integra por partes

${\displaystyle \begin{array}{l}{N}_1=\frac{4N}{\sqrt{\pi }}{\left(-\frac{1}{2}y\exp (-y^2)+\frac{1}{2}{\displaystyle \int \exp (-y^2)dy}\right)}_0^{\sqrt{x_c}}=\\ \frac{2N}{\sqrt{\pi }}\left(-\sqrt{x_c}\exp (-x_c)+\frac{\sqrt{\pi }}{2}\text{erf}\left(\sqrt{x_c}\right)\right)\end{array}}$

>> syms x xc;
>> int('x^(1/2)*exp(-x)',x,0,xc)
ans =(pi^(1/2)*erf(xc^(1/2)))/2 - xc^(1/2)*exp(-xc)

erf(x) se denomina integral de los errores y viene tabulada en los libros de Matemáticas.

${\displaystyle \text{erf}(x)=\frac{2}{\sqrt{\pi }}{\displaystyle \underset{0}{\overset{x}{\int }}\exp (-y^2)dy}}$

La proporción de partículas cuya energía está comprendida entre 0 y E_c es

${\displaystyle \frac{N_1}{N}=\text{erf}\left(\sqrt{x_c}\right)-\frac{2\sqrt{x_c}}{\sqrt{\pi }}\exp (-x_c)}$

Calculamos la proporción de partículas cuya energía es menor que E_c=0.06 eV a la temperatura T=300 K y obtenemos el mismo resultado

>> xc=0.06*1.6e-19/(1.38e-23*300);
>> p=erf(sqrt(xc))-2*sqrt(xc)*exp(-xc)/sqrt(pi)
p =    0.7997

Los datos experimentales están de acuerdo con la teoría, lo que confirma la aplicabilidad de la estadística de Maxwell-Boltzmann. Por ejemplo, una reacción determinada ocurre solamente si las moléculas tienen cierta energía igual o mayor que E_c. La velocidad de la reacción a una temperatura dada depende entonces, del número de moléculas que tienen una energía mayor o igual que E_c.

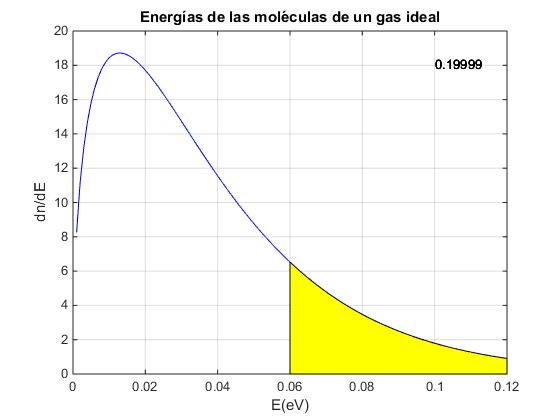
Se representa la función dn/dE y se calcula la proporción de moléculas cuya energía es superior a una dada, es decir, el cociente entre el área sombreada y el área total bajo la curva.

T=300; %temperatura
Ec=0.06; %energía en eV
xc=Ec*11604.49/T;
%proporción de partículas con E>Ec
pr=1-2*(sqrt(pi)*erf(sqrt(xc))/2-sqrt(xc)*exp(-xc))/sqrt(pi);

f=@(x) 2*sqrt(x).*exp(-11604.49*x/T)*1250083.9/(sqrt(pi)*T^(3/2));
E=(0.1:0.1:12)/100;
y=f(E);
hold on
plot(E,y, 'b')
xx=[Ec Ec E(E>Ec & E<0.12) 0.12 0.12];
yy=[0 f(Ec) y(E>Ec & E<0.12) f(0.12) 0];
fill(xx,yy,'y'); %rellena un área de color especificado
text(0.1,18,num2str(pr));
hold off
grid on
xlabel('E(eV)')
ylabel('dn/dE')
title('Energías de las moléculas de un gas ideal')

Energía interna

Hallamos la energía del gas ideal mediante

${\displaystyle \begin{array}{l}U={\displaystyle \underset{0}{\overset{\infty }{\int }}Edn}={\displaystyle \underset{0}{\overset{\infty }{\int }}\frac{2N}{\sqrt{\pi }{\left(kT\right)}^{3/2}}{E}^{3/2}\exp \left(\frac{-E}{kT}\right)dE}=\\ \frac{N}{\sqrt{\pi }{\left(kT\right)}^{3/2}}\frac{m^{5/2}}{\sqrt{2}}{\displaystyle \underset{0}{\overset{\infty }{\int }}{v}^4\exp \left(-\frac{m}{2kT}{v}^2\right)}dv\end{array}}$

Teniendo en cuenta el resultado de la integral

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^4\exp (-\alpha x^2)dx=}\frac{3}{8}\sqrt{\frac{\pi }{{\alpha }^5}}}$

>> syms x;
>> syms a positive
>> int('x^4*exp(-a*x^2)',x,0,inf)
ans =(3*pi^(1/2))/(8*a^(5/2))

Legamos a la expresión

${\displaystyle U=\frac{3}{2}NkT}$

Dividiendo entre N, número de moléculas, obtenemos la energía media de las moléculas es 3kT/2

Por tanto, la energía de las moléculas de un gas ideal monoatómico es proporcional a la temperatura absoluta del gas. Históricamente esta ecuación fue introducida en el siglo XIX mucho antes del desarrollo de la Mecánica Estadística, en conexión con la teoría cinética de los gases.

El número N de moléculas es igual al número de moles μ por el número de Avogadro N₀=6.0225 10²³ mol^-1. El producto del número de Avogadro por la constante de Boltzmann k=1.38 10^-23 J/K nos da la constante R=8.3143 J/(K mol) de los gases ideales.

${\displaystyle U=\frac{3}{2}\mu RT}$