Función de distribución de Boltzmann (II)
Consideremos un sistema aislado compuesto por un gran número de partículas, en el cual, cada partícula puede ocupar alguno de los niveles de energía E0, E1, E2, .... Estos pueden estar cuantizados (como los estados rotacionales o vibracionales de una molécula) o bien, pueden formar un espectro continuo (como la energía cinética de las moléculas de un gas). Por ejemplo, en el modelo de sólido de Einstein, los átomos se representan por osciladores armónicos unidimensionales. Los osciladores interaccionan muy débilmente de modo que la energía de la interacción se puede considerar despreciable frente a la energía del oscilador.
En un momento dado, las partículas están distribuidas entre los diferentes niveles de modo que n0 tienen energía E0, n1 partículas tienen energía E1 y así, sucesivamente.
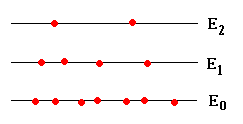
El número total de partículas es:
N=n0+n1+n2+...
y por ser el sistema aislado, la energía total permanece constante.
U=n0E0+n1E1+n2E2+...
Debido a las interacciones y a las colisiones entre las moléculas, los números n0, n1, n2,... están cambiando continuamente. Se puede suponer, que para cada estado macroscópico del sistema, hay una distribución de partículas entre los diversos niveles que es más probable que cualquier otra. Una vez alcanzada esta distribución se dice que el sistema está en equilibrio.
Los números n0, n1, n2, ... pueden entonces fluctuar alrededor de los valores correspondientes a la situación de equilibrio sin que se produzcan efectos macroscópicos.
Vamos a determinar el modo en que las partículas de un sistema aislado se distribuyen entre los niveles de energía permitidos.
Macroestado y microestados
En la estadística clásica las partículas de un sistema son idénticas pero indistinguibles. Esto quiere decir, que a escala macroscópica no podemos distinguir una partícula de otra, pero podemos imaginar que a escala microscópica disponemos de algún procedimiento para identificar las partículas individuales.
Es importante saber diferenciar entre macroestado y microestado. Las propiedades macroscópicas como la presión, y la temperatura está determinadas por el macroestado del sistema. Los microestados correspondientes al mismo macroestado son indistinguibles experimentalmente unos de otros.
Vamos a ayudarnos de dos programas interactivos para comprender los conceptos de macroestado y microestado y para determinar el número de microestados correspondientes a un macroestado dado.
El primer programa es demostrativo y se puede tomar como punto de partida para el segundo que es más interactivo.
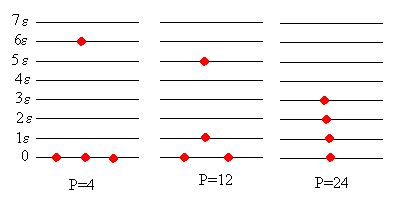
Vamos a examinar los macroestados de un sistema de N=4 partículas con una energía total U=6 unidades.
En el primer macroestado, k=1, tenemos 3 partículas en el nivel fundamental de energía (0) y una partícula en el nivel (6) de energía. La energía total es, por tanto, U=3·0+1·6=6. Pulsando el botón titulado ►, se nos va mostrando los cuatro microestados que corresponden al macroestado dado. Estas son las permutaciones del conjunto de números {0,0,0,6}, que se muestran en la parte derecha.
Pulsamos el botón titulado >>, se nos muestra el segundo macroestado, k=2, en el que tenemos dos partículas en el nivel fundamental (0), una partícula en el nivel (1), y una partícula en el nivel (5). La energía total es, por tanto, U=2·0+1·1+1·5=6. Pulsando el botón titulado ► se nos muestra los 12 microestados correspondiente al macroestado dado. Estas son las permutaciones de {0,0,1,5}, que se muestran en la parte derecha.
Pulsando varias veces el botón >>, llegamos al macroestado que tiene el mayor número de microestados, k=6. La primera partícula está en el nivel fundamental (0), la segunda en el nivel (1), la tercera en el nivel (2), la cuarta en el nivel (3). La energía total es U=1·0+1·1+1·2+1·3=6. El número de microestados son las permutaciones del conjunto de números {0,1,2,3}, que se muestran en la parte derecha.
El segundo programa interactivo es similar al anterior pero además le permite al usuario definir el sistema. Por tanto, consta de dos partes:
- Definición del sistema.
Primero, se elige el número de partículas del sistema, 3, 4 ó 5 en el control de selección desplegable y se pulsa el botón titulado Nuevo.
- Se define el macroestado del sistema
Se arrastra con el ratón el círculo de color negro situada en la parte derecha a alguna de las 50 posiciones posibles marcadas por puntos de color rojo. No se pueden poner dos partículas en la misma posición, pero si en el mismo nivel. No se pueden poner todas las partículas en el mismo nivel.
Cuando se han colocado todas las partículas en los niveles de energía accesibles, se pulsa el botón titulado ►. El programa calcula y muestra todos los microestados correspondientes a un macroestado de energía U dado.
Arrastre con el puntero del ratón el círculo de color negro hacia un punto de color rojo
La distribución más probable
Como se puede comprobar en los dos programas interactivos, el número de microestados Ω correspondientes a un macoroestado k dado por n0 partículas en el nivel E0, n1 partículas en el nivel E1, n2 en el nivel E2, ...viene dado por la fórmula
Donde N es el número total de partículas
Ejemplo.
Si tenemos 3 partículas en el nivel fundamental de energía (0) y una partícula en el nivel (6) de energía. El número de micorestados Ω es
Si tenemos dos partículas en el nivel fundamental (0), una partícula en el nivel (1), y una partícula en el nivel (5).
El postulado fundamental de la mecánica estadística afirma que un sistema en equilibrio tiene la misma probabilidad de estar en cualquiera de sus microestados permitidos. Así, el macroestado que tenga el máximo número de microestados es el macroestado más probable. La distribución {n0, n1, n2, n3...} para la cual Ω tenga el valor más grande es la distribución más probable de las partículas del sistema entre los niveles de energía accesibles al mismo.
Ejemplo:
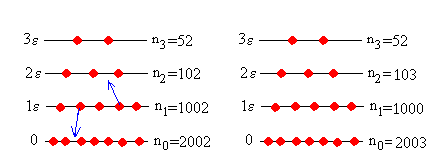
Consideremos la distribución de partículas que se muestra en la figura, en la que hay 2002 en el nivel fundamental, 1002 en el primer nivel, 102 en el segundo, 52 en el tercero y así sucesivamente. El número de microestados de este macroestado particular es
Supongamos que dos partículas del primer nivel (1) interaccionan. Después de la interacción la primera partícula pierde una unidad de energía y va al estado fundamental (0) y la segunda gana una unidad de energía y va al segundo nivel (2).
La energía total del sistema no cambia, ya que la energía de las partículas antes y después de la interacción es la misma (dos unidades). Sin embargo, el número de microestados correspondiente al nuevo macroestado cambia notablemente.
El cociente
Como vemos, pequeños cambios en la distribución del macroestado inicial dan lugar a grandes variaciones en Ω, lo que indican que el sistema está lejos del equilibrio. El sistema estará cerca del equilibrio, cuando un pequeño cambio en la distribución del macroestado inicial no cambia apreciablemente el valor de Ω.
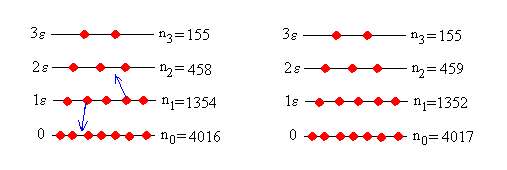
En el ejemplo de la figura, si se produce una interacción entre dos partículas del primer nivel de modo que una gana una unidad de energía y la otra la pierde, es fácil mostrar que el cociente
El número de microestados apenas cambia. Tal es el caso de un sistema en equilibrio térmico en el que las interacciones entre las partículas (choques) cambia el sistema hacia un macroestado que tiene prácticamente el mismo número de microestados que el inicial.
Función de distribución de Boltzmann
Para hallar la distribución más probable del sistema aislado, se precisa calcular el máximo de Ω de modo que el número N de partículas y la energía total U permanezcan constantes. Se trata, pues, de un problema matemático de extremos condicionados.
En otras palabras, tenemos que hallar el máximo de la función Ω(n1,n2,...) o mejor, de su logaritmo neperiano, bajo las condiciones complementarias
Aplicamos el método de los multiplicadores de Lagrange y formamos la nueva función
donde α y β son factores indeterminados. En el sistema de ecuaciones
que junto a las dos condiciones complementarias determinan los dos parámetros α y β y los números, n1, n2, ... del extremo de la función ln(Ω)
Utilizamos la aproximación de Stirling, cuando x es grande, lnx!≈xlnx-x
Con las dos condiciones complementarias calculamos los factores α y β
Por los que los números ni de ocupación del nivel de energía Ei son
Esta es la función de distribución de Boltzmann, el denominador se denomina función de partición Z. El otro parámetro β se determina sabiendo que la energía total del sistema es U.
El valor del extremo de lnΩ vale
el parámetro β=1/kT, k se denomina constante de Boltzmann y T la temperatura absoluta. La función de distribución de Boltzmann se escribe
Definición de temperatura
Supongamos que transferimos una cantidad de calor q al sistema y como consecuencia una partícula pasa del nivel Ej al nivel Ek, q=Ek-Ej.
El número de micoestados Ω cambia, la relación ahora es
El cambio en Ω que experimenta el sistema cuando le transferimos una pequeña cantidad de calor q depende solo de q, y no de la disposición de los niveles de energía, de cuantos niveles de energía hay accesibles, del espaciado entre los niveles, o si es una o más partículas las que cambian de nivel. Tomando logaritmos neperianos llegamos a la expresión equivalente
Equilibrio térmico. Definición de temperatura
Consideremos ahora dos sistemas en equilibrio. El primero, tiene una NA partículas y una energía UA. La distribución de las partículas entre sus niveles de energía está dada por
El segundo, tiene NB partículas y una energía UB. La distribución de las partículas entre sus niveles de energía está dada por
Supongamos que βA≠ βB. El número de microestados del sistema compuesto por los dos subsistemas A y B es
Ω=ΩA·ΩB, o bien, lnΩ=lnΩA+lnΩB
Como el sistema compuesto no estará en equilibrio, la transferencia de energía tiene lugar en aquella dirección en la que Ω se haga máximo.
Supongamos que una cantidad de calor q se transfiere desde el subsistema A al subsistema B, de modo que B gana una cantidad de calor q, por lo que su cambio en el número de microestados ΩB es
Δ(lnΩB)=βB·q
El subsistema A pierde una cantidad de calor por lo que el cambio en el número de micoestados ΩA es
Δ(lnΩA)=-βA·q
El cambio en el número de micorestados Ω del sistema será
Δ(lnΩ)= Δ(lnΩA)+ Δ(lnΩB)=-βA·q +βB·q =(βB-βA )·q
Para que el sistema tienda hacia el equilibrio, se ha incrementar Ω del sistema combinado, el calor q se transferirá de forma espontánea desde el subsistema A al subsistema B, si βA<βB. En cambio, si βA=βB el valor de Ω del sistema combinado no cambia apreciablemente, el sistema está en equilibrio
Se llega así a dos importantes conclusiones relativas al significado físico del parámetro β .
- Si βA<βB el sistema combinado no está en equilibrio y se transfiere energía de forma espontánea del subsistema A al B.
- Si βA=βB el sistema combinado está en equilibrio.
Por convención se asigna al subsistema A que suministra energía una temperatura TA más alta que al subsistema que recibe energía TB, se dice que A está más caliente y B más frío. La temperatura y el parámetro β están inversamente relacionados.
donde k=1.3805·10-23 J/ºK es la constante de Boltzmann cuando T se expresa en la escala kelvin de temperaturas.
Como sabemos, la temperatura de un cuerpo se asocia al cambio en alguna de sus propiedades, denominada propiedad termométrica, por ejemplo, la longitud o el volumen.
Las dos conclusiones anteriores se redefinen en términos de la temperatura
- Si TA>TB el sistema combinado no está en equilibrio y se transfiere energía de forma espontánea del subsistema A al B.
- Si TA=TB el sistema combinado está en equilibrio.
Definición de entropía
En el apartado anterior, mostramos que cuando un sistema recibe una cantidad de calor q el número de microestados cambia
Δ(lnΩ)=βq
o expresando en términos de la temperatura T.
Tenemos una relación entre una cantidad microscópica (el número de microestados Ω) y dos cantidades macroscópicas: la energía transferida q y la temperatura T. La parte derecha de la igualdad es la definición termodinámica de variación de entropía ΔS.
Llegamos así a la definición de entropía en términos del número de micoroestados Ω asociados con un macroestado dado del sistema
S=k·lnΩ
Procesos irreversibles. Principio de incremento de entropía
Consideremos, de nuevo, un sistema formado por dos subsistemas A y B, el número de microestados del sistema combinado es Ω=ΩA·ΩB , tomando logaritmos neperianos y a partir de la definición de entropía llegamos a
S=SA+SB
La entropía es una magnitud aditiva, ya que la entropía del sistema combinado es la suma de las entropías de los subsistemas A y B que lo forman.
Calculemos ahora la variación de entropía cuando una cantidad de calor q se transfiere de forma espontánea desde el subsistema A a temperatura TA hacia el subsistema B a temperatura TB.
El subsistema A disminuye su entropía, pero aumenta la de B. Como TA>TB, el cambio de entropía ΔS>0 del sistema combinado es positivo, su entropía aumenta.
Si inicialmente los subsistemas A y B están en equilibrio, al ponerlos en contacto el sistema combinado deja de estar en equilibrio. El número de microestados P=ΩA·ΩB tiende hacia un valor máximo. Por esta razón la energía fluye espontáneamente desde un cuerpo caliente hacia uno frío cuando se ponen en contacto y nunca ocurre el proceso inverso.
Referencias
Schoept D. C. A statistical development of entropy for the introductory physics course. Am. J. Phys. 70(2) February 2002, pp. 128-136.
Alonso-Finn, Física V-III, Fundamentos Cuánticos y Estadísticos. Edt. Fondo Educativo Interamericano (1971), págs. 446-462.

