Atmósfera isoterma

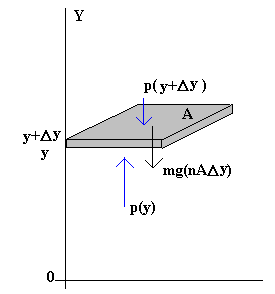
Examinemos las fuerzas sobre un pequeño volumen sección A y de espesor Δy comprendido entre las alturas y e y+Δy. La fuerza de la gravedad sobre esta porción de la atmósfera es

F_y=-mg(N·A·Δy)

Donde m es la masa de una molécula y N es el número de moléculas por unidad de volumen, que es una función de la altura y.

La fuerza F_y es compensada por la diferencia de presión en las altitudes y e y+Δy, tal como se ve en la figura.

${\displaystyle \left(p(y+\Delta y)-p(y)\right)A=-mg(N·A·\Delta y)}$

o bien,

${\displaystyle \frac{p(y+\Delta y)-p(y)}{\Delta y}=-Nmg}$

En el límite cuando Δy tiende a cero, obtenemos la derivada de la presión

${\displaystyle \frac{dp}{dy}=-Nmg}$

Si consideramos la atmósfera como un gas ideal, se cumple que p=NkT, para una unidad de volumen

${\displaystyle \begin{array}{l}kT\frac{dN}{dy}=-Nmg\\ \frac{dN}{dy}=-\frac{mg}{kT}dy\end{array}}$

Integrando

${\displaystyle \begin{array}{l}{\displaystyle \underset{N_0}{\overset{N}{\int }}\frac{dN}{N}}=-\frac{mg}{kT}{\displaystyle \underset{0}{\overset{y}{\int }}dy}\\ \ln N-\ln N_0=-\frac{mg}{kT}y\\ N=N_0\exp \left(-\frac{mg}{kT}y\right)\end{array}}$

El número de moléculas por unidad de volumen N decrece exponencialmente con la altura. Es importante destacar que el numerador en la función exponencial mgy representa la energía potencial de las moléculas individuales con respecto al nivel del mar. Por tanto, la distribución de moléculas con la altura y sigue la ley de Boltzmann.

Presión

• La masa molecular de aire es M=0.0288 kg/mol, la masa de una molécula m=M/N_A. donde N_A=6.0225·10²³ moléculas/mol es el número de Avogadro

• La constante R=kN_A=8.3143 J/(K·mol) de los gases es el producto del número de Avogadro por la constante k=1.3805·10^-23 J/K de Boltzmann

Partimos de la ecuación

${\displaystyle \begin{array}{l}N=N_0\exp \left(-\frac{mg}{kT}y\right)\\ \frac{p}{kT}=\frac{p_0}{kT}\exp \left(-\frac{M}{N_A}\frac{g}{kT}y\right)\\ p=p_0\exp \left(-\frac{Mg}{RT}y\right)\end{array}}$

donde p₀ es la presión a nivel del mar, y=0.

Se denomina H al cociente

${\displaystyle p=p_0\exp \left(-\frac{y}{H}\right),H=\frac{RT}{Mg}}$

La presión disminuye exponencialmente con la altura para una atmósfera isoterma

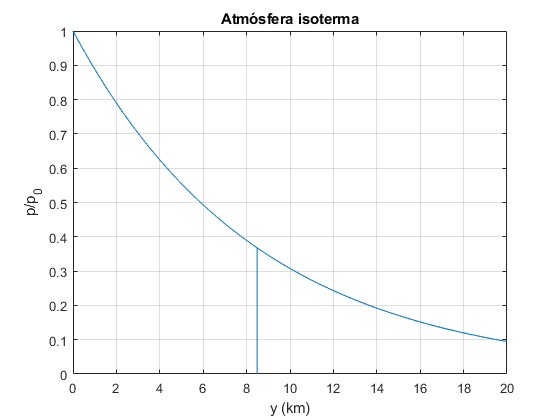
Representamos el cociente p/p₀ en función de y. Señalamos la altura H=8.4840 km mediante una línea vertical para una temperatura T=288 K

H=8.484; %en km
f=@(y) exp(-y/H);
fplot(f ,[0,20])
line([H,H],[0,f(H)])
grid on
xlabel('y (km)')
ylabel('p/p_0')
title ('Atmósfera isoterma')

En las siguientes tablas, se proporciona la presión en Pa y la temperatura en K, medidas cada medio km hasta 20 km de altura

Fuente: Properties Of The U.S. Standard Atmosphere 1976. Table 2

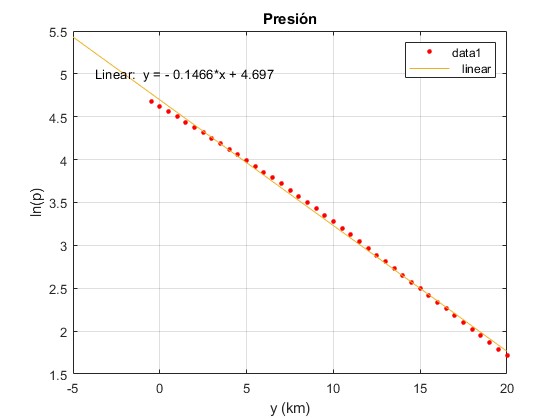
Representamos los datos de lnp en función de la altura y en km mediante puntos de color rojo.

Cuando aparece Figure 1, seleccionamos en el menú Tools/Basic Fitting. En TYPES OF FIT, activamos la casilla Linear. Se traza la recta de regresión lnp=-0.1466y+4.697

y=-0.5:0.5:20;
p=[107477, 101325, 95461, 89876, 84559, 79501, 74691, 70121, 65780, 61660, 
57752, 54048, 50539, 47217, 44075, 41105, 38299, 35651, 33154, 30800, 
28584, 26499, 24540, 22699, 20984, 19399, 17933, 16579, 15327, 14170, 
13100, 12111, 11197, 10352, 9571, 8849, 8182, 7565, 6994, 6467, 5979, 5529]/1000; 
plot(y,log(p),'ro','markersize',3,'markerfacecolor','r')
grid on
xlabel('y (km)')
ylabel('ln(p)')
title('Presión')

La pendiente de la recta m=0.0001466 cuando la altura y se expresa en m en vez de km

${\displaystyle \begin{array}{l}\frac{Mg}{RT}=\frac{0.0288·9.8}{8.3143·T}=0.0001466\\ T=231.6\text{K}\end{array}}$

M=0.0288 kg/mol es la masa molecular del aire y R=8.3143 J/(K·mol) es la constante de los gases

La atmósfera isoterma nos da una temperatura de 231.6 K. En las tablas vemos que la temperatura disminuye hasta que alcanza un valor constante a una altura y=11.5 km

y=-0.5:0.5:20;
T=[291.4,288.1,284.9,281.7,278.4,275.2,271.9,268.7,265.4,262.2,
258.9,255.7,252.4,249.2,245.9,242.7,239.5,236.2,233.0,229.7,226.5, 
223.3, 220.0, 216.8,216.6,216.6,216.6,216.6,216.6,216.6,216.6,
216.6,216.6,216.6,216.6,216.6,216.6,216.6,216.6,216.6,216.6,216.6];
plot(y,T,'ro','markersize',3,'markerfacecolor','r')
T_m=sum(T)/length(T); %temperatura media
line([-0.5,20],[T_m,T_m])
grid on
xlabel('y (km)')
ylabel('T (K)')
title('Temperatura')
disp(T_m)

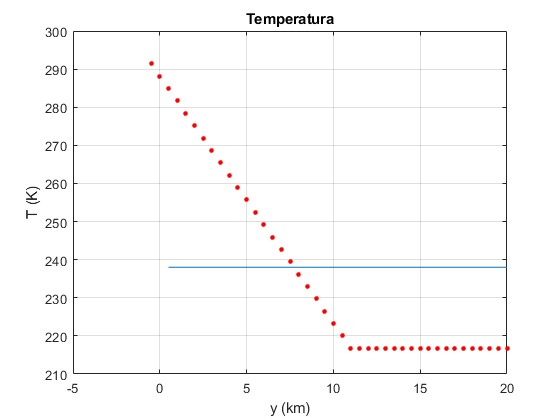
La temperatura media es 238 K

238.0119

La gravedad varía con la altura

La aceleración de la gravedad g no es constante sino que disminuye con la altura y

${\displaystyle g=G\frac{M}{r^2}=G\frac{M}{R^2}\frac{1}{{\left(1+y/R\right)}^2}=\frac{g_0}{{\left(1+y/R\right)}^2}}$

donde g₀ es la aceleración de la gravedad a nivel del mar, 9.8 m/s²

Integramos la ecuación diferencial

${\displaystyle \frac{dn}{dy}=-n\frac{m}{kT}\frac{g_0}{{\left(1+y/R\right)}^2}}$

con las condiciones iniciales y=0, n=n₀

${\displaystyle \begin{array}{l}{\displaystyle \underset{n_0}{\overset{n}{\int }}\frac{dn}{n}}=-\frac{m{g}_0}{kT}{\displaystyle \underset{0}{\overset{y}{\int }}\frac{dy}{{\left(1+y/R\right)}^2}}\\ \ln \frac{n}{n_0}=-\frac{m{g}_{0}R}{kT}\left(1-\frac{R}{R+y}\right)\\ p=p_0\exp \left\{-\frac{1}{1+y/R}\frac{y}{H}\right\}\end{array}}$

Efecto de la rotación de la Tierra

La gravedad es máxima en el polo y mínima en el ecuador, debido a la rotación de la Tierra con velocidad angular ω=2π/(24·60·60) rad/s

Supongamos que la atmósfera en equilibrio gira solidariamente con la Tierra a la misma velocidad angular. En el ecuador, la acelación de la gravedad es

${\displaystyle g=\frac{g_0}{{\left(1+y/R\right)}^2}-{\omega }^{2}R\left(1+y/R\right)}$

Dado que ω²R/g₀=3.44·10^-3, el efecto de la rotación será muy pequeño a bajas alturas

${\displaystyle \begin{array}{l}{\displaystyle \underset{n_0}{\overset{n}{\int }}\frac{dn}{n}}=-\frac{m}{kT}{\displaystyle \underset{0}{\overset{y}{\int }}\left\{\frac{g_0}{{\left(1+y/R\right)}^2}-{\omega }^{2}R\left(1+y/R\right)\right\}dy}\\ \ln \frac{n}{n_0}=-\frac{m}{kT}\left\{g_{0}R\left(1-\frac{R}{R+y}\right)-{\omega }^{2}Ry\left(1+\frac{y}{2R}\right)\right\}\\ p=p_0\exp \left\{\left(-\frac{1}{1+y/R}+\frac{{\omega }^{2}R}{g_0}\left(1+\frac{y}{2R}\right)\right)\frac{y}{H}\right\}\end{array}}$

Representamos el cociente p/p₀ para una atmósfera isoterma a la temperatura de 288 K (15°). La atmósfera isoterma es aplicable hasta 6 km de altura, sin error apreciable y también en una zona alrededor de 20 km de altura donde la temperatura es constante 217 K (-56°).

H=8420;
R=6370*1000; %radio de la Tierra
hold on
%gravedad constante
f=@(y) exp(-y/H);
fplot(f,[0,6000]);
%gravedad varía con la altura
g=@(y) exp(-y./(H*(1+y/R)));
fplot(g,[0,6000]);
%efecto de la rotación y de la gravedad
w2R=(2*pi/(24*60^2))^2*R;
gr=@(y) exp((-1./(1+y/R)+w2R*y.*(1+y/(2*R))/(9.8*H)).*y/H);
fplot(gr,[0,6000]);
hold off
grid on
xlabel('h(m)')
ylabel('p/p_0')
legend('constante','variable','variable+rotación')
title('Atmósfera isoterma')

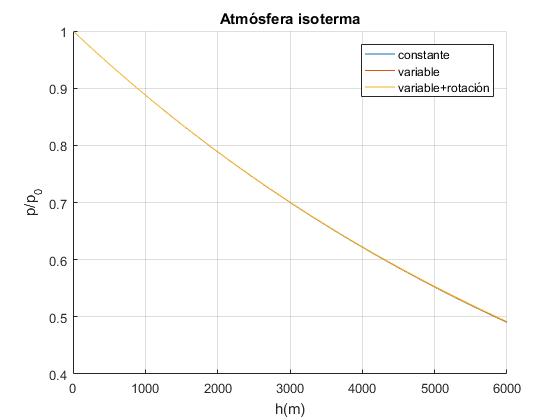
El efecto de la variación de la gravedad con la altura y de la rotación es inperceptible en la representación gráfica, para bajas alturas, menores de 6 km. Para alturas elevadas y=0.01·R=63.7 km, se aprecian algunas diferencias entre los valores de las tres funciones que describen:

• f, la gravedad constante
• g, la gravedad disminuye con la altura
• gr, la gravedad disminuye con la altura combinada con el efecto de la rotación de la Tierra en el ecuador

>> g(0.01*R)/f(0.01*R)
ans =    1.0778
>> gr(0.01*R)/f(0.01*R)
ans =    1.3134

Variación de la presión con la profundidad

Supongamos que excavamos un túnel en la dirección del centro de la Tierra, vamos a calcular como varía la presión con la profundidad y<0

En la página titulada La aceleración de la gravedad en el interior y en el exterior de una distribución esférica y uniforme de masa calculamos la aceleración de la gravedad g a una distancia r=R+y del centro de la Tierra, o a una profundidad y<0.

${\displaystyle g=GM\frac{r}{R^3}=g_0\left(1+\frac{y}{R}\right)}$

Integramos la ecuación diferencial

${\displaystyle \frac{dn}{dy}=-n\frac{m}{kT}{g}_0\left(1+y/R\right)}$

con las condiciones iniciales y=0, n=n₀

${\displaystyle \begin{array}{l}{\displaystyle \underset{n_0}{\overset{n}{\int }}\frac{dn}{n}}=-\frac{m{g}_0}{kT}{\displaystyle \underset{0}{\overset{y}{\int }}\left(1+y/R\right)dy}\\ \ln \frac{n}{n_0}=-\frac{m{g}_0}{kT}y\left(1+\frac{y}{2R}\right)\\ p=p_0\exp \left\{-\left(1+\frac{y}{2R}\right)\frac{y}{H}\right\}\end{array}}$

H=8420;
R=6370*1000; %radio de la Tierra
f=@(y) exp(-(1+y/(2*R)).*y/H);
fplot(f,[-6000,0]);
grid on
xlabel('h(m)')
ylabel('p/p_0')
title('Atmósfera isoterma')

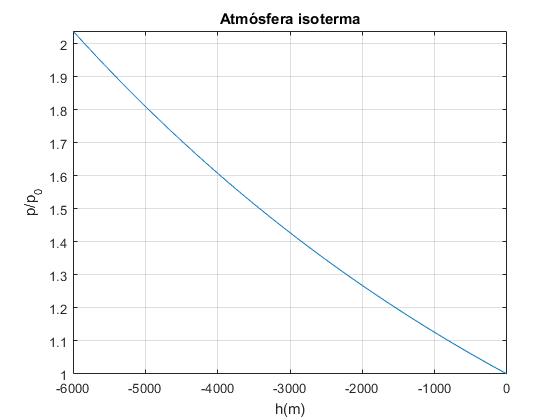
Calculamos la presión a las profundidades y=-5.8 km, -58 km y en el centro de la Tierra -6370 km

>> f(-5800)
ans =    1.9908
>> f(-58000)
ans =  950.5124
>> f(-R)
ans =  1.9004e+164

La atmósfera adiabática

La suposición de que la temperatura de la atmósfera es la misma para cualquier altura no es correcta. En el avión nos informan que la temperatura exterior es muy baja cuando el avión vuela a gran altura. La temperatura en general no varía linealmente con la altura, sino de forma más compleja dependiendo de la capa atmosférica. Por ejemplo, la troposfera que es una capa que se extiende desde 12 km a 16 km de altura, la temperatura disminuye a razón de a=-6.5 ºC/km. Entre 20 y 32 km, debido a la capa de ozono, la temperatura aumenta a razon de a=-1 K/km

Partimos de la relación

${\displaystyle \frac{dp}{dy}=-Nmg}$

Si consideramos la atmósfera como un gas ideal, se cumple que p=NkT, para una unidad de volumen

${\displaystyle \begin{array}{l}\frac{dp}{dy}=-\frac{p}{kT}mg\\ \frac{dp}{p}=-\frac{Mg}{RT}dy\end{array}}$

En una transformación adiabática

${\displaystyle \begin{array}{l}{p}^{1-\gamma }{T}^{\gamma }=\text{cte}\text{,}\gamma \text{=}\frac{c_p}{c_v},c_p-c_v=R\\ \left(1-\gamma \right)\ln p+\gamma \ln T=\text{cte}\end{array}}$

Derivando

${\displaystyle \left(1-\gamma \right)\frac{dp}{p}+\gamma \frac{dT}{T}=0}$

La variación de temperatura T con la altura y es

${\displaystyle \begin{array}{l}-\left(1-\gamma \right)\frac{Mg}{RT}dy+\gamma \frac{dT}{T}=0\\ \frac{dT}{dy}=\frac{1-\gamma }{\gamma }\frac{Mg}{R}=-\frac{R}{c_p}\frac{Mg}{R}=-\frac{Mg}{c_p}\\ {\displaystyle \underset{T_0}{\overset{T}{\int }}dT}=-\frac{Mg}{c_p}{\displaystyle \underset{0}{\overset{y}{\int }}dy}\\ T=T_0-\frac{Mg}{c_p}y\end{array}}$

La temperatura disminuye linealmente con la altura

La variación de la presión p con la altura y es

${\displaystyle \begin{array}{l}{p}^{1-\gamma }{T}^{\gamma }=\text{cte}\\ p_0^{1-\gamma }{T}_0^{{}^{\gamma }}=p^{1-\gamma }{\left(T_0-\frac{Mg}{c_p}y\right)}^{\gamma }\\ p^{1-\gamma }=\frac{p_0^{1-\gamma }{T}_0^{{}^{\gamma }}}{{\left(T_0-\frac{Mg}{c_p}y\right)}^{\gamma }}=p_0^{1-\gamma }\frac{1}{{\left(1-\frac{Mg}{c_p{T}_0}y\right)}^{\gamma }}\\ p=p_0{\left(\frac{1}{{\left(1-\frac{Mg}{c_p{T}_0}y\right)}^{\gamma }}\right)}^{\frac{1}{1-\gamma }}=p_0{\left(1-\frac{Mg}{c_p{T}_0}y\right)}^{\frac{-\gamma }{1-\gamma }}=p_0{\left(1-\frac{Mg}{c_p{T}_0}y\right)}^{\frac{c_p}{R}}\end{array}}$

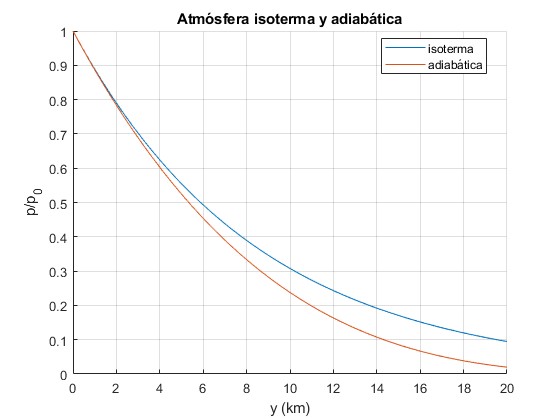
En la figura, se compara la variación de la presión p/p₀ con la altura y hasta 20 km, en el caso de una atmósfera isoterma y para una atmósfera adiabática

Datos

• Masa molecular del aire, M=0.0288 kg/mol
• Calor específico del aire a presión constante, c_p=1.012 J/(g·K)
• Temperatura a nivel del mar y=0, T₀=288 K

R=8.3143; %constante de los gases
M=0.0288; %masa molecular del aire kg/mol
cp=1.012*M*1000; %calor específico a presión constante J(Kmol)
T0=288; %temperatura para y=0;
H=R*T0/(M*9.8);
hold on
f=@(y) exp(-y*1000/H); %isoterma
fplot(f ,[0,20])
k=M*9.8/(cp*T0);
g=@(y) (1-k*y*1000).^(cp/R); %adiabática
fplot(g ,[0,20])
hold off
grid on
legend('isoterma','adiabática','location','best')
xlabel('y (km)')
ylabel('p/p_0')
title ('Atmósfera isoterma y adiabática')

La atmósfera estándar

En la página web de la NASA (National Aeronautics and Space Administration) titulada Earth Atmosphere model se describe un modelo de atmósfera que consta de tres zonas. La altura h se da en metros, la temperatura T en gardos centígrados y la presión p en kilo pascals

• Por debajo de 11000 m de altura. La temperatura disminuye linealmente y la presión disminuye

T=15.04-0.00649·h
p=101.29·[(T+273.1)/288.08]^5.256

• De 11000 m a 25000 m de altura. La temperatura es constante y la presión disminuye exponencialmente

T=-56.46
p=22.65·exp(1.73-0.000157·h)

• Por encima 25000 m de altura. La temperatura aumenta ligeramente y la presión disminuye

T=-131.21+0.00299 ·h
p=2.488·[(T+273.1)/216.6]^-11.388

La ecuación de estado relaciona la densidad ρ con la presión p y la temperatura T

ρ=p/[0.2869·(T+273.1)]

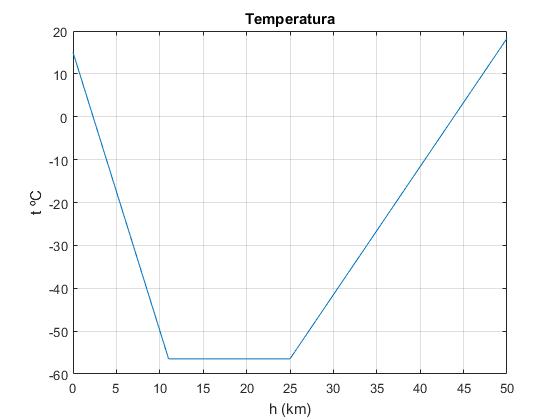
Representamos la temperatura T en grados centígrados en función de la altura h en km

h=0:100:50000; %altura hasta 50 km
T=(h<11000).*(15.04-0.00649*h)+(h>=11000 & h<25000).*(-56.46)+
(h>=25000).*(-131.21+0.00299*h);
plot(h/1000,T)
grid on
xlabel('h (km)')
ylabel('t °C')
title('Temperatura')

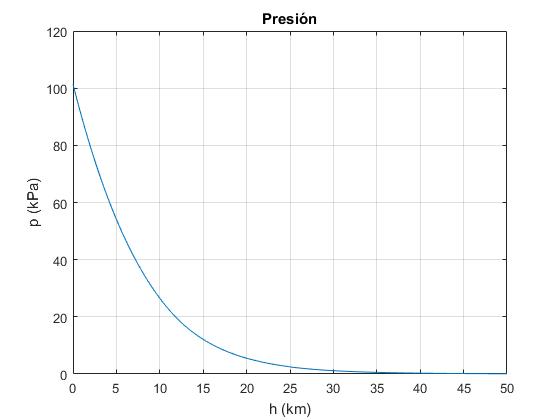
Representamos la presión p en kilo pascal en función de la altura h en km

h=0:100:50000; %altura hasta 50 km
zona1=h<11000;
zona2=h>=11000 & h<25000;
zona3=h>=25000;
T=zona1.*(15.04-0.00649*h)+zona2.*(-56.46)+zona3.*(-131.21+0.00299*h);

p=zona1.*(101.29*((T.*zona1+273.1)/288.08).^5.256)+
zona2.*(22.65*exp(1.73-.000157*h.*zona2))
+zona3.*(2.488*((T.*zona3+273.1)/216.6).^-11.388);
plot(h/1000,p)
grid on
xlabel('h (km)')
ylabel('p (kPa)')
title('Presión')

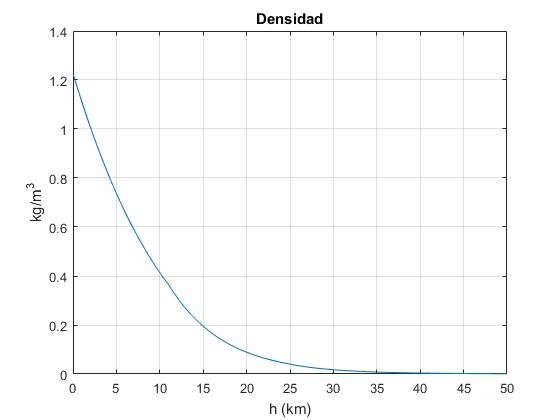
Representamos la densidad ρ en kg/m³ en función de la altura h en km

h=0:100:50000; %altura hasta 50 km
zona1=h<11000;
zona2=h>=11000 & h<25000;
zona3=h>=25000;
T=zona1.*(15.04-0.00649*h)+zona2.*(-56.46)+zona3.*(-131.21+0.00299*h);
p=zona1.*(101.29*((T.*zona1+273.1)/288.08).^5.256)+
zona2.*(22.65*exp(1.73-.000157*h.*zona2))
+zona3.*(2.488*((T.*zona3+273.1)/216.6).^-11.388);

rho=zona1.*(p.*zona1./(0.2869*(T.*zona1+273.1)))+
zona2.*(p.*zona2./(0.2869*(T.*zona2+273.1)))
+zona3.*(p.*zona3./(0.2869*(T.*zona3+273.1)));
plot(h/1000,rho)
grid on
xlabel('h (km)')
ylabel('kg/m^3')
title('Densidad')

Máxima fuerza de rozamiento

Cuando un cuerpo se mueve en el seno de un fluido, experimenta una fuerza de rozamiento que tiene la expresión

${\displaystyle F_r=C_D\frac{1}{2}{\rho }_{f}A{v}^2}$

Donde C_D se denomina coeficiente de arrastre, ρ_f es la densidad del fluido, A es el área de la sección transversal a la dirección del movimiento y v es la velocidad relativa del objeto respecto del fluido. La fuerza de rozamiento F_r es poporcional a la densidad del aire y al cuadrado de la velocidad

Para un cohete que despega verticalmente, la densidad del aire disminuye rápidamente con la altura h. El cohete parte del reposo y aumenta rápidamente su velocidad v, por tanto, habrá un momento para el cual, la fuerza de rozamiento F_r alcanza máximo valor.

Hasta 11000 metros se puede expresar la densidad ρ en función de la altura h

${\displaystyle \begin{array}{l}\rho =\frac{101.29{\left(\frac{\left(T+273.1\right)}{288.08}\right)}^{5.256}}{101.29\left(T+273.1\right)}=\frac{101.29}{101.29·{288.08}^{5.256}}{\left(T+273.1\right)}^{4.256}=\\ \frac{101.29}{101.29·{288.08}^{5.256}}{\left(15.04-0.00649h+273.1\right)}^{4.256}\end{array}}$

De la forma

${\displaystyle \rho ={\rho }_0{\left(1-\frac{h}{H}\right)}^n}$

Donde ρ₀=1.2266 kg/m³ es la densidad del aire en el suelo, H=44397 m y n=4.256

Sean x y v la altura y velocidad vertical del cohete en el instante t. Calculamos el máximo de una función proporcional a la densidad ρ y al cuadrado de la velocidad v

${\displaystyle \begin{array}{l}f=\rho v^2={\rho }_0{\left(1-\frac{x}{H}\right)}^n{v}^2\\ \frac{df}{dt}={\rho }_{0}n\left(-\frac{v}{H}\right){\left(1-\frac{x}{H}\right)}^{n-1}{v}^2+2{\rho }_0{\left(1-\frac{x}{H}\right)}^{n}v\frac{dv}{dt}=0\\ -n\frac{v^2}{H}+2\left(1-\frac{x}{H}\right)\frac{dv}{dt}=0\end{array}}$

El caso más sencillo, se presenta cuando el cohete, se mueve verticalmente con aceleración a constante. Su velocidad es v=at y la altura es x=at²/2 en el instante t.

${\displaystyle t=\sqrt{\frac{2H}{(n+1)a}}}$

Por ejemplo, suponiendo una aceleración constante de alrededor de 6.5 m/s², el instante t en el que la fuerza de rozamiento alcanza su máximo valor es 51 s, el cohete se encuentra a una altura de 8450 m. En un vuelo real, el cohete sube verticalmente, después se va inclinando, la aceleración se va incrementando a medida que va gastando el combustible y pierde peso.

En la página titulada Movimiento vertical de un cohete se deducen las expresiones de la posición x, velocidad v y aceleración dv/dt en función del tiempo, de un cohete de masa m₀ al despegar y empuje constante uD. Al sustituirlos en la última ecuación, obtenemos una ecuación transcendente en t que hemos de resolver por procedimientos numéricos.

Referencias

Mario N. Berberan-Santos, Evgeny N. Bodunov, Lionello Pogliani. On the barometric formula inside the Earth. J Math Chem (2010) 47; 990-1004

Masatsugu Sei Suzuki. Adiabatic atmosphere. September 07, 2017

Philip Backman. Maximum Aerodynamic Force on a Ascending Space Vehicle. The Physics Teacher. Vol. 50, March 2012, pp. 167-169