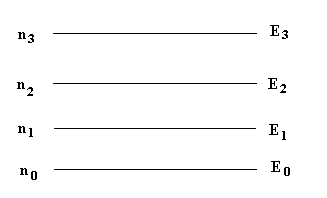
Sea un sistema cuyas partículas pueden ocupar un conjunto de niveles discretos E₀, E₁, E₂, ..., y sean n₀, n₁, n₂, ... la proporción de partículas que ocupan cada nivel a una temperatura dada T. La relación entre los números n_i y la energía E_i viene dada por la fórmula de la estadística clásica

n_i=c·exp(-E_i/kT)

k es la constante de Boltzmann 1.38·10^-23 J/K.

El valor de la constante c se determina a partir de la condición de que la suma de todos los números n_i debe se la unidad. El valor de n_i es por tanto.

${\displaystyle n_i=\frac{\exp \left(\frac{-E_i}{kT}\right)}{{\displaystyle \sum _0^{N-1}\exp \left(\frac{-E_i}{kT}\right)}}}$

La energía media <E> de las partículas es

${\displaystyle <E>={\displaystyle \sum _0^{N-1}{n}_i{E}_i}}$

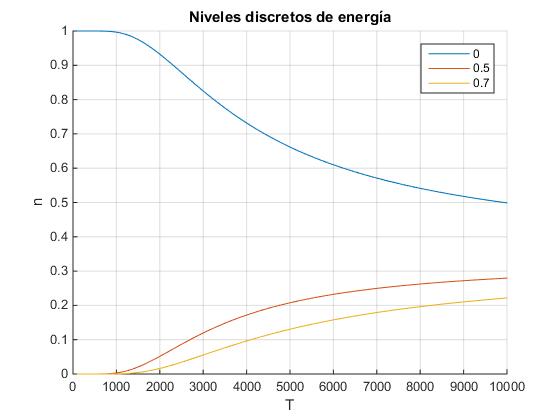
Sea un sistema en el que las partículas pueden ocupar tres niveles de energía: E₀=0, E₁=0.5, E₂=0.7 eV. Vamos a determinar la proporción de partículas n₀, n₁, n₂ que ocupan cada nivel a varias temperaturas. Observaremos que cuando la temperatura T es baja casi todas las partículas están en el nivel más bajo de energía

cte=1.6e-19/1.3805e-23; %eV/k
E=[0,0.5,0.7]; %niveles de energía en eV
n=zeros(1,101);
i=0;
for T=0:100:10000;
    z=0;
    for e=E
        z=z+exp(-e*cte/T);
    end
    i=i+1;
    j=0;
    for e=E
        j=j+1;
        n(i,j)=exp(-e*cte/T)/z;
    end
end
hold on
for j=1:length(E)
    plot(0:100:10000,n(:,j),'displayName',num2str(E(j)))
end
grid on
legend('-DynamicLegend','location','northeast')
xlabel('T')
ylabel('n')
title('Niveles discretos de energía')

Vibraciones de las moléculas diatómicas

Resolviendo la ecuación de Schrödinger de un oscilador armónico cuántico hallamos que los niveles de energía dados por la expresión.

${\displaystyle E=\hslash {\omega }_0\left(n+\frac{1}{2}\right)n=\text{0}\text{, 1}\text{, 2}\mathrm{,3...}}$

Siendo ω₀ la frecuencia natural del oscilador armónico

En esta sección vamos a calcular la distribución de las moléculas de un gas diatómico entre dichos niveles de energía a una temperatura dada T.

Al ser los niveles de energía equidistantes, la representación mediante un diagrama de barras de la proporción de moléculas que ocupan cada uno de los niveles de energía, nos dará una visión directa del carácter exponencial decreciente de la energía de la ley de Boltzmann.

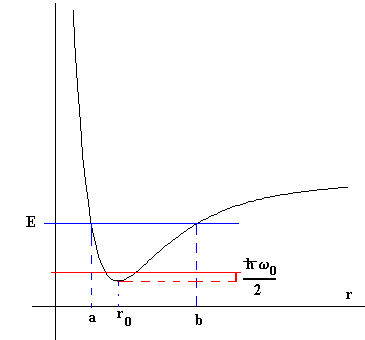
Consideremos una molécula diatómica que tiene una energía potencial como la que se muestra en la figura. Si el movimiento de los núcleos de la molécula corresponde a una energía E, éstos oscilan de modo que clásicamente su separación varía entre Oa y Ob. Sin embargo, se debe describir el movimiento de los núcleos desde el punto de vista de la Mecánica Cuántica. Representamos aproximadamente la parte inferior de la curva, por la parábola $\frac{1}{2}k{\left(r-r_0\right)}^2$ , siendo r₀ la separación de equilibrio, el mínimo de la curva de la energía potencial. En dicha región, el movimiento oscilatorio relativo de los núcleos sería armónico simple, con una frecuencia natural de oscilación de ${\omega }_0^2=k/\mu$ , siendo μ la masa reducida de la molécula.

El nivel i tiene una energía que viene dada por la expresión

${\displaystyle E_i=\hslash {\omega }_0\left(i+\frac{1}{2}\right)i=\text{0}\text{, 1}\text{, 2}\mathrm{,3...}}$

En consecuencia, los niveles vibracionales de energía de las moléculas son equidistantes.

En la siguiente tabla, se da el intervalo de energía en electrón-voltios, correspondiente a la separación entre dos niveles consecutivos, $\hslash {\omega }_0$, de las moléculas.

La proporción de moléculas que ocupan un nivel dado de energía i es

${\displaystyle n_i=C\exp \left(-\frac{\hslash {\omega }_0\left(i+\frac{1}{2}\right)}{kT}\right)}$

que expresamos como

${\displaystyle n_i=C{e}^{-x/2}{e}^{-ix}x=\frac{\hslash {\omega }_0}{kT}}$

Calculamos la constante C a partir de la condición de que ${\displaystyle \sum _0^{\infty }{n}_i=1}$

Tenemos la suma de los infinitos términos de una progresión geométrica de razón e^-x.

${\displaystyle C{e}^{-x/2}\frac{1}{1-e^{-x}}=1}$

La expresión de la proporción n_i de moléculas que ocupan un nivel dado i de energía queda finalmente

${\displaystyle n_i=\left(1-e^{-x}\right)e^{-ix}x=\frac{\hslash {\omega }_0}{kT}}$

cte=1.6e-19/1.3805e-23; %eV/k
%['Anhídrido carbónico (CO)', 'Hidrógeno (H2)', 'Oxígeno (O2)', 
'Nitrógeno (N2)', 'Cloro (Cl2)', 'Acido clorhídrico (ClH)'];  
constantes=[0.268, 0.543, 0.194, 0.292, 0.0698, 0.369];
indice=1; %cambiar de sustancia
T=4000; %cambiar la temperatura 
x=constantes(indice)*cte/T;
i=0:6;  %niveles
y=constantes(indice)/2+constantes(indice)*i;
n=(1-exp(-x))*exp(-i*x);
hold on
for z=y
    line([0,1],[z,z]);
end
barh(y,n, 0.2)
hold off
grid on
xlabel('n')
ylabel('E')
title('Niveles vibracionales')

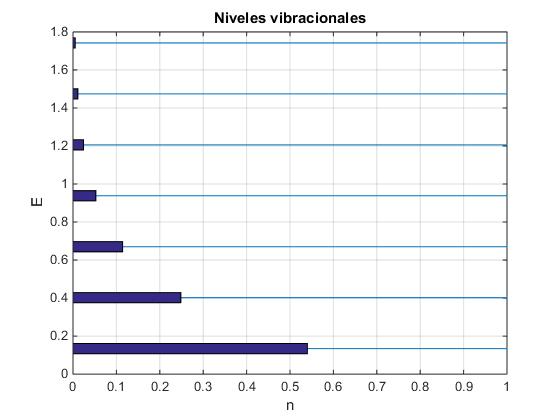
>> n
n =    0.5400    0.2484    0.1143    0.0526    0.0242    0.0111    0.0051
>> sum(n)
ans =    0.9956

En la figura se muestran los niveles de energía de la molécula Anhídrido carbónico (CO), indice=1. Mediante las barras horiontales se muestra la proporción de partículas en cada uno de los niveles

Energía interna y capacidad calorífica

Calculamos la función de partición Z

${\displaystyle Z={\displaystyle \sum _{i=0}^{\infty }\exp \left(-\frac{\hslash {\omega }_0}{kT}\left(i+\frac{1}{2}\right)\right)}=\exp \left(-\frac{\hslash {\omega }_0}{2kT}\right){\displaystyle \sum _{i=0}^{\infty }\exp \left(-\frac{\hslash {\omega }_0}{kT}i\right)}}$

Tenemos la suma de los infinitos términos de una progresión geométrica de razón e^-x.

${\displaystyle \begin{array}{l}Z=\exp \left(-\frac{x}{2}\right){\displaystyle \sum _{i=0}^{\infty }\exp \left(-xi\right)}=\exp \left(-\frac{x}{2}\right)\frac{1}{1-\exp (-x)}=\frac{1}{\exp \left(x/2\right)-\exp \left(-x/2\right)}\\ =\frac{2}{\sinh \left(x/2\right)}=\frac{2}{\sinh \left(\frac{\hslash {\omega }_0}{2kT}\right)}\end{array}}$

Conocida Z calculamos la energía interna U de las N moléculas. Teniendo en cuenta que β=1/kT

${\displaystyle \begin{array}{l}U=-N\frac{\partial \ln Z}{\partial \beta }=N\frac{\partial \ln \left(\sinh \left(\frac{1}{2}\beta \hslash {\omega }_0\right)\right)}{\partial \beta }=\frac{N}{\sinh \left(\frac{1}{2}\beta \hslash {\omega }_0\right)}\frac{\hslash {\omega }_0}{2}\cosh \left(\frac{1}{2}\beta \hslash {\omega }_0\right)\\ U=N\frac{\hslash {\omega }_0}{2}\coth \left(\frac{\hslash {\omega }_0}{2kT}\right)\end{array}}$

Teniendo en cuenta la relación

${\displaystyle \frac{e^{x/2}+e^{-x/2}}{e^{x/2}-e^{-x/2}}=\frac{e^x+1}{e^x-1}=2\left(\frac{1}{2}+\frac{1}{e^x-1}\right)}$

Expresamos la energía interna U de otra forma equivalente

${\displaystyle U=N\hslash {\omega }_0\left(\frac{1}{2}+\frac{1}{\exp \left(\frac{\hslash {\omega }_0}{kT}\right)-1}\right)}$

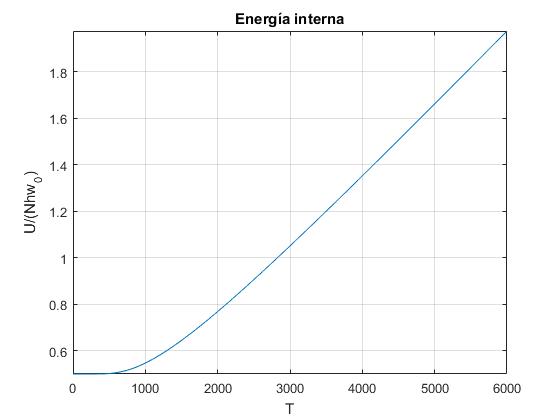
Representamos U/(Nhω₀), en función de la temperatura T

cte=1.6e-19/1.3805e-23; %eV/k
%['Anhídrido carbónico (CO)', 'Hidrógeno (H2)', 'Oxígeno (O2)', 'Nitrógeno (N2)',
 'Cloro (Cl2)', 'Acido clorhídrico (ClH)'];  
constantes=[0.268, 0.543, 0.194, 0.292, 0.0698, 0.369];
indice=1; %cambiar de sustancia

U=@(T) 1./(exp(constantes(indice)*cte./T)-1)+1/2;
fplot(U,[0,6000])
grid on
xlabel('T')
ylabel('U/(Nhw_0)')
title('Energía interna')

Cuando las temperaturas son bajas casi todos los osciladores están en el estado fundamental. Cuando las temperaturas son altas la energía interna U crece linealmente con la temperatura T

Se define la capacidad calorífica

${\displaystyle C_v=\frac{dU}{dT}=Nk{\left(\frac{\frac{\hslash {\omega }_0}{2kT}}{\sinh \left(\frac{\hslash {\omega }_0}{2kT}\right)}\right)}^2}$

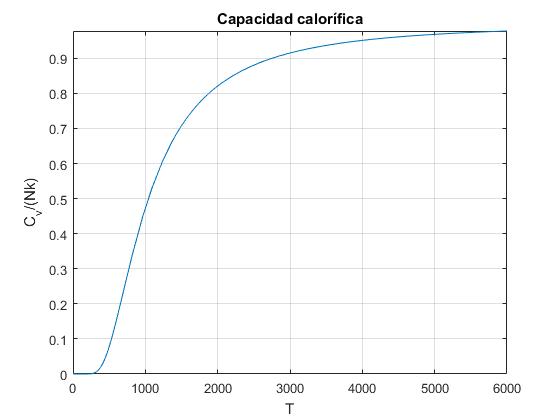
Representamos C_v/(Nk) en función de la temperatura T

cte=1.6e-19/1.3805e-23; %eV/k
%['Anhídrido carbónico (CO)', 'Hidrógeno (H2)', 'Oxígeno (O2)',
 'Nitrógeno (N2)', 'Cloro (Cl2)', 'Acido clorhídrico (ClH)'];  
constantes=[0.268, 0.543, 0.194, 0.292, 0.0698, 0.369];
indice=1; %cambiar de sustancia

Cv=@(T) (constantes(indice)*cte./(sinh(constantes(indice)*cte./(2*T)).*2*T)).^2;
fplot(Cv,[0,6000])
grid on
xlabel('T')
ylabel('C_v/(Nk)')
title('Capacidad calorífica')

Teniendo en cuenta que

${\displaystyle \sinh (x)\approx \{\begin{array}{l}xx<<1\\ e^x/2x>>1\end{array}}$

los valores límites para la capacidad calorífica, para temperaturas bajas y altas son, respectivamente

${\displaystyle C_v\approx \{\begin{array}{l}Nk{\left(\frac{\hslash {\omega }_0}{kT}\right)}^2\exp \left(\frac{\hslash {\omega }_0}{kT}\right)kT<<\hslash {\omega }_0\\ NkkT>>\hslash {\omega }_0\end{array}}$