Materiales paramagnéticos

Las propiedades magnéticas no están limitadas únicamente a las sustancias ferromagnéticas, las presentan todas las sustancias, aunque en mucho menor escala. En esta categoría, entran dos tipos de sustancias: las paramagnéticas y las diamagnéticas.

Una muestra de sustancia paramagnética situada en un campo magnético es atraída hacia la región donde el campo es más intenso, al contrario de lo que le ocurre a una sustancia diamagnética que es atraída hacia la región donde el campo es más débil.

El paramagnetismo se produce cuando las moléculas de una sustancia tienen un momento magnético permanente. El campo magnético externo produce un momento que tiende a alinear los dipolos magnéticos en la dirección del campo. La agitación térmica aumenta con la temperatura y tiende a compensar el alineamiento del campo magnético. En las sustancias paramagnéticas la susceptibilidad magnética es muy pequeña comparada con la unidad.

En el programa interactivo de esta página, experimentaremos con un modelo de sustancia paramagnética consistente en un número pequeño, pero suficiente de iones. Distinguiremos entre el comportamiento individual de cada ión y el comportamiento de la muestra en su conjunto.

Un átomo o un ión de momento magnético $\vec{μ}$ en un campo magnético $\vec{B}$ tiene una energía $U = - \vec{μ} \cdot \vec{B}$ . El momento magnético es proporcional al momento angular $\vec{μ} = g μ_{B} \vec{S}$ . Donde μ_B=9.2732·10^-24 J/T es el magnetón de Bohr y g es un factor del orden de dos.

Si $\vec{B}$ apunta en la dirección del eje Z, la energía del dipolo vale

$U = - \vec{μ} \cdot \vec{B} = - μ_{z} B = - g μ_{B} S_{z} B$

En la descripción mecánico-cuántica los valores de m=S_z son discretos y van desde -S a +S, en total 2S+1 valores. Por tanto, las componentes del momento magnético a lo largo de la dirección del campo tienen 2S+1 valores.

Ión	Momento angular S
Gd(3+)	7/2
Fe(3+)	5/2
Cr(3+)	3/2
Co(3+)	1/2

Utilizando la imagen de la descripción clásica, esta restricción nos viene a decir que no todas las orientaciones del momento magnético son posibles.

Tenemos un sistema de iones paramagnéticos a una temperatura T, que pueden ocupar 2S+1 niveles de energía. La estadística clásica nos dice que la probabilidad de que una partícula ocupe un nivel de energía U es proporcional a exp(-U/kT).

El valor medio de la componente del momento magnético a lo largo de la dirección del campo vale.

$< μ_{z} > = \frac{\sum_{m = - S}^{S} μ_{z} \exp (- U / k T)}{\sum_{m = - S}^{S} \exp (- U / k T)} = g μ_{B} \frac{\sum_{m = - S}^{S} m \exp (m u)}{\sum_{m = - S}^{S} \exp (m u)} u = \frac{g μ_{B} B}{k T}$

donde la suma se extiende a los 2S+1 posibles valores de S_z.

$< μ_{z} > = g μ_{B} \frac{1}{Z} \frac{d Z}{d u} = g μ_{B} \frac{d \ln Z}{d u} Z = \sum_{m = - S}^{S} \exp (m u)$

Z es la suma de 2S+1 términos de una progresión geométrica cuyo primer término es exp(-S·u) y cuyo último término es exp(S·u) y cuya razón es r= exp(u). Véase el ejemplo más abajo para S=3/2

$\begin{array}{l} Z = \frac{\exp (- S \cdot u) - \exp ((S + 1) u)}{1 - \exp (u)} = \frac{\exp (- (S + \frac{1}{2}) \cdot u) - \exp ((S + \frac{1}{2}) u)}{\exp (- \frac{1}{2} u) - \exp (\frac{1}{2} u)} = \frac{sinh ((S + \frac{1}{2}) \cdot u)}{sinh (\frac{1}{2} u)} \\ < μ_{z} > = g μ_{B} \frac{d}{d u} (\ln (sinh ((S + \frac{1}{2}) u) - \ln \sinh (\frac{1}{2} u)) = g μ_{B} (\frac{(S + \frac{1}{2}) \cosh ((S + \frac{1}{2}) u)}{sinh ((S + \frac{1}{2}) u)} - \frac{\frac{1}{2} \cosh (\frac{1}{2} u)}{sinh (\frac{1}{2} u)}) \\ < μ_{z} > = g μ_{B} ((S + \frac{1}{2}) \coth ((S + \frac{1}{2}) u) - \frac{1}{2} \coth (\frac{1}{2} u)) \end{array}$

Casos particulares:

Teniendo en cuenta las aproximaciones de

$\coth x = \frac{e^{x} + e^{- x}}{e^{x} - e^{- x}}$

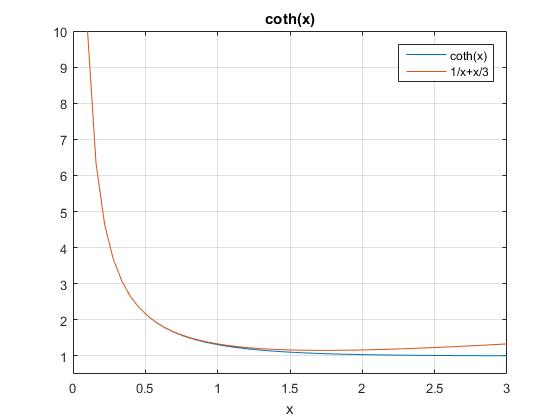
x=linspace(0.1,3,50);
y=1./tanh(x); %cotangente hiperbólica
y1=1./x+x/3;  %aproximación
plot(x,y,x,y1)
grid on
ylim([0.5,10])
legend('coth(x)','1/x+x/3')
xlabel('x')
title('coth(x)')

cuando x>>1, e^x>>e^-x por lo que cothx→1
cuando x<<1 se desarrolla en serie e^x y e^-x

$\coth x \approx \frac{1}{x} + \frac{x}{3}$

Cuando u<<1 el valor medio de la componente del momento magnético a lo largo del campo se puede aproximar a

$< μ_{z} > = \frac{g^{2} μ_{B}^{2} S (S + 1) B}{3 k T}$

que es una función lineal del cociente campo/temperatura, a esta fórmula se le conoce como ley de Curie.

Cuando u>>1, es decir, para grandes valores del campo o bajas temperaturas

<μ_z>=gμ_BS

la mayor parte de los momentos magnéticos están orientados según el campo, el valor medio de la componente del momento magnético tiende hacia un valor constante que es su valor máximo.

Actividades

Se elige el material paramagnético en el control titulado Iones.

Se introduce

la intensidad del campo magnético en Tesla, en el control titulado Campo magnético.
la temperatura en kelvin, en el control titulado Temperatura.

Se pulsa el botón titulado Nuevo

Se representa el estado de cada ión mediante un número que indica su momento magnético en unidades de Bohr, en color azul sobre fondo amarillo, cuando el vector momento magnético apunta en el sentido del campo y en color inverso cuando apunta en sentido contrario al campo aplicado. El programa calcula el momento magnético medio en unidades del magnetón de Bohr de los iones, y lo muestra en el control del mismo nombre situado bajo los controles.

Se repite varias veces la experiencia, observando el comportamiento de cada una de los iones y de la muestra en su conjunto (el momento magnético medio) modificando solamente la temperatura, pero sin cambiar el valor del campo magnético ni la sustancia paramagnética.

Comprobar que se obtienen valores parecidos del momento magnético medio para valores iguales del cociente campo/temperatura. Por ejemplo, se obtienen valores parecidos introduciendo un campo de 1 y una temperatura de 1, que introduciendo un campo de 2 y una temperatura de 2.

Introduciendo valores iguales del cociente campo/temperatura, observaremos que no podemos predecir de antemano la orientación de ión individual, sin embargo, el comportamiento del conjunto está determinado.

Comprobar, que cuando la intensidad del campo magnético es grande y la temperatura es próxima a cero, casi todos los iones están orientadas en la dirección del campo, obteniéndose el valor máximo de la componente Z del momento magnético de la sustancia.

Comprobar, que cuando la intensidad del campo magnético es pequeña y la temperatura es grande, se obtiene el valor mínimo del momento magnético medio de la sustancia, un valor próximo a cero. Hay tantos iones orientados en el sentido del campo como en sentido contrario.

Ejemplo:

Calcular el momento magnético medio <μ_z> de una muestra de iones Cr(3+) cuyo momento angular S=3/2, cuando la muestra está bajo la acción de un campo magnético de B=1.0 T, y a una temperatura de T=10 K. Datos: constante de Boltzmann k=1.3805·10^-23 J/K, magnetón de Bohr μ_B=9.2732·10^-24 J/T

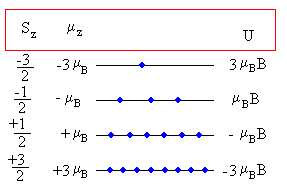
En la figura, se muestra los niveles de energía accesibles a los iones cuyo momento angular S=3/2. La energía de los niveles se indica en la columna de la derecha, y la componente del momento magnético μ_z de los iones que ocupan un nivel determinado, se indica en la columna izquierda. Se ha tomado el factor g=2.

$\begin{array}{l} u = \frac{g μ_{B} B}{k T} = 0.1344 \\ < μ_{z} > = 2 μ_{B} \frac{- \frac{3}{2} \cdot \exp (- \frac{3}{2} u) - \frac{1}{2} \exp (- \frac{1}{2} u) + \frac{1}{2} \exp (\frac{1}{2} u) + \frac{3}{2} \cdot \exp (\frac{3}{2} u)}{\exp (- \frac{3}{2} \cdot u) + \exp (- \frac{1}{2} u) + \exp (\frac{1}{2} u) + \exp (\frac{3}{2} u)} = 0.334 μ_{B} \end{array}$

Este es el momento magnético medio de la muestra en unidades del magnetón de Bohr μ_B

También podemos calcularlo por la fórmula simplificada final

$< μ_{z} > = 2 μ_{B} ((\frac{3}{2} + \frac{1}{2}) \coth ((\frac{3}{2} + \frac{1}{2}) 0.1344) - \frac{1}{2} coth (\frac{1}{2} 0.1344)) = 0.334 μ_{B}$

Iones: Temperatura (K):
Campo magnético (T):

Momento magnético medio (u. Bohr):

Referencias

Reif F. Fundamentos de Física Estadística y Térmica. Ediciones del Castillo (1968), págs. 261-264.