Dieléctricos polares
Existen dos tipos de moléculas las moléculas polares y las moléculas no polares. Las moléculas polares son aquellas en las que no coincide el centro de distribución de cargas positivas y el de las negativas, el ejemplo más significativo es el agua. Los iones hidrógeno no están alineados y dispuestos simétricamente a uno y otro lado del ión oxígeno, sino que tienen una disposición triangular.
Las moléculas no polares son aquellas en las que coincide el centro de distribución de las cargas positivas y negativas. Las moléculas de oxígeno, nitrógeno, compuestas por dos átomos iguales pertenecen a esta categoría.
Las moléculas polares bajo la acción de un campo eléctrico experimentan un par de fuerzas que tienden a orientarlas en el sentido del campo. Las moléculas no polares, se hacen polares en presencia de un campo eléctrico, ya que las fuerzas sobre cada tipo de carga son iguales y de sentido contrario.
Un dipolo eléctrico es un sistema formado por dos cargas iguales q y de signo contrario, separadas una distancia d. Se define el momento dipolar p, como un vector cuyo módulo es el producto de la carga q por la separación entre cargas d, de dirección la recta que las une, y de sentido de la negativa a la positiva.
Los momentos dipolares de algunas moléculas se recogen en la siguiente tabla:
| Moléculas | Momento dipolar ·10-30 C·m |
|---|---|
| Agua | 6.2 |
| Nitrobenceno | 13.2 |
| Fenol | 5.2 |
| Clorhídrico | 3.5 |
| Bromhídrico | 2.6 |
| Iodhídrico | 1.3 |
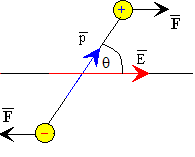
Sobre un dipolo situado en un campo eléctrico actúa un par fuerzas cuyo momento tiende a orientar al dipolo en la dirección del campo. Sin embargo, esta tendencia está contrarrestada por la agitación térmica de las moléculas. Para cada campo y cada temperatura, tendremos una orientación media resultado del compromiso entre ambas tendencias contrapuestas.
La energía de un dipolo en un campo eléctrico local es .
Nota: El campo local que afecta a una molécula y el campo macroscópico son diferentes. La relación entre ambos se detalla en la segunda refrencia
La polarización de la sustancia es P=Np<cosθ>, donde N es el número de moléculas por unidad de volumen y p<cosθ> es el valor medio de la componente del momento dipolar en la dirección del campo. De acuerdo con la fórmula de la estadística clásica
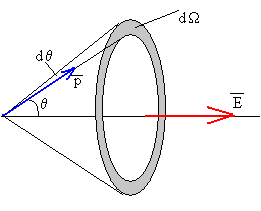
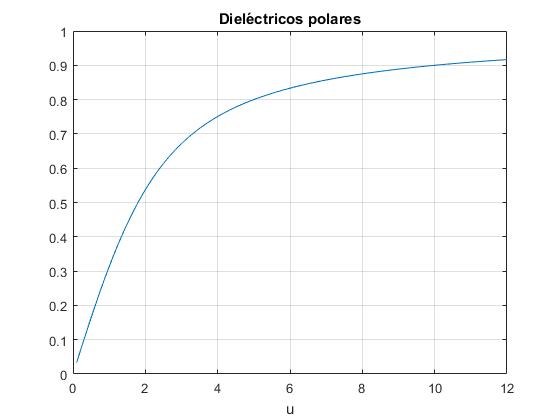
donde exp(-U/kT) es la probabilidad de que un dipolo esté orientado según un ángulo sólido comprendido entre Ω y Ω+dΩ. El área sombreada de la figura, es dΩ=2π·sinθ·dθ. La integración conduce a la siguiente función conocida como ley de Langevin
Casos particulares:
- Cuando u<<1 la polarización P se puede aproximar a la función
- Cuando u>>1, es decir, para grandes valores del campo o bajas temperaturas,
La polarización es una función lineal del cociente campo/temperatura. Esta fórmula es análoga a la ley de Curie para los materiales paramagnéticos
P=Np
P tiende hacia un valor constante que es su valor máximo.
u=0.1:0.1:12;
y=1./tanh(u)-1./u;
plot(u,y)
grid on
xlabel('u')
title('Dieléctricos polares')
Actividades
Se selecciona el tipo de moléculas polares en el control titulado Moléculas.
Se introduce
- la intensidad del campo eléctrico (en unidades 107 N/C), en el control titulado Campo eléctrico.
- la temperatura en kelvin, en el control titulado Temperatura.
Se pulsa el botón titulado Nuevo
Se muestra el estado de cada molécula representada por una flecha: en color azul, aquellas cuyo momento dipolar está orientadas en el sentido del campo y en color rojo, las que están orientadas en sentido contrario al campo. El programa calcula la polarización P/N de la sustancia en unidades 10-30 C·m y la muestra en la parte superior derecha
Se repite varias veces la experiencia, observando el comportamiento de cada una de las moléculas del dieléctrico y del dieléctrico en su conjunto (la polarización) modificando solamente la temperatura, pero sin cambiar el valor del campo eléctrico, ni la sustancia dieléctrica.
Comprobamos que se obtienen valores parecidos de la polarización para valores iguales del cociente campo temperatura. Por ejemplo, se obtienen valores parecidos introduciendo un campo de 10 y una temperatura de 100, que introduciendo un campo de 20 y una temperatura de 200. Introduciendo valores iguales del cociente campo/temperatura, observaremos que no podemos saber de antemano la orientación de una molécula individual, sin embargo, el comportamiento del conjunto está determinado por la ley de Langevin.
Comprobamos, que cuando la intensidad del campo eléctrico es grande y la temperatura es próxima a cero, casi todas las moléculas están orientadas en la dirección del campo, obteniéndose el valor máximo de la polarización de la sustancia dieléctrica.
Comprobamos, que cuando la intensidad del campo eléctrico es pequeña y la temperatura es grande, la orientación de los momentos dipolares es al azar, obteniéndose el valor mínimo de la polarización, un valor próximo a cero.
Ejemplo:
Calcular la polarización media (P/N) de la molécula de agua (p=6.2·10-30 C·m) cuando una muestra de este líquido está bajo la acción de un campo eléctrico E=10·107 N/C y a una temperatura de T=293 K. La constante de Boltzmann vale k=1.3805·10-23 J/K
Referencias
Alonso M., Finn E.. Física, Fundamentos Cuánticos y Estadísticos. Fondo Educativo Interamericano (1971). Ejemplo 10.5, págs 459-460
Loarrain Paul, Corson Dale R. Campos y Ondas electromagnéticos. Selecciones Científicas pág. 108-128

