Potencial periódico

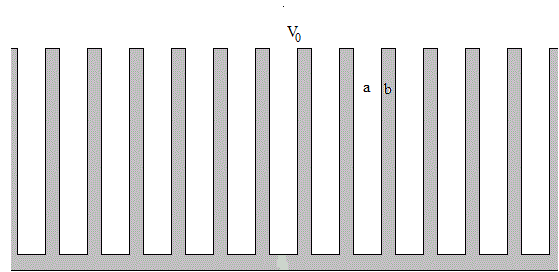
Consideremos el movimiento de una partícula en un potencial periódico de periodo l=a+b, formado por pozos de potencial de anchura a y profundidad V₀ y barreras de potencial de anchura b.

La función de onda tiene la forma

$Ψ (x) = u (x) \exp (i K x)$

Obtenemos la imagen de las funciones de onda considerando que u(x) se asemeja a la función de onda de los átomos aislados (de un pozo de potencial)

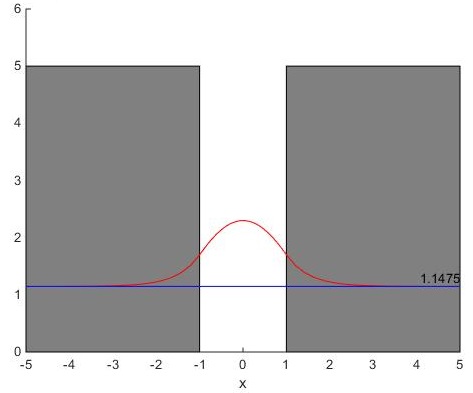
y reemplazando exp(iKx) por las funciones de onda de una partícula libre en una pozo infinito de potencial. Esto es lo que hemos observado al visualizar las funciones de onda de los primeros niveles de energía de un sistema de pozos de potencial.

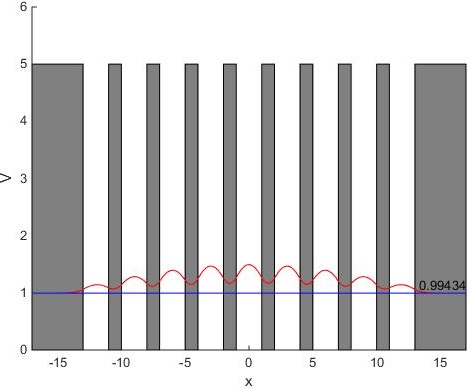
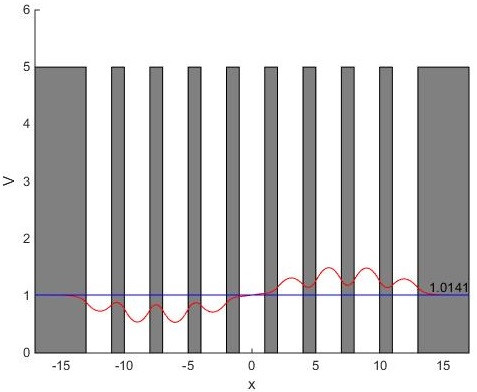
Como el potencial es periódico con periodo l=a+b, suma de la anchura a del pozo y de la separación b entre pozos, se deberá cumplir que

u(x+l)=u(x)

Ambas expresiones constituyen el teorema de Bloch. De ambas, se deduce que

$ψ (x + l) = u (x + l) \exp (i K (x + l)) = u (x) \exp (i K x) \exp (i K l) = ψ (x) \exp (i K l)$

Sistema de pozos de potencial

En la página previa titulada Sistema de pozos de potencial, calculamos los niveles de energía y representamos las funciones de onda de un sistema de N pozos de potencial. En esta página, se estudia el caso en el que N es infinito

En la figura, se muestra las regiones I y II en las que vamos a obtener la solución de la ecuación de Schrödinger.

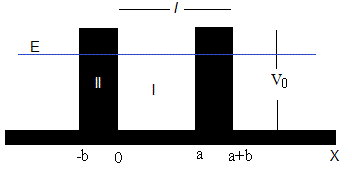
$- \frac{ℏ^{2}}{2 m} \frac{d^{2} ψ (x)}{d x^{2}} + V (x) \cdot ψ (x) = E \cdot ψ (x)$

En la primera, 0≤x<a

$\begin{array}{l} V (x) = 0 \\ ψ_{I} (x) = A \exp (i k x) + B \exp (- i k x), k^{2} = \frac{2 m}{ℏ^{2}} E \end{array}$

En la segunda región, -b≤x<0

$\begin{array}{l} V (x) = V_{0} \\ ψ_{I I} (x) = C \exp (q x) + D \exp (- q x), q^{2} = \frac{2 m}{ℏ^{2}} (V_{0} - E) \end{array}$

Escribiremos ahora las condiciones de continuidad de la función de onda y de su derivada primera en los puntos x=0, y x=a.

en x=0

$\begin{array}{l} ψ_{I} (0) = ψ_{I I} (0), {\frac{d ψ_{I} (x)}{d x} |}_{x = 0} = {\frac{d ψ_{I I} (x)}{d x} |}_{x = 0} \\ {\begin{cases} A + B = C + D \\ i k (A - B) = q (C - D) \end{cases} \end{array}$

en x=a, por el teorema de Bloch

$\begin{array}{l} ψ (x + a + b) = ψ (x) \exp (i K (a + b)) \\ ψ (a) = ψ (- b) \exp (i K (a + b)) \\ ψ_{I} (a) = ψ_{I I} (- b) \exp (i K (a + b)) \\ A \exp (i k a) + B \exp (- i k a) = (C \exp (- q b) + D \exp (q b)) \exp (i K (a + b)) \\ {\frac{d ψ_{I} (x)}{d x} |}_{x = a} = {\frac{d ψ_{I I} (x)}{d x} |}_{x = - b} \exp (i K (a + b)) \\ i k (A \exp (i k a) - B \exp (- i k a)) = q (C \exp (- q b) - D \exp (q b)) \exp (i K (a + b)) \end{array}$

Tenemos un sistema homogéneo de cuatro ecuaciones con cuatro incógnitas, el determinante de los coeficientes debe ser cero.

${\begin{cases} A + B - C - D = 0 \\ A \cdot i k - B \cdot i k - C \cdot q + D \cdot q = 0 \\ A \cdot e^{i k a} + B \cdot e^{- i k a} - C \cdot e^{- q b} e^{i K (a + b)} - D \cdot e^{q b} e^{i K (a + b)} = 0 \\ A \cdot i k e^{i k a} - i k B e^{- i k a} - C \cdot q e^{- q b} e^{i K (a + b)} + D \cdot q e^{q b} e^{i K (a + b)} = 0 \end{cases}$

Despejamos C y D en las dos primeras ecuaciones y en las dos últimas

$\begin{array}{l} 2 C = (1 + \frac{i k}{q}) A + (1 - \frac{i k}{q}) B, 2 D = (1 - \frac{i k}{q}) A + (1 + \frac{i k}{q}) B \\ 2 e^{- q b} C = e^{- i K (a + b)} ((1 + \frac{i k}{q}) e^{i k a} A + (1 - \frac{i k}{q}) e^{- i k a} B) \\ 2 e^{q b} D = e^{- i K (a + b)} ((1 - \frac{i k}{q}) e^{i k a} A + (1 + \frac{i k}{q}) e^{- i k a} B) \end{array}$

Obtenemos un sistema homogéneo de dos ecuaciones con dos incógnitas A y B

${\begin{cases} (1 + \frac{i k}{q}) (\exp (q b - i K (a + b) + i k a) - 1) A + (1 - \frac{i k}{q}) (\exp (q b - i K (a + b) - i k a) - 1) B = 0 \\ (1 - \frac{i k}{q}) (\exp (- q b - i K (a + b) + i k a) - 1) A + (1 + \frac{i k}{q}) (\exp (- q b - i K (a + b) - i k a) - 1) B = 0 \end{cases}$

El determinante ha de ser cero

$\begin{array}{l} {(1 + \frac{i k}{q})}^{2} (\exp (q b - i K (a + b) + i k a) - 1) (\exp (- q b - i K (a + b) - i k a) - 1) \\ - {(1 - \frac{i k}{q})}^{2} (\exp (q b - i K (a + b) - i k a) - 1) (\exp (- q b - i K (a + b) + i k a) - 1) = 0 \end{array}$

Realizando operaciones

$\begin{array}{l} (1 - \frac{k^{2}}{q^{2}}) {\exp (q b - i K (a + b)) (- 2 i \sin (k a)) + \exp (- q b - i K (a + b)) (2 i \sin (k a))} + \\ (\frac{2 i k}{q}) {2 \exp (- i 2 K (a + b)) - \exp (q b - i K (a + b)) (2 \cos (k a)) - \exp (- q b - i K (a + b)) (2 \cos (k a)) + 2} = 0 \end{array}$

Obtenemos la expresión

$\begin{array}{l} (1 - \frac{k^{2}}{q^{2}}) {- 2 i \exp (- i K (a + b)) \sin (k a) \sinh (q b)} + \\ (\frac{2 i k}{q}) {\exp (- 2 i K (a + b)) - 2 \exp (- i K (a + b)) \cos (k a) \cosh (q b) + 1} = 0 \end{array}$

Las partes real e imaginaria de esta expresión son

$\begin{array}{l} \sin (K (a + b)) {- (1 - \frac{k^{2}}{q^{2}}) \sin (k a) \sinh (q b) + \frac{2 k}{q} (\cos (K (a + b)) - \cos (k a) \cosh (q b))} = 0 \\ \cos (K (a + b)) {- (1 - \frac{k^{2}}{q^{2}}) \sin (k a) \sinh (q b) + \frac{2 k}{q} (\cos (K (a + b)) - \cos (k a) \cosh (q b))} = 0 \end{array}$

El resultado es

$\frac{q^{2} - k^{2}}{2 k q} \sin (k a) \sinh (q b) + \cos (k a) \cosh (q b) = \cos (K (a + b))$

Ya que el valor absoluto del coseno no puede ser mayor que la unidad, obtenemos así la condición impuesta a k y a q y por tanto, a la energía E.

$- 1 \leq \frac{q^{2} - k^{2}}{2 k q} \sin (k a) \sinh (q b) + \cos (k a) \cosh (q b) \leq 1$

Esta condición define las bandas de energía permitidas.

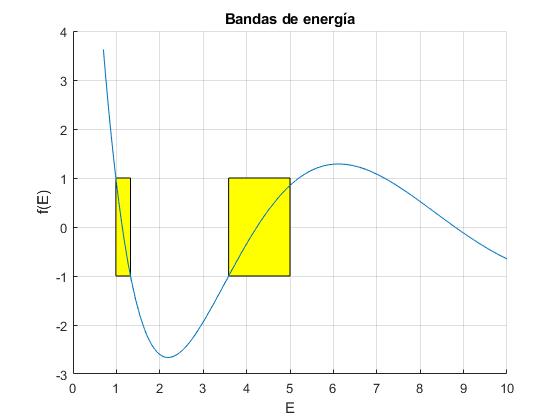
Representamos la función f(E) para a=2, b=1 y V₀=5

$\begin{array}{l} f (E) = \frac{q^{2} - k^{2}}{2 k q} \sin (k a) \sinh (q b) + \cos (k a) \cosh (q b) \\ q = \sqrt{V_{0} - E}, k = \sqrt{E} \end{array}$

Calculamos las raíces de las ecuaciones transcendentes, f(E)-1=0 y f(E)+1=0, señalamos las regiones (bandas de energía) en la que se cumple que -1≤f(E)≤+1

function pozos
    a=2;  %anchura del pozo
    b=1; %separación entre pozos
    H=5; %profundidad del pozo
    ff=@(x) bandas(x)+1; 
    xb=buscar_intervalos(ff,0.1,H-0.1,20);
    nb=size(xb);
    E1=zeros(1,nb(1));
    for m=1:nb(1)
        E1(m)=fzero(ff,[xb(m,1) xb(m,2)]);
    end
    ff=@(x)bandas(x)-1; 
    xb=buscar_intervalos(ff,0.1,H-0.1,20);
    nb=size(xb);
    E2=zeros(1,nb(1));
    for m=1:nb(1)
        E2(m)=fzero(ff,[xb(m,1) xb(m,2)]);
    end
    E2=[E2,5];
    disp(E1)
    disp(E2)
    hold on
    for i=1:length(E1)
        XX=[E1(i), E1(i), E2(i), E2(i)];
        YY=[-1,1,1,-1];
        fill(XX,YY,'yellow')
    end
    fplot(@(x) bandas(x), [0.7,10])
    hold off
    grid on
    xlabel('E');
    ylabel('f(E)')
    title('Bandas de energía')
    
    function res=bandas(E)
        k=sqrt(E);
        q=sqrt(H-E);
        res=cos(k*a).*cosh(q*b)+(q.^2-k.^2).*sin(k*a).*sinh(q*b)./(2*q.*k);
    end

   function xb = buscar_intervalos(f,a,b,n)
        x = a:(b-a)/n:b;
        j = 0; 
        y1=f(x(1));
        xb=[];
        for i = 1:length(x)-1
            y2=f(x(i+1));
            if sign(y1) ~= sign(y2) 
                j = j + 1;
                xb(j,1) = x(i);
                xb(j,2) = x(i+1);
            end
            y1=y2;
        end
        if isempty(xb) 
            disp('no se han encontrado cambios de signo')
        else
            disp(['número de intervalos:' int2str(j)]) 
        end
    end
end

    1.3246    3.5864
    0.9876    5.0000

Cálculo de las bandas de energía

function res =kp(a, b, H, cte, E)  
   k=sqrt(E);
   q=sqrt(H-E);
   res=cos(k*a)*cosh(q*b)+(q^2-k^2)/(2*q*k)*sin(k*a)*sinh(q*b)+cte;
end

a=2;  %anchura del pozo
b=1; %separación entre pozos
H=5.0; %profundidad del pozo

f=@(E) kp(a,b,H, -1.0, E);
xb=buscar_intervalos(f,0.1,H-0.1,10);
nb=size(xb);
for i=1:nb(1)
    bandas(i)=fzero(f,[xb(i,1) xb(i,2)]);
end

f=@(E) kp(a,b,H, 1.0, E);
xb=buscar_intervalos(f,0.1,H-0.1,10);
nc=size(xb);
for i=1:nc(1)
    bandas(i+nb(1))=fzero(f,[xb(i,1) xb(i,2)]);
end
bandas=sort(bandas);  %ordena de menor a mayor
if rem(length(bandas),2)==1
    bandas=[bandas H];
end
hold on
%representa las bandas de energía mediante rectángulos de color azul
for j=1:2:length(bandas)
    xx=[3 3 4 4];
    yy=[bandas(j), bandas(j+1), bandas(j+1), bandas(j)];
    fill(xx,yy,'b')
    text(4, bandas(j),num2str(bandas(j)),
'VerticalAlignment','top', 'HorizontalAlignment','right');
    text(4, bandas(j+1),num2str(bandas(j+1)),
'VerticalAlignment','bottom', 'HorizontalAlignment','right');
end
.....

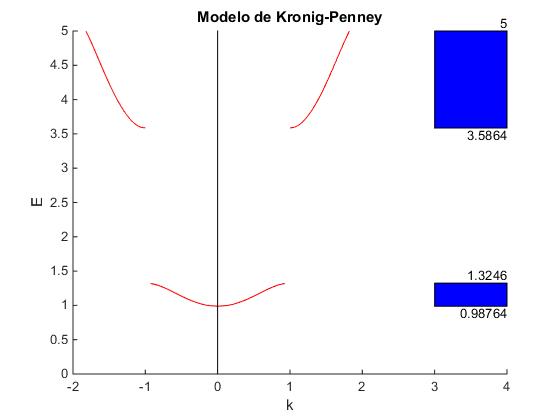
La función buscar_intervalos busca los intervalos donde la función f(E) cambia de signo. Se ha definido en la página Atomo, molécula... sólido lineal

Zonas de Brillouin

Puede observarse que la energía presenta una discontinuidad, para números de onda k múltiplos de π/l, donde l=a+b es el periodo de la red lineal. Estos valores representan fronteras entre zonas de Brillouin contiguas. Los intervalos de existencia de cada una de las zonas medidas en el eje vertical representan las bandas de energía, que se muestran como rectángulos de color azul en la parte derecha de la figura.

Completamos el código del script para representar las zonas de Brillouin

....
f=@(E) kp(a,b,H, 0.0, E);

for j=1:2:length(bandas)
    E=bandas(j):0.01:bandas(j+1);
    k=zeros(length(E));
    k(1)=(j-1)/2;
    for i=2:length(E)          
        y=f(E(i));
        if(abs(y)<1)
            angulo=acos(y);
            if rem((j-1)/2,2)==1
                k(i)=(j-1)/2+1-angulo/pi;
            else
                k(i)=(j-1)/2+angulo/pi;
            end
        end
    end
    plot(k,E,'r') %simetría
    plot(-k,E,'r')
end
line([0,0],[0,H],'color','k')

hold off
xlabel('k')
ylabel('E')
title('Modelo de Kronig-Penney')

Aproximación, potenciales delta de Dirac

Partimos de la ecuación

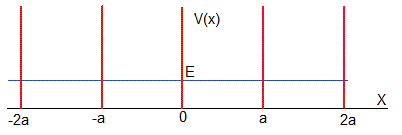
$\frac{q^{2} - k^{2}}{2 k q} \sin (k a) \sinh (q b) + \cos (k a) \cosh (q b) = \cos (K (a + b))$

Consideremos el caso en el que b→0 y V₀→∞

cos(K(a+b))→cos(Ka)

q>>k

$\begin{array}{l} \frac{q^{2} - k^{2}}{2 q k} \to \frac{q}{2 k} \\ q b = \sqrt{\frac{2 m}{ℏ^{2}} (V_{0} - E)} \approx \sqrt{\frac{2 m}{ℏ^{2}} (V_{0} b) b} \\ \sinh (q b) \approx q b \\ \cosh (q b) \approx 1 \end{array}$

V₀b es el producto de una cantidad grande por una cantidad pequeña, un número finito. qb es una cantidad pequeña. El resultado es

$\begin{array}{l} \cos (K a) = \cos (k a) + \frac{q^{2} b}{2 k} \sin (k a) \\ \cos (K a) = \cos (k a) + \frac{p}{k a} \sin (k a), p = \frac{q^{2} b a}{2} \end{array}$

donde p es un parámetro

Sistema de potenciales delta de Dirac

Vamos a obtener un resultado similar analizando un sistema de infinitos potenciales delta de Dirac

$V (x) = - α \frac{ℏ^{2}}{2 m} \sum_{- \infty}^{\infty} δ (x - n a)$

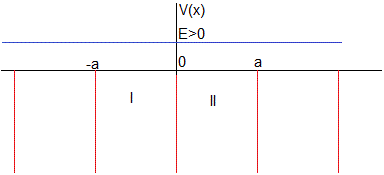
Estudiaremos por separado los dos posibles casos

Energías positivas, E>0
Energías negativas, E<0

Sea E>0

En la primera, -a≤x<0

$\begin{array}{l} V (x) = 0 \\ ψ_{I} (x) = A \exp (i k x) + B \exp (- i k x), k^{2} = \frac{2 m}{ℏ^{2}} E \end{array}$

En la segunda región, 0≤x<a

$\begin{array}{l} V (x) = 0 \\ ψ_{I I} (x) = C \exp (i k x) + D \exp (- i k x) \end{array}$

El teorema de Bloch establece

$ψ (x) = ψ (x - a) \exp (i K a)$

Lo que implica que, cualquiera que sea el valor de x

$\begin{array}{l} ψ_{I I} (x) = ψ_{I} (x - a) \exp (i K a) \\ C \exp (i k x) + D \exp (- i k x) = (A \exp (i k (x - a)) + B \exp (- i k (x - a))) \exp (i K a) \\ C \exp (i k x) + D \exp (- i k x) = A \exp (i k x) \exp (i (K - k) a) + B \exp (- i k x) \exp (i (K + k) a) \\ {\begin{cases} C = A \exp (i (K - k) a) \\ D = B \exp (i (K + k) a) \end{cases} \end{array}$

Las funciones de onda en las dos regiones I y II son

$\begin{array}{l} ψ_{I} (x) = A \exp (i k x) + B \exp (- i k x), - a < x < 0 \\ ψ_{I I} (x) = A \exp (i (K - k) a) \exp (i k x) + B \exp (i (K + k) a) \exp (- i k x), 0 < x < a \end{array}$

La función de onda es continua en x=0

$\begin{array}{l} ψ_{I} (0) = ψ_{I I} (0) \\ A + B = A \exp (i (K - k) a) + B \exp (i (K + k) a) \end{array}$

La derivada primera de la función de onda no es continua en x=0

$\begin{array}{l} - \frac{ℏ^{2}}{2 m} \int_{- ε}^{+ ε} \frac{d^{2} ψ (x)}{d x^{2}} d x - \int_{- ε}^{+ ε} α \frac{ℏ^{2}}{2 m} δ (x) \cdot ψ (x) \cdot d x = E \cdot \int_{- ε}^{+ ε} ψ (x) \cdot d x \\ - \frac{ℏ^{2}}{2 m} \lim_{ε \to 0} ({\frac{d ψ_{I I} (x)}{d x} |}_{+ ε} - {\frac{d ψ_{I} (x)}{d x} |}_{- ε}) - α \frac{ℏ^{2}}{2 m} ψ_{I} (0) = 0 \\ \lim_{ε \to 0} ({i k A \exp (- i k x) \exp (i (K - k) a) - i k B \exp (i k x) \exp (i (K + k) a) |}_{+ ε} {- (i k A \exp (- i k x) - i k B \exp (i k x)) |}_{- ε}) + α (A + B) = 0 \\ \lim_{ε \to 0} ({i k A \exp (- i k ε) \exp (i (K - k) a) - i k B \exp (i k ε) \exp (i (K + k) a) |}_{+ ε} {- (i k A \exp (i k ε) - i k B \exp (- i k ε)) |}_{- ε}) + α (A + B) = 0 \\ (i k A \exp (i (K - k) a) - i k B \exp (i (K + k) a)) - (i k A - i k B) + α (A + B) = 0 \end{array}$

Resolvemos el sistema homogéneo de dos ecuaciones con dos incógnitas A y B

${\begin{cases} A (e^{i (K - k) a} - 1) + B (e^{i (K + k) a} - 1) = 0 \\ A (e^{i (K - k) a} - 1 + \frac{α}{i k}) + B (- e^{i (K + k) a} + 1 + \frac{α}{i k}) = 0 \end{cases}$

El determinante tiene que ser cero

$\begin{array}{l} (e^{i (K - k) a} - 1) (- e^{i (K + k) a} + 1 + \frac{α}{i k}) - (e^{i (K + k) a} - 1) (e^{i (K - k) a} - 1 + \frac{α}{i k}) = 0 \\ - 2 e^{2 i K a} - 2 + 2 e^{i K a} (e^{- i k a} + e^{i k a}) + \frac{α}{i k} e^{i K a} (e^{- i k a} - e^{i k a}) = 0 \end{array}$

Obtenemos la expresión

$- e^{2 i K a} - 1 + 2 e^{i K a} \cos (k a) - \frac{α}{k} e^{i K a} \sin (k a) = 0$

Las partes real e imaginaria de esta expresión son

$\begin{array}{l} \cos (K a) {2 \cos (K a) - 2 \cos (k a) + \frac{α}{k} \sin (k a)} = 0 \\ \sin (K a) {2 \cos (K a) - 2 \cos (k a) + \frac{α}{k} \sin (k a)} = 0 \end{array}$

El resultado es

$\cos (K a) = \cos (k a) - \frac{α}{2 k} \sin (k a)$

Ya que el valor absoluto del coseno no puede ser mayor que la unidad, obtenemos así la condición impuesta a k y por tanto, a la energía E.

$- 1 \leq \cos (k a) - \frac{α}{2 k} \sin (k a) \leq 1$

Representamos la función f(E) para la separación a=1, parámetro α=2

$\begin{array}{l} f (E) = \cos (k a) - \frac{α}{2 k} \sin (k a) \\ k = \sqrt{E} \end{array}$

Calculamos las raíces de las ecuaciones transcendentes, f(E)-1=0 y f(E)+1=0, señalamos las regiones (bandas de energía) en la que se cumple que -1≤f(E)≤+1

function delta_dirac_25
    a=1; 
    alfa=2; %parámetro
    
    ff=@(x) bandas(x)+1; 
    xb=buscar_intervalos(ff,0.1,37,20);
    nb=size(xb);
    E1=zeros(1,nb(1));
    for m=1:nb(1)
        E1(m)=fzero(ff,[xb(m,1) xb(m,2)]);
    end
    ff=@(x)bandas(x)-1; 
    xb=buscar_intervalos(ff,0.1,37,20);
    nb=size(xb);
    E2=zeros(1,nb(1));
    for m=1:nb(1)
        E2(m)=fzero(ff,[xb(m,1) xb(m,2)]);
    end
    E2=[0,E2];
    disp(E1)
    disp(E2)
    hold on
    for i=1:length(E1)
        XX=[E1(i), E1(i), E2(i), E2(i)];
        YY=[-1,1,1,-1];
        fill(XX,YY,'yellow')
    end
    fplot(@(x) bandas(x), [0.1,37])
    hold off
    grid on
    xlabel('E');
    ylabel('f(E)')
    title('Bandas de energía')
    
    function res=bandas(E)
        k=sqrt(E);
        res=cos(k*a)-alfa*sin(k*a)./(2*k);
    end

   function xb = buscar_intervalos(f,a,b,n)
        x = a:(b-a)/n:b;
        j = 0; 
        y1=f(x(1));
        xb=[];
        for i = 1:length(x)-1
            y2=f(x(i+1));
            if sign(y1) ~= sign(y2) 
                j = j + 1;
                xb(j,1) = x(i);
                xb(j,2) = x(i+1);
            end
            y1=y2;
        end
        if isempty(xb) 
            disp('no se han encontrado cambios de signo')
        else
            disp(['número de intervalos:' int2str(j)]) 
        end
    end
end

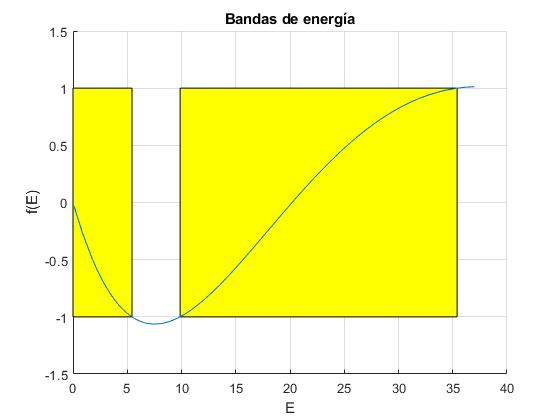
    5.4341    9.8696
         0   35.4046

Sea E<0

La solución de la ecuación de Schrödinger para E<0

$\begin{array}{l} V (x) = 0 \\ ψ_{I} (x) = A \exp (q x) + B \exp (- q x), q^{2} = - \frac{2 m}{ℏ^{2}} E \end{array}$

En la expresión del determinante, sustituimos ik por q

$- 2 e^{2 i K a} - 2 + 2 e^{i K a} (e^{- q a} + e^{q a}) + \frac{α}{q} e^{i K a} (e^{- q a} - e^{q a}) = 0$

Obtenemos la expresión

$- e^{2 i K a} - 1 + 2 e^{i K a} \cosh (q a) - \frac{α}{q} e^{i K a} \sinh (q a) = 0$

Las partes real e imaginaria de esta expresión son

$\begin{array}{l} \cos (K a) {2 \cos (K a) - 2 \cosh (q a) + \frac{α}{k} \sinh (q a)} = 0 \\ \sin (K a) {2 \cos (K a) - 2 \cosh (q a) + \frac{α}{k} \sinh (q a)} = 0 \end{array}$

El resultado es

$\cos (K a) = \cosh (q a) - \frac{α}{2 k} \sinh (q a)$

Ya que el valor absoluto del coseno no puede ser mayor que la unidad, obtenemos así la condición impuesta a q y por tanto, a la energía E.

$- 1 \leq \cosh (q a) - \frac{α}{2 k} \sinh (q a) \leq 1$

Representamos la función f(E) para la separación a=1, parámetro α=1

$\begin{array}{l} f (E) = \cosh (q a) - \frac{α}{2 k} \sinh (q a) \\ q = \sqrt{- E} \end{array}$

Calculamos las raíces de las ecuaciones transcendentes, f(E)-1=0 y f(E)+1=0, señalamos las regiones (bandas de energía) en la que se cumple que -1≤f(E)≤+1

function delta_dirac_26
    a=1; 
    alfa=2; %parámetro
    
    ff=@(x) bandas(x)+1; 
    xb=buscar_intervalos(ff,-5,0.1,20);
    nb=size(xb);
    E1=zeros(1,nb(1));
    for m=1:nb(1)
        E1(m)=fzero(ff,[xb(m,1) xb(m,2)]);
    end
    ff=@(x)bandas(x)-1; 
    xb=buscar_intervalos(ff,-5,0.1,20);
    nb=size(xb);
    E2=zeros(1,nb(1));
    for m=1:nb(1)
        E2(m)=fzero(ff,[xb(m,1) xb(m,2)]);
    end
    E1=[E1,0];
    disp(E1)
    disp(E2)
    hold on
    for i=1:length(E1)
        XX=[E1(i), E1(i), E2(i), E2(i)];
        YY=[-1,1,1,-1];
        fill(XX,YY,'yellow')
    end
    fplot(@(x) bandas(x), [-5,0.1])
    hold off
    grid on
    xlabel('E');
    ylabel('f(E)')
    title('Bandas de energía')
    
    function res=bandas(E)
        k=sqrt(-E);
        res=cosh(k*a)-alfa*sinh(k*a)./(2*k);
    end

   function xb = buscar_intervalos(f,a,b,n)
        x = a:(b-a)/n:b;
        j = 0; 
        y1=f(x(1));
        xb=[];
        for i = 1:length(x)-1
            y2=f(x(i+1));
            if sign(y1) ~= sign(y2) 
                j = j + 1;
                xb(j,1) = x(i);
                xb(j,2) = x(i+1);
            end
            y1=y2;
        end
        if isempty(xb) 
            disp('no se han encontrado cambios de signo')
        else
            disp(['número de intervalos:' int2str(j)]) 
        end
    end
end

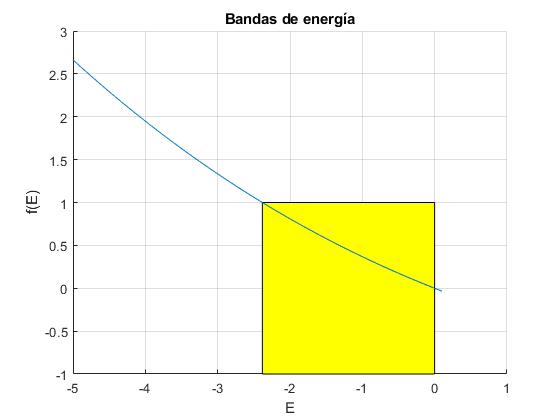
     0
   -2.3821

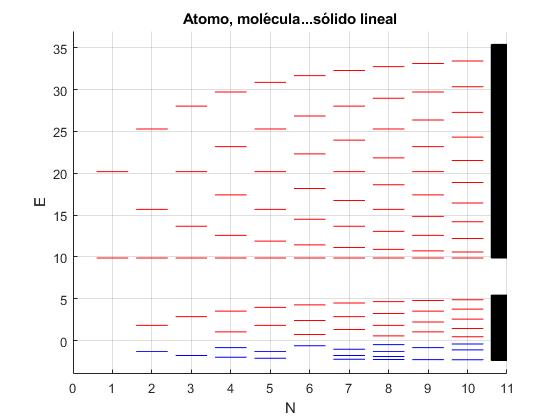
Bandas de energía

Añadimos al script al final de la página titulada Sistema de potenciales delta de Dirac el código que calcula y representa las bandas de energía (en color negro) para un sistema de infinitos potenciales delta de Dirac cuyo parámetro α=2 y separación a=1

function delta_dirac_23
    a=1;
    alfa=2; %parámetro
    for N=1:10 %número de potenciales delta
        ff=@(x) niveles_sup(x); %para E>0
        xb=buscar_intervalos(ff,0.1,14,50);
        nb=size(xb);
        ks=zeros(1,nb(1));
        for m=1:nb(1)
            ks(m)=fzero(ff,[xb(m,1) xb(m,2)]);
    	end
        ff=@(x) niveles_inf(x); %para E<0
        xb=buscar_intervalos(ff,0.1,14,50);
        nb=size(xb);
        ki=zeros(1,nb(1));
        for m=1:nb(1)
            ki(m)=fzero(ff,[xb(m,1) xb(m,2)]);
        end
        ff=@(x) bandas_inf(x); %para E>0
        xb=buscar_intervalos(ff,0,16,50);
        nb=size(xb);
        bi=zeros(1,nb(1));
        for m=1:nb(1)
            bi(m)=fzero(ff,[xb(m,1) xb(m,2)]);
        end
        ff=@(x) bandas_sup(x); %para E>0
        xb=buscar_intervalos(ff,0.1,16,50);
        nb=size(xb);
        bs=zeros(1,nb(1));
        for m=1:nb(1)
            bs(m)=fzero(ff,[xb(m,1) xb(m,2)]);
        end
        
         ff=@(x) bandas1_sup(x); %para E<0
        xb=buscar_intervalos(ff,0,5,50);
        nb=size(xb);
        b1s=zeros(1,nb(1));
        for m=1:nb(1)
            b1s(m)=fzero(ff,[xb(m,1) xb(m,2)]);
        end
         ff=@(x) bandas1_inf(x); %para E<0
        xb=buscar_intervalos(ff,0.1,5,50);
        nb=size(xb);
        b1i=zeros(1,nb(1));
        for m=1:nb(1)
            b1i(m)=fzero(ff,[xb(m,1) xb(m,2)]);
        end
        bn=sort([bi,bs]);
        hold on
%niveles
        for i=1:length(ks)  %para E>0
            line([N-0.4 N+0.4],[ks(i)^2, ks(i)^2], 'color','r')
        end
        for i=1:length(ki)  %para E<0
            line([N-0.4 N+0.4],[-ki(i)^2, -ki(i)^2], 'color','b')
        end
    end
%bandas
    for i=1:2:length(bn)-1
        XX=[N+1-0.4,N+1+0.4, N+1+0.4, N+1-0.4];
        YY=[bn(i)^2, bn(i)^2, bn(i+1)^2, bn(i+1)^2];
        fill(XX,YY,'k')
    end
        XX=[N+1-0.4,N+1+0.4, N+1+0.4, N+1-0.4];
        YY=[ -b1s(1)^2, -b1s(1)^2, -b1s(2)^2, -b1s(2)^2];
        fill(XX,YY,'k')
    hold off
    grid on
    xlim([0,11])
    %ylim([-4,37]) 
    xlabel('N');
    ylabel('E')
    title('Atomo, molécula...sólido lineal')

    function res=bandas_inf(k) %para E>0
        res=k*cos(k*a)-alfa*sin(k*a)/2+k;
    end
    function res=bandas_sup(k)
        res=k*cos(k*a)-alfa*sin(k*a)/2-k;
    end
    function res=bandas1_inf(k) %para E<0
        res=k*cosh(k*a)-alfa*sinh(k*a)/2+k;
    end
    function res=bandas1_sup(k)
        res=k*cosh(k*a)-alfa*sinh(k*a)/2-k;
    end

    function res=niveles_inf(k) %para E<0
        T=eye(2);
        for s=N:-1:1
            M=[1,1; 1-alfa/k,-1-alfa/k];  
            MI=[exp(k*a),exp(k*a);exp(-k*a),-exp(-k*a)]/2;
            T=(MI*M)*T;
        end
        res=T(1,1)+T(2,1)-(T(1,2)+T(2,2))*exp(-2*k*a);
    end

    function res=niveles_sup(k) %para E>0
        T=eye(2);
        for s=N:-1:1
            M=[0,1; 1,alfa/k];  
            MI=[sin(k*a),cos(k*a);cos(k*a),-sin(k*a)];
            T=(MI*M)*T;
        end
        res=T(2,1)*cos(k*a)-T(2,2)*sin(k*a);
    end

   function xb = buscar_intervalos(f,a,b,n)
        x = a:(b-a)/n:b;
        j = 0; 
        y1=f(x(1));
        xb=[];
        for i = 1:length(x)-1
            y2=f(x(i+1));
            if sign(y1) ~= sign(y2) 
                j = j + 1;
                xb(j,1) = x(i);
                xb(j,2) = x(i+1);
            end
            y1=y2;
        end
        if isempty(xb) 
            disp('no se han encontrado cambios de signo')
        else
            disp(['número de intervalos:' int2str(j)]) 
        end
    end
end

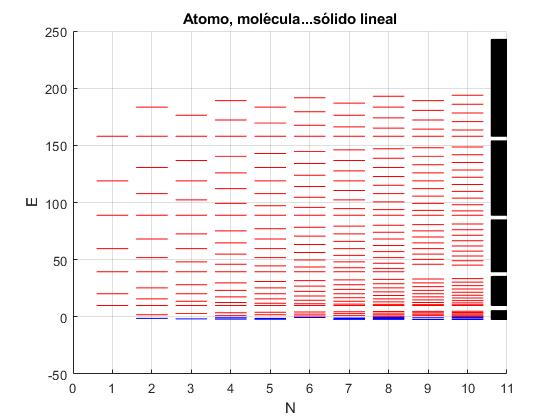
Ampliamos con Zoom in y Pan la gráfica para observar mejor las primeras bandas de energía, o añadimos al código la sentencia, ylim([-4,37])

Referencias

Masatsugu Sei Suzuki. Kronig Penney model. 2018

Marcelo Alonso, Edward J. Finn. Física. Vol. III Fundamentos Cuánticos y Estadísticos. Fondo Educativo Interamericano. 1971, págs. 260-262

L. V. Tarasov. Basic Concepts of Quantum Mechanics. MIR Publishers Moscow. 1980. pp. 223-226