Procedimiento matricial de Numerov

La ecuación de Schrödinger unidimensional independiente del tiempo para el potencial V(x) es

${\displaystyle -\frac{{\hslash }^2}{2m}\frac{d^2\psi (x)}{d{x}^2}+V(x)·\psi (x)=E·\psi (x)}$

Denominaremos

${\displaystyle {\psi }^{(n)}(x)=\frac{d^n\psi (x)}{d{x}^n}}$

Escribimos la ecuación de Schrödinger de la forma

${\displaystyle \begin{array}{l}{\psi }^{(2)}(x)=-\frac{2m}{{\hslash }^2}\left(E-V(x)\right)\psi (x)\\ {\psi }^{(2)}(x)=f(x)\psi (x)\end{array}}$

Desarrollamos en serie la función Ψ(x)

${\displaystyle \begin{array}{l}\psi (x+\delta )=\psi (x)+\delta {\psi }^{(1)}(x)+\frac{1}{2!}{\delta }^2{\psi }^{(2)}(x)+\frac{1}{3!}{\delta }^3{\psi }^{(3)}(x)+\frac{1}{4!}{\delta }^4{\psi }^{(4)}(x)+\mathrm{....}\\ \psi (x-\delta )=\psi (x)-\delta {\psi }^{(1)}(x)+\frac{1}{2!}{\delta }^2{\psi }^{(2)}(x)-\frac{1}{3!}{\delta }^3{\psi }^{(3)}(x)+\frac{1}{4!}{\delta }^4{\psi }^{(4)}(x)+\mathrm{....}\end{array}}$

donde δ es una cantidad pequeña. Sumamos y despejamos Ψ⁽²⁾(x)

${\displaystyle \begin{array}{l}\psi (x-\delta )+\psi (x+\delta )=2\psi (x)+{\delta }^2{\psi }^{(2)}(x)+\frac{1}{12}{\delta }^4{\psi }^{(4)}(x)+\mathrm{....}\\ {\psi }^{(2)}(x)\approx \frac{\psi (x-\delta )+\psi (x+\delta )-2\psi (x)}{{\delta }^2}-\frac{1}{12}{\delta }^2{\psi }^{(4)}(x)\end{array}}$

Calculamos Ψ⁽⁴⁾(x) de forma similar

${\displaystyle {\psi }^{(4)}(x)\approx \frac{{\psi }^{(2)}(x-\delta )+{\psi }^{(2)}(x+\delta )-2{\psi }^{(2)}(x)}{{\delta }^2}=\frac{f(x-\delta )\psi (x-\delta )+f(x+\delta )\psi (x+\delta )-2f(x)\psi (x)}{{\delta }^2}}$

En estas dos últimas ecuaciones, sustituimos Ψ⁽²⁾(x) por f(x)Ψ(x), y Ψ⁽⁴⁾(x) por la expresión anterior

${\displaystyle \begin{array}{l}f(x)\psi (x)\approx \frac{\psi (x-\delta )+\psi (x+\delta )-2\psi (x)}{{\delta }^2}-\frac{1}{12}{\delta }^2\frac{f(x-\delta )\psi (x-\delta )+f(x+\delta )\psi (x+\delta )-2f(x)\psi (x)}{{\delta }^2}\\ \frac{\psi (x-\delta )+\psi (x+\delta )-2\psi (x)}{{\delta }^2}=\frac{1}{12}\left(f(x-\delta )\psi (x-\delta )+f(x+\delta )\psi (x+\delta )+10f(x)\psi (x)\right)\end{array}}$

Denominamos

${\displaystyle \begin{array}{l}{\psi }_{i-1}=\psi (x-\delta ),{\psi }_i=\psi (x),{\psi }_{i+1}=\psi (x+\delta )\\ f_{i-1}=f(x-\delta ),f_i=f(x),f_{i+1}=f(x+\delta )\end{array}}$

La ecuación anterior se escribe

${\displaystyle \frac{{\psi }_{i+1}-2{\psi }_i+{\psi }_{i-1}}{{\delta }^2}=\frac{1}{12}\left(f_{i+1}{\psi }_{i+1}+10f_i{\psi }_i+f_{i-1}{\psi }_{i-1}\right)}$

Donde

${\displaystyle f_{i-1}=-\frac{2m}{{\hslash }^2}\left(E-V_{i-1}\right),f_i=-\frac{2m}{{\hslash }^2}\left(E-V_i\right),f_{i+1}=-\frac{2m}{{\hslash }^2}\left(E-V_{i+1}\right)}$

Se transforma en

${\displaystyle -\frac{{\hslash }^2}{2m}\frac{{\psi }_{i+1}-2{\psi }_i+{\psi }_{i-1}}{{\delta }^2}+\frac{V_{i+1}{\psi }_{i+1}+10V_i{\psi }_i+V_{i-1}{\psi }_{i-1}}{12}=E\frac{{\psi }_{i+1}+10{\psi }_i+{\psi }_{i-1}}{12}}$

Ejemplo, sea N=4. Escribimos las ecuaciones para i=1,2,3,4

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}\frac{{\psi }_2-2{\psi }_1+{\psi }_0}{{\delta }^2}+\frac{V_2{\psi }_2+10V_1{\psi }_1+V_0{\psi }_0}{12}=E\frac{{\psi }_2+10{\psi }_1+{\psi }_0}{12}\\ -\frac{{\hslash }^2}{2m}\frac{{\psi }_3-2{\psi }_2+{\psi }_1}{{\delta }^2}+\frac{V_3{\psi }_3+10V_2{\psi }_2+V_1{\psi }_1}{12}=E\frac{{\psi }_3+10{\psi }_2+{\psi }_1}{12}\\ -\frac{{\hslash }^2}{2m}\frac{{\psi }_4-2{\psi }_3+{\psi }_2}{{\delta }^2}+\frac{V_4{\psi }_4+10V_3{\psi }_3+V_2{\psi }_2}{12}=E\frac{{\psi }_4+10{\psi }_3+{\psi }_2}{12}\\ -\frac{{\hslash }^2}{2m}\frac{{\psi }_5-2{\psi }_4+{\psi }_3}{{\delta }^2}+\frac{V_5{\psi }_5+10V_4{\psi }_4+V_3{\psi }_3}{12}=E\frac{{\psi }_5+10{\psi }_4+{\psi }_3}{12}\\ {\psi }_0=\mathrm{0,}{\psi }_5=0\end{array}}$

En forma matricial

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}\frac{1}{{\delta }^2}\left(\begin{array}{cccc}-2& 1& 0& 0\\ 1& -2& 1& 0\\ 0& 1& -2& 1\\ 0& 0& 1& -2\end{array}\right)\left(\begin{array}{c}{\psi }_1\\ {\psi }_2\\ {\psi }_3\\ {\psi }_4\end{array}\right)+\frac{1}{12}\left(\begin{array}{cccc}10V_1& V_2& 0& 0\\ V_1& 10V_2& V_3& 0\\ 0& V_2& 10V_3& V_4\\ 0& 0& V_3& 10V_4\end{array}\right)\left(\begin{array}{c}{\psi }_1\\ {\psi }_2\\ {\psi }_3\\ {\psi }_4\end{array}\right)=\frac{E}{12}\left(\begin{array}{cccc}10& 1& 0& 0\\ 1& 10& 1& 0\\ 0& 1& 10& 1\\ 0& 0& 1& 10\end{array}\right)\left(\begin{array}{c}{\psi }_1\\ {\psi }_2\\ {\psi }_3\\ {\psi }_4\end{array}\right)\\ -\frac{{\hslash }^2}{2m}\frac{1}{{\delta }^2}\left(\begin{array}{cccc}-2& 1& 0& 0\\ 1& -2& 1& 0\\ 0& 1& -2& 1\\ 0& 0& 1& -2\end{array}\right)\left(\begin{array}{c}{\psi }_1\\ {\psi }_2\\ {\psi }_3\\ {\psi }_4\end{array}\right)+\frac{1}{12}\left(\begin{array}{cccc}10& 1& 0& 0\\ 1& 10& 1& 0\\ 0& 1& 10& 1\\ 0& 0& 1& 10\end{array}\right)\left(\begin{array}{cccc}{V}_1& 0& 0& 0\\ 0& V_2& 0& 0\\ 0& 0& V_3& 0\\ 0& 0& 0& V_4\end{array}\right)\left(\begin{array}{c}{\psi }_1\\ {\psi }_2\\ {\psi }_3\\ {\psi }_4\end{array}\right)=\frac{E}{12}\left(\begin{array}{cccc}10& 1& 0& 0\\ 1& 10& 1& 0\\ 0& 1& 10& 1\\ 0& 0& 1& 10\end{array}\right)\left(\begin{array}{c}{\psi }_1\\ {\psi }_2\\ {\psi }_3\\ {\psi }_4\end{array}\right)\end{array}}$

En general

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}A\psi \text{+}BV\psi \text{=}EB\psi \\ -\frac{{\hslash }^2}{2m}\left(B^{-1}A\right)\psi \text{+}V\psi \text{=}E\psi \\ H\psi =\text{=}E\psi \\ A=\frac{1}{{\delta }^2}\left(\begin{array}{cccccc}-2& 1& 0& 0& 0& \mathrm{...}\\ 1& -2& 1& 0& 0& \mathrm{...}\\ 0& 1& -2& 1& 0& \mathrm{...}\\ 0& 0& 1& -2& 1& \mathrm{...}\\ 0& 0& 0& 1& -2& \mathrm{...}\\ \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}\end{array}\right),B=\frac{1}{12}\left(\begin{array}{cccccc}10& 1& 0& 0& 0& \mathrm{...}\\ 1& 10& 1& 0& 0& \mathrm{...}\\ 0& 1& 10& 1& 0& \mathrm{...}\\ 0& 0& 1& 10& 1& \mathrm{...}\\ 0& 0& 0& 1& 10& \mathrm{...}\\ \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}\end{array}\right)\\ V=\left(\begin{array}{cccccc}{V}_1& 0& 0& 0& 0& \mathrm{...}\\ 0& V_2& 0& 0& 0& \mathrm{...}\\ 0& 1& V_3& 0& 0& \mathrm{...}\\ 0& 0& 0& V_4& 0& \mathrm{...}\\ 0& 0& 0& 0& V_5& \mathrm{...}\\ \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}& \mathrm{...}\end{array}\right),\psi =\left(\begin{array}{c}{\psi }_1\\ {\psi }_2\\ {\psi }_3\\ {\psi }_4\\ {\psi }_5\\ \mathrm{...}\end{array}\right)\\ {\psi }_0=\mathrm{0,}{\psi }_{N+1}=0\end{array}}$

El procedimiento matricial de Numerov consiste en determinar los valores propios (energías) y vectores propios (funciones de onda) de la matriz, H=B^-1A+V

Procedimiento

Hemos calculado los niveles de energía y representado las funciones de onda del potencial en forma de V

x=linspace(0,6,20);
f=@(x) airy(0,-x); %función Ai(x)
r1=raices(f,x);
f=@(x) airy(1,-x); %derivada de Ai(x)
r2=raices(f,x);
En=sort([r1,r2]);
hold on
line([0,-6],[0,6], 'color','r', 'lineWidth',1.5)
line([0,6],[0,6], 'color','r', 'lineWidth',1.5)
n=3;
f=@(x) airy(x-En(n)).^2;
c=1/sqrt(2*integral(f,0,50)); %por simetría
line([-8,8],[En(n),En(n)],'color','k')
g=@(x) c*airy(x-En(n));
x=linspace(0,8,100);
y=g(x);
if rem(n,2)==1 %si es par i=1,3,5
    yy=[fliplr(y)+En(n),y+En(n)];
else %si es impar
    yy=[-fliplr(y)+En(n),y+En(n)];
end 
plot([-fliplr(x),x],yy)
plot(En(n),En(n),'bo','markersize',4,'markerfacecolor','b')
plot(-En(n),En(n),'bo','markersize',4,'markerfacecolor','b')
text(6.5,En(n)+0.2,sprintf('%1.3f',En(n)))
ylim([0,7])
grid on
xlabel('x')
ylabel('\Psi(x)')
title('Potencial V')

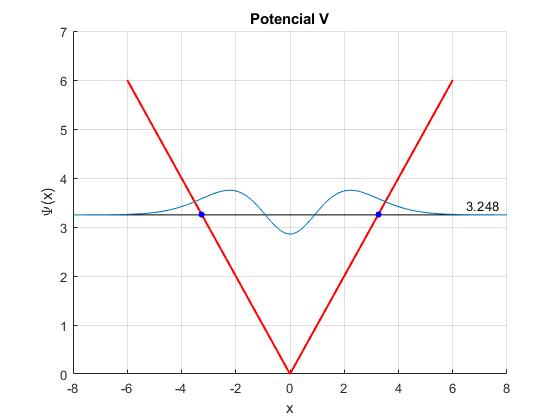
Para un nivel de energía E_n (línea horizontal de color negro) hay dos puntos de intersección con la función potencial V(x) (puntos de color rojo). Cuando nos alejamos hacia la izquierda y hacia la derecha de dichos puntos, la función de onda (en azul) decrece rápidamente a cero

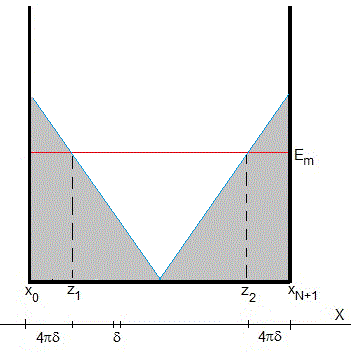
Sea el potencial V(x) de la figura. Se establece una energía máxima E_m. Se calculan las abscisas z₁ y z₂ de los puntos de intersección V(x)=E_m, Cuando el potencial es simétrico z₁=-z₂.

Se establecen un márgen a la izquierda y a la derecha de dichos puntos

Supondremos que la función de onda es nula en x₀ y x_N+1, lo que equivale a resolver la ecuación Schrödinger en el potencial

${\displaystyle \{\begin{array}{l}x\le x_0,\infty \\ x_0<x<x_{N+1},V(x)\\ x\ge x_{N+1},\infty \end{array}}$

Se ha situado el potencial V(x) dentro de un pozo de potencial de altura infinita

El mínimo valor de la longitud de onda de de Broglie es

${\displaystyle \lambda =\frac{h}{mv}=\frac{h}{\sqrt{2m{E}_m}}}$

Estableceremos como espaciado entre puntos, δ=λ

Si el potencial es simétrico, dejamos márgenes iguales de 4πδ, si no es simétrico se pueden dejar márgenes distintos, mayor a la derecha que a la izquierda como se muestra en la figura

Potencial en forma de V

En la página titulada, Potencial en forma de V. Función de Airy hemos obtenido los niveles de energía y representado las funciones de onda para un potencial mg|x|.

Niveles de energía

Exactos

Los niveles de energía E'=αE son las raíces de la función de Airy Ai o de su derivada. La constante α es

${\displaystyle \alpha ={\left(\frac{2}{{\hslash }^{2}m{g}^2}\right)}^{1/3}}$

Establecemos un sistema de unidades en el que las constantes ℏ, m, g valen la unidad, entonces, $\alpha =2^{1/3}$

Los primeros niveles de energía E=E'/α son

x=linspace(0,25,100);
f=@(x) airy(0,-x); %función Ai(x)
r1=raices(f,x);
f=@(x) airy(1,-x); %derivada de Ai(x)
r2=raices(f,x);
alfa=2^(1/3);
En=sort([r1,r2])/alfa;

>> En(1:4)
ans =    0.8086    1.8558    2.5781    3.2446
>> En(10)
ans =    6.3053
>> En(20)
ans =   10.1822
>> En(50)
ans =   18.9469

Aproximados

Establecemos una energía máxima E_m. Las abscisas de los puntos de intersección V(x)=E_m son, ±z₁=±E_m. Establecemos además, un margen a la izquerda y derecha de 4πδ

${\displaystyle \delta =\frac{1}{\sqrt{2E_m}}}$

El número de puntos es el entero más próximo a

${\displaystyle N=\frac{2z_1+8\pi \delta }{\delta }=2\left(\frac{z_1}{\delta }+4\pi \right)}$

Se crean las matrices A, B y E_p con el comando diag, tal como se explica en la página titulada Matrices

Em=20; %energía máxima
h=1/sqrt(2*Em); %paso
z1=Em; %abscida punto de intersección
N=round(2*(z1/h+4*pi)); %número de puntos
xx=-h*N/2+h/2:h:h*N/2-h/2;%abscisas;
%matriz B
B=diag(10*ones(1,N)/12)+diag(ones(1,N-1)/12,1)+diag(ones(1,N-1)/12,-1);
%matriz A
A=diag(-2*ones(1,N)/h^2)+diag(ones(1,N-1)/h^2,1)+diag(ones(1,N-1)/h^2,-1);
%matriz potencial 
f=@(x) abs(x); %función potencial
Ep=diag(f(xx));
%matriz H
H=-inv(B)*A/2+Ep;
[V,D]=eig(H); % valores propios, matriz D. Vectores propios, matriz V
En=sort(diag(D)); %ordena los valores propios de menor a mayor

>> En(1:4)
ans =
    0.8099
    1.8557
    2.5785
    3.2445
>> En(10)
ans =    6.3049
>> En(20)
ans =   10.1806
>> En(50)
ans =   18.9364

Comparación

Los valores exactos y aproximados de los niveles de energía n=1,2,3,4,10,20,50, se recogen en la tabla

Función de onda

Exacta

La función de onda para un nivel de energía E_n es

${\displaystyle {\psi }_n(x)=C·\text{Ai}\left(\alpha (x-E_n)\right)}$

El coeficiente C se calcula de modo que

${\displaystyle {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\left|{\psi }_n(x)\right|}^{2}dx=1}}$

Aproximada

La función de onda correpondiente al valor popio E_n es proporcional al vector propio (columna) n. Utilizamos la función trapz de MATLAB para calcular el coeficiente C de proporcionalidad

Los valores propios de la matriz H aparecen desordendos y hay que ordenarlos de menor a mayor, creamos una función denominada ordenar para que un cambio de orden de un valor propio le suceda el mismo cambio de orden en el vector propio correspondiente

Representamos la función de onda correspondiente al nivel de energía n=50, mediante una curva continua y el vector propio correspondiente al valor popio E_n mediante puntos de color rojo

function numerov_2
%exacto
    x=linspace(0,25,100);
    f=@(x) airy(0,-x); %función Ai(x)
    r1=raices(f,x);
    f=@(x) airy(1,-x); %derivada de Ai(x)
    r2=raices(f,x);
    alfa=2^(1/3);
    E=sort([r1,r2])/alfa;
    
    n=50; %nivel de energía (cambiar)
    f=@(x) airy(alfa*(x-E(n))).^2;
    c=1/sqrt(2*integral(f,0,50)); %por simetría
    g=@(x) airy(alfa*(x-E(n)))*c;
    x=linspace(0,25,400);
    y=g(x);
    if rem(n,2)==1 %si es par i=1,3,5
        yy=[fliplr(y),y];
    else %si es impar
        yy=[-fliplr(y),y];
    end 
    hold on
    plot([-fliplr(x),x],yy)
%aproximado
    Em=20; %energía máxima
    h=1/sqrt(2*Em); %paso
    z1=Em; %abscida punto de intersección, Em=V(x)
    N=round(2*(z1/h+4*pi)); %número de puntos
    xx=-h*N/2+h/2:h:h*N/2-h/2;%abscisas;
    %matriz B
    B=diag(10*ones(1,N)/12)+diag(ones(1,N-1)/12,1)+diag(ones(1,N-1)/12,-1);
    %matriz A
    A=diag(-2*ones(1,N)/h^2)+diag(ones(1,N-1)/h^2,1)+diag(ones(1,N-1)/h^2,-1);
    %matriz potencial V
    f=@(x) abs(x); %función potencial
    Ep=diag(f(xx));
    %matriz H
    H=-inv(B)*A/2 + Ep;
    [V,D]=eig(H); % valores propios, matriz D. Vectores propios, matriz V
    [En,F]=ordenar(diag(D),V);    
    c=1/sqrt(trapz(xx, F(:,n).^2));
    plot(xx,-F(:,n)*c,'ro','markersize',2,'markerfacecolor','r')
    text(-24, 0.1,num2str(En(n)),'VerticalAlignment','bottom', 
'HorizontalAlignment','left');
    hold off
    grid on
    xlabel('x')
    ylabel('\Psi(x)')
    title('Función de onda')
    
    function [x,M]=ordenar(x,M)
        m=length(x);
        for i=1:m
            for j=i+1:m
                if x(i)>x(j)
                    aux=x(j);
                    x(j)=x(i);
                    x(i)=aux;
                    w=M(:,j);
                    M(:,j)=M(:,i);
                    M(:,i)=w;
                 end
            end
        end
    end
end

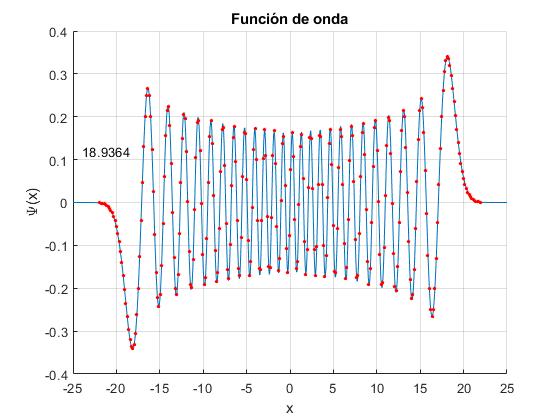
La representación gráfica (en azul) de la función de onda correspondiente al nivel (valor propio) n=50, cuya energía se muestra a la izquierda, junto al vector propio (puntos de color rojo) correspondiente, es un ejemplo de la exactitud del procedimiento numérico de Numerov.

Para ciertos valores de n es necesario cambiar el signo del vector propio -F(:,n)*c para que la función de onda exacta se ajuste con la aproximada. Este vector se encuentra en la línea de código, plot(xx,-F(:,n)*c,'ro','markersize',2,'markerfacecolor','r')

El oscilador armónico cuántico

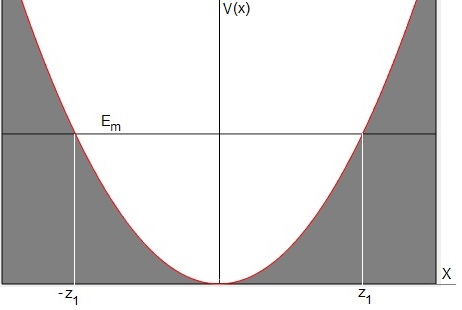
En la página titulada, El oscilador armónico cuántico hemos obtenido los niveles de energía y representado las funciones de onda para un potencial

${\displaystyle V(x)=\frac{1}{2}k{x}^2}$

Tomando una escala de energías y distancias de la forma

${\displaystyle x=\xi \sqrt{\frac{\hslash }{m\omega }}E=\hslash \omega \epsilon \omega =\sqrt{\frac{k}{m}}}$

La ecuación de Schrödinger se transforma en otra más simple

${\displaystyle -\frac{1}{2}\frac{d^2\psi (\xi )}{d{\xi }^2}+\left(\frac{1}{2}{\xi }^2\right)\psi (\xi )=\epsilon \psi (\xi )}$

Exactos

Los niveles de energía son

${\displaystyle {\epsilon }_n=n+\frac{1}{2},n=\mathrm{0,1,2,3...}}$

La función de onda correspondiente al nivel de energía n es

${\displaystyle {\psi }_n(\xi )=\frac{H_n(\xi )}{\sqrt{2^n\sqrt{\pi }n!}}\exp \left(-\frac{{\xi }^2}{2}\right)}$

Aproximados

Establecemos una energía máxima E_m. Las abscisas de los puntos de intersección V(x)=E_m son $z_{\mathrm{1,2}}=\pm \sqrt{2{\epsilon }_m}$. Establecemos además, un margen a la izquerda y derecha de 4πδ

${\displaystyle \delta =\frac{1}{\sqrt{2{\epsilon }_m}}}$

El número de puntos es el entero más próximo a

${\displaystyle N=\frac{2z_1+8\pi \delta }{\delta }=2\left(\frac{z_1}{\delta }+4\pi \right)}$

Se crean las matrices A, B y E_p con el comando diag, tal como se explica en la página titulada Matrices

Los vectores y matrices en MATLAB comienzan con el índice i=1. El nivel de energía n, se corresponde con el índice n+1 en el cálculo aproximado mediante el procedimiento de Numerov

Representamos la función de onda correspondiente al nivel de energía n=10, mediante una curva continua y el vector propio correspondiente al valor popio ε_n mediante puntos de color rojo

function numerov_1
    Em=20; %energía máxima
    h=1/sqrt(2*Em); %paso
    z1=sqrt(2*Em); %abscida punto de intersección, Em=V(x)
    N=round(2*(z1/h+4*pi)); %número de puntos
    x=-h*N/2+h/2:h:h*N/2-h/2;%abscisas;
%exacto
    n=10; %nivel de energía (cambiar)
    y=hermiteH(n,x).*exp(-x.^2/2)/sqrt(2^n*sqrt(pi)*factorial(n));
    hold on
    plot(x,y) 
%aproximado
    %matriz B
    B=diag(10*ones(1,N)/12)+diag(ones(1,N-1)/12,1)+diag(ones(1,N-1)/12,-1);
    %matriz A
    A=diag(-2*ones(1,N)/h^2)+diag(ones(1,N-1)/h^2,1)+diag(ones(1,N-1)/h^2,-1);
    %matriz potencial V
    f=@(x) x.^2/2; %función potencial
    Ep=diag(f(x));
    %matriz H
    H=-inv(B)*A/2+Ep;
    [V,D]=eig(H); % valores propios, matriz D. Vectores propios, matriz V
    [En,F]=ordenar(diag(D),V);    
    c=1/sqrt(trapz(x, F(:,n+1).^2));
    plot(x,-F(:,n+1)*c,'ro','markersize',2,'markerfacecolor','r')
    text(-9, 0.1,num2str(En(n+1)),'VerticalAlignment','bottom', 
'HorizontalAlignment','left');
    hold off
    grid on
    xlabel('x')
    ylabel('\Psi(x)')
    title('Función de onda')
    
    function [x,M]=ordenar(x,M)
        m=length(x);
        for i=1:m
            for j=i+1:m
                if x(i)>x(j)
                    aux=x(j);
                    x(j)=x(i);
                    x(i)=aux;
                    w=M(:,j);
                    M(:,j)=M(:,i);
                    M(:,i)=w;
                 end
            end
        end
    end
end

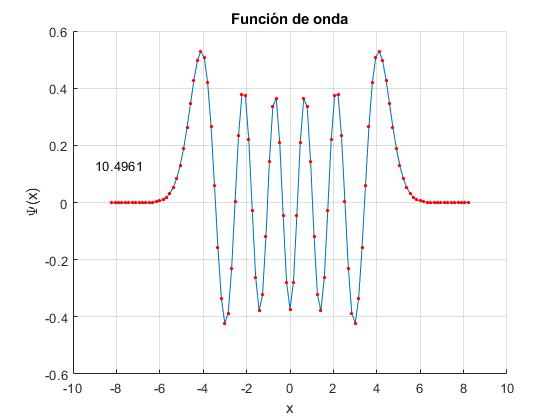
Para n=10, el valor exacto de la energía es ε_n=10+1/2=10.5. El valor aproximado que obtenemos, mediante el procedimiento matricial de Numerov, es 10.4961

Para ciertos valores de n es necesario cambiar el signo del vector propio -F(:,n)*c para que la función de onda exacta se ajuste con la aproximada. Este vector se encuentra en la línea de código, plot(xx,-F(:,n)*c,'ro','markersize',2,'markerfacecolor','r')

Otros potenciales

En este apartado, calculamos los niveles de energía y representamos las funciones de onda para el potencial

${\displaystyle V(x)=a{x}^{2\alpha }+b{x}^2,a>\mathrm{0,}b<0}$

Establecemos un sistema de unidades en el que ℏ=m=1

Representamos el potencial para a=1, b=-4.9497, para tres valores de α=2, 3, 4

a=1;
b=-4.9497;
hold on
for alfa=2:4
    fplot(@(x) a*x.^(2*alfa)+b*x.^2,[-3,3],'displayName',num2str(alfa))
end
hold off
ylim([-10,15])
grid on
legend('-DynamicLegend','location','best')
xlabel('x')
ylabel('V(x)')
title('Potencial')

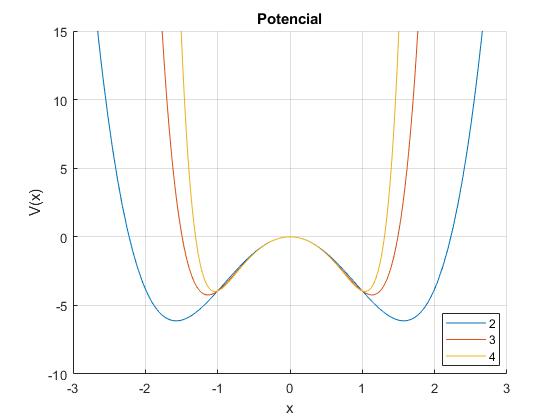
Aplicamos el procedimiento matricial de Numerov para el caso α=3

function numerov_7
    alfa=3;  
    a=1;
    b=-4.9497;
    Em=20; %energía máxima
    raices=roots([1,0,0,0,b,0,-Em]);  %intersección Em=V(x)
    z1=-raices(1);
    h=1/sqrt(2*Em); %paso
    N=round(2*(z1/h+4*pi)); %número de puntos
    x=-h*N/2+h/2:h:h*N/2-h/2;%abscisas;
    %matriz B
    B=diag(10*ones(1,N)/12)+diag(ones(1,N-1)/12,1)+diag(ones(1,N-1)/12,-1);
    %matriz A
    A=diag(-2*ones(1,N)/h^2)+diag(ones(1,N-1)/h^2,1)+diag(ones(1,N-1)/h^2,-1);
    %matriz potencial V
    f=@(x) a*x.^(2*alfa)+b*x.^2; %función potencial
    Ep=diag(f(x));
    %matriz H
    H=-inv(B)*A/2+Ep;
    [V,D]=eig(H); % valores propios, matriz D. Vectores propios, matriz V
    [En,F]=ordenar(diag(D),V);
    fplot(@(x) a*x.^(2*alfa)+b*x.^2,[-3,3]) %energía potencial
    for k=1:7 %niveles de energía
        raices=roots([1,0,0,0,b,0,-En(k)]);
         for m=1:length(raices)
            if isreal(raices(m))
                z1=real(raices(m));
                break;
            end
        end
        line([-z1,z1],[En(k),En(k)],'color','r')
    end
    grid on
    ylim([-5,15])
    xlabel('x')
    ylabel('E_n')
    title('Niveles de energía')
    disp(En(1:10))
    
    %funciones de onda
    figure 
    hold on
    for n=1:3
        c=1/sqrt(trapz(x, F(:,n).^2));
        plot(x,F(:,n)*c,'-o','markersize',2,'markerfacecolor','r',
'displayName',num2str(n))
    end
    hold off
    xlim([-2.5,2.5])
    grid on
    legend('-DynamicLegend','location','best')
    xlabel('x')
    ylabel('\Psi(x)')
    title('Función de onda')
    
    function [x,M]=ordenar(x,M)
        m=length(x);
        for i=1:m
            for j=i+1:m
                if x(i)>x(j)
                    aux=x(j);
                    x(j)=x(i);
                    x(i)=aux;
                    w=M(:,j);
                    M(:,j)=M(:,i);
                    M(:,i)=w;
                 end
            end
        end
    end
end

Se comparan los niveles de energía calculados mediante este script (1), con los que aparecen en la Tabla I (2) del segundo artículo mencionado en las referencias

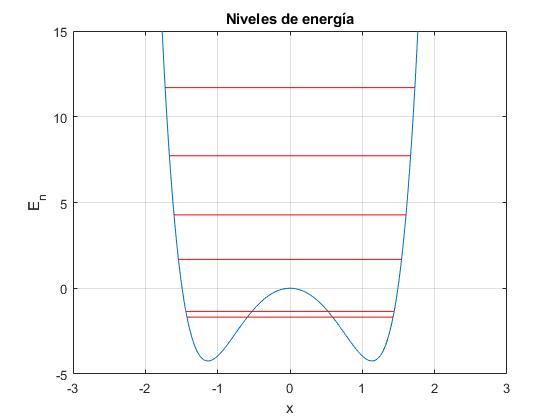
Las funciones de onda correspondientes a los tres primeros niveles de energía son

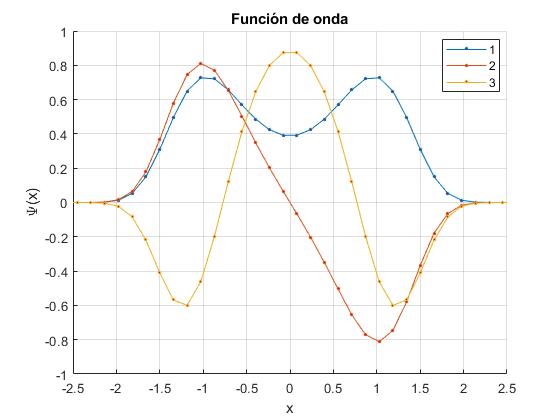
Cambiamos el valor del coeficiente b=-10.6066 manteniendo el valor de α=3

function numerov_8
    alfa=3;  
    a=1;
    b=-10.6066;
    Em=20;   
    raices=roots([1,0,0,0,b,0,-Em]);  %intersección Em=V(x)
    z1=-raices(1);
     h=1/sqrt(2*Em); %paso
     N=round(2*(z1/h+4*pi)); %número de puntos
     x=-h*N/2+h/2:h:h*N/2-h/2;%abscisas;
%aproximado
    %matriz B
    B=diag(10*ones(1,N)/12)+diag(ones(1,N-1)/12,1)+diag(ones(1,N-1)/12,-1);
    %matriz A
    A=diag(-2*ones(1,N)/h^2)+diag(ones(1,N-1)/h^2,1)+diag(ones(1,N-1)/h^2,-1);
    %matriz potencial V
    f=@(x) a*x.^(2*alfa)+b*x.^2; %energía potencial
    Ep=diag(f(x));
    %matriz H
    H=-inv(B)*A/2+Ep;
    [V,D]=eig(H); % valores propios, matriz D. Vectores propios, matriz V
    [En,F]=ordenar(diag(D),V);
    fplot(@(x) a*x.^(2*alfa)+b*x.^2,[-3,3])
    for k=1:8
        raices=roots([1,0,0,0,b,0,-En(k)]);
        for m=1:length(raices)
            if isreal(raices(m))
                z1=real(raices(m));
                break;
            end
        end
        line([-z1,z1],[En(k),En(k)],'color','r')
    end
    grid on
    ylim([-15,15])
    xlabel('x')
    ylabel('E_n')
    title('Niveles de energía')
    disp(En(1:10))
    
    %funciones de onda
    figure 
     hold on
    for n=1:3
        c=1/sqrt(trapz(x, F(:,n).^2));
        plot(x,F(:,n)*c,'-o','markersize',2,'markerfacecolor','r'
,'displayName',num2str(n))
    end
    hold off
    xlim([-2.5,2.5])
    grid on
    legend('-DynamicLegend','location','best')
   xlabel('x')
    ylabel('\Psi(x)')
    title('Función de onda')
    
    function [x,M]=ordenar(x,M)
        m=length(x);
        for i=1:m
            for j=i+1:m
                if x(i)>x(j)
                    aux=x(j);
                    x(j)=x(i);
                    x(i)=aux;
                    w=M(:,j);
                    M(:,j)=M(:,i);
                    M(:,i)=w;
                 end
            end
        end
    end
end

Se comparan los niveles de energía calculados mediante este script (1), con los que aparecen en la Tabla II (2) del segundo artículo mencionado en las referencias

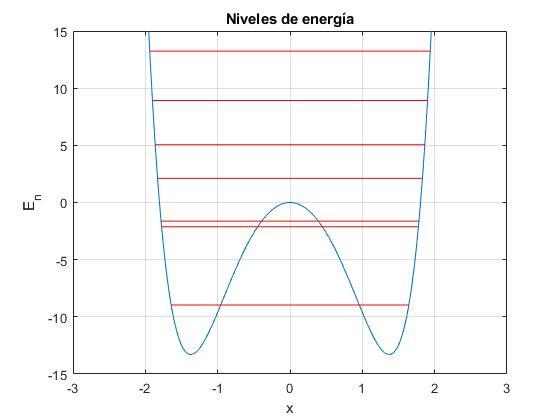
Las funciones de onda correspondientes a los tres primeros niveles de energía son

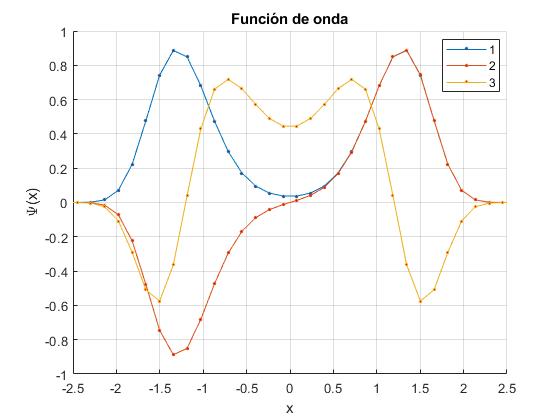
El lector puede cambiar el parámetro α a los valores 1 y 4 y observar los resultados, comparándolos con los de la tabla I (b=-4.9497) y la tabla II (b=-10.6066) del segundo artículo mencionado en las referencias

El potencial Morse

En la página titulada Potencial de Morse y potencial de Pöschl–Teller, hemos calculado los niveles de energía y las funciones de onda de una molécula de CO. Los datos son

• Masa del Carbono, 12.0115, amu
• Masa del Oxígeno, 15.994, amu
• Parámetro D=10.970, eV
• Parámetro α=2.325, Å^-1

La masa reducida m=m₁·m₂/(m₁+m₂)=6.8608 amu

Los puntos de intersección de la recta y=E y la función potencial y=Dexp(-2αx)-2Dexp(-αx) se han calculado en la página titulada el El potencial de Morse

${\displaystyle x_{\mathrm{1,2}}=-\frac{1}{\alpha }\ln \left(1\pm \sqrt{\frac{E+D}{D}}\right)}$

D=10.970; %eV
alfa=2.325; %A^-1
mC=12.0115; %amu
f=@(x) D*exp(-2*alfa*x)-2*D*exp(-alfa*x); %en eV
fplot(f,[-0.35,3])
E=-4;
hold on
line([-0.35,3],[E,E])
x1=-log(1+sqrt((E+D)/D))/alfa;
x2=-log(1-sqrt((E+D)/D))/alfa;
plot(x1,f(x1),'ro','markersize',3,'markerfacecolor','r')
plot(x2,f(x2),'ro','markersize',3,'markerfacecolor','r')
hold off
grid on
xlabel('x')
ylabel('V(x)')
title('Potencial V(x)')

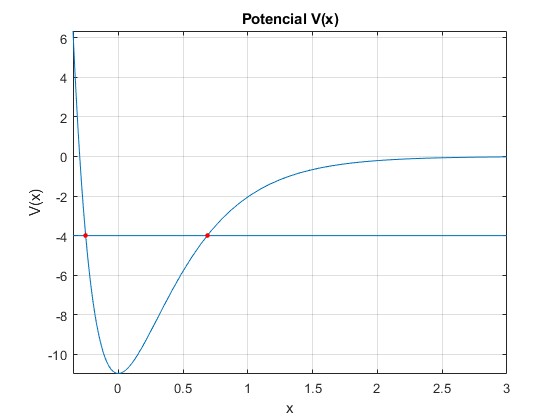
Aplicamos el procedimiento Numerov, comparando la solución analítica y numérica

Expresamos el potencial V(x) en eV y la energía E en eV

  function numerov
    D=10.970; %eV
    alfa=2.325; %A^-1
    mC=12.0115; %amu
    mO=15.9994;
    mu=mO*mC*1.6604e-27/(mO+mC); %masa reducida, en kg
    f=@(x) D*exp(-2*alfa*x)-2*D*exp(-alfa*x); %potencial en eV
    lambda=sqrt(2*mu*D*1.6e-19)/(alfa*1e10*1.0545e-34);
    
    n=2; %numero de nivel (cambiar)
    
    %solución analítica
    E=(-D*1.6e-19+alfa*1e10*1.0545e-34*sqrt(2*D*1.6e-19/mu)*(n+1/2)-
(alfa*1e10*1.0545e-34)^2*(n+1/2).^2/(2*mu))/1.6e-19; %en eV
    z1=-log(1+sqrt((E+D)/D))/alfa;
    z2=-log(1-sqrt((E+D)/D))/alfa;    
    hold on
    text(2*z2, 0,num2str(E),'VerticalAlignment','bottom', 'HorizontalAlignment',
'right');
    g=@(x) fOnda(n,x).^2;
    c2=integral(g,3*z1,5*z2);
    x=linspace(2*z1,2*z2,200);
    y=fOnda(n,x)/sqrt(c2); %normaliza
    plot(x,y)
    
    %procedimiento numérico matricial de Numerov
    Em=-6; %energía máxima
    z1=-log(1+sqrt((Em+D)/D))/alfa;
    z2=-log(1-sqrt((Em+D)/D))/alfa;
    %paso en A, h=6.6256e-34 Js, 1eV=1.6021e-19 J
    h=6.6256e-34*1e10/sqrt(2*mu*D*1.6e-19)/10; 
     xx=z1-4*pi*h:h:z2+4*pi*h;%abscisas;
     N=length(xx);
     constante=1.0545e-34^2/(2*mu*1e-10^2*1.6e-19); %en eV/A^2
     %matriz B
     B=diag(10*ones(1,N)/12)+diag(ones(1,N-1)/12,1)+diag(ones(1,N-1)/12,-1);
     %matriz A
     A=diag(-2*ones(1,N)/h^2)+diag(ones(1,N-1)/h^2,1)+diag(ones(1,N-1)/h^2,-1);
     %matriz potencial V
     Ep=diag(f(xx));
     %matriz H
     H=-constante*inv(B)*A+Ep;
     [V,D]=eig(H); % valores propios, matriz D. Vectores propios, matriz V
    [En,F]=ordenar(diag(D),V);   
    disp(En(1:6))
    c2=1/sqrt(trapz(xx, F(:,n+1).^2));
    plot(xx,-F(:,n+1)*c2,'ro','markersize',2,'markerfacecolor','r')
    text(z1, 0.1,num2str(En(n+1)),'VerticalAlignment','bottom', 
'HorizontalAlignment','left');
    hold off
    grid on
    xlabel('x')
    ylabel('\Psi(x)')
    title('Función de onda')

     
   function res=fOnda(n,x)
        m=round(2*lambda-2*n-1);
        z=2*lambda*exp(-alfa*x);
        res=exp(-z/2).*z.^(lambda-n-1/2).*laguerreL(n,m,z);
    end
         
     function [x,M]=ordenar(x,M)
        m=length(x);
        for i=1:m
            for j=i+1:m
                if x(i)>x(j)
                    aux=x(j);
                    x(j)=x(i);
                    x(i)=aux;
                    w=M(:,j);
                    M(:,j)=M(:,i);
                    M(:,i)=w;
                 end
            end
        end
    end    
 end

Los niveles de energía exactos y aproximados casi coinciden

Se cambia el número de nivel n=0,1,2,3,... en la línea de código n=2; %numero de nivel (cambiar)

• Para n=2



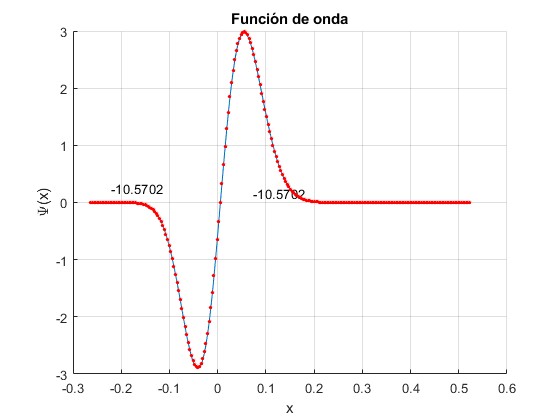
A la izquerda, el valor exacto de la energía del nivel seleccionado, E_n; a la derecha, el valor aproximado

• Para n=5

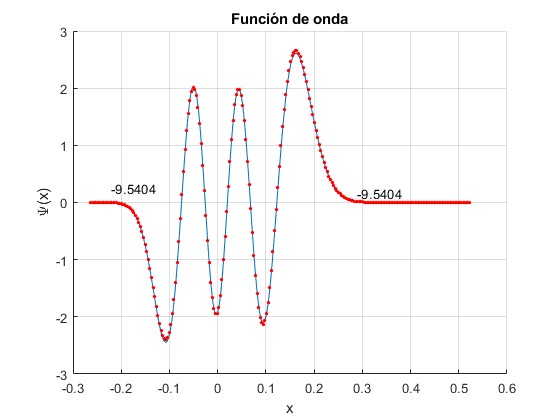
Como podemos apreciar, el procedimiento numérico matricial de Numerov reproduce los cálculos analíticos.

Referencias

Mohandas Pillai, Joshua Goglio, Thad G. Walker. Matrix Numerov method for solving Schrödinger’s equation. Am. J. Phys. 80 (11), November 2012. pp. 1017-1019

N. Al Sdran, F. Maiz. Airy function approach and Numerov method to study the anharmonic oscillator potential V(x)=Ax^2α+Bx². AIP Advances 6, 065323 (2016); https://doi.org/10.1063/1.4954923