En la página titulada Sistema de potenciales delta de Dirac calculamos los niveles de energía y representamos las funciones de onda, para potenciales delta de Dirac negativos. El problema se divide en dos partes: E<0 y E>0. En esta página, los potenciales delta son positivos, por lo que solamente tenemos que estudiar el caso E>0

Sustitución

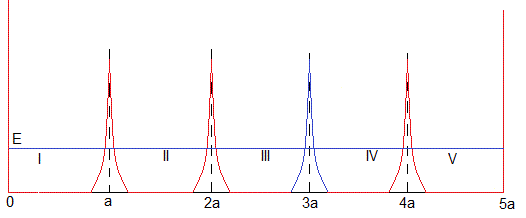
Resolveremos la ecuación de Schrödinger, en un sistema formado por cuatro potenciales delta, igualmente espaciados a, el parámetro del tercero es β y de los restantes α. A partir de este ejemplo, el lector puede generalizar para cualquier número de potenciales iguales e igualmente espaciados con un único defecto, tal como se puede apreciar en el código MATLAB

${\displaystyle -\frac{{\hslash }^2}{2m}\frac{d^2\psi (x)}{d{x}^2}+V(x)·\psi (x)=E·\psi (x)}$

El potencial V(x) es

${\displaystyle \{\begin{array}{l}V(0)=\infty \\ 0<x<a-\epsilon ,V(x)=0\\ a-\epsilon <x<a+\epsilon ,V(x)=\alpha \frac{{\hslash }^2}{2m}\delta (x-a)\\ a+\epsilon <x<2a-\epsilon ,V(x)=0\\ 2a-\epsilon <x<2a+\epsilon ,V(x)=\alpha \frac{{\hslash }^2}{2m}\delta (x-2a)\\ 2a+\epsilon <x<3a-\epsilon ,V(x)=0\\ 3a-\epsilon <x<3a+\epsilon ,V(x)=\beta \frac{{\hslash }^2}{2m}\delta (x-3a)\\ 3a+\epsilon <x<4a-\epsilon ,V(x)=0\\ 4a-\epsilon <x<4a+\epsilon ,V(x)=\alpha \frac{{\hslash }^2}{2m}\delta (x-4a)\\ 4a+\epsilon <x<5a,V(x)=0\\ V(5a)=\infty \end{array}}$

Siendo ε→0, una cantidad que tiende a cero

Las soluciones de la ecuación de Schrödinger en las regiones I, I, III, IV y V con potencial V(x)=0 son

${\displaystyle \begin{array}{l}\frac{d^2\psi }{d{x}^2}+\frac{2m}{{\hslash }^2}E·\psi =\mathrm{0,}E>0\\ \frac{d^2\psi }{d{x}^2}+k^2·\psi =\mathrm{0,}{k}^2=\frac{2m}{{\hslash }^2}E\\ {\psi }_I(x)=A_1\sin (kx)+B_1\cos (kx)\\ {\psi }_{II}(x)=A_2\sin \left(k(x-a)\right)+B_2\cos \left(k(x-a)\right)\\ {\psi }_{III}(x)=A_3\sin \left(k(x-2a)\right)+B_3\cos \left(k(x-a)\right)\\ {\psi }_{IV}(x)=A_4\sin \left(k(x-3a)\right)+B_4\sin \left(k(x-3a)\right)\\ {\psi }_V(x)=A_5\sin \left(k(x-4a)\right)+B_5\sin \left(k(x-4a)\right)\end{array}}$

• Condiciones en los extremos x=0, y x=5a donde V(x)=∞

${\displaystyle \begin{array}{l}{\psi }_I(0)=B_1=0\\ {\psi }_V(5a)=A_5\sin (ka)+B_5\cos (ka)=0\end{array}}$

• En en x=a, x=2a, x=3a y x=4a, la función de onda es continua

${\displaystyle \begin{array}{l}{\psi }_I(a)={\psi }_{II}(a)\\ {\psi }_{II}(2a)={\psi }_{III}(2a)\\ {\psi }_{III}(3a)={\psi }_{IV}(3a)\\ {\psi }_{IV}(4a)={\psi }_V(4a)\\ \{\begin{array}{l}{A}_1\sin (ka)+B_1\cos (ka)=B_2\\ A_2\sin (ka)+B_2\cos (ka)=B_3\\ A_3\sin (ka)+B_3\cos (ka)=B_4\\ A_4\sin (ka)+B_4\cos (ka)=B_5\end{array}\end{array}}$

• La derivada primera de la función de onda NO es continua en x=a, x=2a, x=3a y x=4a

Integramos la ecuación de Schrödinger en el pequeño intervalo de a-ε a a+ε

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}{\displaystyle \underset{a-\epsilon }{\overset{a+\epsilon }{\int }}\frac{d^2\psi (x)}{d{x}^2}}dx+{\displaystyle \underset{a-\epsilon }{\overset{a+\epsilon }{\int }}\alpha \frac{{\hslash }^2}{2m}\delta (x-a)·\psi (x)·dx}=E·{\displaystyle \underset{a-\epsilon }{\overset{a+\epsilon }{\int }}\psi (x)·dx}\\ -\frac{{\hslash }^2}{2m}\underset{\epsilon \to 0}{\lim }\left({\frac{d{\psi }_{II}(x)}{dx}|}_{a+\epsilon }-{\frac{d{\psi }_I(x)}{dx}|}_{a-\epsilon }\right)+\alpha \frac{{\hslash }^2}{2m}{\psi }_{II}(a)=0\\ \underset{\epsilon \to 0}{\lim }\left({k{A}_2\cos \left(k(x-a)\right)-k{B}_2\sin \left(k(x-a)\right)|}_{a+\epsilon }{-\left(k{A}_1\cos (kx)-B_1\sin (kx)\right)|}_{a-\epsilon }\right)-\alpha B_2=0\\ \underset{\epsilon \to 0}{\lim }\left(\left(k{A}_2\cos \left(k\epsilon \right)-k{B}_2\sin \left(k\epsilon \right)\right)-\left(k{A}_1\cos \left(k(a-\epsilon )\right)-k{B}_1\sin \left(k(a-\epsilon )\right)\right)\right)-\alpha B_2=0\\ k{A}_2-\left(k{A}_1\cos \left(ka\right)-k{B}_1\sin \left(ka)\right)\right)-\alpha B_2=0\end{array}}$

De modo similar, establecemos las otras tres ecuaciones que relacionan los coeficientes en x=2a (parámetro α), en x=3a (parámetro β) y x=4a (parámetro α)

${\displaystyle \{\begin{array}{l}{A}_1\cos \left(ka\right)-B_1\sin (ka)=A_2-\frac{\alpha }{k}{B}_2\\ A_2\cos \left(ka\right)-B_2\sin (ka)=A_3-\frac{\alpha }{k}{B}_3\\ A_3\cos \left(ka\right)-B_3\sin (ka)=A_4-\frac{\beta }{k}{B}_4\\ A_4\cos \left(ka\right)-B_4\sin (ka)=A_5-\frac{\alpha }{k}{B}_5\end{array}}$

En forma matricial, la relación entre los coeficientes es

${\displaystyle \begin{array}{l}\left(\begin{array}{cc}\sin (ka)& \cos (ka)\\ \cos (ka)& -\sin (ka)\end{array}\right)\left(\begin{array}{c}{A}_1\\ B_1\end{array}\right)=\left(\begin{array}{cc}0& 1\\ 1& -\frac{\alpha }{k}\end{array}\right)\left(\begin{array}{c}{A}_2\\ B_2\end{array}\right)\\ \left(\begin{array}{cc}\sin (ka)& \cos (ka)\\ \cos (ka)& -\sin (ka)\end{array}\right)\left(\begin{array}{c}{A}_2\\ B_2\end{array}\right)=\left(\begin{array}{cc}0& 1\\ 1& -\frac{\alpha }{k}\end{array}\right)\left(\begin{array}{c}{A}_3\\ B_3\end{array}\right)\\ \left(\begin{array}{cc}\sin (ka)& \cos (ka)\\ \cos (ka)& -\sin (ka)\end{array}\right)\left(\begin{array}{c}{A}_3\\ B_3\end{array}\right)=\left(\begin{array}{cc}0& 1\\ 1& -\frac{\beta }{k}\end{array}\right)\left(\begin{array}{c}{A}_4\\ B_4\end{array}\right)\\ \left(\begin{array}{cc}\sin (ka)& \cos (ka)\\ \cos (ka)& -\sin (ka)\end{array}\right)\left(\begin{array}{c}{A}_4\\ B_4\end{array}\right)=\left(\begin{array}{cc}0& 1\\ 1& -\frac{\alpha }{k}\end{array}\right)\left(\begin{array}{c}{A}_5\\ B_5\end{array}\right)\end{array}}$

Niveles de energía

Relacionamos A₁ y B₁ con A₅ y B₅

${\displaystyle \begin{array}{l}\left(\begin{array}{c}{A}_1\\ B_1\end{array}\right)={\left(M^{-1}{N}_{\alpha }\right)}^2\left(M^{-1}{N}_{\beta }\right)\left(M^{-1}{N}_{\alpha }\right)\left(\begin{array}{c}{A}_5\\ B_5\end{array}\right)\\ M^{-1}={\left(\begin{array}{cc}\sin (ka)& \cos (ka)\\ \cos (ka)& -\sin (ka)\end{array}\right)}^{-1}=\left(\begin{array}{cc}\sin (ka)& \cos (ka)\\ \cos (ka)& -\sin (ka)\end{array}\right)\\ N_{\alpha }=\left(\begin{array}{cc}0& 1\\ 1& -\frac{\alpha }{k}\end{array}\right),N_{\beta }=\left(\begin{array}{cc}0& 1\\ 1& -\frac{\beta }{k}\end{array}\right)\end{array}}$

Teniendo en cuenta, la relaciones en los extremos, en x=0 (B₁=0) y en x=5a, (A₅sin(ka)+B₅cos(ka)=0), obtenemos la ecuación transcendente

${\displaystyle \begin{array}{l}\left(\begin{array}{c}{A}_1\\ 0\end{array}\right)=\left(\begin{array}{cc}{t}_{11}& t_{12}\\ t_{21}& t_{22}\end{array}\right)\left(\begin{array}{c}{A}_5\\ -A_5\frac{\sin (ka)}{\cos (ka)}\end{array}\right)\\ t_{21}\cos (ka)-t_{22}\sin (ka)=0\end{array}}$

Representamos los niveles de energía para un sistama de N=4 potenciales delta de Dirac, fijamos la separación constante a=1, el parámetro α=2, de todos los potenciales excepto el tercero, n=3, cuyo parámetro β va cambiando entre 0 y 10

function delta_dirac_30
    a=1;
    alfa=2;
    N=4;
    n=3; %posición defecto
    hold on
    for beta=0:0.5:10
        ff=@(x) niveles(x);
        xb=buscar_intervalos(ff,0.1,4,50);
        nb=size(xb);
        for m=1:nb(1)
            raiz=fzero(ff,[xb(m,1) xb(m,2)]);
            plot(beta,raiz^2,'ro','markersize',3,'markerfacecolor','r')
        end
    end
    line([alfa,alfa],[0,11],'lineStyle','--')
    ylim([0,11])
    hold off
    grid on
    xlabel('\beta');
    ylabel('E')
    title('Defecto en el sólido lineal')
  
    
    function res=niveles(k)
        T=eye(2);
        Ma=[0,1; 1,-alfa/k];  
        Mb=[0,1; 1,-beta/k];  
        MI=[sin(k*a),cos(k*a);cos(k*a),-sin(k*a)];
       for s=N:-1:n+1
             T=(MI*Ma)*T;
       end
        T=(MI*Mb)*T;
       for s=n-1:-1:1
             T=(MI*Ma)*T;
       end
        res=T(2,1)*cos(k*a)-T(2,2)*sin(k*a);
    end

   function xb = buscar_intervalos(f,a,b,n)
        x = a:(b-a)/n:b;
        j = 0; 
        y1=f(x(1));
        xb=[];
        for i = 1:length(x)-1
            y2=f(x(i+1));
            if sign(y1) ~= sign(y2) 
                j = j + 1;
                xb(j,1) = x(i);
                xb(j,2) = x(i+1);
            end
            y1=y2;
        end
        if isempty(xb) 
            disp('no se han encontrado cambios de signo')
        else
            disp(['número de intervalos:' int2str(j)]) 
        end
    end
end

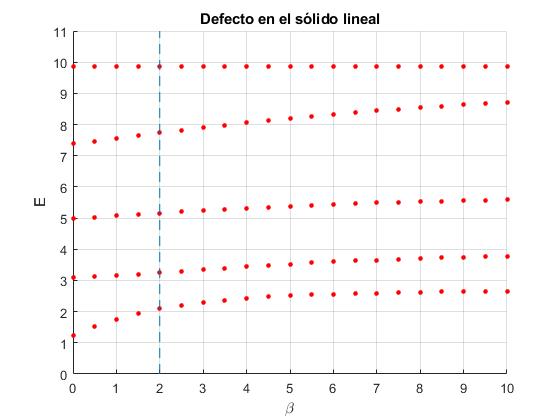
Cuando el parámetro β=α=2, línea a trazos, no hay defecto.

Funciones de onda

Dados los coeficientes A₁ y B₁=0, obtenemos los coeficientes A₂ y B₂, A₃ y B₃, A₄ y B₄, A₅ y B₅. En forma matricial

${\displaystyle \begin{array}{l}\left(\begin{array}{c}{A}_2\\ B_2\end{array}\right)={\left(\begin{array}{cc}0& 1\\ 1& \frac{\alpha }{k}\end{array}\right)}^{-1}\left(\begin{array}{cc}\sin (ka)& \cos (ka)\\ \cos (ka)& -\sin (ka)\end{array}\right)\left(\begin{array}{c}{A}_1\\ B_1\end{array}\right)\\ \left(\begin{array}{c}{A}_3\\ B_3\end{array}\right)={\left(\begin{array}{cc}0& 1\\ 1& \frac{\alpha }{k}\end{array}\right)}^{-1}\left(\begin{array}{cc}\sin (ka)& \cos (ka)\\ \cos (ka)& -\sin (ka)\end{array}\right)\left(\begin{array}{c}{A}_2\\ B_2\end{array}\right)\\ \left(\begin{array}{c}{A}_4\\ B_4\end{array}\right)={\left(\begin{array}{cc}0& 1\\ 1& \frac{\beta }{k}\end{array}\right)}^{-1}\left(\begin{array}{cc}\sin (ka)& \cos (ka)\\ \cos (ka)& -\sin (ka)\end{array}\right)\left(\begin{array}{c}{A}_3\\ B_3\end{array}\right)\\ \left(\begin{array}{c}{A}_5\\ B_5\end{array}\right)={\left(\begin{array}{cc}0& 1\\ 1& \frac{\alpha }{k}\end{array}\right)}^{-1}\left(\begin{array}{cc}\sin (ka)& \cos (ka)\\ \cos (ka)& -\sin (ka)\end{array}\right)\left(\begin{array}{c}{A}_4\\ B_4\end{array}\right)\end{array}}$

El coeficiente A₁ se determina de modo que la suma

${\displaystyle \begin{array}{l}{\displaystyle \sum _{n=1}^{N+1}{\displaystyle \underset{(n-1)a}{\overset{na}{\int }}{\left(A_n\sin \left(k(x-(n-1)a)\right)+B_n\cos \left(k(x-(n-1)a)\right)\right)}^{2}dx}}=1\\ {\displaystyle \sum _{n=1}^{N+1}\left\{\frac{A_n^2}{2}\left(a-\frac{\sin \left(2ka\right)}{2k}\right)+\frac{B_n^2}{2}\left(a+\frac{\sin \left(2ka\right)}{2k}\right)-\frac{A_n{B}_n}{2k}\left(\cos \left(2ka\right)-1\right)\right\}}=1\end{array}}$

Representamos las funciones de onda correspondientes a los dos primeros niveles de energía para un sistama de N=4 potenciales delta de Dirac, fijamos la separación constante a=1, el parámetro α=2, de todos los potenciales excepto el tercero, n=3, cuyo parámetro β=0.5

function delta_dirac_27
    a=1;
    alfa=2;
    beta=0.5;
    N=4;
    n=3; %posición defecto
    ff=@(x) niveles(x);
    xb=buscar_intervalos(ff,0.1,4,50);
    nb=size(xb);
    kn=zeros(1,nb(1));
    for m=1:nb(1)
        kn(m)=fzero(ff,[xb(m,1) xb(m,2)]);
    end
    disp(kn)

    A=zeros(1,N+1);
    B=zeros(1,N+1);
    A(1)=1; B(1)=0;
    for k=kn(1:2)
        NaI=[alfa/k,1;1,0];  
        NbI=[beta/k,1;1,0];  
        M=[sin(k*a),cos(k*a);cos(k*a),-sin(k*a)];
        suma=A(1)^2*(a-sin(2*k*a)/(2*k))/2+B(1)^2*(a+sin(2*k*a)/(2*k))/2-
A(1)*B(1)*(cos(2*k*a)-1)/(2*k);
        for m=1:n-1
            Z=(NaI*M)*[A(m);B(m)];
            A(m+1)=Z(1);
            B(m+1)=Z(2);
            suma=suma+A(m+1)^2*(a-sin(2*k*a)/(2*k))/2+B(m+1)^2*(a+sin(2*k*a)/(2*k))
/2-A(m+1)*B(m+1)*(cos(2*k*a)-1)/(2*k);
        end
        m=n;
        Z=(NbI*M)*[A(m);B(m)];
        A(m+1)=Z(1);
        B(m+1)=Z(2);
        suma=suma+A(m+1)^2*(a-sin(2*k*a)/(2*k))/2+B(m+1)^2*(a+sin(2*k*a)/(2*k))
/2-A(m+1)*B(m+1)*(cos(2*k*a)-1)/(2*k);
        for m=n+1:N
            Z=(NaI*M)*[A(m);B(m)];
            A(m+1)=Z(1);
            B(m+1)=Z(2);
            suma=suma+A(m+1)^2*(a-sin(2*k*a)/(2*k))/2+B(m+1)^2*(a+sin(2*k*a)/(2*k))
/2-A(m+1)*B(m+1)*(cos(2*k*a)-1)/(2*k);
        end
        hold on
        for m=0:N
            fplot(@(x) (A(m+1)*sin(k*(x-m*a))+B(m+1)*cos(k*(x-m*a)))/sqrt(suma),
[m*a,(m+1)*a])
        end
    end
    hold off
    grid on
    xlabel('x')
    ylabel('\Phi(x)')
    title('Funciones de onda')

    function res=niveles(k)
        T=eye(2);
        Ma=[0,1; 1,-alfa/k];  
        Mb=[0,1; 1,-beta/k];  
        MI=[sin(k*a),cos(k*a);cos(k*a),-sin(k*a)];
       for s=N:-1:n+1
             T=(MI*Ma)*T;
       end
        T=(MI*Mb)*T;
       for s=n-1:-1:1
             T=(MI*Ma)*T;
       end
        res=T(2,1)*cos(k*a)-T(2,2)*sin(k*a);
    end

   function xb = buscar_intervalos(f,a,b,n)
        x = a:(b-a)/n:b;
        j = 0; 
        y1=f(x(1));
        xb=[];
        for i = 1:length(x)-1
            y2=f(x(i+1));
            if sign(y1) ~= sign(y2) 
                j = j + 1;
                xb(j,1) = x(i);
                xb(j,2) = x(i+1);
            end
            y1=y2;
        end
        if isempty(xb) 
            disp('no se han encontrado cambios de signo')
        else
            disp(['número de intervalos:' int2str(j)]) 
        end
    end
end

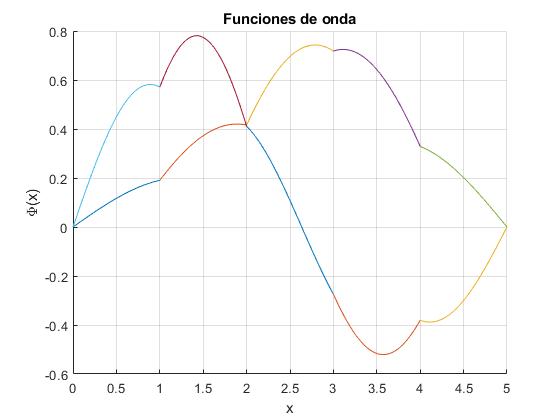
Las primeras raíces k de la ecuación transcendente son

 1.0145    1.8762    3.1416    3.5450

Desplazamiento

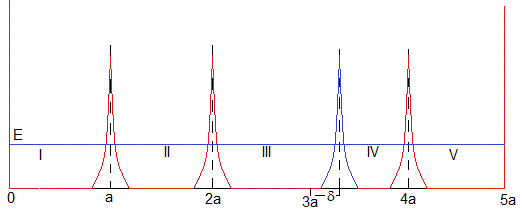
Resolveremos la ecuación de Schrödinger, en un sistema formado por cuatro potenciales delta, igualmente espaciados a, el parámetro de todos los potenciales es α. El tercer potencial delta se desplaza δ<a. A partir de este ejemplo, el lector puede generalizar para cualquier número de potenciales iguales con un único defecto, tal como se puede apreciar en el código MATLAB

El potencial V(x) es

${\displaystyle \{\begin{array}{l}V(0)=\infty \\ 0<x<a-\epsilon ,V(x)=0\\ a-\epsilon <x<a+\epsilon ,V(x)=\alpha \frac{{\hslash }^2}{2m}\delta (x-a)\\ a+\epsilon <x<2a-\epsilon ,V(x)=0\\ 2a-\epsilon <x<2a+\epsilon ,V(x)=\alpha \frac{{\hslash }^2}{2m}\delta (x-2a)\\ 2a+\epsilon <x<3a-\epsilon ,V(x)=0\\ 3a+\delta -\epsilon <x<3a+\delta +\epsilon ,V(x)=\alpha \frac{{\hslash }^2}{2m}\delta (x-3a-\delta )\\ 3a+\delta +\epsilon <x<4a-\epsilon ,V(x)=0\\ 4a-\epsilon <x<4a+\epsilon ,V(x)=\alpha \frac{{\hslash }^2}{2m}\delta (x-4a)\\ 4a+\epsilon <x<5a,V(x)=0\\ V(5a)=\infty \end{array}}$

Siendo ε→0, una cantidad que tiende a cero

Las soluciones de la ecuación de Schrödinger en las regiones I, I, III, IV y V con potencial V(x)=0 son

${\displaystyle \begin{array}{l}\frac{d^2\psi }{d{x}^2}+\frac{2m}{{\hslash }^2}E·\psi =\mathrm{0,}E>0\\ \frac{d^2\psi }{d{x}^2}+k^2·\psi =\mathrm{0,}{k}^2=\frac{2m}{{\hslash }^2}E\\ {\psi }_I(x)=A_1\sin (kx)+B_1\cos (kx)\\ {\psi }_{II}(x)=A_2\sin \left(k(x-a)\right)+B_2\cos \left(k(x-a)\right)\\ {\psi }_{III}(x)=A_3\sin \left(k(x-2a)\right)+B_3\cos \left(k(x-a)\right)\\ {\psi }_{IV}(x)=A_4\sin \left(k(x-3a-\delta )\right)+B_4\cos \left(k(x-3a-\delta )\right)\\ {\psi }_V(x)=A_5\sin \left(k(x-4a)\right)+B_5\cos \left(k(x-4a)\right)\end{array}}$

• Condiciones en los extremos x=0, y x=5a donde V(x)=∞

${\displaystyle \begin{array}{l}{\psi }_I(0)=B_1=0\\ {\psi }_V(5a)=A_5\sin (ka)+B_5\cos (ka)=0\end{array}}$

• En en x=a, x=2a, x=3a+δ y x=4a, la función de onda es continua

${\displaystyle \begin{array}{l}{\psi }_I(a)={\psi }_{II}(a)\\ {\psi }_{II}(2a)={\psi }_{III}(2a)\\ {\psi }_{III}(3a+\delta )={\psi }_{IV}(3a+\delta )\\ {\psi }_{IV}(4a)={\psi }_V(4a)\\ \{\begin{array}{l}{A}_1\sin (ka)+B_1\cos (ka)=B_2\\ A_2\sin (ka)+B_2\cos (ka)=B_3\\ A_3\sin \left(k(a+\delta )\right)+B_3\cos \left(k(a+\delta )\right)=B_4\\ A_4\sin \left(k(a-\delta )\right)+B_4\cos \left(k(a-\delta )\right)=B_5\end{array}\end{array}}$

• La derivada primera de la función de onda NO es continua en x=a, x=2a, x=3a+δ y x=4a. En la sección anterior hemos visto cómo se relacionan los coeficientes. En ésta, examinamos las posiciones x=3a+δ y x=4a

Integramos la ecuación de Schrödinger en el pequeño intervalo de 3a+δ-ε a 3a+δ+ε

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}{\displaystyle \underset{3a+\delta -\epsilon }{\overset{3a+\delta +\epsilon }{\int }}\frac{d^2\psi (x)}{d{x}^2}}dx+{\displaystyle \underset{3a+\delta -\epsilon }{\overset{3a+\delta +\epsilon }{\int }}\alpha \frac{{\hslash }^2}{2m}\delta (x-3a-\delta )·\psi (x)·dx}=E·{\displaystyle \underset{3a+\delta -\epsilon }{\overset{3a+\delta +\epsilon }{\int }}\psi (x)·dx}\\ -\frac{{\hslash }^2}{2m}\underset{\epsilon \to 0}{\lim }\left({\frac{d{\psi }_{IV}(x)}{dx}|}_{3a+\delta +\epsilon }-{\frac{d{\psi }_{III}(x)}{dx}|}_{3a+\delta -\epsilon }\right)+\alpha \frac{{\hslash }^2}{2m}{\psi }_{IV}(3a+\delta )=0\\ \underset{\epsilon \to 0}{\lim }\left({k{A}_4\cos \left(k(x-3a-\delta )\right)-k{B}_4\sin \left(k(x-3a-\delta )\right)|}_{3a+\delta +\epsilon }{-\left(k{A}_3\cos \left(k(x-2a)\right)-B_3\sin \left(k(x-2a)\right)\right)|}_{3a+\delta -\epsilon }\right)-\alpha B_4=0\\ \underset{\epsilon \to 0}{\lim }\left(\left(k{A}_4\cos \left(k\epsilon \right)-k{B}_4\sin \left(k\epsilon \right)\right)-\left(k{A}_3\cos \left(k(a+\delta -\epsilon )\right)-k{B}_3\sin \left(k(a+\delta -\epsilon )\right)\right)\right)-\alpha B_4=0\\ k{A}_4-\left(k{A}_3\cos \left(k(a+\delta )\right)-k{B}_3\sin \left(k(a+\delta )\right)\right)-\alpha B_4=0\end{array}}$

Integramos la ecuación de Schrödinger en el pequeño intervalo de 4a-ε a 4a+ε

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}{\displaystyle \underset{4a-\epsilon }{\overset{4a+\epsilon }{\int }}\frac{d^2\psi (x)}{d{x}^2}}dx+{\displaystyle \underset{4a-\epsilon }{\overset{4a+\epsilon }{\int }}\alpha \frac{{\hslash }^2}{2m}\delta (x-4a)·\psi (x)·dx}=E·{\displaystyle \underset{4a-\epsilon }{\overset{4a+\epsilon }{\int }}\psi (x)·dx}\\ -\frac{{\hslash }^2}{2m}\underset{\epsilon \to 0}{\lim }\left({\frac{d{\psi }_V(x)}{dx}|}_{4a+\epsilon }-{\frac{d{\psi }_{IV}(x)}{dx}|}_{4a-\epsilon }\right)+\alpha \frac{{\hslash }^2}{2m}{\psi }_V(4a)=0\\ \underset{\epsilon \to 0}{\lim }\left({k{A}_5\cos \left(k(x-4a)\right)-k{B}_5\sin \left(k(x-4a)\right)|}_{4a+\epsilon }{-\left(k{A}_4\cos \left(k(x-3a-\delta )\right)-B_4\sin \left(k(x-3a-\delta )\right)\right)|}_{4a-\epsilon }\right)-\alpha B_5=0\\ \underset{\epsilon \to 0}{\lim }\left(\left(k{A}_5\cos \left(k\epsilon \right)-k{B}_5\sin \left(k\epsilon \right)\right)-\left(k{A}_4\cos \left(k(a-\delta -\epsilon )\right)-k{B}_4\sin \left(k(a-\delta -\epsilon )\right)\right)\right)-\alpha B_5=0\\ k{A}_5-\left(k{A}_4\cos \left(k(a-\delta )\right)-k{B}_4\sin \left(k(a-\delta )\right)\right)-\alpha B_5=0\end{array}}$

Las cuatro ecuaciones que relacionan los coeficientes en x=a, x=2a, x=3a+δ y x=4a son

${\displaystyle \{\begin{array}{l}{A}_1\cos \left(ka\right)-B_1\sin (ka)=A_2-\frac{\alpha }{k}{B}_2\\ A_2\cos \left(ka\right)-B_2\sin (ka)=A_3-\frac{\alpha }{k}{B}_3\\ A_3\cos \left(k(a+\delta )\right)-B_3\sin \left(k(a+\delta )\right)=A_4-\frac{\alpha }{k}{B}_4\\ A_4\cos \left(k(a-\delta )\right)-B_4\sin \left(k(a-\delta )\right)=A_5-\frac{\alpha }{k}{B}_5\end{array}}$

En forma matricial, la relación entre los coeficientes es

${\displaystyle \begin{array}{l}\left(\begin{array}{cc}\sin (ka)& \cos (ka)\\ \cos (ka)& -\sin (ka)\end{array}\right)\left(\begin{array}{c}{A}_1\\ B_1\end{array}\right)=\left(\begin{array}{cc}0& 1\\ 1& -\frac{\alpha }{k}\end{array}\right)\left(\begin{array}{c}{A}_2\\ B_2\end{array}\right)\\ \left(\begin{array}{cc}\sin (ka)& \cos (ka)\\ \cos (ka)& -\sin (ka)\end{array}\right)\left(\begin{array}{c}{A}_2\\ B_2\end{array}\right)=\left(\begin{array}{cc}0& 1\\ 1& -\frac{\alpha }{k}\end{array}\right)\left(\begin{array}{c}{A}_3\\ B_3\end{array}\right)\\ \left(\begin{array}{cc}\sin \left(k(a+\delta )\right)& \cos \left(k(a+\delta )\right)\\ \cos \left(k(a+\delta )\right)& -\sin \left(k(a+\delta )\right)\end{array}\right)\left(\begin{array}{c}{A}_3\\ B_3\end{array}\right)=\left(\begin{array}{cc}0& 1\\ 1& -\frac{\alpha }{k}\end{array}\right)\left(\begin{array}{c}{A}_4\\ B_4\end{array}\right)\\ \left(\begin{array}{cc}\sin \left(k(a-\delta )\right)& \cos \left(k(a-\delta )\right)\\ \cos \left(k(a-\delta )\right)& -\sin \left(k(a-\delta )\right)\end{array}\right)\left(\begin{array}{c}{A}_4\\ B_4\end{array}\right)=\left(\begin{array}{cc}0& 1\\ 1& -\frac{\alpha }{k}\end{array}\right)\left(\begin{array}{c}{A}_5\\ B_5\end{array}\right)\end{array}}$

Niveles de energía

Relacionamos A₁ y B₁ con A₅ y B₅

${\displaystyle \begin{array}{l}\left(\begin{array}{c}{A}_1\\ B_1\end{array}\right)={\left(M^{-1}N\right)}^2\left(M_{+\delta }^{-1}N\right)\left(M_{-\delta }^{-1}N\right)\left(\begin{array}{c}{A}_5\\ B_5\end{array}\right)\\ M^{-1}={\left(\begin{array}{cc}\sin (ka)& \cos (ka)\\ \cos (ka)& -\sin (ka)\end{array}\right)}^{-1}=\left(\begin{array}{cc}\sin (ka)& \cos (ka)\\ \cos (ka)& -\sin (ka)\end{array}\right)\\ N=\left(\begin{array}{cc}0& 1\\ 1& -\frac{\alpha }{k}\end{array}\right)\end{array}}$

Representamos los niveles de energía para un sistama de N=4 potenciales delta de Dirac, fijamos la separación constante a=1, el parámetro α=2, de todos los potenciales. El tercero, n=3, se desplaza δ<a que va cambiando entre 0 y 0.9

function delta_dirac_29
    a=1;
    alfa=2;
    N=4;
    n=3; %posición defecto
    hold on
    for delta=linspace(0,0.9,20)
        ff=@(x) niveles(x);
        xb=buscar_intervalos(ff,0.1,4,50);
        nb=size(xb);
        for m=1:nb(1)
            raiz=fzero(ff,[xb(m,1) xb(m,2)]);
            plot(delta,raiz^2,'ro','markersize',3,'markerfacecolor','r')
        end
    end
    hold off
    grid on
    ylim([0,11])
    xlabel('\delta');
    ylabel('E')
    title('Defecto en el sólido lineal')

    function res=niveles(k)
        T=eye(2);
        M=[0,1; 1,-alfa/k];  
        MI=[sin(k*a),cos(k*a);cos(k*a),-sin(k*a)];
        MIa=[sin(k*(a+delta)),cos(k*(a+delta));cos(k*(a+delta)),-sin(k*(a+delta))];
        MIb=[sin(k*(a-delta)),cos(k*(a-delta));cos(k*(a-delta)),-sin(k*(a-delta))];
        for s=N:-1:n+2
             T=(MI*M)*T;
        end
        T=(MIb*M)*T;
        T=(MIa*M)*T;
        for s=n-1:-1:1
             T=(MI*M)*T;
        end
        res=T(2,1)*cos(k*a)-T(2,2)*sin(k*a);
    end

   function xb = buscar_intervalos(f,a,b,n)
        x = a:(b-a)/n:b;
        j = 0; 
        y1=f(x(1));
        xb=[];
        for i = 1:length(x)-1
            y2=f(x(i+1));
            if sign(y1) ~= sign(y2) 
                j = j + 1;
                xb(j,1) = x(i);
                xb(j,2) = x(i+1);
            end
            y1=y2;
        end
        if isempty(xb) 
            disp('no se han encontrado cambios de signo')
        else
            disp(['número de intervalos:' int2str(j)]) 
        end
    end
end

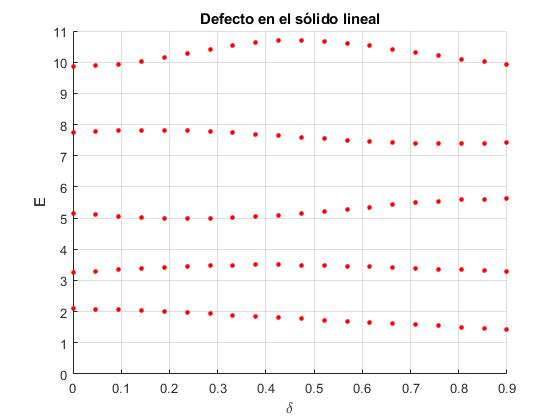
Para δ=0, no hay defecto

Funciones de onda

Dados los coeficientes A₁ y B₁=0, obtenemos los coeficientes A₂ y B₂, A₃ y B₃, A₄ y B₄, A₅ y B₅. En forma matricial

${\displaystyle \begin{array}{l}\left(\begin{array}{c}{A}_2\\ B_2\end{array}\right)={\left(\begin{array}{cc}0& 1\\ 1& -\frac{\alpha }{k}\end{array}\right)}^{-1}\left(\begin{array}{cc}\sin (ka)& \cos (ka)\\ \cos (ka)& -\sin (ka)\end{array}\right)\left(\begin{array}{c}{A}_1\\ B_1\end{array}\right)\\ \left(\begin{array}{c}{A}_3\\ B_3\end{array}\right)={\left(\begin{array}{cc}0& 1\\ 1& -\frac{\alpha }{k}\end{array}\right)}^{-1}\left(\begin{array}{cc}\sin (ka)& \cos (ka)\\ \cos (ka)& -\sin (ka)\end{array}\right)\left(\begin{array}{c}{A}_2\\ B_2\end{array}\right)\\ \left(\begin{array}{c}{A}_4\\ B_4\end{array}\right)={\left(\begin{array}{cc}0& 1\\ 1& -\frac{\alpha }{k}\end{array}\right)}^{-1}\left(\begin{array}{cc}\sin \left(k(a+\delta )\right)& \cos \left(k(a+\delta )\right)\\ \cos \left(k(a+\delta )\right)& -\sin \left(k(a+\delta )\right)\end{array}\right)\left(\begin{array}{c}{A}_3\\ B_3\end{array}\right)\\ \left(\begin{array}{c}{A}_5\\ B_5\end{array}\right)={\left(\begin{array}{cc}0& 1\\ 1& -\frac{\alpha }{k}\end{array}\right)}^{-1}\left(\begin{array}{cc}\sin \left(k(a-\delta )\right)& \cos \left(k(a-\delta )\right)\\ \cos \left(k(a-\delta )\right)& -\sin \left(k(a-\delta )\right)\end{array}\right)\left(\begin{array}{c}{A}_4\\ B_4\end{array}\right)\end{array}}$

El coeficiente A₁ se determina de modo que la suma

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{a}{\int }}{\left(A_1\sin \left(kx\right)+B_1\cos \left(kx\right)\right)}^{2}dx}+\\ {\displaystyle \underset{a}{\overset{2a}{\int }}{\left(A_2\sin \left(k(x-a)\right)+B_2\cos \left(k(x-a)\right)\right)}^{2}dx}+\\ {\displaystyle \underset{2a}{\overset{3a+\delta }{\int }}{\left(A_3\sin \left(k(x-2a)\right)+B_3\cos \left(k(x-2a)\right)\right)}^{2}dx}+\\ {\displaystyle \underset{3a+\delta }{\overset{4a}{\int }}{\left(A_4\sin \left(k(x-3a-\delta )\right)+B_4\cos \left(k(x-3a-\delta )\right)\right)}^{2}dx}+\\ {\displaystyle \underset{4a}{\overset{5a}{\int }}{\left(A_5\sin \left(k(x-4a)\right)+B_5\cos \left(k(x-4a)\right)\right)}^{2}dx}=1\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}\frac{A_1^2}{2}\left(a-\frac{\sin (2ka)}{2k}\right)+\frac{B_1^2}{2}\left(a+\frac{\sin (2ka)}{2k}\right)-\frac{A_1{B}_1}{2k}\left(\cos (2ka)-1\right)+\\ \frac{A_2^2}{2}\left(a-\frac{\sin (2ka)}{2k}\right)+\frac{B_2^2}{2}\left(a+\frac{\sin (2ka)}{2k}\right)-\frac{A_2{B}_2}{2k}\left(\cos (2ka)-1\right)+\\ \frac{A_3^2}{2}\left(a+\delta -\frac{\sin \left(2k(a+\delta )\right)}{2k}\right)+\frac{B_3^2}{2}\left(a+\delta +\frac{\sin \left(2k(a+\delta )\right)}{2k}\right)-\frac{A_3{B}_3}{2k}\left(\cos \left(2k(a+\delta )\right)-1\right)+\\ \frac{A_4^2}{2}\left(a-\delta -\frac{\sin \left(2k(a-\delta )\right)}{2k}\right)+\frac{B_4^2}{2}\left(a-\delta +\frac{\sin \left(2k(a-\delta )\right)}{2k}\right)-\frac{A_4{B}_4}{2k}\left(\cos \left(2k(a-\delta )\right)-1\right)+\\ \frac{A_5^2}{2}\left(a-\frac{\sin (2ka)}{2k}\right)+\frac{B_5^2}{2}\left(a+\frac{\sin (2ka)}{2k}\right)-\frac{A_5{B}_5}{2k}\left(\cos (2ka)-1\right)=1\end{array}}$

Representamos las funciones de onda correspondientes a los dos primeros niveles de energía para un sistama de N=4 potenciales delta de Dirac, fijamos la separación constante a=1, el parámetro α=2, de todos los potenciales. El tercero, n=3, se desplaza δ=0.75

function delta_dirac_28
    a=1;
    alfa=2;
    delta=0.75;
    N=4;
    n=3; %posición defecto
    ff=@(x) niveles(x);
    xb=buscar_intervalos(ff,0.1,4,50);
    nb=size(xb);
    kn=zeros(1,nb(1));
    for m=1:nb(1)
        kn(m)=fzero(ff,[xb(m,1) xb(m,2)]);
    end
    disp(kn)

    A=zeros(1,N+1);
    B=zeros(1,N+1);
    A(1)=1; B(1)=0;
    for k=kn(1:2)
        NI=[alfa/k,1;1,0];  
        M=[sin(k*a),cos(k*a);cos(k*a),-sin(k*a)];
        Ma=[sin(k*(a+delta)),cos(k*(a+delta));cos(k*(a+delta)),
-sin(k*(a+delta))];
        Mb=[sin(k*(a-delta)),cos(k*(a-delta));cos(k*(a-delta)),
-sin(k*(a-delta))];
        suma=A(1)^2*(a-sin(2*k*a)/(2*k))/2+B(1)^2*(a+sin(2*k*a)/(2*k))/2
-A(1)*B(1)*(cos(2*k*a)-1)/(2*k);
        for m=1:n-1
            Z=(NI*M)*[A(m);B(m)];
            A(m+1)=Z(1);
            B(m+1)=Z(2);
            suma=suma+A(m+1)^2*(a-sin(2*k*a)/(2*k))/2+B(m+1)^2*(a+sin(2*k*a)
/(2*k))/2-A(m+1)*B(m+1)*(cos(2*k*a)-1)/(2*k);
        end
        suma=suma+A(m+1)^2*(a+delta-sin(2*k*(a+delta))/(2*k))/2+B(m+1)^2*
(a+delta+sin(2*k*(a+delta))/(2*k))/2-A(m+1)*B(m+1)*(cos(2*k*(a+delta))-1)
/(2*k);
        m=n;
        Z=(NI*Ma)*[A(m);B(m)];
        A(m+1)=Z(1);
        B(m+1)=Z(2);
        suma=suma+A(m+1)^2*(a-delta-sin(2*k*(a-delta))/(2*k))/2+B(m+1)^2*
(a-delta+sin(2*k*(a-delta))/(2*k))/2-A(m+1)*B(m+1)*(cos(2*k*(a-delta))-1)
/(2*k);       
        m=n+1;
        Z=(NI*Mb)*[A(m);B(m)];
        A(m+1)=Z(1);
        B(m+1)=Z(2);
        suma=suma+A(m+1)^2*(a-sin(2*k*a)/(2*k))/2+B(m+1)^2*(a+sin(2*k*a)
        /(2*k))/2-A(m+1)*B(m+1)*(cos(2*k*a)-1)/(2*k);
        
        for m=n+2:N
            Z=(NI*M)*[A(m);B(m)];
            A(m+1)=Z(1);
            B(m+1)=Z(2);
            suma=suma+A(m+1)^2*(a-sin(2*k*a)/(2*k))/2+B(m+1)^2*(a+sin(2*k*a)
            /(2*k))/2-A(m+1)*B(m+1)*(cos(2*k*a)-1)/(2*k);
        end
        hold on
        for m=0:n-2
            fplot(@(x) (A(m+1)*sin(k*(x-m*a))+B(m+1)*cos(k*(x-m*a)))/
sqrt(suma),[m*a,(m+1)*a])
        end
        m=n-1;
        fplot(@(x) (A(m+1)*sin(k*(x-m*a))+B(m+1)*cos(k*(x-m*a)))/
sqrt(suma),[m*a,(m+1)*a+delta])
        m=n;
        fplot(@(x) (A(m+1)*sin(k*(x-m*a-delta))+B(m+1)*cos(k*(x-m*a-delta)))
/sqrt(suma),[m*a+delta,(m+1)*a])
        for m=n+1:N
            fplot(@(x) (A(m+1)*sin(k*(x-m*a))+B(m+1)*cos(k*(x-m*a)))
/sqrt(suma),[m*a,(m+1)*a])
        end
     end
    hold off
    grid on
    xlabel('x')
    ylabel('\Phi(x)')
    title('Funciones de onda')


    function res=niveles(k)
        T=eye(2);
        M=[0,1; 1,-alfa/k];  
        MI=[sin(k*a),cos(k*a);cos(k*a),-sin(k*a)];
       MIa=[sin(k*(a+delta)),cos(k*(a+delta));cos(k*(a+delta)),-sin(k*(a+delta))];
       MIb=[sin(k*(a-delta)),cos(k*(a-delta));cos(k*(a-delta)),-sin(k*(a-delta))];
       for s=N:-1:n+2
             T=(MI*M)*T;
       end
        T=(MIb*M)*T;
        T=(MIa*M)*T;
       for s=n-1:-1:1
             T=(MI*M)*T;
       end
        res=T(2,1)*cos(k*a)-T(2,2)*sin(k*a);
    end

   function xb = buscar_intervalos(f,a,b,n)
        x = a:(b-a)/n:b;
        j = 0; 
        y1=f(x(1));
        xb=[];
        for i = 1:length(x)-1
            y2=f(x(i+1));
            if sign(y1) ~= sign(y2) 
                j = j + 1;
                xb(j,1) = x(i);
                xb(j,2) = x(i+1);
            end
            y1=y2;
        end
        if isempty(xb) 
            disp('no se han encontrado cambios de signo')
        else
            disp(['número de intervalos:' int2str(j)]) 
        end
    end
end

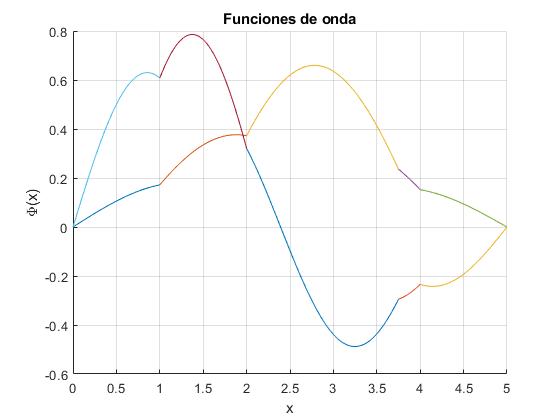
Las primeras raíces k de la ecuación transcendente son

 1.2432    1.8356    2.3518    2.7170    3.1965

Referencias

Todd K. Timberlake, Neilson Woodfield. Band formation and defects in a finite periodic quantum potential. Am. J. Phys. 90 (2), February 2022. pp. 93-102