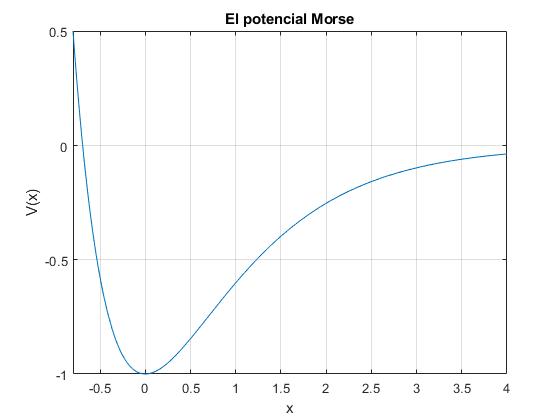
El potencial de Morse

${\displaystyle V(r)=D\exp \left(-2\alpha (r-r_0)\right)-2D\exp \left(-\alpha (r-r_0)\right)}$

Donde r es la distancia entre los átomos, r₀ es la distancia de equilibrio, D es la profundidad del pozo y α es una variable que controla el ancho del potencial.

En esta sección, resolveremos la ecuación de Schrödinger independiente del tiempo en una región unidimensional cuya energía potencial viene descrita por la función V(x)

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}\frac{d^2\psi (x)}{d{x}^2}+V(x)·\psi (x)=E·\psi (x)\\ V(x)=D{e}^{-2\alpha x}-2D{e}^{-\alpha x}\end{array}}$

alfa=1;
D=1;
fplot(@(x) D*exp(-2*alfa*x)-2*D*exp(-alfa*x), [-0.8,4])
grid on
xlabel('x')
ylabel('V(x)');
title('El potencial Morse')

Modificar el valor de la variable alfa a 0.75 y a 1.5 para ver el efecto

Hacemos el cambio de variable y=exp(-αx)

${\displaystyle \begin{array}{l}\frac{d\psi }{dx}=\frac{d\psi }{dy}\frac{dy}{dx}=-\alpha \frac{d\psi }{dy}{e}^{-\alpha x}=-\alpha \frac{d\psi }{dy}y\\ \frac{d^2\psi }{d{x}^2}=\frac{d}{dx}\left(\frac{d\psi }{dx}\right)=\frac{d}{dy}\left(-\alpha \frac{d\psi }{dy}y\right)\frac{dy}{dx}={\alpha }^2{e}^{-\alpha x}\frac{d}{dy}\left(\frac{d\psi }{dy}y\right)={\alpha }^{2}y\left(\frac{d^2\psi }{d{y}^2}y+\frac{d\psi }{dy}\right)\end{array}}$

La ecuación diferencial se transforma en

${\displaystyle \frac{d^2\psi }{d{y}^2}+\frac{1}{y}\frac{d\psi }{dy}+\frac{2m}{{\hslash }^2{\alpha }^2}\left(\frac{2D}{y}-D+\frac{E}{y^2}\right)\psi =0}$

Hacemos un nuevo cambio de variable, z=2yλ

${\displaystyle \frac{d^2\psi }{d{z}^2}+\frac{1}{z}\frac{d\psi }{dz}+\frac{2m}{{\hslash }^2{\alpha }^2}\left(\frac{D}{z\lambda }-\frac{D}{4{\lambda }^2}+\frac{E}{z^2}\right)\psi =0}$

Finalmente, hacemos un cambio de variable similar al efectuado para encontrar la solución de la ecuación radial del átomo de hidrógeno

${\displaystyle \begin{array}{l}\psi =e^{-z/2}{z}^{b/2}F(z)\\ \lambda =\frac{\sqrt{2mD}}{\alpha \hslash },b^2=-\frac{8mE}{{\alpha }^2{\hslash }^2}\end{array}}$

Las derivadas primera y segunda de ψ son

${\displaystyle \begin{array}{l}\psi =e^{-z/2}{z}^{b/2}F(z)\\ \frac{d\psi }{dz}=-\frac{1}{2}{e}^{-z/2}{z}^{b/2}F+\frac{b}{2}{e}^{-z/2}{z}^{b/2-1}F+e^{-z/2}{z}^{b/2}\frac{dF}{dz}\\ \frac{d^2\psi }{d{z}^2}=\left\{\begin{array}{l}\frac{1}{4}{e}^{-z/2}{z}^{b/2}F-\frac{b}{4}{e}^{-z/2}{z}^{b/2-1}F-\frac{1}{2}{e}^{-z/2}{z}^{b/2}\frac{dF}{dz}+\\ -\frac{b}{4}{e}^{-z/2}{z}^{b/2-1}F+\frac{b}{2}\left(\frac{b}{2}-1\right)e^{-z/2}{z}^{b/2-2}F+\frac{b}{2}{e}^{-z/2}{z}^{b/2-1}\frac{dF}{dz}+\\ -\frac{1}{2}{e}^{-z/2}{z}^{b/2}\frac{dF}{dz}+\frac{b}{2}{e}^{-z/2}{z}^{b/2-1}\frac{dF}{dz}+e^{-z/2}{z}^{b/2}\frac{d^{2}F}{d{z}^2}\end{array}\right\}\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}\frac{d^2\psi }{d{z}^2}+\frac{1}{z}\frac{d\psi }{dz}+\left(\frac{2mD}{{\hslash }^2{\alpha }^2\lambda }\frac{1}{z}-\frac{1}{4}-\frac{b^2}{4z^2}\right)\psi =0\\ \left(e^{-z/2}{z}^{b/2-1}\right)\left\{z\frac{d^{2}F}{d{z}^2}+\left(-z+b+1\right)\frac{dF}{dz}+\left(\frac{z}{4}-\frac{b}{2}+\frac{b^2}{4z}-\frac{1}{2}+\left(\lambda -\frac{z}{4}-\frac{b^2}{4z}\right)\right)F\right\}=0\end{array}}$

Simplificando, obtenemos la ecuación diferencial cuya solución son los polinomios asociados de Laguerre, de modo similar a la ecuación radial del átomo de hidrógeno

${\displaystyle z\frac{d^{2}F}{d{z}^2}+\left(-z+b+1\right)\frac{dF}{dz}+\left(\lambda -\frac{b}{2}-\frac{1}{2}\right)F=0}$

La ecuación diferencial y su solución, los polinomios asociados de Laguerre son

${\displaystyle \begin{array}{l}x\frac{d^{2}y}{d{x}^2}+\left(m+1-x\right)\frac{dy}{dx}+ny=0\\ L_n^m(x)=(n+m)!{\displaystyle \sum _{k=0}^n\frac{{\left(-1\right)}^k}{(n-k)!(k+m)!k!}{x}^k}\end{array}}$

Comparando ambas ecuaciones, m=b

${\displaystyle \begin{array}{l}\lambda -\frac{b}{2}-\frac{1}{2}=n\\ b=2\lambda -1-2n\end{array}}$

n es un número entero mayor o igual que cero. Los valores de b deberán ser positivos, por lo que n está limitado

${\displaystyle 2\lambda -1-2n\ge \mathrm{0,}n\le \lambda -\frac{1}{2}}$

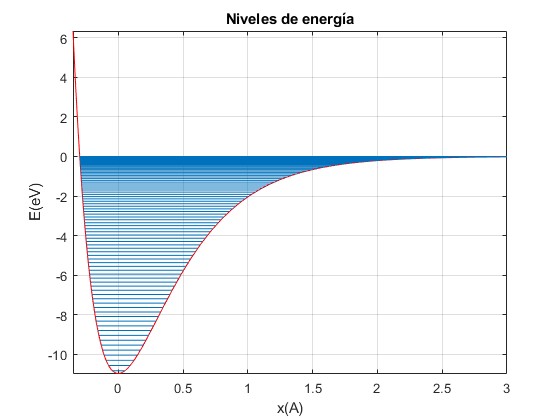
Niveles de energía

Conocido b, despejamos la energía E

${\displaystyle \begin{array}{l}{E}_n=-\frac{{\alpha }^2{\hslash }^2}{8m}{\left(2\frac{\sqrt{2mD}}{\alpha \hslash }-1-2n\right)}^2=-\frac{{\alpha }^2{\hslash }^2}{8m}\left(\frac{8mD}{{\alpha }^2{\hslash }^2}+1+4n^2-4\frac{\sqrt{2mD}}{\alpha \hslash }-8\frac{\sqrt{2mD}}{\alpha \hslash }n+4n\right)=\\ -D+\frac{{\alpha }^2{\hslash }^2}{m}\frac{\sqrt{2mD}}{\alpha \hslash }\left(n+\frac{1}{2}\right)-\frac{{\alpha }^2{\hslash }^2}{8m}{\left(1+2n\right)}^2\\ E_n=-D+\alpha \hslash \sqrt{\frac{2D}{m}}\left(n+\frac{1}{2}\right)-\frac{{\alpha }^2{\hslash }^2}{2m}{\left(n+\frac{1}{2}\right)}^2\end{array}}$

Sea una molécula de CO. Los datos son

• Masa del Carbono, 12.0115, amu
• Masa del Oxígeno, 15.994, amu
• Parámetro D=10.970, eV
• Parámetro α=2.325, Å^-1

La masa reducida m=m₁·m₂/(m₁+m₂)=6.8608 amu

Los puntos de intersección de la recta y=E y la función potencial y=Dexp(-2αx)-2Dexp(-αx) se han calculado en la página titulada el El potencial de Morse

${\displaystyle x_{\mathrm{1,2}}=-\frac{1}{\alpha }\ln \left(1\pm \sqrt{\frac{E+D}{D}}\right)}$

mC=12.0115; %amu
mO=15.9994;
m=mO*mC*1.6604e-27/(mO+mC); %masa reducida, kg
D=10.970; %eV
alfa=2.325; %A^-1
h=1.0545e-34; %h/(2*pi)
lambda=sqrt(2*m*D*1.6e-19)/(alfa*1e10*h);

n=0:lambda-1/2;
E=(-D*1.6e-19+alfa*1e10*h*sqrt(2*D*1.6e-19/m)*(n+1/2)-
(alfa*1e10*h)^2*(n+1/2).^2/(2*m))/1.6e-19 %en eV
fplot(@(x) D*exp(-2*alfa*x)-2*D*exp(-alfa*x),[-0.35,3], 'color','r')
for k=0:length(E)
    x1=-log(1+sqrt((E(k)+D)/D))/alfa;
    x2=-log(1-sqrt((E(k)+D)/D))/alfa;
   line([x1,x2],[E(k), E(k)])
end
grid on
xlim([-0.35,3])
xlabel('x(A)')
ylabel('E(eV)')
title('Niveles de energía')

La separación entre los niveles va disminuyendo a medida que aumenta el ancho de la función potencial

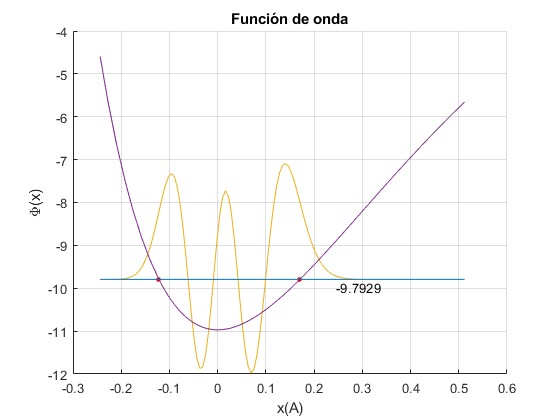
Funciones de onda

${\displaystyle \psi (z)=C{e}^{-z/2}{z}^{b/2}{L}_n^b(z)}$

La constante C se calcula de modo que

${\displaystyle \begin{array}{l}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\left|\psi (z)\right|}^{2}dz}=1\\ C^2{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{e}^{-z}{z}^b{\left(L_n^b(z)\right)}^{2}dz}=1\end{array}}$

Las funciones de onda correspondientes a los niveles de energía n=0, 1,2,3...λ-1/2, son

${\displaystyle \begin{array}{l}{\psi }_n(z)=C\exp \left(-\frac{z}{2}\right)z^{\lambda -n-1/2}{L}_n^{2\lambda -2n-1}(z)\\ z=2\lambda y=2\lambda \exp (-\alpha x)\end{array}}$

Existe una expresión analítica para el coeficiente C pero no se incluye porque difiere del valor de de C calculado a partir de la integral del cuadrado de la función de onda entre -∞ e ∞

Seleccionamos la función de onda que queremos representar correspondiente al nivel de energía n=0, 1,2,3...λ-1/2

Los puntos de color rojo, señalan las posiciones x₁ y x₂ intersección de la energía potencial V(x) con el nivel de energía E_n considerado. La función de onda decrece rápidamente hacia la izquierda o hacia la derecha de dichas posiciones, como apreciamos en la figura

En la parte derecha, se porporciona la energía del nivel en eV

function morse_9
    mC=12.0115; %amu
    mO=15.9994;
    m=mO*mC*1.6604e-27/(mO+mC); %kg
    D=10.970; %eV
    alfa=2.325; %A^-1
    h=1.0545e-34; %h/(2*pi)
    lambda=sqrt(2*m*D*1.6e-19)/(alfa*1e10*h);
    f=@(x) D*exp(-2*alfa*x)-2*D*exp(-alfa*x); %en eV

    n=2; %numero de nivel (cambiar)
    E=(-D*1.6e-19+alfa*1e10*h*sqrt(2*D*1.6e-19/m)*(n+1/2)-
(alfa*1e10*h)^2*(n+1/2).^2/(2*m))/1.6e-19; %en eV
    x1=-log(1+sqrt((E+D)/D))/alfa;
    x2=-log(1-sqrt((E+D)/D))/alfa;
    hold on
    plot(x1,E,'ro','markersize',3,'markerfacecolor','r')
    plot(x2,E,'ro','markersize',3,'markerfacecolor','r')
    text(2*x2, E,num2str(E),'VerticalAlignment','top',
'HorizontalAlignment','right');
    g=@(x) fOnda(n,x).^2;
    c2=integral(g,3*x1,5*x2);
    x=linspace(2*x1,2*x2,100);
    y=E+fOnda(n,x)/sqrt(c2); %normaliza
    plot(x,y)
   fplot(f, [2*x1,3*x2])
   line([2*x1,3*x2],[E,E])
    hold off
    grid on
    xlabel('x(A)')
    ylabel('\Phi(x)')
    title('Función de onda')
    
    function res=fOnda(n,x)
        m=round(2*lambda-2*n-1);
        z=2*lambda*exp(-alfa*x);
        res=exp(-z/2).*z.^(m/2).*laguerreL(n,m,z);
    end
    
end

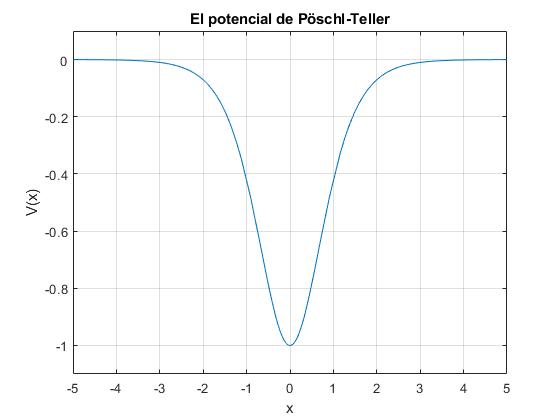
El potencial de Pöschl–Teller

En esta sección, resolveremos la ecuación de Schrödinger independiente del tiempo en una región unidimensional cuya energía potencial viene descrita por la función V(x). Se trata de una versión reducida del potencial de Pöschl–Teller

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}\frac{d^2\psi (x)}{d{x}^2}+V(x)·\psi (x)=E·\psi (x)\\ V(x)=-\frac{\lambda (\lambda +1)}{2}\frac{1}{{\cosh }^2(x)}\end{array}}$

λ es un parámetro que controla la profundidad del pozo de potencial

lambda=1;
fplot(@(x) -lambda*(lambda+1)./(2*cosh(x).^2), [-5,5])
grid on
ylim([-1.1,0.1])
xlabel('x')
ylabel('V(x)');
title('El potencial de Pöschl-Teller')

Establecemos un sistema de unidades en el que ℏ=m=1

${\displaystyle \frac{d^2\psi (x)}{d{x}^2}+\left(\frac{\lambda (\lambda +1)}{{\cosh }^2(x)}+2E\right)\psi (x)=0}$

Hacemos el cambio de variable z=tanhx

${\displaystyle \begin{array}{l}\frac{d\psi }{dx}=\frac{d\psi }{dz}\frac{dz}{dx}=\frac{d\psi }{dz}\frac{1}{{\cosh }^{2}x}=\frac{d\psi }{dz}\left(1-{\tanh }^{2}x\right)=\frac{d\psi }{dz}\left(1-z^2\right)\\ \frac{d^2\psi }{d{x}^2}=\frac{d}{dx}\left(\frac{d\psi }{dx}\right)=\frac{d}{dz}\left(\frac{d\psi }{dz}\left(1-z^2\right)\right)\frac{dz}{dx}=\left(\left(1-z^2\right)\frac{d^2\psi }{d{z}^2}-2z\frac{d\psi }{dz}\right)\left(1-z^2\right)\end{array}}$

El resultado es

${\displaystyle \left(1-z^2\right)\frac{d^2\psi }{d{z}^2}-2z\frac{d\psi }{dz}+\left(\lambda (\lambda +1)+\frac{2E}{1-z^2}\right)\psi =0}$

Los polinomios asociados de Legendre, $P_n^m(x)$, satisfacen la ecuación diferencial

${\displaystyle \begin{array}{l}\left(1-x^2\right)\frac{d^{2}y}{d{x}^2}-2x\frac{dy}{dx}+\left(n(n+1)-\frac{m^2}{1-x^2}\right)y=0\\ y=P_n^m(x)=\mathrm{0,}m>n\end{array}}$

Niveles de energía

Identificamos n=λ. Los niveles de energía son

${\displaystyle E_{\lambda ,m}=-\frac{m^2}{2},m=\mathrm{1,2,3...}\lambda }$

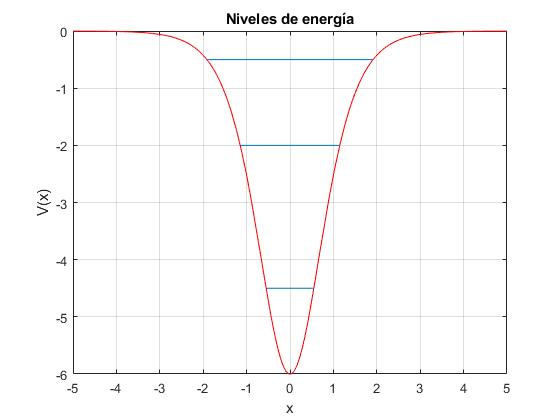
Los puntos de intersección de la recta y=E y la función potencial y=V(x) son simétricos respecto del origen

${\displaystyle x_{\mathrm{1,2}}=\pm \text{arccosh}\left(\sqrt{-\frac{\lambda (\lambda +1)}{2E}}\right)}$

Representamos los niveles de energía para λ=3

lambda=3;
fplot(@(x) -lambda*(lambda+1)./(2*cosh(x).^2), [-5,5], 'color','r')
for m=1:lambda
    E=-m^2/2;
    x1=acosh(sqrt(-lambda*(lambda+1)/(2*E)));
    line([-x1,x1],[E,E])
end
grid on
xlabel('x')
ylabel('V(x)');
title('Niveles de energía')

Funciones de onda

Funciones de onda son los polinomios asociados de Laguerre

${\displaystyle {\psi }_{\lambda }^m(x)=P_{\lambda }^m\left(\tanh x\right),m=\mathrm{1,2,3...}\lambda }$

syms x;
for n=1:4
    for m=1:n
        y=(1-x^2)^(m/2)*diff(legendreP(n,x),m);
        disp([n,m])
        y=simplify(y)
    end
end

      1     1    y =(1 - x^2)^(1/2)
      2     1    y =3*x*(1 - x^2)^(1/2)
      2     2    y =3 - 3*x^2
      3     1    y =(1 - x^2)^(1/2)*((15*x^2)/2 - 3/2)
      3     2    y =-15*x*(x^2 - 1)
      3     3    y =15*(1 - x^2)^(3/2)
      4     1    y =(5*x*(1 - x^2)^(1/2)*(7*x^2 - 3))/2
      4     2    y =-(x^2 - 1)*((105*x^2)/2 - 15/2)
      4     3    y =105*x*(1 - x^2)^(3/2)
      4     4    y =105*(x^2 - 1)^2

Sustituimos x por tanhx mediante el comando subs y simplificamos con simplify

syms x;
for n=1:4
    for m=1:n
        y=(1-x^2)^(m/2)*diff(legendreP(n,x),m);
        disp([n,m])
        y=simplify(y);
        y=subs(y,{x},{tanh(x)});
        y=simplify(y)
    end
end

Probamos el código, vemos que no se simplifican las expresiones algebraicas, por lo que lo decidimos hacerlo a mano

${\displaystyle \begin{array}{l}{\psi }_1^1(x)=\sqrt{\left(1-{\tanh }^2(x)\right)}=\frac{1}{\cosh (x)}\\ {\psi }_2^1(x)=3\tanh (x)\sqrt{\left(1-{\tanh }^2(x)\right)}=3\frac{\tanh (x)}{\cosh (x)}\\ {\psi }_2^2(x)=3\left(1-{\tanh }^2(x)\right)=\frac{3}{{\cosh }^2(x)}\\ {\psi }_3^1(x)=\frac{3}{2}(5{\tanh }^2(x)-1)\sqrt{\left(1-{\tanh }^2(x)\right)}=\frac{3}{2}\frac{5{\tanh }^2(x)-1}{\cosh (x)}\\ {\psi }_3^2(x)=15\tanh (x)\left(1-{\tanh }^2(x)\right)=15\frac{\tanh (x)}{{\cosh }^2(x)}\\ {\psi }_3^3(x)=15{\left(1-{\tanh }^2(x)\right)}^{3/2}=\frac{15}{{\cosh }^3(x)}\\ {\psi }_4^1(x)=\frac{5}{2}\frac{\tanh (x)}{\cosh (x)}\left(7{\tanh }^2(x)-3\right)\\ {\psi }_4^2(x)=\frac{15}{2}\frac{7{\tanh }^2(x)-1}{{\cosh }^2(x)}\\ {\psi }_4^3(x)=105\frac{\tanh (x)}{{\cosh }^3(x)}\\ {\psi }_4^4(x)=105\frac{1}{{\cosh }^4(x)}\end{array}}$

Representamos las funciones de onda de cada uno de los tres niveles de energía correspondientes a λ=3

Antes de representarlos, hay que calcular el coeficiente C que multiplica a la función de onda ${\psi }_{\lambda }^m(x)$ tal que

${\displaystyle {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{\left|\psi (x)\right|}^{2}dx}=1}$

Como las funciones de onda son simétricas o antisimétricas, basta calcular la integral entre 0 e ∞ y multiplicar por dos

lambda=3;
f={@(x) (5*tanh(x).^2-1)./cosh(x), @(x) tanh(x)./cosh(x).^2, @(x) 1./cosh(x).^3};
hold on
for m=1:lambda
    E=-m^2/2;
    x1=acosh(sqrt(-lambda*(lambda+1)/(2*E)));
    C=sqrt(0.5/integral(f{m},0,5*x1));
    g=@(x) C*f{m}(x);
    fplot(g, [-4*x1, 4*x1],'displayName',num2str(E))
end
hold off
grid on
legend('-DynamicLegend','location','best')
xlabel('x')
ylabel('V(x)');
title('Niveles de energía')

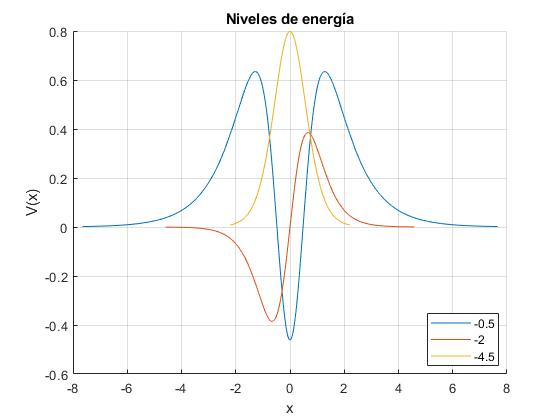
En la parte inferior derecha, se muestra en valor de la energía de cada uno de los tres niveles

Referencias

Philip M. Morse. Diatomic molecules according to the Wave Mechanics. II. Vibrational levels. Physical Review. Volume 34, July 1, 1929, pp. 57-64

Erin Brown, Lisandro Hernández de la Peña. A Simplified Pöschl−Teller Potential: An Instructive Exercise for Introductory Quantum Mechanics. Journal of Chemical Education. DOI:10.1021/acs.jchemed.8b00029