Sistema de pozos de potencial

Consideremos un sistema de N pozos de potencial iguales de anchura a separados por barreras de potencial de anchura b y altura V₀. Establecemos el origen en el centro del sistema. El eje vertical puede coincidir en medio de un pozo si el número de pozos N es impar, tal como muestra la figura o bien, coincidir en medio de una barrera si el número de pozos N es par

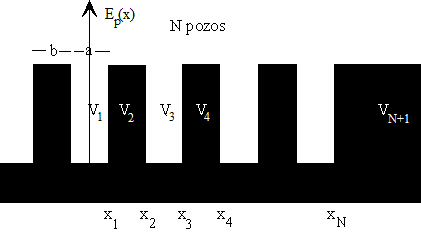
Resolviendo la ecuación de Schrödinger en cada una de las regiones tenemos.

$Ψ_{j} (x) = A_{j} \exp (i q_{j} x) + B_{j} \exp (- i q_{j} x) q_{j}^{2} = \frac{2 m (E - V_{j})}{ℏ^{2}} j = 1, ... N + 1$

donde q_j es un número complejo real o imaginario dependiendo si la región es un pozo V_j=0 o una barrera E<V_j.

En las fronteras entre las regiones hemos de aplicar las condiciones de continuidad de la función de onda y de su derivada primera. Sea la frontera entre las regiones j-1 y j, cuya abscisa es x_j.

$\begin{array}{l} A_{j - 1} \exp (i q_{j - 1} x_{j}) + B_{j - 1} \exp (- i q_{j - 1} x_{j}) = A_{j} \exp (i q_{j} x_{j}) + B_{j} \exp (- i q_{j} x_{j}) \\ q_{j - 1} (A_{j - 1} \exp (i q_{j - 1} x_{j}) - B_{j - 1} \exp (- i q_{j - 1} x_{j})) = q_{j} (A_{j} \exp (i q_{j} x_{j}) - B_{j} \exp (- i q_{j} x_{j})) \end{array}$

que relaciona coeficientes A_j y B_j con A_j-1 y B_j-1

Tenemos un sistema de 2N ecuaciones con 2N+2 incógnitas. Ahora bien, el número de incógnitas se reduce teniendo en cuenta la simetría de la función potencial y la definición de función de onda:

En la región N+1, la función de onda Ψ_N+1(x) tiende a cero al hacerse x grande, de modo que al ser q_N+1 imaginario, el coeficiente B_N+1 debe de ser cero.

En la primera región de potencial la función de onda es

$Ψ_{1} (x) = A_{1} \exp (i q_{1} x) + B_{1} \exp (- i q_{1} x)$

Las funciones de onda simétricas son aquellas que

$Ψ (x) = Ψ (- x) A_{1} = B_{1}$

Las funciones de onda antisimétricas son aquellas que

$Ψ (x) = - Ψ (- x) A_{1} = - B_{1}$

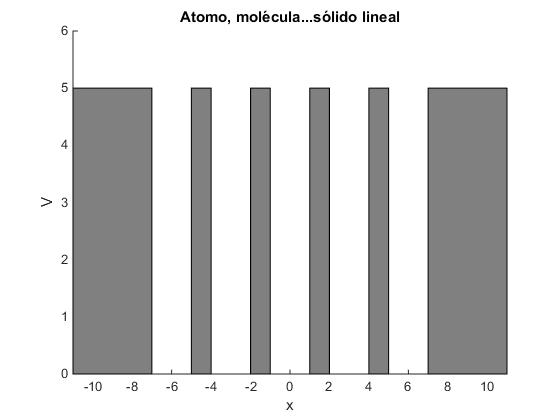
Potencial

Sea un sistema formado por N=5 pozos de potencial

x₁=a/2, x₂=a/2+b, x₃=3a/2+b, x₄=3a/2+2b, x₅=5a/2+2b

V₁=0, V₁=V₀, V₃=0, V₄=V₀, V₅=0, V₆=V₀

Elaboramos un script para representar el potencial. Se presentan dos casos: cuando el número de pozos N es par (la barrera está en el origen) o impar (el pozo está en el origen)

a=2;  %anchura del pozo
b=1; %separación entre pozos
N=5; %número de pozos
H=5.0; %altura del pozo

x=zeros(N+1,1);
V=zeros(N+1,1);
if rem(N,2)==0
    V(1)=H;
    x(1)=b/2;
    for i=2:2:N-1
        x(i)=x(i-1)+a;
        V(i)=0;
        x(i+1)=x(i)+b;
        V(i+1)=H;
    end
    x(N)=x(N-1)+a;
else
    x(1)=a/2;
    V(1)=0;
    for i=2:2:N
        x(i)=x(i-1)+b;
        V(i)=H;
        x(i+1)=x(i)+a;
        V(i+1)=0;
    end
 end
x(N+1)=x(N)+2*a;
V(N+1)=H;
%dibuja el potencial periódico

if rem(N,2)==0
    fill([-x(1) -x(1) x(1) x(1)],[0 V(1) V(1) 0],[0.5 0.5 0.5])
    for i=2:2:N-1
        fill([x(i) x(i) x(i+1) x(i+1)],[0 V(i+1) V(i+1) 0],
[0.5 0.5 0.5])
        fill([-x(i) -x(i) -x(i+1) -x(i+1)],[0 V(i+1) V(i+1) 0],
[0.5 0.5 0.5])
    end
else
    for i=1:2:N-1
        fill([x(i) x(i) x(i+1) x(i+1)],[0 V(i+1) V(i+1) 0],
[0.5 0.5 0.5])
        fill([-x(i) -x(i) -x(i+1) -x(i+1)],[0 V(i+1) V(i+1) 0],
[0.5 0.5 0.5])
    end
end
fill([x(N) x(N) x(N+1) x(N+1)],[0 V(N+1) V(N+1) 0],[0.5 0.5 0.5])
fill([-x(N) -x(N) -x(N+1) -x(N+1)],[0 V(N+1) V(N+1) 0],[0.5 0.5 0.5])
...

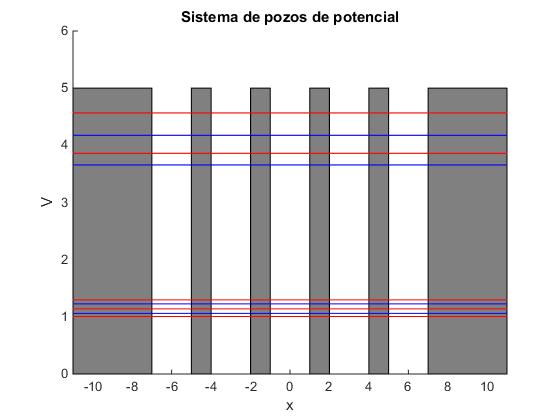
Niveles de energía

Para que sea función de onda, B₆=0. Aplicamos las condiciones de continuidad en los puntos x₁, x₂, ... x₅

$\begin{array}{l} x_{1} {\begin{cases} A_{1} \exp (i q_{1} x_{1}) + B_{1} \exp (- i q_{1} x_{1}) = A_{2} \exp (i q_{2} x_{1}) + B_{2} \exp (- i q_{2} x_{1}) \\ A_{1} q_{1} \exp (i q_{1} x_{1}) - B_{1} q_{1} \exp (- i q_{1} x_{1}) = A_{2} q_{2} \exp (i q_{2} x_{1}) - B_{2} q_{2} \exp (- i q_{2} x_{1}) \end{cases} \\ x_{2} {\begin{cases} A_{2} \exp (i q_{2} x_{2}) + B_{2} \exp (- i q_{2} x_{2}) = A_{3} \exp (i q_{3} x_{2}) + B_{3} \exp (- i q_{3} x_{2}) \\ A_{2} q_{2} \exp (i q_{2} x_{2}) - B_{2} q_{2} \exp (- i q_{2} x_{2}) = A_{3} q_{3} \exp (i q_{3} x_{2}) - B_{3} q_{3} \exp (- i q_{3} x_{2}) \end{cases} \\ x_{3} {\begin{cases} A_{3} \exp (i q_{3} x_{3}) + B_{3} \exp (- i q_{3} x_{3}) = A_{4} \exp (i q_{4} x_{3}) + B_{4} \exp (- i q_{4} x_{3}) \\ A_{3} q_{3} \exp (i q_{3} x_{3}) - B_{3} q_{3} \exp (- i q_{3} x_{3}) = A_{4} q_{4} \exp (i q_{4} x_{3}) - B_{4} q_{4} \exp (- i q_{4} x_{3}) \end{cases} \\ x_{4} {\begin{cases} A_{4} \exp (i q_{4} x_{4}) + B_{4} \exp (- i q_{4} x_{4}) = A_{5} \exp (i q_{5} x_{4}) + B_{5} \exp (- i q_{5} x_{4}) \\ A_{4} q_{4} \exp (i q_{4} x_{4}) - B_{4} q_{4} \exp (- i q_{4} x_{4}) = A_{5} q_{5} \exp (i q_{5} x_{4}) - B_{5} q_{5} \exp (- i q_{5} x_{4}) \end{cases} \\ x_{5} {\begin{cases} A_{5} \exp (i q_{5} x_{5}) + B_{5} \exp (- i q_{5} x_{5}) = A_{6} \exp (i q_{6} x_{5}) \\ A_{5} q_{5} \exp (i q_{5} x_{5}) - B_{5} q_{5} \exp (- i q_{5} x_{5}) = A_{6} q_{6} \exp (i q_{6} x_{5}) \end{cases} \end{array}$

Para las funciones de onda simétricas, A₁=B₁
Para las funciones de onda antisimétricas, A₁=-B₁

En ambos casos, tenemos un sistema homogéneo de 2N ecuaciones con 2N incógnitas. El determinante de la matriz de los coeficientes deberá ser cero. De este modo, buscamos los niveles de energía

$(\begin{matrix} e^{i q_{1} x_{1}} \pm e^{- i q_{1} x_{1}} & - e^{i q_{2} x_{1}} & - e^{- i q_{2} x_{1}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ q_{1} (e^{i q_{1} x_{1}} \mp e^{- i q_{1} x_{1}}) & - q_{2} e^{i q_{2} x_{1}} & q_{2} e^{- i q_{2} x_{1}} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & e^{i q_{2} x_{2}} & e^{- i q_{2} x_{2}} & - e^{i q_{3} x_{2}} & - e^{- i q_{3} x_{2}} & 0 & 0 & 0 & 0 & 0 \\ 0 & q_{2} e^{i q_{2} x_{2}} & - q_{2} e^{- i q_{2} x_{2}} & - q_{3} e^{i q_{3} x_{2}} & q_{3} e^{- i q_{3} x_{2}} & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & e^{i q_{3} x_{3}} & e^{- i q_{3} x_{3}} & - e^{i q_{4} x_{3}} & - e^{- i q_{4} x_{3}} & 0 & 0 & 0 \\ 0 & 0 & 0 & q_{3} e^{i q_{3} x_{3}} & - q_{3} e^{- i q_{3} x_{3}} & - q_{4} e^{i q_{4} x_{3}} & q_{4} e^{- i q_{4} x_{3}} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & e^{i q_{4} x_{4}} & e^{- i q_{4} x_{4}} & - e^{i q_{5} x_{4}} & - e^{- i q_{5} x_{4}} & 0 \\ 0 & 0 & 0 & 0 & 0 & q_{4} e^{i q_{4} x_{4}} & - q_{4} e^{- i q_{4} x_{4}} & - q_{5} e^{i q_{5} x_{4}} & q_{5} e^{- i q_{5} x_{4}} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & e^{i q_{5} x_{5}} & e^{- i q_{5} x_{5}} & - e^{i q_{6} x_{5}} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & q_{5} e^{i q_{5} x_{5}} & - q_{5} e^{- i q_{5} x_{5}} & - q_{6} e^{i q_{6} x_{5}} \end{matrix})$

% paridad: 1 (simétrica), -1 (antisimétrica)
function res =niveles_solido_1(x, V, E, paridad)  
    N=length(x)-1;
    q=zeros(N+1,1);
    for i=1:N+1
        q(i)=sqrt(E-V(i));
    end
    
    f=@(z,q) [exp(1i*q*z) exp(-1i*q*z); q*exp(1i*q*z) -q*exp(-1i*q*z)];
    
    M=zeros(2*N);
    M(1,1)=exp(1i*q(1)*x(1))+paridad*exp(-1i*q(1)*x(1));
    M(2,1)=q(1)*(exp(1i*q(1)*x(1))-paridad*exp(-1i*q(1)*x(1)));
    M(1:2,2:3)=-f(x(1),q(2));
    for i=2:N-1
        M(2*i-1:2*i, 2*i-2:2*i-1)=f(x(i),q(i));
        M(2*i-1:2*i, 2*i:2*i+1)=-f(x(i),q(i+1));
    end
    M(2*N-1:2*N,2*N-2:2*N-1)=f(x(N),q(N));
    M(2*N-1,2*N)=-exp(1i*q(N+1)*x(N));
    M(2*N,2*N)=-q(N+1)*exp(1i*q(N+1)*x(N));
    resultado=det(M);
    res=real(resultado)+imag(resultado);
end

Obtenemos los coeficientes A_j y B_j a partir de A_j+1 y B_j+1, multiplicando matrices de 2x2

$\begin{array}{l} (\begin{matrix} e^{i q_{j} x_{j}} & e^{- i q_{j} x_{j}} \\ q_{j} e^{i q_{j} x_{j}} & - q_{j} e^{- i q_{j} x_{j}} \end{matrix}) (\begin{matrix} A_{j} \\ B_{j} \end{matrix}) = (\begin{matrix} e^{i q_{j + 1} x_{j}} & e^{- i q_{j + 1} x_{j}} \\ q_{j + 1} e^{i q_{j + 1} x_{j}} & - q_{j + 1} e^{- i q_{j + 1} x_{j}} \end{matrix}) (\begin{matrix} A_{j + 1} \\ B_{j + 1} \end{matrix}) \\ (\begin{matrix} A_{j} \\ B_{j} \end{matrix}) = {(\begin{matrix} e^{i q_{j} x_{j}} & e^{- i q_{j} x_{j}} \\ q_{j} e^{i q_{j} x_{j}} & - q_{j} e^{- i q_{j} x_{j}} \end{matrix})}^{- 1} (\begin{matrix} e^{i q_{j + 1} x_{j}} & e^{- i q_{j + 1} x_{j}} \\ q_{j + 1} e^{i q_{j + 1} x_{j}} & - q_{j + 1} e^{- i q_{j + 1} x_{j}} \end{matrix}) (\begin{matrix} A_{j + 1} \\ B_{j + 1} \end{matrix}) \\ (\begin{matrix} A_{j} \\ B_{j} \end{matrix}) = (\begin{matrix} e^{- i q_{j} x_{j}} / 2 & e^{- i q_{j} x_{j}} / 2 q_{j} \\ e^{i q_{j} x_{j}} / 2 & - e^{- i q_{j} x_{j}} / 2 q_{j} \end{matrix}) (\begin{matrix} e^{i q_{j + 1} x_{j}} & e^{- i q_{j + 1} x_{j}} \\ q_{j + 1} e^{i q_{j + 1} x_{j}} & - q_{j + 1} e^{- i q_{j + 1} x_{j}} \end{matrix}) (\begin{matrix} A_{j + 1} \\ B_{j + 1} \end{matrix}) \end{array}$

Comprobamos la expresión de la matriz inversa con MATLAB

>> syms q x;
>> M=[exp(1i*q*x) exp(-1i*q*x);q*exp(1i*q*x) -q*exp(-1i*q*x)];
>> M1=inv(M)
M1 = 
[ exp(-q*x*i)/2, exp(-q*x*i)/(2*q)]
[  exp(q*x*i)/2, -exp(q*x*i)/(2*q)]
>> M*M1
ans =
[ 1, 0]
[ 0, 1]

Sabiendo que A_N+1=1 y B_N+1=0, calculamos A₁ y B₁

Para las funciones de onda simétricas, A₁ - B₁=0, y para las antisimétricas A₁ + B₁=0

function res =niveles_solido(x, V, E, paridad)  
    N=length(x)-1;
    q=zeros(N+1,1);
    for i=1:N+1
        q(i)=sqrt(E-V(i));
    end

    f=@(z,q) [exp(1i*q*z) exp(-1i*q*z); q*exp(1i*q*z) -q*exp(-1i*q*z)]; 
    g=@(z,q) [exp(-1i*q*z) exp(-1i*q*z)/q; exp(1i*q*z) -exp(1i*q*z)/q]/2; 

    A=[1;0];
    for i=N:-1:1
        A=g(x(i),q(i))*f(x(i),q(i+1))*A;
    end
   res=real(A(1)-paridad*A(2))+imag(A(1)-paridad*A(2));
end

Para buscar los intervalos en los que la función niveles_solido o niveles_solido_1 cambia de signo utilizamos la función buscar_intervalos

function xb = buscar_intervalos(f,a,b,n)
    x = a:(b-a)/n:b;
    j = 0; 
    y1=f(x(1));
    xb=[];
    for i = 1:length(x)-1
        y2=f(x(i+1));
        if sign(y1) ~= sign(y2) 
            j = j + 1;
            xb(j,1) = x(i);
            xb(j,2) = x(i+1);
        end
        y1=y2;
    end
    if isempty(xb) 
        disp('no se han encontrado cambios de signo')
    else
        disp(['número de intervalos:' int2str(j)]) 
    end
end

Completamos el script para calcular y representar los niveles de energía de un sistema de N pozos de potencial

...
paridad=-1; %antisimétrico
f=@(E) niveles_solido(x, V, E, paridad);
xb=buscar_intervalos(f,0.1,H-0.1,100);
nb=size(xb);
for i=1:nb(1)
    impar(i)=fzero(f,[xb(i,1) xb(i,2)]);
end

paridad=1; %simétrico
f=@(E) niveles_solido(x, V, E, paridad);
xb=buscar_intervalos(f,0.1,H-0.1,100);
nb=size(xb);
for i=1:nb(1)
    par(i)=fzero(f,[xb(i,1) xb(i,2)]);
end
disp(par);   %niveles de energía, estados simétricos
disp(impar); %niveles de energía, estados antisimétricos

%niveles
for i=1:length(par)
    line([-x(N+1) x(N+1)],[par(i) par(i)], 'color','r')
end
for i=1:length(impar)
    line([-x(N+1) x(N+1)],[impar(i) impar(i)], 'color','b')
end

hold off
ylim([0,H+1])
xlim([-x(N+1) x(N+1)])
xlabel('x');
ylabel('V')
title('Sistema de pozos de potencial')

%color rojo (simétricos)
1.0064    1.1390    1.2971    3.8604    4.5667
%color azul (antisimétricos)
1.0600    1.2264    3.6568    4.1754

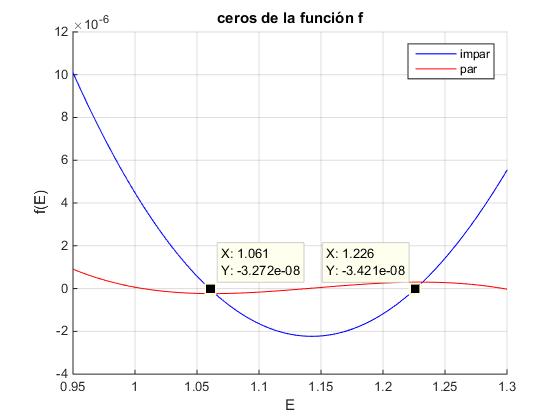
Ejemplo de los ceros de la función f(E) o niveles_solido para N=6, a=2, b=1. En color rojo para el valor de la varaible paridad=1 y en color azul para paridad=-1

Funciones de onda

En esta sección representamos la función de onda de un nivel dado de energía

Volvemos al cálculo de los niveles de energía, a las relaciones de continuidad de la función de onda en entre los coeficientes A_j y B_j con los coeficientes A_j+1 y B_j+1, sabiendo que A_N+1=1 y B_N+1=0

$\begin{array}{l} (\begin{matrix} A_{j} \\ B_{j} \end{matrix}) = (\begin{matrix} e^{- i q_{j} x_{j}} / 2 & e^{- i q_{j} x_{j}} / 2 q_{j} \\ e^{i q_{j} x_{j}} / 2 & - e^{- i q_{j} x_{j}} / 2 q_{j} \end{matrix}) (\begin{matrix} e^{i q_{j + 1} x_{j}} & e^{- i q_{j + 1} x_{j}} \\ q_{j + 1} e^{i q_{j + 1} x_{j}} & - q_{j + 1} e^{- i q_{j + 1} x_{j}} \end{matrix}) (\begin{matrix} A_{j + 1} \\ B_{j + 1} \end{matrix}) \\ A_{N + 1} = 1, B_{N + 1} = 0 \end{array}$

La función de onda en el intervalo x_j-1 y x_j es

$Ψ_{j} (x) = A_{j} \exp (i q_{j} x) + B_{j} \exp (- i q_{j} x) q_{j} = \sqrt{E - V_{j}}$

Si coincide con una barrera q_j es imaginario y si coincide con una pozo q_j es real.

$\begin{array}{l} Ψ_{j} (x) = A_{j} \exp (- k x) + B_{j} \exp (k x) k = \sqrt{V_{j} - E} \\ Ψ_{j} (x) = A_{j} \exp (i q x) + B_{j} \exp (- i q x) q = \sqrt{E - V_{j}} \end{array}$

Antes de representar la función de onda es necesario normalizarla, hacer que

$\int_{- \infty}^{\infty} {| Ψ (x) |}^{2} d x = 1 \int_{0}^{x_{1}} {| Ψ_{1} (x) |}^{2} d x + \sum_{j = 2}^{N} \int_{x_{j - 1}}^{x_{j}} {| Ψ_{j} (x) |}^{2} d x + \int_{x_{N}}^{\infty} {| Ψ_{N + 1} (x) |}^{2} d x = \frac{1}{2}$

El último término es el más sencillo de calcular

$\begin{array}{l} Ψ_{N + 1} (x) = A_{N + 1} \exp (- k x) q_{N + 1} = i k = \sqrt{E - V_{N + 1}} \\ \int_{x_{N}}^{\infty} {| Ψ_{N + 1} (x) |}^{2} d x = \frac{A_{N + 1} A_{N + 1}^{*}}{2 k} \exp (- 2 k x_{N}) = - \frac{A_{N + 1} A_{N + 1}^{*}}{2 i q_{N + 1}} \exp (2 i q_{N + 1} x_{N}) \end{array}$

Supongamos que j coincide con una barrera

$\begin{array}{l} Ψ_{j} (x) = A_{j} \exp (- k x) + B_{j} \exp (k x) q_{j} = \sqrt{E - V_{j}} = i k \\ \int_{x_{j - 1}}^{x_{j}} {| Ψ_{j} (x) |}^{2} d x = \int_{x_{j - 1}}^{x_{j}} (A_{j} B_{j}^{*} + B_{j} A_{j}^{*} + A_{j} A_{j}^{*} \exp (- 2 k x) + B_{j} B_{j}^{*} \exp (2 k x)) d x = \\ (A_{j} B_{j}^{*} + B_{j} A_{j}^{*}) (x_{j} - x_{j - 1}) - \frac{A_{j} A_{j}^{*}}{2 k} (e^{- 2 k x_{j}} - e^{- 2 k x_{j - 1}}) + \frac{B_{j} B_{j}^{*}}{2 k} (e^{2 k x_{j}} - e^{2 k x_{j - 1}}) = \\ (A_{j} B_{j}^{*} + B_{j} A_{j}^{*}) (x_{j} - x_{j - 1}) + \frac{A_{j} A_{j}^{*}}{2 i q_{j}} (e^{2 i q_{j} x_{j}} - e^{2 i q_{j} x_{j - 1}}) - \frac{B_{j} B_{j}^{*}}{2 i q_{j}} (e^{- 2 i q_{j} x_{j}} - e^{- 2 i q_{j} x_{j - 1}}) \end{array}$

Supongamos que j coincide con un pozo

$\begin{array}{l} Ψ_{j} (x) = A_{j} \exp (i q x) + B_{j} \exp (- i q x) q_{j} = \sqrt{E - V_{j}} = q \\ \int_{x_{j - 1}}^{x_{j}} {| Ψ_{j} (x) |}^{2} d x = \int_{x_{j - 1}}^{x_{j}} (A_{j} A_{j}^{*} + B_{j} B_{j}^{*} + A_{j} B_{j}^{*} \exp (2 i q x) + B_{j} A_{j}^{*} \exp (- 2 i q x)) d x = \\ (A_{j} A_{j}^{*} + B_{j} B_{j}^{*}) (x_{j} - x_{j - 1}) + \frac{A_{j} B_{j}^{*}}{2 i q} (e^{2 i q x_{j}} - e^{2 i q x_{j - 1}}) - \frac{B_{j} A_{j}^{*}}{2 i q} (e^{- 2 i q x_{j}} - e^{- 2 i q x_{j - 1}}) = \\ (A_{j} A_{j}^{*} + B_{j} B_{j}^{*}) (x_{j} - x_{j - 1}) + \frac{A_{j} B_{j}^{*}}{2 i q_{j}} (e^{2 i q_{j} x_{j}} - e^{2 i q_{j} x_{j - 1}}) - \frac{B_{j} A_{j}^{*}}{2 i q_{j}} (e^{- 2 i q_{j} x_{j}} - e^{- 2 i q_{j} x_{j - 1}}) \end{array}$

....
%niveles de energía
disp(par)
disp(impar)
%funciones de onda, para un nivel de energía
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
e_n=impar(1);
paridad=-1;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 q=zeros(N+1,1);
 for i=1:N+1
    q(i)=sqrt(e_n-V(i));
 end

f=@(z,q) [exp(1i*q*z) exp(-1i*q*z); q*exp(1i*q*z) -q*exp(-1i*q*z)]; 
g=@(z,q) [exp(-1i*q*z) exp(-1i*q*z)/q; exp(1i*q*z) -exp(1i*q*z)/q]/2; 

A=[1;0];
%q imaginario E<V, barrera
suma=-exp(2*1i*q(N+1)*x(N))/(2*1i*q(N+1));
for i=N:-2:2
    A=g(x(i),q(i))*f(x(i),q(i+1))*A; 
    %q real E>V, pozo
    suma=suma+(A(1)*conj(A(1))+A(2)*conj(A(2)))*(x(i)-x(i-1))
+A(1)*conj(A(2))*(exp(2*1i*q(i)*x(i))-exp(2*1i*q(i)*x(i-1)))/(2*1i*q(i))
-A(2)*conj(A(1))*(exp(-2*1i*q(i)*x(i))-exp(-2*1i*q(i)*x(i-1)))/(2*1i*q(i));
    A=g(x(i-1),q(i-1))*f(x(i-1),q(i))*A; 
    %q imaginario E<V, barrera
    if i==2
        break;
    else
        suma=suma+(A(1)*conj(A(2))+A(2)*conj(A(1)))*(x(i-1)-x(i-2))
+A(1)*conj(A(1))*(exp(2*1i*q(i-1)*x(i-1))-exp(2*1i*q(i-1)*x(i-2)))
/(2*1i*q(i-1))
-A(2)*conj(A(2))*(exp(-2*1i*q(i-1)*x(i-1))-exp(-2*1i*q(i-1)*x(i-2)))
/(2*1i*q(i-1));
    end
end
%q real E>V
if rem(N,2)==1
    A=g(x(1),q(1))*f(x(1),q(2))*A; %pozo
    suma=suma+(A(1)*conj(A(1))+A(2)*conj(A(2)))*x(1)
+A(1)*conj(A(2))*(exp(2*1i*q(1)*x(1))-1)/(2*1i*q(1))
-A(2)*conj(A(1))*(exp(-2*1i*q(1)*x(1))-1)/(2*1i*q(1));
else %barrera
    suma=suma+(A(1)*conj(A(2))+A(2)*conj(A(1)))*x(1)
+(A(1)*conj(A(1))*(exp(2*1i*q(1)*x(1))-1)
-A(2)*conj(A(2))*(exp(-2*1i*q(1)*x(1))-1))/(2*1i*q(1));  
end

A=[1;0];
z=linspace(x(N),x(N+1),20);
phi=exp(1i*q(N+1)*z)/sqrt(suma);
y=real(phi)+imag(phi);
plot(z,e_n+y,'r')
plot(-z,e_n+paridad*y,'r')

for i=N:-2:2
    A=g(x(i),q(i))*f(x(i),q(i+1))*A;
    z=linspace(x(i-1),x(i),20);
    phi=(A(1)*exp(1i*q(i)*z)+A(2)*exp(-1i*q(i)*z))/sqrt(suma);
    y=real(phi)+imag(phi);
    plot(z,e_n+y,'r')
    plot(-z,e_n+paridad*y,'r')
    A=g(x(i-1),q(i-1))*f(x(i-1),q(i))*A;
    if i==2
        break;
    else
        z=linspace(x(i-2),x(i-1),20);
        phi=(A(1)*exp(1i*q(i-1)*z)+A(2)*exp(-1i*q(i-1)*z))/sqrt(suma);
        y=real(phi)+imag(phi);
        plot(z,e_n+y,'r')
        plot(-z,e_n+paridad*y,'r')
    end
end
if rem(N,2)==0
    z=linspace(0,x(1),20);
    phi=(A(1)*exp(1i*q(1)*z)+A(2)*exp(-1i*q(1)*z))/sqrt(suma);
    y=real(phi)+imag(phi);
    plot(z,e_n+y,'r')
    plot(-z,e_n+paridad*y,'r')
else
    A=g(x(1),q(1))*f(x(1),q(2))*A;
    z=linspace(0,x(1),20);
    phi=(A(1)*exp(1i*q(1)*z)+A(2)*exp(-1i*q(1)*z))/sqrt(suma);
    y=real(phi)+imag(phi);
    plot(z,e_n+y,'r')
    plot(-z,e_n+paridad*y,'r')
end
line([-x(N+1) x(N+1)],[e_n, e_n], 'color','b')  %nivel de energía
text(x(N+1), e_n,num2str(e_n),
'VerticalAlignment','bottom', 'HorizontalAlignment','right');


hold off
ylim([0,H+1])
xlim([-x(N+1) x(N+1)])
xlabel('x');
ylabel('V')
title('Sistema de pozos de potencial')

    1.0064    1.1390    1.2971    3.8604    4.5667  %par
    1.0600    1.2264    3.6568    4.1754      %impar

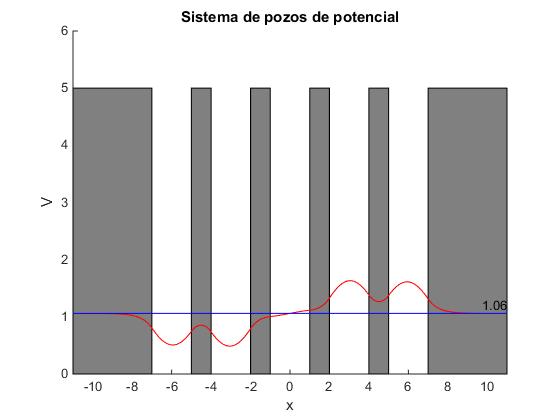
Para un sistema formado por N=5 pozos de potencial de anchura a=2 y separación b=1, en la ventana de comandos aprecen cinco niveles de energía correspondientes a estados simétricos y cuatro correspondientes a estados antisimétricos

Para visualizar una función de onda simétrica (par), escribimos en el lugar señalado del código MATLAB

e_n=par(1);
paridad=1;

Si queremos visualizar una función de onda antisimétrica (impar) escribimos

e_n=impar(2);
paridad=-1;

Atomo, molécula...sólido lineal

El átomo.

Sea el Número de pozos, N=1. Vamos a considerar el pozo de potencial como un modelo simplificado de átomo, contaremos el número de niveles de energía, observaremos su distribución y la representación de las funciones de onda correspondientes a cada uno de dichos niveles.

La molécula diatómica

Si el pozo de potencial simple nos da la imagen de un átomo, el pozo de potencial doble es una simplificación de la molécula diatómica.

Sea el Número de pozos, N=2. Observaremos que por cada nivel de energía del pozo de potencial simple, se producen dos niveles de energía próximos en el pozo de potencial doble. El nivel más bajo de cada doblete tiene una energía inferior a la correspondiente del pozo de potencial simple y además, es un estado simétrico. El desdoblamiento se incrementa a medida que disminuye la separación entre los pozos.

Los resultados anteriores permiten explicar las facetas esenciales de la unión covalente entre átomos iguales, en el mismo estado, para una distancia de equilibrio entre ambos.

El estado fundamental tiene una energía inferior a la de los dos átomos aislados, lo que configura una unión estable, la función de onda es simétrica.

El segundo nivel, tiene una energía superior a la de los átomos aislados, es una unión inestable, la función de onda es antisimétrica.

Sólido lineal

Un sistema de 3, 4, 5, etc. pozos de potencial representa un modelo simple de los enlaces π de las moléculas conjugadas lineales, tales como los polienos. Los electrones se mueven en una región descrita por un potencial periódico y cada nivel de energía atómico se divide en un número de niveles igual al número de átomos.

En general, en una red de N átomos cada nivel de energía atómico da lugar a N niveles cercanos. Cuando N es grande los niveles de energía están espaciados tan finamente que se puede decir que forman una banda continua de energía. (Véase la figura más abajo)

De acuerdo al Principio de Exclusión de Pauli, cada nivel puede acomodar dos electrones, uno con espín hacia arriba y otro con espín hacia abajo. Una banda de energía correspondiente a un estado atómico dado, puede acomodar un máximo de 2N electrones. Si la banda correspondiente a la capa atómica más externa, la ocupada por los electrones de valencia, no está completamente llena, se denomina banda de conducción, pero si lo está, se denomina banda de valencia y la banda vacía que queda por encima recibe el nombre de banda de conducción. Dependiendo de la estructura de las bandas, los materiales tienen distintas propiedades eléctricas clasificándose en conductores, aisladores y semiconductores.

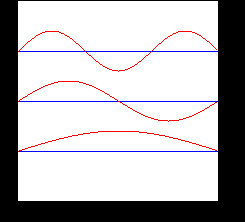
La representación gráfica de las funciones de onda de los primeros niveles de energía de un sistema de muchos pozos de potencial, nos sugiere que se trata de funciones cuya forma es semejante a los modos de vibración de una cuerda, pero modulados por la función de onda de un pozo de potencial.

En la figura, se esquematiza los tres primeros modos de una cuerda vibrante.

Niveles de energía

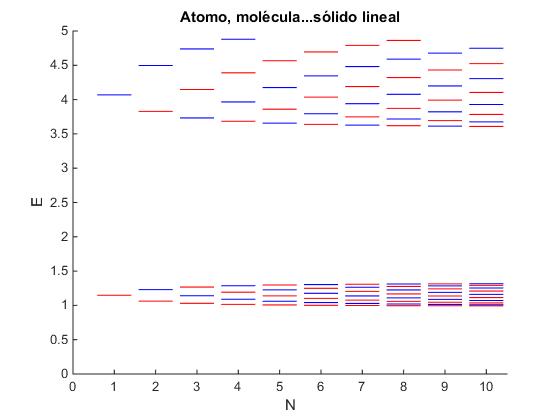
Representamos en la misma ventana gráfica, los niveles de energía para N=1, 2,...10 pozos de potencial

Podremos observar de un vistazo la constitución efectiva de las bandas de energía por adición sucesiva de "átomos" a la cadena lineal. En particular, como se multiplican los niveles de energía al incrementar el número de pozos de potencial y cómo se van agrupando los niveles en determinados intervalos de energía, que darán lugar niveles continuos de energía denominadas bandas, cuando el número de pozos sea muy grande, tal como veremos en el modelo de sólido lineal

a=2;  %anchura del pozo
b=1; %separación entre pozos
H=5.0; %altura del pozo

hold on

for N=1:10; %número de pozos
%potencial periódico
    x=zeros(N+1,1);
    V=zeros(N+1,1);
    if rem(N,2)==0
        V(1)=H;
        x(1)=b/2;
        for i=2:2:N-1
            x(i)=x(i-1)+a;
            V(i)=0;
            x(i+1)=x(i)+b;
            V(i+1)=H;
        end
        x(N)=x(N-1)+a;
    else
        x(1)=a/2;
        V(1)=0;
        for i=2:2:N
            x(i)=x(i-1)+b;
            V(i)=H;
            x(i+1)=x(i)+a;
            V(i+1)=0;
        end
    end
    x(N+1)=x(N)+2*a;
    V(N+1)=H;
%calcula los niveles de energía

    paridad=-1;
    f=@(E) niveles_solido(x, V, E, paridad);
    xb=buscar_intervalos(f,0.1,H-0.1,100);
    nb=size(xb);
    for i=1:nb(1)
        impar(i)=fzero(f,[xb(i,1) xb(i,2)]);
    end

    paridad=1;
    f=@(E) niveles_solido(x, V, E, paridad);
    xb=buscar_intervalos(f,0.1,H-0.1,100);
    nb=size(xb);
    for i=1:nb(1)
        par(i)=fzero(f,[xb(i,1) xb(i,2)]);
    end
 
%niveles
    for i=1:length(par)
        line([N-0.4 N+0.4],[par(i) par(i)], 'color','r')
    end
    for i=1:length(impar)
        line([N-0.4 N+0.4],[impar(i) impar(i)], 'color','b')
    end
end
hold off
ylim([0 H])
xlim([0 10.5])
xlabel('N');
ylabel('E')
title('Atomo, molécula...sólido lineal')