Sistema de potenciales delta de Dirac

Analizaremos un modelo sencillo, formado por tres potenciales delta de Dirac igualmente espaciados y situados en el interior de un pozo de potencial de altura infinita y anchura 4a, siendo a la distancia entre dos potenciales consecutivos, tal como se muestra en la figura

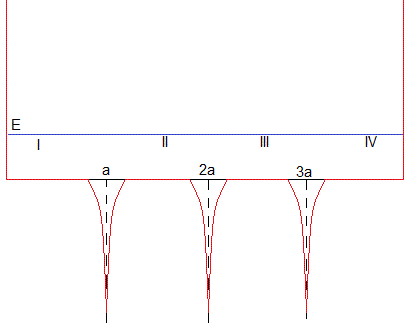
Resolveremos la ecuación de Schrödinger, primero para energías positivas E>0, y a continuación, para energías negativas E<0

$- \frac{ℏ^{2}}{2 m} \frac{d^{2} ψ (x)}{d x^{2}} + V (x) \cdot ψ (x) = E \cdot ψ (x)$

El potencial V(x) es

${\begin{cases} V (0) = \infty \\ 0 < x < a - ε, V (x) = 0 \\ a - ε < x < a + ε, V (x) = - α \frac{ℏ^{2}}{2 m} δ (x - a) \\ a + ε < x < 2 a - ε, V (x) = 0 \\ 2 a - ε < x < 2 a + ε, V (x) = - α \frac{ℏ^{2}}{2 m} δ (x - 2 a) \\ 2 a + ε < x < 3 a - ε, V (x) = 0 \\ 3 a - ε < x < 3 a + ε, V (x) = - α \frac{ℏ^{2}}{2 m} δ (x - 3 a) \\ 3 a + ε < x < 4 a, V (x) = 0 \\ V (4 a) = \infty \end{cases}$

Siendo ε→0, una cantidad que tiende a cero

Primera solución

Energías E>0

Las soluciones de la ecuación de Schrödinger en las regiones I, I, III y IV con potencial V(x)=0 son

$\begin{array}{l} \frac{d^{2} ψ}{d x^{2}} + \frac{2 m}{ℏ^{2}} E \cdot ψ = 0, E > 0 \\ \frac{d^{2} ψ}{d x^{2}} + k^{2} \cdot ψ = 0, k^{2} = \frac{2 m}{ℏ^{2}} E \\ ψ_{I} (x) = A_{1} \exp (- i k x) + B_{1} \exp (i k x) \\ ψ_{I I} (x) = A_{2} \exp (- i k x) + B_{2} \exp (i k x) \\ ψ_{I I I} (x) = A_{3} \exp (- i k x) + B_{3} \exp (i k x) \\ ψ_{I V} (x) = A_{4} \exp (- i k x) + B_{4} \exp (i k x) \end{array}$

Condiciones en los extremos x=0, y x=4a donde V(x)=∞

$\begin{array}{l} ψ_{I} (0) = A_{1} + B_{1} = 0 \\ ψ_{I V} (4 a) = A_{4} \exp (- i k \cdot 4 a) + B_{4} \exp (i k \cdot 4 a) = 0 \end{array}$

En en x=a, x=2a y x=3a la función de onda es continua

$\begin{array}{l} ψ_{I} (a) = ψ_{I I} (a) \\ ψ_{I I} (2 a) = ψ_{I I I} (2 a) \\ ψ_{I I I} (3 a) = ψ_{I V} (3 a) \\ {\begin{cases} A_{1} \exp (- i k a) + B_{1} \exp (i k a) = A_{2} \exp (- i k a) + B_{2} \exp (i k a) \\ A_{2} \exp (- i k \cdot 2 a) + B_{2} \exp (i k \cdot 2 a) = A_{3} \exp (- i k \cdot 2 a) + B_{3} \exp (i k \cdot 2 a) \\ A_{3} \exp (- i k \cdot 3 a) + B_{3} \exp (i k \cdot 3 a) = A_{4} \exp (- i k \cdot 3 a) + B_{4} \exp (i k \cdot 3 a) \end{cases} \end{array}$

La derivada primera de la función de onda NO es continua en x=a, x=2a y x=3a

Integramos la ecuación de Schrödinger en el pequeño intervalo de a-ε a a+ε

$\begin{array}{l} - \frac{ℏ^{2}}{2 m} \int_{a - ε}^{a + ε} \frac{d^{2} ψ (x)}{d x^{2}} d x - \int_{a - ε}^{a + ε} α \frac{ℏ^{2}}{2 m} δ (x - a) \cdot ψ (x) \cdot d x = E \cdot \int_{a - ε}^{a + ε} ψ (x) \cdot d x \\ - \frac{ℏ^{2}}{2 m} \lim_{ε \to 0} ({\frac{d ψ_{I I} (x)}{d x} |}_{a + ε} - {\frac{d ψ_{I} (x)}{d x} |}_{a - ε}) - α \frac{ℏ^{2}}{2 m} ψ_{I} (a) = 0 \\ \lim_{ε \to 0} ({- i k A_{2} \exp (- i k x) + i k B_{2} \exp (i k x) |}_{a + ε} {- (- i k A_{1} \exp (- i k x) + i k B_{1} \exp (i k x)) |}_{a - ε}) + α (A_{1} \exp (- i k a) + B_{1} \exp (i k a)) = 0 \\ \lim_{ε \to 0} ((- i k A_{2} \exp (- i k (a + ε)) + i k B_{2} \exp (i k (a + ε))) - (- i k A_{1} \exp (- i k (a - ε)) + i k B_{1} \exp (i k (a - ε)))) + α (A_{1} \exp (- i k a) + B_{1} \exp (i k a)) = 0 \\ (- i k A_{2} \exp (- i k a) + i k B_{2} \exp (i k a)) - (- i k A_{1} \exp (- i k a) + i k B_{1} \exp (i k a))) + α (A_{1} \exp (- i k a) + B_{1} \exp (i k a)) = 0 \end{array}$

De modo similar, establecemos las otras dos ecuaciones que relacionan los coeficientes en x=2a y en x=3a

${\begin{cases} (\frac{α}{i k} + 1) A_{1} \exp (- i k a) + (\frac{α}{i k} - 1) B_{1} \exp (i k a) = A_{2} \exp (- i k a) - B_{2} \exp (i k a) \\ (\frac{α}{i k} + 1) A_{2} \exp (- i k \cdot 2 a) + (\frac{α}{i k} - 1) B_{2} \exp (i k \cdot 2 a) = A_{3} \exp (- i k \cdot 2 a) - B_{3} \exp (i k \cdot 2 a) \\ (\frac{α}{i k} + 1) A_{3} \exp (- i k \cdot 3 a) + (\frac{α}{i k} - 1) B_{3} \exp (i k \cdot 3 a) = A_{4} \exp (- i k \cdot 3 a) - B_{4} \exp (i k \cdot 3 a) \end{cases}$

En forma matricial la relación entre los coeficientes se escribe

$\begin{array}{l} (\begin{matrix} e^{- i k a} & e^{i k a} \\ (\frac{α}{i k} + 1) e^{- i k a} & (\frac{α}{i k} - 1) e^{i k a} \end{matrix}) (\begin{matrix} A_{1} \\ B_{1} \end{matrix}) = (\begin{matrix} e^{- i k a} & e^{i k a} \\ e^{- i k a} & - e^{i k a} \end{matrix}) (\begin{matrix} A_{2} \\ B_{2} \end{matrix}) \\ (\begin{matrix} e^{- i k \cdot 2 a} & e^{i k \cdot 2 a} \\ (\frac{α}{i k} + 1) e^{- i k \cdot 2 a} & (\frac{α}{i k} - 1) e^{i k \cdot 2 a} \end{matrix}) (\begin{matrix} A_{2} \\ B_{2} \end{matrix}) = (\begin{matrix} e^{- i k \cdot 2 a} & e^{i k \cdot 2 a} \\ e^{- i k \cdot 2 a} & - e^{i k \cdot 2 a} \end{matrix}) (\begin{matrix} A_{3} \\ B_{3} \end{matrix}) \\ (\begin{matrix} e^{- i k \cdot 3 a} & e^{i k \cdot 3 a} \\ (\frac{α}{i k} + 1) e^{- i k \cdot 3 a} & (\frac{α}{i k} - 1) e^{i k \cdot 3 a} \end{matrix}) (\begin{matrix} A_{3} \\ B_{3} \end{matrix}) = (\begin{matrix} e^{- i k \cdot 3 a} & e^{i k \cdot 3 a} \\ e^{- i k \cdot 3 a} & - e^{i k \cdot 3 a} \end{matrix}) (\begin{matrix} A_{4} \\ B_{4} \end{matrix}) \end{array}$

Niveles de energía

Relacionamos A₁ y B₁ con A₄ y B₄

$\begin{array}{l} (\begin{matrix} A_{1} \\ B_{1} \end{matrix}) = {(\begin{matrix} e^{- i k a} & e^{i k a} \\ (\frac{α}{i k} + 1) e^{- i k a} & (\frac{α}{i k} - 1) e^{i k a} \end{matrix})}^{- 1} (\begin{matrix} e^{- i k a} & e^{i k a} \\ e^{- i k a} & - e^{i k a} \end{matrix}) (\begin{matrix} A_{2} \\ B_{2} \end{matrix}) \\ (\begin{matrix} A_{2} \\ B_{2} \end{matrix}) = {(\begin{matrix} e^{- i k \cdot 2 a} & e^{i k \cdot 2 a} \\ (\frac{α}{i k} + 1) e^{- i k \cdot 2 a} & (\frac{α}{i k} - 1) e^{i k \cdot 2 a} \end{matrix})}^{- 1} (\begin{matrix} e^{- i k \cdot 2 a} & e^{i k \cdot 2 a} \\ e^{- i k \cdot 2 a} & - e^{i k \cdot 2 a} \end{matrix}) (\begin{matrix} A_{3} \\ B_{3} \end{matrix}) \\ (\begin{matrix} A_{3} \\ B_{3} \end{matrix}) = {(\begin{matrix} e^{- i k \cdot 3 a} & e^{i k \cdot 3 a} \\ (\frac{α}{i k} + 1) e^{- i k \cdot 3 a} & (\frac{α}{i k} - 1) e^{i k \cdot 3 a} \end{matrix})}^{- 1} (\begin{matrix} e^{- i k \cdot 3 a} & e^{i k \cdot 3 a} \\ e^{- i k \cdot 3 a} & - e^{i k \cdot 3 a} \end{matrix}) (\begin{matrix} A_{4} \\ B_{4} \end{matrix}) \end{array}$

El resultado de la relación entre A₁, B₁ y A₄ y B₄ es el producto de seis matrices

$\begin{array}{l} (\begin{matrix} A_{1} \\ B_{1} \end{matrix}) = (M_{a}^{- 1} N_{a}) (M_{2 a}^{- 1} N_{2 a}) (M_{3 a}^{- 1} N_{3 a}) (\begin{matrix} A_{4} \\ B_{4} \end{matrix}) \\ M_{n a}^{- 1} = {(\begin{matrix} e^{- i k n a} & e^{i k n a} \\ (\frac{α}{i k} + 1) e^{- i k n a} & (\frac{α}{i k} - 1) e^{i k n a} \end{matrix})}^{- 1}, n = 1,2,3 \\ N_{n a} = (\begin{matrix} e^{- i k n a} & e^{i k n a} \\ e^{- i k n a} & - e^{i k n a} \end{matrix}) \end{array}$

Teniendo en cuenta, la relaciones en los extremos x=0 y x=4a, obtenemos la ecuación transcendente

$\begin{array}{l} (\begin{matrix} A_{1} \\ - A_{1} \end{matrix}) = (\begin{matrix} t_{11} & t_{12} \\ t_{21} & t_{22} \end{matrix}) (\begin{matrix} A_{4} \\ - A_{4} e^{- 2 i k \cdot 4 a} \end{matrix}) \\ t_{11} + t_{21} - (t_{12} + t_{22}) e^{- 2 i k \cdot 4 a} = 0 \end{array}$

Recordamos que la matriz inversa de una matriz 2×2 es

${(\begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix})}^{- 1} = \frac{1}{| \begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix} |} (\begin{matrix} a_{22} & - a_{12} \\ - a_{21} & a_{11} \end{matrix})$

Sea un sistema formado por un pozo de potencial de altura infinita que contiene N=3 potenciales delta de Dirac separados a=1. El parámetro α=0.5 de dicho potencial delta

Representamos la parte real e imaginaria de la ecuación transcendente, dando valores a k entre 0.1 y 4

function delta_dirac_16
    a=1;
    alfa=0.5;
    N=3;
    ff=@(x) niveles_real(x);
    xb=buscar_intervalos(ff,0.1,4,50);
    nb=size(xb);
    kr=zeros(1,nb(1));
    for m=1:nb(1)
        temp=fzero(ff,[xb(m,1) xb(m,2)]);
        if abs(niveles_imag(temp))<0.1
            kr(m)=round(temp*1000)/1000;
        end
    end
    ff=@(x) niveles_imag(x);
    xb=buscar_intervalos(ff,0.1,4,50);
    nb=size(xb);
    ki=zeros(1,nb(1));
    for m=1:nb(1)
        temp=fzero(ff,[xb(m,1) xb(m,2)]);
        if abs(niveles_real(temp))<0.1
            ki(m)=round(temp*1000)/1000;
        end
    end
    j=1;
    kn=zeros(1,length(kr));
    for k=[ki,kr]
        if find(kn==k)
            continue;
        else
            kn(j)=k;
            j=j+1;
        end
    end
    for k=kn
        kn(kn==0)=[];
    end
    disp(kn)
    kk=linspace(0.1,4, 100);
    rp=zeros(1,length(kk));
    ri=zeros(1,length(kk));
    m=1;
    for k=kk
        rp(m)=niveles_real(k);
       ri(m)=niveles_imag(k);
        m=m+1;
    end
    hold on
    plot(kk,rp, kk,ri)
    for k=kn
        plot(k,0,'ko','markersize',4,'markerfacecolor','k')
    end
    hold off
    legend('real','imag','Location','best')
    grid on
    xlabel('k')
    ylabel('f(k)')
    title('Ecuación transcendente')

    function res=niveles_real(k)
        M=eye(2);
        fI=@(z) [(1+1i*alfa/k)*exp(1i*k*z), exp(1i*k*z); (1-1i*alfa/k)*
exp(-1i*k*z),-exp(-1i*k*z)]/2;  
        g=@(z) [exp(-1i*k*z), exp(1i*k*z); exp(-1i*k*z), -exp(1i*k*z)];
        for s=N:-1:1
             M=(fI(s*a)*g(s*a))*M;
        end
        resultado=M(2,1)+M(1,1)-exp(-2*1i*k*(N+1)*a)*(M(2,2)+M(1,2));
        res=real(resultado); 
    end
    function res=niveles_imag(k)
        M=eye(2);
        fI=@(z) [(1+1i*alfa/k)*exp(1i*k*z), exp(1i*k*z); (1-1i*alfa/k)*
exp(-1i*k*z),-exp(-1i*k*z)]/2;  
        g=@(z) [exp(-1i*k*z), exp(1i*k*z); exp(-1i*k*z), -exp(1i*k*z)];
        for s=N:-1:1
            M=(fI(s*a)*g(s*a))*M;
        end
        resultado=M(2,1)+M(1,1)-exp(-2*1i*k*(N+1)*a)*(M(2,2)+M(1,2));
        res=imag(resultado); 
    end

   function xb = buscar_intervalos(f,a,b,n)
       x = a:(b-a)/n:b;
        j = 0; 
        y1=f(x(1));
        xb=[];
        for i = 1:length(x)-1
            y2=f(x(i+1));
            if sign(y1) ~= sign(y2) 
                j = j + 1;
                xb(j,1) = x(i);
                xb(j,2) = x(i+1);
            end
            y1=y2;
        end
        if isempty(xb) 
            disp('no se han encontrado cambios de signo')
        else
            disp(['número de intervalos:' int2str(j)]) 
        end
    end
end

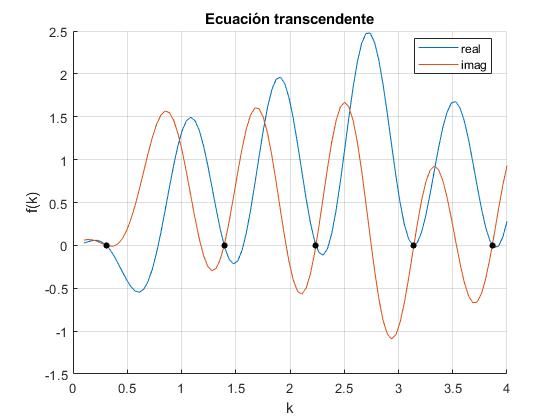
Los valores de k buscados (puntos de color negro) y por tanto, de los niveles de energía, son aquellos que hacen que la parte real e imaginaria sean nulas simultámeamente

Las raíces k comunes de la parte real e imaginaria de la ecuación transcendente se guardan en el vector kn. Los niveles de energía son proporcionales a k²

    0.3070    1.3930    2.2390    3.1420    3.8640

Funciones de onda

Dados los coeficientes A₁ y B₁=-A₁, obtenemos los coeficientes A₂ y B₂, A₃ y B₃, A₄ y B₄. En forma matricial

$\begin{array}{l} (\begin{matrix} A_{2} \\ B_{2} \end{matrix}) = {(\begin{matrix} e^{- i k a} & e^{i k a} \\ e^{- i k a} & - e^{i k a} \end{matrix})}^{- 1} (\begin{matrix} e^{- i k a} & e^{i k a} \\ (\frac{α}{i k} + 1) e^{- i k a} & (\frac{α}{i k} - 1) e^{i k a} \end{matrix}) (\begin{matrix} A_{1} \\ B_{1} \end{matrix}) \\ (\begin{matrix} A_{3} \\ B_{3} \end{matrix}) = {(\begin{matrix} e^{- i k \cdot 2 a} & e^{i k \cdot 2 a} \\ e^{- i k \cdot 2 a} & - e^{i k \cdot 2 a} \end{matrix})}^{- 1} (\begin{matrix} e^{- i k \cdot 2 a} & e^{i k \cdot 2 a} \\ (\frac{α}{i k} + 1) e^{- i k \cdot 2 a} & (\frac{α}{i k} - 1) e^{i k \cdot 2 a} \end{matrix}) (\begin{matrix} A_{2} \\ B_{2} \end{matrix}) \\ (\begin{matrix} A_{4} \\ B_{4} \end{matrix}) = {(\begin{matrix} e^{- i k \cdot 3 a} & e^{i k \cdot 3 a} \\ e^{- i k \cdot 3 a} & - e^{i k \cdot 3 a} \end{matrix})}^{- 1} (\begin{matrix} e^{- i k \cdot 3 a} & e^{i k \cdot 3 a} \\ (\frac{α}{i k} + 1) e^{- i k \cdot 3 a} & (\frac{α}{i k} - 1) e^{i k \cdot 3 a} \end{matrix}) (\begin{matrix} A_{3} \\ B_{3} \end{matrix}) \end{array}$

El coeficiente A₁ se determina de modo que la suma

$\begin{array}{l} \sum_{n = 1}^{N + 1} \int_{(n - 1) a}^{n a} (A_{n} e^{- i k x} + B_{n} e^{i k x}) (A_{n}^{*} e^{i k x} + B_{n}^{*} e^{- i k x}) d x = 1 \\ \sum_{n = 1}^{N + 1} (A_{n} A_{n}^{*} + B_{n} B_{n}^{*}) a - \frac{A_{n} B_{n}^{*}}{2 i k} (e^{- 2 i k (n + 1) a} - e^{- 2 i k \cdot n a}) + \frac{B_{n} A_{n}^{*}}{2 i k} (e^{2 i k (n + 1) a} - e^{2 i k \cdot n a}) = 1 \end{array}$

Añadimos al script anterior, el código que representa las funciones de onda correspondientes a los tres primeros niveles de energía

function delta_dirac_17
    a=1;
    alfa=0.5;
    N=3;
    ff=@(x) niveles_real(x);
    xb=buscar_intervalos(ff,0.1,4,50);
    nb=size(xb);
    kr=zeros(1,nb(1));
    for m=1:nb(1)
        temp=fzero(ff,[xb(m,1) xb(m,2)]);
        if abs(niveles_imag(temp))<0.1
            kr(m)=round(temp*1000)/1000;
        end
    end
    ff=@(x) niveles_imag(x);
    xb=buscar_intervalos(ff,0.1,4,50);
    nb=size(xb);
    ki=zeros(1,nb(1));
    for m=1:nb(1)
        temp=fzero(ff,[xb(m,1) xb(m,2)]);
        if abs(niveles_real(temp))<0.1
            ki(m)=round(temp*1000)/1000;
        end
    end
    j=1;
    kn=zeros(1,length(kr));
    for k=[ki,kr]
        if find(kn==k)
            continue;
        else
            kn(j)=k;
            j=j+1;
        end
    end
    for k=kn
        kn(kn==0)=[];
    end
    disp(kn)
%código que representa las funciones de onda %%%%%%%%%%%
    A=zeros(1,N+1);
    B=zeros(1,N+1);
    A(1)=1; B(1)=-1;
    for k=kn(1:3)
        f=@(z) [exp(-1i*k*z), exp(1i*k*z); (1-1i*alfa/k)*exp(-1i*k*z), 
-(1+1i*alfa/k)*exp(1i*k*z)]; 
        gI=@(z) [exp(1i*k*z), exp(1i*k*z); exp(-1i*k*z), -exp(-1i*k*z)]/2;
        suma=(A(1)^2+B(1)^2)*a+A(1)*B(1)*1i*(exp(-2*1i*k*a)-1)/(2*k)-
A(1)*B(1)*1i*(exp(2*1i*k*a)-1)/(2*k);
        for m=1:N
            Z=gI(m*a)*f(m*a)*[A(m);B(m)];
            A(m+1)=Z(1);
            B(m+1)=Z(2);
            suma=suma+(A(m+1)*A(m+1)'+B(m+1)*B(m+1)')*a+A(m+1)*B(m+1)'*
1i*(exp(-2*1i*k*(m+1)*a)-exp(-2*1i*k*m*a))/(2*k)-A(m+1)'*B(m+1)*1i*
(exp(2*1i*k*(m+1)*a)-exp(2*1i*k*m*a))/(2*k);
        end
        hold on
        for m=0:N
            fplot(@(x) imag(A(m+1)*exp(-1i*k*x)+B(m+1)*exp(1i*k*x))/sqrt(suma),
[m*a,(m+1)*a])
        end
    end
    hold off
    grid on
    xlabel('x')
    ylabel('\Phi(x)')
    title('Función de onda')
    
    function res=niveles_real(k)
        M=eye(2);
        fI=@(z) [(1+1i*alfa/k)*exp(1i*k*z), exp(1i*k*z); (1-1i*alfa/k)*
exp(-1i*k*z),-exp(-1i*k*z)]/2;  
        g=@(z) [exp(-1i*k*z), exp(1i*k*z); exp(-1i*k*z), -exp(1i*k*z)];
        for s=N:-1:1
             M=(fI(s*a)*g(s*a))*M;
        end
        resultado=M(2,1)+M(1,1)-exp(-2*1i*k*(N+1)*a)*(M(2,2)+M(1,2));
        res=real(resultado); 
    end
    function res=niveles_imag(k)
        M=eye(2);
        fI=@(z) [(1+1i*alfa/k)*exp(1i*k*z), exp(1i*k*z); (1-1i*alfa/k)*
exp(-1i*k*z),-exp(-1i*k*z)]/2;  
        g=@(z) [exp(-1i*k*z), exp(1i*k*z); exp(-1i*k*z), -exp(1i*k*z)];
        for s=N:-1:1
            M=(fI(s*a)*g(s*a))*M;
        end
        resultado=M(2,1)+M(1,1)-exp(-2*1i*k*(N+1)*a)*(M(2,2)+M(1,2));
        res=imag(resultado); 
    end

   function xb = buscar_intervalos(f,a,b,n)
       x = a:(b-a)/n:b;
        j = 0; 
        y1=f(x(1));
        xb=[];
        for i = 1:length(x)-1
            y2=f(x(i+1));
            if sign(y1) ~= sign(y2) 
                j = j + 1;
                xb(j,1) = x(i);
                xb(j,2) = x(i+1);
            end
            y1=y2;
        end
        if isempty(xb) 
            disp('no se han encontrado cambios de signo')
        else
            disp(['número de intervalos:' int2str(j)]) 
        end
    end
end

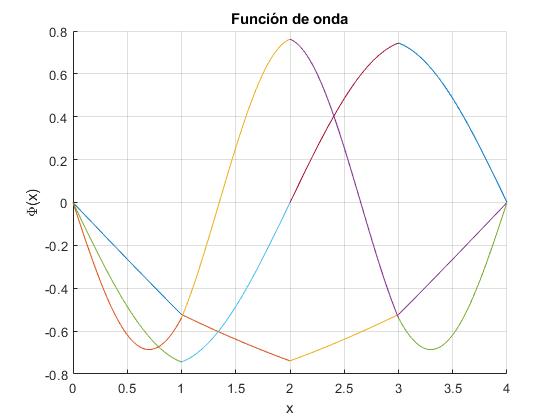
Cambiamos el parámetro α=2, y representamos las funciones de onda correspondientes a los dos primeros niveles de energía

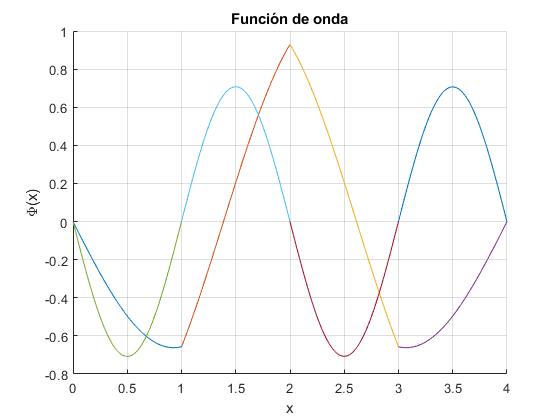
Primeros valores de k raíz de la ecuación transcendente (son nulas la parte real e imaginaria)

    1.6910    3.1420    3.6970

Pozo de potencial infinito

Cuando no hay potenciales delta, α=0, los niveles de energía para un pozo de potencial de altura infinita y de anchura 4a son proporcionales al cuadrado de

$k = \frac{n π}{(N + 1) a}$

>> (1:5)*pi/((N+1)*a)
ans =    0.7854    1.5708    2.3562    3.1416    3.9270

Las funciones de onda correspondientes a los tres primeros niveles de energía son

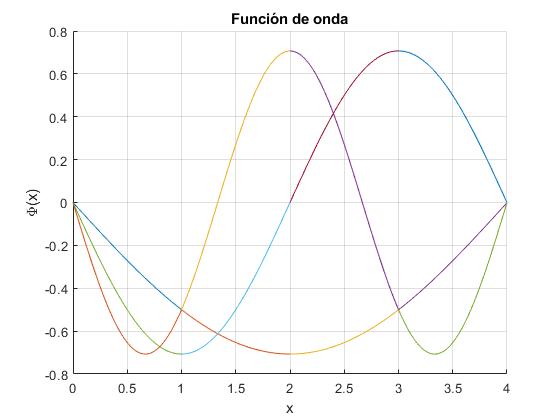
Compárese con el caso α=0.5

Energías E<0

Las soluciones de la ecuación de Schrödinger en las regiones I, I, III y IV con potencial V(x)=0 son

$\begin{array}{l} \frac{d^{2} ψ}{d x^{2}} + \frac{2 m}{ℏ^{2}} E \cdot ψ = 0, E < 0 \\ \frac{d^{2} ψ}{d x^{2}} - k^{2} \cdot ψ = 0, k^{2} = - \frac{2 m}{ℏ^{2}} E \\ ψ_{I} (x) = A_{1} \exp (- k x) + B_{1} \exp (k x) \\ ψ_{I I} (x) = A_{2} \exp (- k x) + B_{2} \exp (k x) \\ ψ_{I I I} (x) = A_{3} \exp (- k x) + B_{3} \exp (k x) \\ ψ_{I V} (x) = A_{4} \exp (- k x) + B_{4} \exp (k x) \end{array}$

Los cálculos son similares al apartado anterior E<0, sustituyendo ik por k. En forma matricial la relación de coeficientes es

$\begin{array}{l} (\begin{matrix} e^{- k a} & e^{k a} \\ (\frac{α}{k} + 1) e^{- k a} & (\frac{α}{k} - 1) e^{k a} \end{matrix}) (\begin{matrix} A_{1} \\ B_{1} \end{matrix}) = (\begin{matrix} e^{- k a} & e^{k a} \\ e^{- k a} & - e^{k a} \end{matrix}) (\begin{matrix} A_{2} \\ B_{2} \end{matrix}) \\ (\begin{matrix} e^{- i k \cdot 2 a} & e^{k \cdot 2 a} \\ (\frac{α}{k} + 1) e^{- k \cdot 2 a} & (\frac{α}{k} - 1) e^{k \cdot 2 a} \end{matrix}) (\begin{matrix} A_{2} \\ B_{2} \end{matrix}) = (\begin{matrix} e^{- k \cdot 2 a} & e^{k \cdot 2 a} \\ e^{- k \cdot 2 a} & - e^{k \cdot 2 a} \end{matrix}) (\begin{matrix} A_{3} \\ B_{3} \end{matrix}) \\ (\begin{matrix} e^{- k \cdot 3 a} & e^{k \cdot 3 a} \\ (\frac{α}{k} + 1) e^{- k \cdot 3 a} & (\frac{α}{k} - 1) e^{k \cdot 3 a} \end{matrix}) (\begin{matrix} A_{3} \\ B_{3} \end{matrix}) = (\begin{matrix} e^{- k \cdot 3 a} & e^{k \cdot 3 a} \\ e^{- k \cdot 3 a} & - e^{k \cdot 3 a} \end{matrix}) (\begin{matrix} A_{4} \\ B_{4} \end{matrix}) \end{array}$

Niveles de energía

Relacionamos A₁ y B₁ con A₄ y B₄

$\begin{array}{l} (\begin{matrix} A_{1} \\ B_{1} \end{matrix}) = (M_{a}^{- 1} N_{a}) (M_{2 a}^{- 1} N_{2 a}) (M_{3 a}^{- 1} N_{3 a}) (\begin{matrix} A_{4} \\ B_{4} \end{matrix}) \\ M_{n a}^{- 1} = {(\begin{matrix} e^{- k n a} & e^{k n a} \\ (\frac{α}{k} + 1) e^{- k n a} & (\frac{α}{k} - 1) e^{k n a} \end{matrix})}^{- 1}, n = 1,2,3 \\ N_{n a} = (\begin{matrix} e^{- k n a} & e^{k n a} \\ e^{- k n a} & - e^{k n a} \end{matrix}) \end{array}$

Teniendo en cuenta, la relaciones en los extremos, en x=0 (A₁+B₁=0) y en x=4a, (A₄exp(-k·4a)+B₄exp(k·4a)=0), obtenemos la ecuación transcendente

$\begin{array}{l} (\begin{matrix} A_{1} \\ - A_{1} \end{matrix}) = (\begin{matrix} t_{11} & t_{12} \\ t_{21} & t_{22} \end{matrix}) (\begin{matrix} A_{4} \\ - A_{4} e^{- 2 k \cdot 4 a} \end{matrix}) \\ t_{11} + t_{21} - (t_{12} + t_{22}) e^{- 2 k \cdot 4 a} = 0 \end{array}$

Sea un sistema formado por un pozo de potencial de altura infinita que contiene N=3 potenciales delta de Dirac separados a=1. El parámetro α=2 de dicho potencial delta

function delta_dirac_18
    a=1;
    alfa=2;
    N=3;
    ff=@(x) niveles(x);
    xb=buscar_intervalos(ff,0.1,4,50);
    nb=size(xb);
    kr=zeros(1,nb(1));
    for m=1:nb(1)
        kr(m)=fzero(ff,[xb(m,1) xb(m,2)]);
    end
    disp(kr)
    
      %%%%%%%%%%%%
   %insertar aquí el código que representa las funciones de onda
   %%%%%%%%%%%%%

    function res=niveles(k)
        M=eye(2);
        fI=@(z) [(1-alfa/k)*exp(k*z), exp(k*z); (1+alfa/k)*exp(-k*z)
,-exp(-k*z)]/2;  
        g=@(z) [exp(-k*z), exp(k*z); exp(-k*z), -exp(k*z)];
        for s=N:-1:1
             M=(fI(s*a)*g(s*a))*M;
        end
        res=M(2,1)+M(1,1)-exp(-2*k*(N+1)*a)*(M(2,2)+M(1,2));
    end

   function xb = buscar_intervalos(f,a,b,n)
        x = a:(b-a)/n:b;
        j = 0; 
        y1=f(x(1));
        xb=[];
        for i = 1:length(x)-1
            y2=f(x(i+1));
            if sign(y1) ~= sign(y2) 
                j = j + 1;
                xb(j,1) = x(i);
                xb(j,2) = x(i+1);
            end
            y1=y2;
        end
        if isempty(xb) 
            disp('no se han encontrado cambios de signo')
        else
            disp(['número de intervalos:' int2str(j)]) 
        end
    end
end

Las raíces de la ecuación transcendente se guardan en el vector kr

    1.3352

Por debajo del valor α=0.6 aproximadamente, no hay raíces

Funciones de onda

Dados los coeficientes A₁ y B₁=-A₁, obtenemos los coeficientes A₂ y B₂, A₃ y B₃, A₄ y B₄. En forma matricial

$\begin{array}{l} (\begin{matrix} A_{2} \\ B_{2} \end{matrix}) = {(\begin{matrix} e^{- k a} & e^{k a} \\ e^{- k a} & - e^{k a} \end{matrix})}^{- 1} (\begin{matrix} e^{- k a} & e^{k a} \\ (\frac{α}{k} + 1) e^{- k a} & (\frac{α}{k} - 1) e^{k a} \end{matrix}) (\begin{matrix} A_{1} \\ B_{1} \end{matrix}) \\ (\begin{matrix} A_{3} \\ B_{3} \end{matrix}) = {(\begin{matrix} e^{- k \cdot 2 a} & e^{k \cdot 2 a} \\ e^{- k \cdot 2 a} & - e^{k \cdot 2 a} \end{matrix})}^{- 1} (\begin{matrix} e^{- i k \cdot 2 a} & e^{k \cdot 2 a} \\ (\frac{α}{k} + 1) e^{- k \cdot 2 a} & (\frac{α}{k} - 1) e^{k \cdot 2 a} \end{matrix}) (\begin{matrix} A_{2} \\ B_{2} \end{matrix}) \\ (\begin{matrix} A_{4} \\ B_{4} \end{matrix}) = {(\begin{matrix} e^{- k \cdot 3 a} & e^{k \cdot 3 a} \\ e^{- k \cdot 3 a} & - e^{k \cdot 3 a} \end{matrix})}^{- 1} (\begin{matrix} e^{- k \cdot 3 a} & e^{k \cdot 3 a} \\ (\frac{α}{k} + 1) e^{- k \cdot 3 a} & (\frac{α}{k} - 1) e^{k \cdot 3 a} \end{matrix}) (\begin{matrix} A_{3} \\ B_{3} \end{matrix}) \end{array}$

El coeficiente A₁ se determina de modo que la suma

$\begin{array}{l} \sum_{n = 1}^{N + 1} \int_{(n - 1) a}^{n a} {(A_{n} e^{- k x} + B_{n} e^{k x})}^{2} d x = 1 \\ \sum_{n = 1}^{N + 1} {\frac{B_{n}^{2}}{2 k} (e^{2 k n a} - e^{2 k (n - 1) a}) - \frac{A_{n}^{2}}{2 k} (e^{- 2 k n a} - e^{- 2 k (n - 1) a}) + 2 A_{n} B_{n} a} = 1 \end{array}$

Añadimos al script anterior, el código que representa la función de onda correspondientes al único nivel de energía

...
    A=zeros(1,N+1);
    B=zeros(1,N+1);
    A(1)=1; B(1)=-1;
    for k=kr
        f=@(z) [exp(-k*z), exp(k*z); (1+alfa/k)*exp(-k*z), -(1-alfa/k)*exp(k*z)]; 
        gI=@(z) [exp(k*z), exp(k*z); exp(-k*z), -exp(-k*z)]/2;
        suma=B(1)^2*(exp(2*k*a)-1)/(2*k)-A(1)^2*(exp(-2*k*a)-1)/(2*k)+2*A(1)*B(1)*a;
        for m=1:N
            Z=gI(m*a)*f(m*a)*[A(m);B(m)];
            A(m+1)=Z(1);
            B(m+1)=Z(2);
            suma=suma+B(m+1)^2*(exp(2*k*(m+1)*a)-exp(2*k*m*a))/(2*k)-
A(m+1)^2*(exp(-2*k*(m+1)*a)-exp(-2*k*m*a))/(2*k)+2*A(m+1)*B(m+1)*a;
        end
        hold on
         for m=0:N
             fplot(@(x) (A(m+1)*exp(-k*x)+B(m+1)*exp(k*x))/sqrt(suma),
[m*a,(m+1)*a])
        end
    end
    hold off
    grid on
    xlabel('x')
    ylabel('\Phi(x)')
    title('Función de onda')

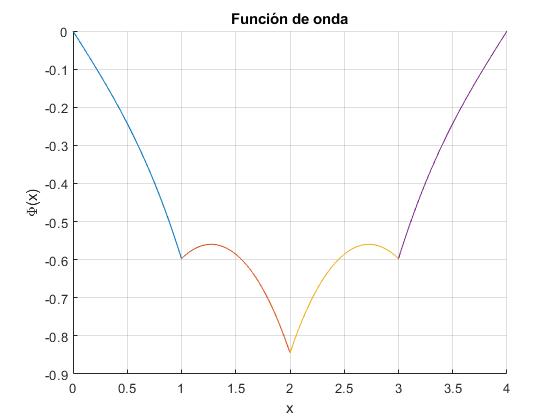
Segunda solución

Apreciaremos que la segunda solución que se describe en este apartado es mucho más simple y elegante que la primera y trabaja únicamente con valores reales

Energías E>0

Las soluciones de la ecuación de Schrödinger en las regiones I, I, III y IV con potencial V(x)=0 se pueden escribir de forma alternativa

$\begin{array}{l} \frac{d^{2} ψ}{d x^{2}} + \frac{2 m}{ℏ^{2}} E \cdot ψ = 0, E > 0 \\ \frac{d^{2} ψ}{d x^{2}} + k^{2} \cdot ψ = 0, k^{2} = \frac{2 m}{ℏ^{2}} E \\ ψ_{I} (x) = A_{1} \sin (k x) + B_{1} \cos (k x) \\ ψ_{I I} (x) = A_{2} \sin (k (x - a)) + B_{2} \cos (k (x - a)) \\ ψ_{I I I} (x) = A_{3} \sin (k (x - 2 a)) + B_{3} \cos (k (x - a)) \\ ψ_{I V} (x) = A_{4} \sin (k (x - 3 a)) + B_{4} \cos (k (x - 3 a)) \end{array}$

Condiciones en los extremos x=0, y x=4a donde V(x)=∞

$\begin{array}{l} ψ_{I} (0) = B_{1} = 0 \\ ψ_{I V} (4 a) = A_{4} \sin (k a) + B_{4} \cos (k a) = 0 \end{array}$

En en x=a, x=2a y x=3a la función de onda es continua

$\begin{array}{l} ψ_{I} (a) = ψ_{I I} (a) \\ ψ_{I I} (2 a) = ψ_{I I I} (2 a) \\ ψ_{I I I} (3 a) = ψ_{I V} (3 a) \\ {\begin{cases} A_{1} \sin (k a) + B_{1} \cos (k a) = B_{2} \\ A_{2} \sin (k a) + B_{2} \cos (k a) = B_{3} \\ A_{3} \sin (k a) + B_{3} \cos (k a) = B_{4} \end{cases} \end{array}$

La derivada primera de la función de onda NO es continua en x=a, x=2a y x=3a

Integramos la ecuación de Schrödinger en el pequeño intervalo de a-ε a a+ε

$\begin{array}{l} - \frac{ℏ^{2}}{2 m} \int_{a - ε}^{a + ε} \frac{d^{2} ψ (x)}{d x^{2}} d x - \int_{a - ε}^{a + ε} α \frac{ℏ^{2}}{2 m} δ (x - a) \cdot ψ (x) \cdot d x = E \cdot \int_{a - ε}^{a + ε} ψ (x) \cdot d x \\ - \frac{ℏ^{2}}{2 m} \lim_{ε \to 0} ({\frac{d ψ_{I I} (x)}{d x} |}_{a + ε} - {\frac{d ψ_{I} (x)}{d x} |}_{a - ε}) - α \frac{ℏ^{2}}{2 m} ψ_{I I} (a) = 0 \\ \lim_{ε \to 0} ({k A_{2} \cos (k (x - a)) - k B_{2} \sin (k (x - a)) |}_{a + ε} {- (k A_{1} \cos (k x) - B_{1} \sin (k x)) |}_{a - ε}) + α B_{2} = 0 \\ \lim_{ε \to 0} ((k A_{2} \cos (k ε) - k B_{2} \sin (k ε)) - (k A_{1} \cos (k (a - ε)) - k B_{1} \sin (k (a - ε)))) + α B_{2} = 0 \\ k A_{2} - (k A_{1} \cos (k a) - k B_{1} \sin (k a))) + α B_{2} = 0 \end{array}$

De modo similar, establecemos las otras dos ecuaciones que relacionan los coeficientes en x=2a y en x=3a

${\begin{cases} A_{1} \cos (k a) - B_{1} \sin (k a) = A_{2} + \frac{α}{k} B_{2} \\ A_{2} \cos (k a) - B_{2} \sin (k a) = A_{3} + \frac{α}{k} B_{3} \\ A_{3} \cos (k a) - B_{3} \sin (k a) = A_{4} + \frac{α}{k} B_{4} \end{cases}$

En forma matricial la relación entre los coeficientes es

$\begin{array}{l} (\begin{matrix} \sin (k a) & \cos (k a) \\ \cos (k a) & - \sin (k a) \end{matrix}) (\begin{matrix} A_{1} \\ B_{1} \end{matrix}) = (\begin{matrix} 0 & 1 \\ 1 & \frac{α}{k} \end{matrix}) (\begin{matrix} A_{2} \\ B_{2} \end{matrix}) \\ (\begin{matrix} \sin (k a) & \cos (k a) \\ \cos (k a) & - \sin (k a) \end{matrix}) (\begin{matrix} A_{2} \\ B_{2} \end{matrix}) = (\begin{matrix} 0 & 1 \\ 1 & \frac{α}{k} \end{matrix}) (\begin{matrix} A_{3} \\ B_{3} \end{matrix}) \\ (\begin{matrix} \sin (k a) & \cos (k a) \\ \cos (k a) & - \sin (k a) \end{matrix}) (\begin{matrix} A_{3} \\ B_{3} \end{matrix}) = (\begin{matrix} 0 & 1 \\ 1 & \frac{α}{k} \end{matrix}) (\begin{matrix} A_{4} \\ B_{4} \end{matrix}) \end{array}$

Niveles de energía

El resultado de la relación entre A₁, B₁ y A₄ y B₄ es el producto de seis matrices

$\begin{array}{l} (\begin{matrix} A_{1} \\ B_{1} \end{matrix}) = {(M^{- 1} N)}^{3} (\begin{matrix} A_{4} \\ B_{4} \end{matrix}) \\ M^{- 1} = {(\begin{matrix} \sin (k a) & \cos (k a) \\ \cos (k a) & - \sin (k a) \end{matrix})}^{- 1} = (\begin{matrix} \sin (k a) & \cos (k a) \\ \cos (k a) & - \sin (k a) \end{matrix}) \\ N = (\begin{matrix} 0 & 1 \\ 1 & \frac{α}{k} \end{matrix}) \end{array}$

Teniendo en cuenta, la relaciones en los extremos, en x=0 (B₁=0) y en x=4a, (A₄sin(ka)+B₄cos(ka)=0), obtenemos la ecuación transcendente

$\begin{array}{l} (\begin{matrix} A_{1} \\ 0 \end{matrix}) = (\begin{matrix} t_{11} & t_{12} \\ t_{21} & t_{22} \end{matrix}) (\begin{matrix} A_{4} \\ - A_{4} \frac{\sin (k a)}{\cos (k a)} \end{matrix}) \\ t_{21} \cos (k a) - t_{22} \sin (k a) = 0 \end{array}$

Sea un sistema formado por un pozo de potencial de altura infinita que contiene N=3 potenciales delta de Dirac separados a=1. El parámetro α=0.5 de dicho potencial delta

function delta_dirac_20
    a=1;
    alfa=0.5;
    N=3;
    ff=@(x) niveles(x);
    xb=buscar_intervalos(ff,0.1,4,50);
    nb=size(xb);
    kr=zeros(1,nb(1));
    for m=1:nb(1)
        kr(m)=fzero(ff,[xb(m,1) xb(m,2)]);
    end
    disp(kr)
 
   %%%%%%%%%%%%
   %insertar aquí el código que representa las funciones de onda
   %%%%%%%%%%%%%
 
    function res=niveles(k)
        T=eye(2);
        M=[0,1; 1,alfa/k];  
        MI=[sin(k*a),cos(k*a);cos(k*a),-sin(k*a)];
       for s=N:-1:1
            T=(MI*M)*T;
        end
        res=T(2,1)*cos(k*a)-T(2,2)*sin(k*a);
    end

   function xb = buscar_intervalos(f,a,b,n)
        x = a:(b-a)/n:b;
        j = 0; 
        y1=f(x(1));
        xb=[];
        for i = 1:length(x)-1
            y2=f(x(i+1));
            if sign(y1) ~= sign(y2) 
                j = j + 1;
                xb(j,1) = x(i);
                xb(j,2) = x(i+1);
            end
            y1=y2;
        end
        if isempty(xb) 
            disp('no se han encontrado cambios de signo')
        else
            disp(['número de intervalos:' int2str(j)]) 
        end
    end
end

Las raíces de la ecuación transcendente se guardan en el vector kr. Obtenemos los mismos valores que en el apartado anterior, con una menor complejidad cálculo

    0.3070    1.3930    2.2390    3.1420    3.8640

Funciones de onda

Dados los coeficientes A₁ y B₁=0, obtenemos los coeficientes A₂ y B₂, A₃ y B₃, A₄ y B₄. En forma matricial

$\begin{array}{l} (\begin{matrix} A_{2} \\ B_{2} \end{matrix}) = {(\begin{matrix} 0 & 1 \\ 1 & \frac{α}{k} \end{matrix})}^{- 1} (\begin{matrix} \sin (k a) & \cos (k a) \\ \cos (k a) & - \sin (k a) \end{matrix}) (\begin{matrix} A_{1} \\ B_{1} \end{matrix}) \\ (\begin{matrix} A_{3} \\ B_{3} \end{matrix}) = {(\begin{matrix} 0 & 1 \\ 1 & \frac{α}{k} \end{matrix})}^{- 1} (\begin{matrix} \sin (k a) & \cos (k a) \\ \cos (k a) & - \sin (k a) \end{matrix}) (\begin{matrix} A_{2} \\ B_{2} \end{matrix}) \\ (\begin{matrix} A_{4} \\ B_{4} \end{matrix}) = {(\begin{matrix} 0 & 1 \\ 1 & \frac{α}{k} \end{matrix})}^{- 1} (\begin{matrix} \sin (k a) & \cos (k a) \\ \cos (k a) & - \sin (k a) \end{matrix}) (\begin{matrix} A_{3} \\ B_{3} \end{matrix}) \\ {(\begin{matrix} 0 & 1 \\ 1 & \frac{α}{k} \end{matrix})}^{- 1} = (\begin{matrix} - \frac{α}{k} & 1 \\ 1 & 0 \end{matrix}) \end{array}$

El coeficiente A₁ se determina de modo que la suma

$\begin{array}{l} \sum_{n = 1}^{N + 1} \int_{(n - 1) a}^{n a} {(A_{n} \sin (k (x - (n - 1) a)) + B_{n} \cos (k (x - (n - 1) a)))}^{2} d x = 1 \\ \sum_{n = 1}^{N + 1} {\frac{A_{n}^{2}}{2} (a - \frac{\sin (2 k a)}{2 k}) + \frac{B_{n}^{2}}{2} (a + \frac{\sin (2 k a)}{2 k}) - \frac{A_{n} B_{n}}{2 k} (\cos (2 k a) - 1)} = 1 \end{array}$

Añadimos al script anterior el código que representa las funciones de onda correspondientes a los tres primeros niveles de energía

...
    A=zeros(1,N+1);
    B=zeros(1,N+1);
    A(1)=1; B(1)=0;
    for k=kr(1:3)
        MI=[-alfa/k,1;1,0];  
        M=[sin(k*a),cos(k*a);cos(k*a),-sin(k*a)];
        suma=A(1)^2*(a-sin(2*k*a)/(2*k))/2+B(1)^2*(a+sin(2*k*a)/(2*k))/2
-A(1)*B(1)*(cos(2*k*a)-1)/(2*k);
        for m=1:N
            Z=(MI*M)*[A(m);B(m)];
            A(m+1)=Z(1);
            B(m+1)=Z(2);
            suma=suma+A(m+1)^2*(a-sin(2*k*a)/(2*k))/2+B(m+1)^2*(a+sin(2*k*a)
/(2*k))/2-A(m+1)*B(m+1)*(cos(2*k*a)-1)/(2*k);
        end
        hold on
        for m=0:N
            fplot(@(x) (A(m+1)*sin(k*(x-m*a))+B(m+1)*cos(k*(x-m*a)))
/sqrt(suma),[m*a,(m+1)*a])
        end
    end
    hold off
    grid on
    xlabel('x')
    ylabel('\Phi(x)')
    title('Funciones de onda')

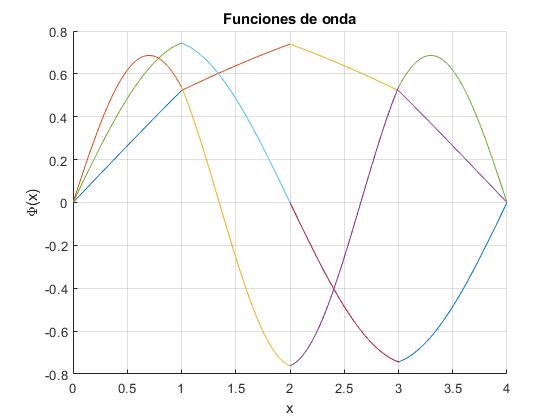
Una figura similar hemos obtenido en el apartado anteror, pero invertida

Energías E<0

Las soluciones de la ecuación de Schrödinger en las regiones I, I, III y IV con potencial V(x)=0 son

$\begin{array}{l} \frac{d^{2} ψ}{d x^{2}} + \frac{2 m}{ℏ^{2}} E \cdot ψ = 0, E < 0 \\ \frac{d^{2} ψ}{d x^{2}} - k^{2} \cdot ψ = 0, k^{2} = - \frac{2 m}{ℏ^{2}} E \\ ψ_{I} (x) = A_{1} \exp (- k x) + B_{1} \exp (k x) \\ ψ_{I I} (x) = A_{2} \exp (- k (x - a)) + B_{2} \exp (- k (x - a)) \\ ψ_{I I I} (x) = A_{3} \exp (- k (x - 2 a)) + B_{3} \exp (- k (x - 2 a)) \\ ψ_{I V} (x) = A_{4} \exp (- k (x - 3 a)) + B_{4} \exp (- k (x - 3 a)) \end{array}$

Condiciones en los extremos x=0, y x=4a donde V(x)=∞

$\begin{array}{l} ψ_{I} (0) = A_{1} + B_{1} = 0 \\ ψ_{I V} (4 a) = A_{4} \exp (- k a) + B_{4} \exp (k a) = 0 \end{array}$

En en x=a, x=2a y x=3a la función de onda es continua

$\begin{array}{l} ψ_{I} (a) = ψ_{I I} (a) \\ ψ_{I I} (2 a) = ψ_{I I I} (2 a) \\ ψ_{I I I} (3 a) = ψ_{I V} (3 a) \\ {\begin{cases} A_{1} \exp (- k a) + B_{1} \exp (k a) = A_{2} + B_{2} \\ A_{2} \exp (- k a) + B_{2} \exp (k a) = A_{3} + B_{3} \\ A_{3} \exp (- k a) + B_{3} \exp (k a) = A_{4} + B_{4} \end{cases} \end{array}$

La derivada primera de la función de onda NO es continua en x=a, x=2a y x=3a

Integramos la ecuación de Schrödinger en el pequeño intervalo de a-ε a a+ε

$\begin{array}{l} - \frac{ℏ^{2}}{2 m} \int_{a - ε}^{a + ε} \frac{d^{2} ψ (x)}{d x^{2}} d x - \int_{a - ε}^{a + ε} α \frac{ℏ^{2}}{2 m} δ (x - a) \cdot ψ (x) \cdot d x = E \cdot \int_{a - ε}^{a + ε} ψ (x) \cdot d x \\ - \frac{ℏ^{2}}{2 m} \lim_{ε \to 0} ({\frac{d ψ_{I I} (x)}{d x} |}_{a + ε} - {\frac{d ψ_{I} (x)}{d x} |}_{a - ε}) - α \frac{ℏ^{2}}{2 m} ψ_{I I} (a) = 0 \\ \lim_{ε \to 0} ({- k A_{2} \exp (- k (x - a)) + k B_{2} \exp (k (x - a)) |}_{a + ε} {- (- k A_{1} \exp (- k x) + k B_{1} \exp (k x)) |}_{a - ε}) + α (A_{2} + B_{2}) = 0 \\ \lim_{ε \to 0} ((- k A_{2} \exp (- k ε) + k B_{2} \exp (k ε)) - (- k A_{1} \exp (- k (a - ε)) + k B_{1} \exp (k (a - ε)))) + α (A_{2} + B_{2}) = 0 \\ (- k A_{2} + k B_{2}) - (- k A_{1} \exp (- k a) + k B_{1} \exp (k a)) + α (A_{2} + B_{2}) = 0 \end{array}$

De modo similar, establecemos las otras dos ecuaciones que relacionan los coeficientes en x=2a y en x=3a

${\begin{cases} A_{1} \exp (- k a) - B_{1} \exp (k a) = (1 - \frac{α}{k}) A_{2} - (1 + \frac{α}{k}) B_{2} \\ A_{2} \exp (- k a) - B_{2} \exp (k a) = (1 - \frac{α}{k}) A_{3} - (1 + \frac{α}{k}) B_{3} \\ A_{3} \exp (- k a) - B_{3} \exp (k a) = (1 - \frac{α}{k}) A_{4} - (1 + \frac{α}{k}) B_{4} \end{cases}$

En forma matricial la relación entre los coeficientes es

$\begin{array}{l} (\begin{matrix} e^{- k a} & e^{k a} \\ e^{- k a} & - e^{k a} \end{matrix}) (\begin{matrix} A_{1} \\ B_{1} \end{matrix}) = (\begin{matrix} 1 & 1 \\ (1 - \frac{α}{k}) & - (1 + \frac{α}{k}) \end{matrix}) (\begin{matrix} A_{2} \\ B_{2} \end{matrix}) \\ (\begin{matrix} e^{- k a} & e^{k a} \\ e^{- k a} & - e^{k a} \end{matrix}) (\begin{matrix} A_{2} \\ B_{2} \end{matrix}) = (\begin{matrix} 1 & 1 \\ (1 - \frac{α}{k}) & - (1 + \frac{α}{k}) \end{matrix}) (\begin{matrix} A_{3} \\ B_{3} \end{matrix}) \\ (\begin{matrix} e^{- k a} & e^{k a} \\ e^{- k a} & - e^{k a} \end{matrix}) (\begin{matrix} A_{3} \\ B_{3} \end{matrix}) = (\begin{matrix} 1 & 1 \\ (1 - \frac{α}{k}) & - (1 + \frac{α}{k}) \end{matrix}) (\begin{matrix} A_{4} \\ B_{4} \end{matrix}) \end{array}$

Niveles de energía

Relacionamos A₁ y B₁ con A₄ y B₄

$\begin{array}{l} (\begin{matrix} A_{1} \\ B_{1} \end{matrix}) = {(M^{- 1} N)}^{3} (\begin{matrix} A_{4} \\ B_{4} \end{matrix}) \\ M^{- 1} = {(\begin{matrix} e^{- k a} & e^{k a} \\ e^{- k a} & - e^{k a} \end{matrix})}^{- 1} = \frac{1}{2} (\begin{matrix} e^{k a} & e^{k a} \\ e^{- k a} & - e^{- k a} \end{matrix}) \\ N = (\begin{matrix} 1 & 1 \\ (1 - \frac{α}{k}) & - (1 + \frac{α}{k}) \end{matrix}) \end{array}$

Teniendo en cuenta, la relaciones en los extremos, en x=0 (A₁+B₁=0) y en x=4a, (A₄exp(-ka)+B₄exp(ka)=0), obtenemos la ecuación transcendente

$\begin{array}{l} (\begin{matrix} A_{1} \\ - A_{1} \end{matrix}) = (\begin{matrix} t_{11} & t_{12} \\ t_{21} & t_{22} \end{matrix}) (\begin{matrix} A_{4} \\ - A_{4} e^{- 2 k a} \end{matrix}) \\ t_{11} + t_{21} - (t_{12} + t_{22}) e^{- 2 k a} = 0 \end{array}$

Sea un sistema formado por un pozo de potencial de altura infinita que contiene N=3 potenciales delta de Dirac separados a=1. El parámetro α=2 de dicho potencial delta

function delta_dirac_21
    a=1;
    alfa=2;
    N=3;
    ff=@(x) niveles(x);
    xb=buscar_intervalos(ff,0.1,4,50);
    nb=size(xb);
    kr=zeros(1,nb(1));
    for m=1:nb(1)
        kr(m)=fzero(ff,[xb(m,1) xb(m,2)]);
    end
    disp(kr)
  
  %%%%%%%%%%%%
   %insertar aquí el código que representa las funciones de onda
   %%%%%%%%%%%%%
 
    function res=niveles(k)
        T=eye(2);
        M=[1,1; 1-alfa/k,-1-alfa/k];  
        MI=[exp(k*a),exp(k*a);exp(-k*a),-exp(-k*a)]/2;
        for s=N:-1:1
            T=(MI*M)*T;
        end
        res=T(1,1)+T(2,1)-(T(1,2)+T(2,2))*exp(-2*k*a);
    end

   function xb = buscar_intervalos(f,a,b,n)
        x = a:(b-a)/n:b;
        j = 0; 
        y1=f(x(1));
        xb=[];
        for i = 1:length(x)-1
            y2=f(x(i+1));
            if sign(y1) ~= sign(y2) 
                j = j + 1;
                xb(j,1) = x(i);
                xb(j,2) = x(i+1);
            end
            y1=y2;
        end
        if isempty(xb) 
            disp('no se han encontrado cambios de signo')
        else
            disp(['número de intervalos:' int2str(j)]) 
        end
    end
end

Las raíces de la ecuación transcendente se guardan en el vector kr. El mismo valor que obtuvimos en el primer apartado E<0

    1.3352

Funciones de onda

Dados los coeficientes A₁ y B₁=-A₁, obtenemos los coeficientes A₂ y B₂, A₃ y B₃, A₄ y B₄. En forma matricial

$\begin{array}{l} (\begin{matrix} A_{2} \\ B_{2} \end{matrix}) = {(\begin{matrix} 1 & 1 \\ (1 - \frac{α}{k}) & - (1 + \frac{α}{k}) \end{matrix})}^{- 1} (\begin{matrix} e^{- k a} & e^{k a} \\ e^{- k a} & - e^{k a} \end{matrix}) (\begin{matrix} A_{1} \\ B_{1} \end{matrix}) \\ (\begin{matrix} A_{3} \\ B_{3} \end{matrix}) = {(\begin{matrix} 1 & 1 \\ (1 - \frac{α}{k}) & - (1 + \frac{α}{k}) \end{matrix})}^{- 1} (\begin{matrix} e^{- k a} & e^{k a} \\ e^{- k a} & - e^{k a} \end{matrix}) (\begin{matrix} A_{2} \\ B_{2} \end{matrix}) \\ (\begin{matrix} A_{4} \\ B_{4} \end{matrix}) = {(\begin{matrix} 1 & 1 \\ (1 - \frac{α}{k}) & - (1 + \frac{α}{k}) \end{matrix})}^{- 1} (\begin{matrix} e^{- k a} & e^{k a} \\ e^{- k a} & - e^{k a} \end{matrix}) (\begin{matrix} A_{3} \\ B_{3} \end{matrix}) \\ {(\begin{matrix} 1 & 1 \\ (1 - \frac{α}{k}) & - (1 + \frac{α}{k}) \end{matrix})}^{- 1} = \frac{1}{2} (\begin{matrix} (1 + \frac{α}{k}) & 1 \\ (1 - \frac{α}{k}) & - 1 \end{matrix}) \end{array}$

El coeficiente A₁ se calcula de modo que la suma

$\begin{array}{l} \sum_{n = 1}^{N + 1} \int_{(n - 1) a}^{n a} {(A_{n} \exp (- k (x - (n - 1) a)) + B_{n} \exp (k (x - (n - 1) a)))}^{2} d x = 1 \\ \sum_{n = 1}^{N + 1} {- \frac{A_{n}^{2}}{2 k} (e^{- 2 k a} - 1) + \frac{B_{n}^{2}}{2 k} (e^{2 k a} - 1) + 2 A_{n} B_{n} a} = 1 \end{array}$

Añadimos al script anterior el código que representa la función de onda correspondiente al único nivel de energía

...
    A=zeros(1,N+1);
    B=zeros(1,N+1);
    A(1)=1; B(1)=-1;
    for k=kr
        MI=[1+alfa/k,1;1-alfa/k,-1]/2;  
        M=[exp(-k*a),exp(k*a);exp(-k*a),-exp(k*a)];
        suma=-A(1)^2*(exp(-2*k*a)-1)/(2*k)+B(1)^2*(exp(2*k*a)-1)/(2*k)+
2*A(1)*B(1)*a;
        for m=1:N
            Z=(MI*M)*[A(m);B(m)];
            A(m+1)=Z(1);
            B(m+1)=Z(2);
            suma=suma-A(m+1)^2*(exp(-2*k*a)-1)/(2*k)+B(m+1)^2*(exp(2*k*a)-1)
/(2*k)+2*A(m+1)*B(m+1)*a;
        end
        hold on
         for m=0:N
            fplot(@(x) (A(m+1)*exp(-k*(x-m*a))+B(m+1)*exp(k*(x-m*a)))
/sqrt(suma),[m*a,(m+1)*a])
        end
    end
    hold off
    grid on
    grid on
    xlabel('x')
    ylabel('\Phi(x)')
    title('Función de onda')

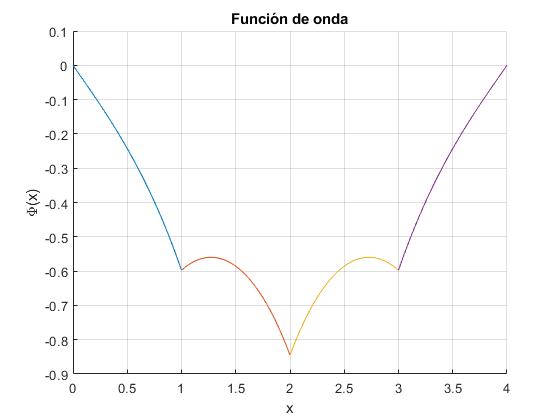
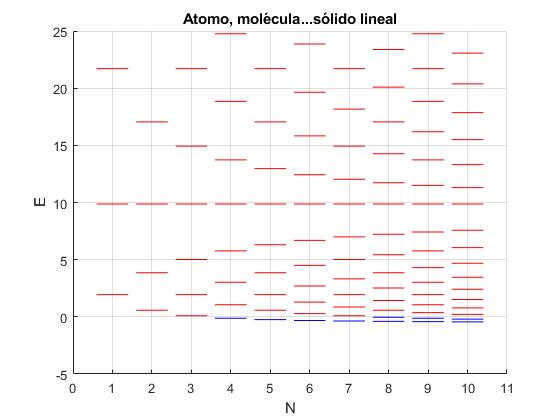
Niveles de energía de un sistema de N potenciales delta

Para E>0 la energía E es proporcional a k²
Para E<0 la energía E es proporcional a -k²

Representamos los niveles de energía para sistemas de N=1,2,3...10, pozos de potencial delta de Dirac

El parámetro α=0.5

function delta_dirac_22
    a=1;
    alfa=2; %parámetro
    for N=1:10 %número de potenciales delta
        ff=@(x) niveles_sup(x); %para E>0
        xb=buscar_intervalos(ff,0.1,5,50);
        nb=size(xb);
        ks=zeros(1,nb(1));
        for m=1:nb(1)
            ks(m)=fzero(ff,[xb(m,1) xb(m,2)]);
    	end
        ff=@(x) niveles_inf(x); %para E<0
        xb=buscar_intervalos(ff,0.1,5,50);
        nb=size(xb);
        ki=zeros(1,nb(1));
        for m=1:nb(1)
            ki(m)=fzero(ff,[xb(m,1) xb(m,2)]);
        end
%niveles
        for i=1:length(ks)  %para E>0
            line([N-0.4 N+0.4],[ks(i)^2, ks(i)^2], 'color','r')
        end
        for i=1:length(ki)  %para E<0
            line([N-0.4 N+0.4],[-ki(i)^2, -ki(i)^2], 'color','b')
        end
    end
    grid on
    xlim([0,11])
    xlabel('N');
    ylabel('E')
    title('Atomo, molécula...sólido lineal')

    function res=niveles_inf(k) %para E<0
        T=eye(2);
        M=[1,1; 1-alfa/k,-1-alfa/k];  
        MI=[exp(k*a),exp(k*a);exp(-k*a),-exp(-k*a)]/2;
       for s=N:-1:1
             T=(MI*M)*T;
        end
        res=T(1,1)+T(2,1)-(T(1,2)+T(2,2))*exp(-2*k*a);
    end

    function res=niveles_sup(k) %para E>0
        T=eye(2);
        M=[0,1; 1,alfa/k];  
        MI=[sin(k*a),cos(k*a);cos(k*a),-sin(k*a)];
        for s=N:-1:1
            T=(MI*M)*T;
        end
        res=T(2,1)*cos(k*a)-T(2,2)*sin(k*a);
    end

   function xb = buscar_intervalos(f,a,b,n)
        x = a:(b-a)/n:b;
        j = 0; 
        y1=f(x(1));
        xb=[];
        for i = 1:length(x)-1
            y2=f(x(i+1));
            if sign(y1) ~= sign(y2) 
                j = j + 1;
                xb(j,1) = x(i);
                xb(j,2) = x(i+1);
            end
            y1=y2;
        end
        if isempty(xb) 
            disp('no se han encontrado cambios de signo')
        else
            disp(['número de intervalos:' int2str(j)]) 
        end
    end
end

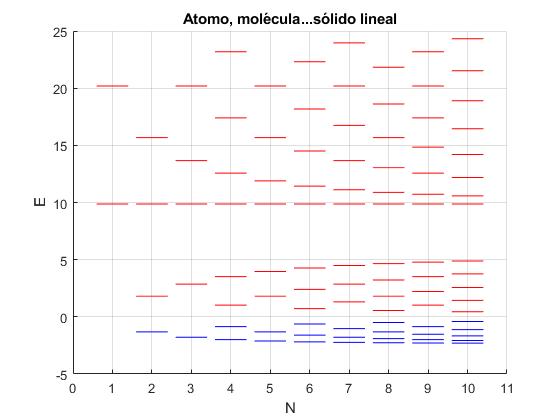
El parámetro α=2

Referencias

Todd K. Timberlake, Neilson Woodfield. Band formation and defects in a finite periodic quantum potential. Am. J. Phys. 90 (2), February 2022. pp. 93-102