Barrera de potencial delta de Dirac

Consideremos ahora un pozo de potencial de altura infinita y anchura 2a, con una barrera de potencial delta de Dirac centrada en el origen.

Representamos el potencial delta de Dirac por la función que se muestra en la figura, una barrera de anchura 2ε y altura que tiende a infinito, siendo ε→0.

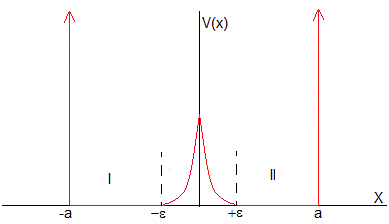
Dividimos el intervalo (-a, a) en tres regiones

${\displaystyle V(x)\{\begin{array}{l}\infty ,x\le -a\\ -\alpha \frac{{\hslash }^2}{2m}\delta (x),-a<x<a\\ \infty ,x\ge a\end{array}}$

• Región I,

${\displaystyle \begin{array}{l}\frac{d^2\psi }{d{x}^2}+\frac{2m}{{\hslash }^2}E·\psi =\mathrm{0,}E>0\\ \frac{d^2\psi }{d{x}^2}+k^2·\psi =\mathrm{0,}{k}^2=\frac{2m}{{\hslash }^2}E\\ {\psi }_I(x)=A\exp (-ikx)+B\exp (ikx)\end{array}}$

En x=-a el potencial es infinito

${\displaystyle \begin{array}{l}{\psi }_I(-a)=0\\ A\exp (ika)+B\exp (-ika)=0\end{array}}$

• Región II,

${\displaystyle \begin{array}{l}\frac{d^2\psi }{d{x}^2}+k^2·\psi =\mathrm{0,}{k}^2=\frac{2m}{{\hslash }^2}E\\ {\psi }_{II}(x)=C\exp (-ikx)+D\exp (ikx)\end{array}}$

En x=a el potencial es infinito

${\displaystyle \begin{array}{l}{\psi }_{II}(a)=0\\ C\exp (-ika)+D\exp (ika)=0\end{array}}$

Niveles de energía

• La función de onda es continua en x=0

${\displaystyle \begin{array}{l}{\psi }_I(0)={\psi }_{II}(0)\\ A+B=C+D\end{array}}$

• La derivada primera de la función de onda NO es continua en x=0

Integramos la ecuación de Schrödinger en el pequeño intervalo de -ε, +ε

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}{\displaystyle \underset{-\epsilon }{\overset{\epsilon }{\int }}\frac{d^2\psi (x)}{d{x}^2}}dx+{\displaystyle \underset{-\epsilon }{\overset{\epsilon }{\int }}\alpha \frac{{\hslash }^2}{2m}\delta (x)·\psi (x)·dx}=E·{\displaystyle \underset{-\epsilon }{\overset{\epsilon }{\int }}\psi (x)·dx}\\ -\frac{{\hslash }^2}{2m}\underset{\epsilon \to 0}{\lim }\left({\frac{d{\psi }_{II}(x)}{dx}|}_{\epsilon }-{\frac{d{\psi }_I(x)}{dx}|}_{-\epsilon }\right)+\alpha \frac{{\hslash }^2}{2m}\psi (0)=0\\ \underset{\epsilon \to 0}{\lim }\left({-ikC\exp (-ikx)+ikD\exp (ikx)|}_{\epsilon }{-\left(-ikA\exp (-ikx)+ikB\exp (ikx)\right)|}_{-\epsilon }\right)=\alpha \left(A+B\right)\\ \underset{\epsilon \to 0}{\lim }\left(\left(-ikC\exp (-ik\epsilon )+ikD\exp (ik\epsilon )\right)-\left(-ikA\exp (ik\epsilon )+ikB\exp (-ik\epsilon )\right)\right)=\alpha \left(A+B\right)\\ \left(-ikC+ikD\right)-\left(-ikA+ikB\right)=\alpha \left(A+B\right)\\ \left(1-\frac{\alpha }{ik}\right)A-\left(1+\frac{\alpha }{ik}\right)B=C-D\end{array}}$

Despejamos los coeficientes C y D del sistema

${\displaystyle \begin{array}{l}\{\begin{array}{l}A+B=C+D\\ \left(1-\frac{\alpha }{ik}\right)A-\left(1+\frac{\alpha }{ik}\right)B=C-D\end{array}\\ \left(2-\frac{\alpha }{ik}\right)A-\frac{\alpha }{ik}B=2C\\ \frac{\alpha }{ik}A+\left(2+\frac{\alpha }{ik}\right)B=2D\end{array}}$

Utilizamos las relaciones entre A y B en el extremo -a y las relaciones entre C y D en el extremo a

${\displaystyle \{\begin{array}{l}B=-A\exp (2ika)\\ D=-C\exp (-2ika)\end{array}}$

Llegamos a la ecuación en k

${\displaystyle \begin{array}{l}\frac{\alpha }{ik}-\left(2+\frac{\alpha }{ik}\right)e^{2ika}+\left\{\left(2-\frac{\alpha }{ik}\right)+\frac{\alpha }{ik}{e}^{2ika}\right\}{e}^{-2ika}\\ \frac{\alpha }{k}\cos (2ka)-2\sin (2ka)=\frac{\alpha }{k}\\ \sin (ka)\left(\frac{\alpha }{k}\sin (ka)+2\cos (ka)\right)=0\\ \{\begin{array}{l}\sin (ka)=\mathrm{0,}ka=n\pi ,n=\mathrm{1,2,3...}\\ \alpha \sin (ka)+2k\cos (ka)=0\end{array}\end{array}}$

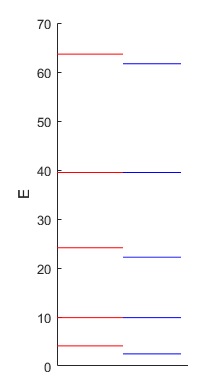
En la figura, se muestran en color azul, los niveles de energía de un pozo de potencial de altura infinita y de anchura 2a=2·1. Cuando se introduce en el origen un pozo de potencial delta de Dirac cuyo parámetro α=2, los niveles pares no cambian, los impares incrementan ligeramente la energía (en color rojo)

El código para representar los niveles es

function delta_dirac_15
    alfa=2; %parámetro
    a=1; %anchura pozo 2a
    f=@(x) alfa*sin(x*a)+2*x.*cos(x*a);
    %niveles de energía
    x=linspace(0,20,40);
    r1=raices(f,x); 
    r2=(1:length(r1))*pi/a;
    rr=sort([r1,r2]); %ordena los valores k de los niveles de menor a mayor
    disp(rr)
    
    %funciones de onda
    for n=1:5
        E=(n*pi/(2*a))^2; %pozo de potencial de altura infinita
        line([1,2],[E,E], 'color','b')
        E=rr(n)^2; %pozo de potencial con delta de Dirac
        line([0,1],[E,E],'color','r')
    end
    xlabel('x')
    ylabel('E')
    title('Niveles de energía')
    
    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

2.0288    3.1416    4.9132    6.2832    7.9787     9.4248   
11.0855   12.5664   14.2074   15.7080   17.3364    18.8496

Funciones de onda

• Función de onda antisimétrica

Los niveles pares 2, 4, 6... corresponden a funciones de onda antisimétricas, se obtienen de la ecuación sin(ka)=0, ka=nπ

${\displaystyle \begin{array}{l}\left(2-\frac{\alpha }{ik}\right)A-\frac{\alpha }{ik}B=2C\\ \left(2-\frac{\alpha }{ik}\right)A-\frac{\alpha }{ik}\left(-A\exp (2ika)\right)=2C\\ \left(2-\frac{\alpha }{ik}\right)A+\frac{\alpha }{ik}A\left(\cos (2ka)+i\sin (2ka)\right)=2C\\ \left(2-\frac{\alpha }{ik}\right)A+\frac{\alpha }{ik}A\left(\left({\cos }^2(ka)-{\sin }^2(ka)\right)+2i\sin (ka)\cos (ka)\right)=2C\\ \left(2-\frac{\alpha }{ik}\right)A+\frac{\alpha }{ik}A=2C,\\ A=C\end{array}}$

De la relación A+B=C+D, obtenemos B=D

De la relación

${\displaystyle \begin{array}{l}A\exp (ika)+B\exp (-ika)=0\\ \left(A+B\right)\cos (ka)=\mathrm{0,}A=-B\end{array}}$

Finalmente, C=-D

Calculamos el coeficiente A de modo que

${\displaystyle \begin{array}{l}\{\begin{array}{l}{\psi }_I(x)=A\exp (-ikx)+B\exp (ikx),-a<x<0\\ {\psi }_{II}(x)=C\exp (-ikx)+D\exp (ikx),0<x<a\end{array}\\ {\displaystyle \underset{-a}{\overset{0}{\int }}{\left|{\psi }_I(x)\right|}^{2}dx}+{\displaystyle \underset{0}{\overset{a}{\int }}{\left|{\psi }_{II}(x)\right|}^{2}dx=1}\end{array}}$

Teniendo en cuenta la relación entre los coeficientes A=-B, C=-D, A=C

${\displaystyle \{\begin{array}{l}{\psi }_I(x)=2iA\sin (kx),-a<x<0\\ {\psi }_{II}(x)=2iA\sin (kx),0<x<a\end{array}}$

Designando a 2iA como coeficiente A

${\displaystyle \begin{array}{l}{\displaystyle \underset{-a}{\overset{0}{\int }}{A}^2{\sin }^2(kx)dx}+{\displaystyle \underset{0}{\overset{a}{\int }}{A}^2{\sin }^2(kx)dx}=1\\ {\displaystyle \underset{-a}{\overset{a}{\int }}{A}^2{\sin }^2(kx)dx}=1\\ A^2\left(a-\frac{1}{2k}\sin (2ka)\right)=\mathrm{1,}A=\frac{1}{\sqrt{a}}\\ \psi (x)=\frac{1}{\sqrt{a}}\sin (kx),-a<x<a\end{array}}$

• Función de onda simétrica

Los niveles impares 1, 3, 5... corresponden a funciones de onda simétricas, se obtienen de la ecuación transcendente, αsin(ka)+2kcos(ka)=0

Partimos de la relación

${\displaystyle \left(2-\frac{\alpha }{ik}\right)A+\frac{\alpha }{ik}A\left(\left({\cos }^2(ka)-{\sin }^2(ka)\right)+2i\sin (ka)\cos (ka)\right)=2C}$

Utilizamos las relaciones trigonométricas

${\displaystyle \sin \theta =\frac{\tan \theta }{\sqrt{1+{\tan }^2\theta }},\cos \theta =\frac{1}{\sqrt{1+{\tan }^2\theta }}}$

Haciendo operaciones y simplificando, llegamos a

${\displaystyle \begin{array}{l}\left(2-\frac{\alpha }{ik}\right)A+\frac{\alpha }{ik}\left(\frac{{\alpha }^2}{{\alpha }^2+4k^2}-\frac{4k^2}{{\alpha }^2+4k^2}+2i\frac{-2k\alpha }{{\alpha }^2+4k^2}\right)A=2C\\ C=\frac{{\left(2k+\alpha i\right)}^2}{4k^2+{\alpha }^2}A\\ C{C}^{*}=\frac{{\left(2k+\alpha i\right)}^2{\left(2k-\alpha i\right)}^2}{{\left(4k^2+{\alpha }^2\right)}^2}{A}^2=\frac{{\left(4k^2+{\alpha }^2\right)}^2}{{\left(4k^2+{\alpha }^2\right)}^2}{A}^2=A^2\end{array}}$

Conocido el coeficiente C en función de A, los coeficientes B y D, como se ha demostrado, valen

${\displaystyle \begin{array}{l}B=-A\exp (2ika)\\ D=-C\exp (-2ika)\end{array}}$

Determinamos el coeficiente A de modo que

${\displaystyle \begin{array}{l}{\displaystyle \underset{-a}{\overset{0}{\int }}\left(A{e}^{-ikx}+B{e}^{ikx}\right)\left(A{e}^{ikx}+B^{*}{e}^{-ikx}\right)dx}+{\displaystyle \underset{0}{\overset{a}{\int }}\left(C{e}^{-ikx}+D{e}^{ikx}\right)\left(C^{*}{e}^{ikx}+D^{*}{e}^{-ikx}\right)dx}=1\\ \left(A^2+B{B}^{*}\right)a+\frac{AB}{2ik}\left(1-e^{-2ika}\right)-\frac{A{B}^{*}}{2ik}\left(1-e^{2ika}\right)+\left(C{C}^{*}+D{D}^{*}\right)a-\frac{C{D}^{*}}{2ik}\left(e^{-2ika}-1\right)+\frac{D{C}^{*}}{2ik}\left(e^{2ika}-1\right)=1\\ 2A^{2}a-\frac{A^2}{k}\sin (2ka)+2C{C}^{*}a-\frac{C{C}^{*}}{k}\sin (2ka)=1\\ 2A^{2}a-\frac{A^2}{k}\sin (2ka)+2A^{2}a-\frac{A^2}{k}\sin (2ka)=1\\ A^2\left(4a-\frac{2}{k}\sin (2ka)\right)=1\\ A^2\left(4a-\frac{4}{k}\sin (ka)\cos (ka)\right)=1\\ 2A^2\left(2a+\frac{\alpha }{k^2}{\sin }^2(ka)\right)=1\end{array}}$

Representamos las funciones de onda correspondientes al primer nivel (estado fundamental), n=1, segundo, n=2 y tercero, n=3, para un pozo de potencial de altura infinita y de anchura 2a=2·1, que contiene una barrera de potencial, delta de Dirac, de parámetro α=2, situada en su punto medio (origen)

function delta_dirac_14
    alfa=2;
    a=1;
    f=@(x) alfa*sin(x*a)+2*x.*cos(x*a);
    x=linspace(0,20,40);
    r1=raices(f,x); 
    r2=(1:length(r1))*pi/a;
    rr=sort([r1,r2]);
    n=1; %nivel de energía
    k=rr(n); 
    hold on
    if rem(n,2)==0
        fplot(@(x) sin(k*x)/sqrt(a),[-a,a])
    else
        A=1/sqrt(2*(2*a+alfa*sin(k*a)^2/k^2)); 
        C=(2*k+1i*alfa)^2*A/(4*k^2+alfa^2);
        B=-A*exp(2*1i*k*a);
        D=-C*exp(-2*1i*k*a);
        fplot(@(x) real(A*exp(-1i*k*x)+B*exp(1i*k*x)),[-a,0])
        fplot(@(x) real(C*exp(-1i*k*x)+D*exp(1i*k*x)),[0,a])           
    end
    hold off
   grid on
   xlabel('x')
   ylabel('\Phi(x)')
   title('Función de onda')
    
     function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

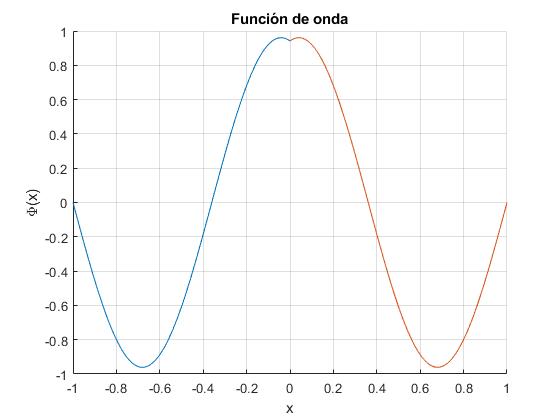
Estado n=1, simétricas, la energía es proporcional a 2.0288². Alterado en las proximidades del origen por la presencia del potencial delta de Dirac

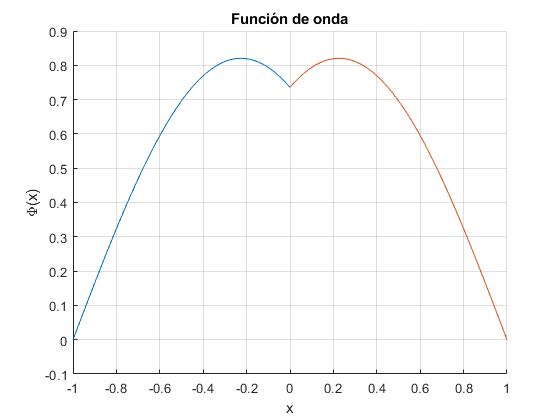
Estado n=2, antisimétricas, la energía es proporcional a 3.1416². No se ve alterado por la presencia del potencial delta, ya que la función de onda se anula en el origen

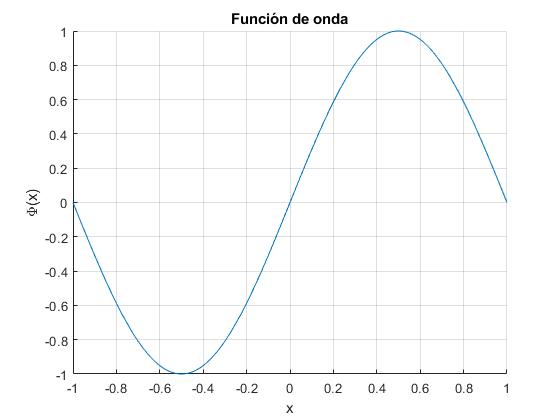
Estado n=3, simétricas, la energía es proporcional a 4.9132². Está muy poco alterado por la presencia del potencial delta, en comparación con el estado fundamental

Pozo de potencial delta de Dirac desplazado del origen

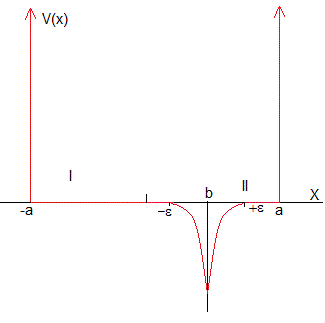
Consideremos ahora un pozo de potencial de altura infinita y anchura 2a, con pozo a de potencial delta de Dirac centrada en x=b.

Representamos el potencial delta de Dirac por la función que se muestra en la figura, un pozo de anchura 2ε y altura que tiende a infinito, siendo ε→0.

Vamos a resolver la ecuación de Schrödinger unidimensional en el potencial

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}\frac{d^2\psi (x)}{d{x}^2}+V(x)·\psi (x)=E·\psi (x)\\ V(x)\{\begin{array}{l}-a<x,\infty \\ -a<x<a,-\alpha \frac{{\hslash }^2}{2m}\delta (x-b)\\ x>a,\infty \end{array}\end{array}}$

La energía, E>0

• Región I

${\displaystyle \begin{array}{l}\frac{d^2\psi }{d{x}^2}+\frac{2m}{{\hslash }^2}E·\psi =\mathrm{0,}{k}^2=\frac{2m}{{\hslash }^2}E\\ {\psi }_I(x)=A\exp (-ikx)+B\exp (ikx),-a<x<b\end{array}}$

En x=-a el potencial es infinito

${\displaystyle \begin{array}{l}{\psi }_I(-a)=0\\ A\exp (ika)+B\exp (-ika)=0\end{array}}$

• Región II,

${\displaystyle \begin{array}{l}\frac{d^2\psi }{d{x}^2}+k^2·\psi =\mathrm{0,}{k}^2=\frac{2m}{{\hslash }^2}E\\ {\psi }_{II}(x)=C\exp (-ikx)+D\exp (ikx),b<x<a\end{array}}$

En x=a el potencial es infinito

${\displaystyle \begin{array}{l}{\psi }_{II}(a)=0\\ C\exp (-ika)+D\exp (ika)=0\end{array}}$

Niveles de energía

• La función de onda es continua en x=a

${\displaystyle \begin{array}{l}{\psi }_I(b)={\psi }_{II}(b)\\ A\exp (-ikb)+B\exp (ikb)=C\exp (-ikb)+D\exp (ikb)\end{array}}$

• La derivada primera de la función de onda NO es continua en x=a

Integramos la ecuación de Schrödinger en el pequeño intervalo b-ε, b+ε

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}{\displaystyle \underset{b-\epsilon }{\overset{b+\epsilon }{\int }}\frac{d^2\psi (x)}{d{x}^2}}dx-{\displaystyle \underset{b-\epsilon }{\overset{b+\epsilon }{\int }}\alpha \frac{{\hslash }^2}{2m}\delta (x)·\psi (x)·dx}=E·{\displaystyle \underset{b-\epsilon }{\overset{\epsilon +b}{\int }}\psi (x)·dx}\\ -\frac{{\hslash }^2}{2m}\underset{\epsilon \to 0}{\lim }\left({\frac{d{\psi }_{II}(x)}{dx}|}_{b+\epsilon }-{\frac{d{\psi }_I(x)}{dx}|}_{b-\epsilon }\right)-\alpha \frac{{\hslash }^2}{2m}{\psi }_I(b)=0\\ \underset{\epsilon \to 0}{\lim }\left({-ikC\exp (-ikx)+ikD\exp (ikx)|}_{b+\epsilon }{-\left(-ikA\exp (-ikx)+ikB\exp (ikx)\right)|}_{b-\epsilon }\right)+\alpha \left(A\exp (-ikb)+B\exp (ikb)\right)=0\\ \underset{\epsilon \to 0}{\lim }\left(\left(-ikC\exp \left(-ik(b+\epsilon )\right)+ikD\exp \left(ik(b+\epsilon )\right)\right)-\left(-ikA\exp \left(-ik(b-\epsilon )\right)+ikB\exp \left(ik(b-\epsilon )\right)\right)\right)+\alpha \left(A\exp (-ikb)+B\exp (ikb)\right)=0\\ \left(-ikC\exp \left(-ikb\right)+ikD\exp \left(ikb\right)\right)-\left(-ikA\exp \left(-ikb\right)+ikB\exp \left(ikb\right)\right)+\alpha \left(A\exp (-ikb)+B\exp (ikb)\right)=0\\ (\alpha +ik)A\exp \left(-ikb\right)+(\alpha -ik)B\exp \left(ikb\right)=ikC\exp \left(-ikb\right)-ikD\exp \left(ikb\right)\end{array}}$

Teniendo en cuenta la relación entre A y B y entre C y D, las dos ecuaciones se escriben

${\displaystyle \begin{array}{l}\{\begin{array}{l}(\alpha +ik)A\exp \left(-ikb\right)-(\alpha -ik)A\exp \left(ik(2a+b)\right)=ikC\exp \left(-ikb\right)+ikC\exp \left(ik(-2a+b)\right)\\ A\exp \left(-ikb\right)-A\exp \left(ik(2a+b)\right)=C\exp \left(-ikb\right)-C\exp \left(ik(-2a+b)\right)\end{array}\\ \frac{(\alpha +ik)\exp \left(-ikb\right)-(\alpha -ik)\exp \left(ik(2a+b)\right)}{\exp \left(-ikb\right)-\exp \left(ik(2a+b)\right)}=\frac{ik\exp \left(-ikb\right)+ik\exp \left(ik(-2a+b)\right)}{\exp \left(-ikb\right)-\exp \left(ik(-2a+b)\right)}\end{array}}$

El resultado después de simplificar esta expresión es

${\displaystyle \alpha \left(\cos (2kb)-\cos (2ka)\right)-2k\sin (2ka)=0}$

Caso particular: cuando b=0

${\displaystyle \begin{array}{l}\alpha {\sin }^2(ka)-2k\sin (ka)\cos (ka)=0\\ \sin (ka)\left(\alpha \sin (ka)-2k\cos (ka)\right)=0\end{array}}$

Un resultado similar hemos obtenido en el apartado anterior

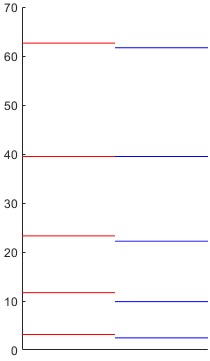
En la figura, se muestran en color azul, los niveles de energía de un pozo de potencial de altura infinita y de anchura 2a=2·1. Cuando se introduce en la posición b=0.5 un pozo de potencial delta de Dirac cuyo parámetro α=2, los niveles incrementan ligeramente la energía (en color rojo)

El código para representar los niveles es

function dirac
    a=1; %anchura del pozo 2a
    b=0.5; %Posición del potencial delta
    alfa=2; %parámetro
    f=@(k) alfa*(cos(2*k*a)-cos(2*k*b))-2*k.*sin(2*k*a);
    x=linspace(0,20,40);
    r1=raices(f,x); 
    disp(r1)
    for n=1:5
        E=(n*pi/(2*a))^2; %pozo de potencial de altura infinita
        line([1,2],[E,E], 'color','b')
        E=r1(n)^2; %pozo de potencial con delta de Dirac
        line([0,1],[E,E],'color','r')
    end
    xlabel('x')
    ylabel('E')
    title('Niveles de energía')
    
    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
    end
end

    1.7768    3.4204    4.8261    6.2832    7.9131    9.5291   11.0429   

Cuando b=0, obtenemos la misma figura del apartado anterior, con los mismas energías de los niveles

    2.0288    3.1416    4.9132    6.2832    7.9787    9.4248   11.0855 

Funciones de onda

${\displaystyle \begin{array}{l}{\psi }_I(x)=A\exp (-ikx)-A\exp (2ika)\exp (ikx),-a<x<b\\ {\psi }_{II}(x)=C\exp (-ikx)-C\exp (-2ika)\exp (ikx),b<x<a\end{array}}$

Los coeficientes A y C están relacionados, ya que la función de onda es continua en x=b

${\displaystyle \begin{array}{l}A\exp (-ikb)-A\exp (2ika)\exp (ikb)=C\exp (-ikb)-C\exp (-2ika)\exp (ikb)\\ C=A\frac{\exp (-ikb)-\exp (2ika)\exp (ikb)}{\exp (-ikb)-\exp (-2ika)\exp (ikb)}\\ {\left|C\right|}^2=A^2\frac{2-2\cos \left(2k(a-b)\right)-2\cos \left(2k(a+b)\right)+\cos (4ka)+\cos (4kb)}{2{\left(1-\cos \left(2k(a-b)\right)\right)}^2}\\ {\left|C\right|}^2=A^2\frac{{\left(\cos (2ka)-\cos (2kb)\right)}^2}{4{\sin }^4\left(k(a-b)\right)}\end{array}}$

El coeficiente A se determina de modo que

${\displaystyle \begin{array}{l}{\displaystyle \underset{-a}{\overset{b}{\int }}{\left|{\psi }_I(x)\right|}^{2}dx}+{\displaystyle \underset{b}{\overset{a}{\int }}{\left|{\psi }_{II}(x)\right|}^{2}dx}=1\\ A^2{\displaystyle \underset{-a}{\overset{b}{\int }}\left(2-e^{-2ika}{e}^{-2ikx}-e^{2ika}{e}^{2ikx}\right)dx+}{C}^2{\displaystyle \underset{-a}{\overset{b}{\int }}\left(2-e^{2ika}{e}^{-2ikx}-e^{-2ika}{e}^{2ikx}\right)dx=1}\\ A^2\left(2(a+b)-\frac{1}{k}\sin \left(2k(a+b)\right)\right)+C^2\left(2(a-b)-\frac{1}{k}\sin \left(2k(a-b)\right)\right)=1\end{array}}$

Representamos las funciones de onda correspondientes al primer nivel (estado fundamental), n=1, segundo, n=2, para un pozo de potencial de altura infinita y de anchura 2a=2·1, que contiene un pozo de potencial, delta de Dirac, de parámetro α=2, situado en b=0.5

function dirac_2
    a=1;   %anchura del pozo 2a
    b=0.5; %posición potencial delta
    alfa=2; %parámetro
    %niveles de energía
    f=@(k) alfa*(cos(2*k*a)-cos(2*k*b))-2*k.*sin(2*k*a);
    x=linspace(0,20,40);
    r1=raices(f,x); 
    
    %funciones de onda
    hold on
    n=2; %nivel (cambiar), 1,2,3,4...
    k=r1(n);
    if b==0 & rem(n,2)==0
        C=1;
        fplot(@(x) sin(k*x)/sqrt(a),[-a,a])
    else
        C=(cos(2*k*a)-cos(2*k*b))/(2*sin(k*(a-b))^2);   
        A=1/sqrt(2*(a+b)-sin(2*k*(a+b))/k+C^2*(2*(a-b)-sin(2*k*(a-b))/k));
        fplot(@(x) real(A*(exp(-1i*k*x)-exp(1i*k*(2*a+x)))),[-a,b])
        fplot(@(x) real(-A*C*(exp(-1i*k*x)-exp(1i*k*(-2*a+x)))),[b,a])
    end
    hold off
    grid on
    xlabel('x')
    ylabel('\Psi(x)')
    title('Función de onda')

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for m=1:length(indices)
            r(m)=fzero(f, [x(indices(m)), x(indices(m)+1)]);
        end
    end
end

Estado n=1, la energía es proporcional a 1.7768².

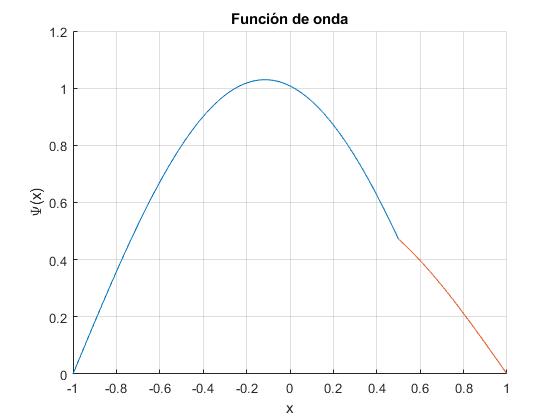
Estado n=2, la energía es proporcional a 3.4204².

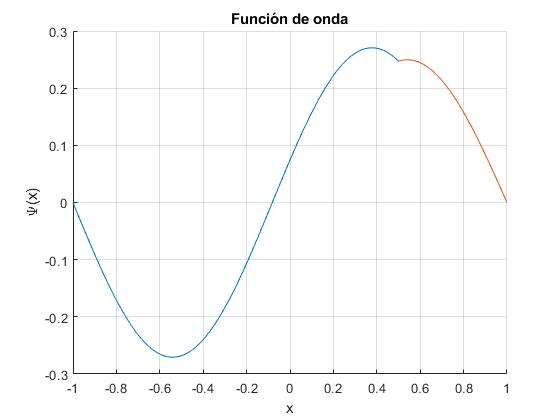
Cuando b=0, obtenemos las mismas figuras del apartado anterior

La energía, E<0

• Región I

${\displaystyle \begin{array}{l}\frac{d^2\psi }{d{x}^2}+\frac{2m}{{\hslash }^2}E·\psi =\mathrm{0,}{k}^2=-\frac{2m}{{\hslash }^2}E\\ {\psi }_I(x)=A\exp (-kx)+B\exp (kx),-a<x<b\end{array}}$

En x=-a el potencial es infinito

${\displaystyle \begin{array}{l}{\psi }_I(-a)=0\\ A\exp (ka)+B\exp (-ka)=0\end{array}}$

• Región II,

${\displaystyle \begin{array}{l}\frac{d^2\psi }{d{x}^2}+k^2·\psi =\mathrm{0,}{k}^2=-\frac{2m}{{\hslash }^2}E\\ {\psi }_{II}(x)=C\exp (-kx)+D\exp (kx),b<x<a\end{array}}$

En x=a el potencial es infinito

${\displaystyle \begin{array}{l}{\psi }_{II}(a)=0\\ C\exp (-ka)+D\exp (ka)=0\end{array}}$

Niveles de energía

• La función de onda es continua en x=a

${\displaystyle $ \begin{array}{l}{\psi }_I(b)={\psi }_{II}(b)\\ A\exp (-kb)+B\exp (kb)=C\exp (-kb)+D\exp (kb)\end{array}$}$

• La derivada primera de la función de onda NO es continua en x=a

Integramos la ecuación de Schrödinger en el pequeño intervalo b-ε, b+ε

${\displaystyle \begin{array}{l}-\frac{{\hslash }^2}{2m}{\displaystyle \underset{b-\epsilon }{\overset{b+\epsilon }{\int }}\frac{d^2\psi (x)}{d{x}^2}}dx-{\displaystyle \underset{b-\epsilon }{\overset{b+\epsilon }{\int }}\alpha \frac{{\hslash }^2}{2m}\delta (x)·\psi (x)·dx}=E·{\displaystyle \underset{b-\epsilon }{\overset{b+\epsilon }{\int }}\psi (x)·dx}\\ -\frac{{\hslash }^2}{2m}\underset{\epsilon \to 0}{\lim }\left({\frac{d{\psi }_{II}(x)}{dx}|}_{b+\epsilon }-{\frac{d{\psi }_I(x)}{dx}|}_{b-\epsilon }\right)-\alpha \frac{{\hslash }^2}{2m}{\psi }_{II}(b)=0\\ \underset{\epsilon \to 0}{\lim }\left({-kC\exp (-kx)+kD\exp (kx)|}_{b+\epsilon }{-\left(-kA\exp (-kx)+kB\exp (kx)\right)|}_{b-\epsilon }\right)+\alpha \left(C\exp (-kb)+D\exp (kb)\right)=0\\ \underset{\epsilon \to 0}{\lim }\left(\left(-kC\exp \left(k(b+\epsilon )\right)+kD\exp \left(k(b+\epsilon )\right)\right)-\left(-kA\exp \left(-k(b-\epsilon )\right)+kB\exp \left(k(b-\epsilon )\right)\right)\right)+\alpha \left(C\exp (-kb)+D\exp (kb)\right)=0\\ \left(-kC\exp \left(-kb\right)+kD\exp \left(kb\right)\right)-\left(-kA\exp \left(-kb\right)+kB\exp \left(kb\right)\right)+\alpha \left(C\exp (-kb)+D\exp (kb)\right)=0\end{array}}$

Teniendo en cuenta la relación entre A y B y entre C y D, las dos ecuaciones se escriben

${\displaystyle \begin{array}{l}\{\begin{array}{l}A\exp \left(-kb\right)-A\exp \left(k(2a+b)\right)=C\exp \left(-kb\right)-C\exp \left(k(-2a+b)\right)\\ kA\exp \left(-kb\right)+kA\exp \left(k(2a+b)\right)=(k-\alpha )C\exp \left(-kb\right)+(k+\alpha )C\exp \left(k(-2a+b)\right)\end{array}\\ \frac{\exp \left(-kb\right)-\exp \left(k(2a+b)\right)}{k\left(\exp \left(-kb\right)+\exp \left(k(2a+b)\right)\right)}=\frac{\exp \left(-kb\right)-\exp \left(k(-2a+b)\right)}{(k-\alpha )\exp \left(-kb\right)+(k+\alpha )\exp \left(k(-2a+b)\right)}\end{array}}$

El resultado después de simplificar esta expresión es

${\displaystyle \alpha \left(\cosh (2ka)-\cosh (2kb)\right)-2k\sinh (2ka)=0}$

Caso particular: cuando b=0

${\displaystyle \sinh (ka)\left(\alpha \sinh (ka)-2k\cosh (ka)\right)=0}$

La solución sinh(ka)=0, implica que k=0, y la energía E=0. La otra solución es

${\displaystyle \alpha \sinh (ka)-2k\cosh (ka)=0}$

Se calculan los niveles de energía de un pozo de potencial de altura infinita y de anchura 2a=2·2, cuando se introduce en la posición b=1 un pozo de potencial delta de Dirac cuyo parámetro α=2

function dirac_1
    a=2; %anchura del pozo 2a
    b=1; %posición potencial delta
    alfa=2;
    f=@(k) alfa*(cosh(2*k*a)-cosh(2*k*b))-2*k.*sinh(2*k*a);
    kk=linspace(0,5,10);
    kn=raices(f,kk);
    disp(kn)
 
    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for m=1:length(indices)
            r(m)=fzero(f, [x(indices(m)), x(indices(m)+1)]);
        end
    end
end

Obtenemos un único nivel cuya energía es proporcional a -0.7873²

    0.7873

Cuando b=0, obtenemos un único nivel de energía, k=0.9575, muy próximo al valor obtenido α/2=1 para un pozo de potencial delta de Dirac. Cuando mayor sea la anchura a del pozo más cerca estará del valor α/2=1. Se suguiere probar con a=5

Cuando a≤2/α no hay niveles. Se sugiere probar con a=1 y α=2

Función de onda

Los coeficientes A y C están relacionados, ya que la función de onda es continua en x=b

${\displaystyle \begin{array}{l}A\exp \left(-kb\right)-A\exp \left(k(2a+b)\right)=C\exp \left(-kb\right)-C\exp \left(k(-2a+b)\right)\\ C=A\frac{\exp (-kb)-\exp \left(k(-2a+b)\right)}{\exp (-kb)-\exp \left(k(2a+b)\right)}\end{array}}$

El coeficiente A se determina de modo que

${\displaystyle \begin{array}{l}{\displaystyle \underset{-a}{\overset{b}{\int }}{\left|{\psi }_I(x)\right|}^{2}dx}+{\displaystyle \underset{b}{\overset{a}{\int }}{\left|{\psi }_{II}(x)\right|}^{2}dx}=1\\ A^2{\displaystyle \underset{-a}{\overset{b}{\int }}\left(e^{-2kx}+e^{4ka}{e}^{2kx}-2e^{2ka}\right)dx+}{C}^2{\displaystyle \underset{-a}{\overset{b}{\int }}\left(e^{-2kx}+e^{-4ka}{e}^{2kx}-2e^{-2ka}\right)dx=1}\\ A^2\left(\frac{e^{-2kb}}{2k}-\frac{e^{2k(2a+b)}}{2k}-2e^{2ka}(a+b)\right)+C^2\left(\frac{e^{-2kb}}{2k}-\frac{e^{-2k(2a-b)}}{2k}-2e^{-2ka}(a-b)\right)=1\end{array}}$

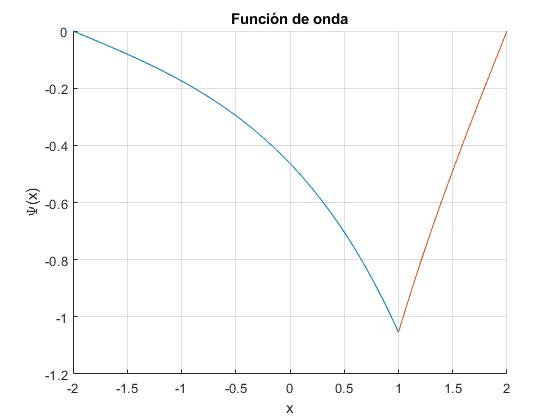
Añadimos al script el código que representa la función de onda correspondiente al único nivel de energía

function dirac_1
    a=2;
    b=1;
    alfa=2;
    f=@(k) alfa*(cosh(2*k*a)-cosh(2*k*b))-2*k.*sinh(2*k*a);
    kk=linspace(0,5,10);
    kn=raices(f,kk);
    disp(kn)
 
    k=kn(1);
    C=(exp(-k*b)-exp(k*(2*a+b)))/(exp(-k*b)-exp(k*(-2*a+b)));
    A=1/sqrt(-exp(-2*k*b)/(2*k)+exp(2*k*(2*a+b))/(2*k)-2*exp(2*k*a)*
(a+b)+C^2*(exp(-2*k*b)/(2*k)-exp(-2*k*(2*a-b))/(2*k)-2*exp(-2*k*a)*(a-b)));
    hold on
    fplot(@(x) A*(exp(-k*x)-exp(k*(2*a+x))),[-a,b])
    fplot(@(x) A*C*(exp(-k*x)-exp(k*(-2*a+x))),[b,a])
    hold off
    grid on
    xlabel('x')
    ylabel('\Psi(x)')
    title('Función de onda')

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for m=1:length(indices)
            r(m)=fzero(f, [x(indices(m)), x(indices(m)+1)]);
        end
    end
end

Referencias

I. Richard Lapidus. One-dimensional hydrogen atom in an infinite square well. Am J. Phys. 50 (6) June 1982, pp. 563-564

Armando Martínez Téllez. El potencial delta de Dirac