${\displaystyle E_p(x)=-D+D{\left(1-e^{-kx}\right)}^2}$

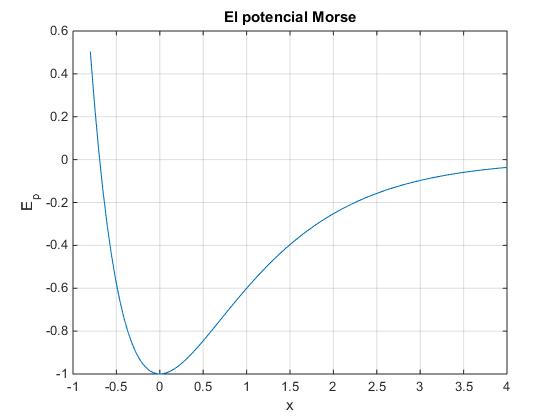
El potencial presenta un mínimo para x=0 cuyo valor es E_p(x₀)=-D.

Cuando x→∞, la función E_p(x) tiende a cero.

Cuando x→-∞, la función E_p(x) tiende a infinito.

En la figura, se muestra la gráfica de la función E_p(x) para k=1, y D=1

${\displaystyle E_p(x)=e^{-2x}-2e^{-x}}$

k=1;
D=1;
fplot(@(x) -D+D*(1-exp(-k*x)).^2, [-0.8,4])
grid on
xlabel('x')
ylabel('E_p');
title('El potencial de Morse')

Descripción cualitativa del movimiento de la partícula

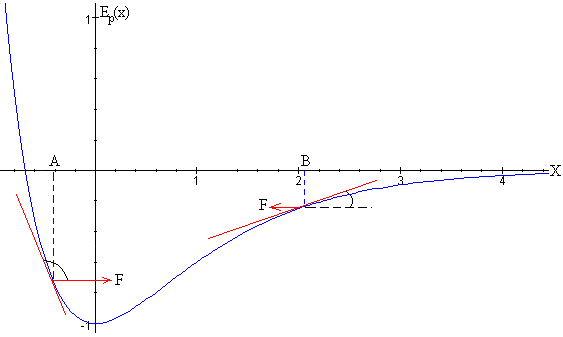
Dada la función E_p(x), la fuerza F(x) que actúa sobre la partícula es

${\displaystyle F(x)=-\frac{d{E}_p(x)}{dx}=-2Dk\left(1-e^{-kx}\right)e^{-kx}}$  

Para x=0, F(x)=0, el origen es una posición de equilibrio estable, ya que la energía potencial es mínima.

La fuerza sobre la partícula se obtiene midiendo la pendiente en cada punto de la función energía potencial E_p(x) cambiada de signo.

• Si la partícula está situada en la posición A, la pendiente es negativa, la fuerza es positiva, la pendiente es grande en módulo, la fuerza es grande.

• Si la partícula está situada en la posición B, la pendiente es positiva, la fuerza es negativa, la pendiente es pequeña, la fuerza es pequeña.

Como la fuerza que actúa sobre la partícula es conservativa, la energía total E permanece constante.

${\displaystyle \frac{1}{2}m{v}^2+E_p(x)=E}$

Dibujando función la energía potencial E_p(x), y conociendo el valor de la energía total E describimos de forma cualitativa el movimiento de la partícula.

1. Cuando la energía total E está en el intervalo -D<E<0, la partícula oscila entre dos posiciones x₁ y x₂ alrededor de la posición de equilibrio estable x=0.



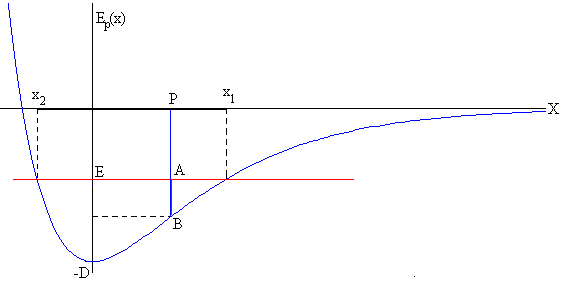
Estas dos posiciones son las raíces de la ecuación E_p(x) =E

${\displaystyle x=-\frac{1}{k}\ln \left(1\pm \sqrt{\frac{E+D}{D}}\right)}$

Si la partícula está situada en la posición P, la energía total es la medida del segmento PA, la energía potencial el segmento PB y la energía cinética el segmento AB.

La energía cinética es máxima cuando la partícula pasa por el origen y es nula cuando la partícula pasa por en las posiciones extremas x₁ y x₂.

2. Cuando E>0, la partícula se mueve desde el infinito, hasta una posición x_m y regresa de nuevo al infinito.



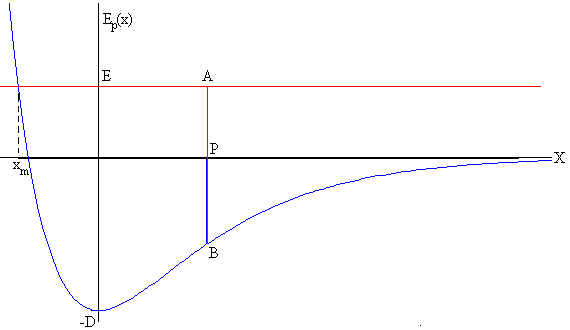
Cuando E>0, la ecuación E_p(x) =E solamente tiene una raíz

${\displaystyle x=-\frac{1}{k}\ln \left(1+\sqrt{\frac{E+D}{D}}\right)}$

Si la partícula está situada en la posición P, la energía total es la medida del segmento PA, la energía potencial el segmento PB y la energía cinética el segmento AB.

La energía cinética es máxima cuando la partícula pasa por el origen y es nula cuando la partícula está en la posición extrema x_m

Movimiento de la partícula

Si definimos el parámetro adimensional ρ tal que E+D=ρ·D

1. La partícula está confinada, si ρ<1 en la región

${\displaystyle -\frac{1}{k}\ln \left(1+\sqrt{\rho }\right)\le x\le -\frac{1}{k}\ln \left(1-\sqrt{\rho }\right)}$

2. La partícula se mueve hacia el infinito si ρ>1

${\displaystyle x\ge -\frac{1}{k}\ln \left(1+\sqrt{\rho }\right)}$

3. La partícula se mueve hacia el infinito si E=0 ó ρ=1

${\displaystyle x\ge -\frac{1}{k}\ln 2}$

Vamos a determinar la posición x de la partícula en función del tiempo t para cada uno de los casos, integrando una ecuación diferencial de primer orden. Escribimos el principio de conservación de la energía de la forma

${\displaystyle \begin{array}{l}\frac{1}{2}m{\left(\frac{dx}{dt}\right)}^2+D{\left(1-e^{-kx}\right)}^2=E+D\\ {\left(\frac{dx}{dt}\right)}^2=\left[\rho -{\left(1-e^{-kx}\right)}^2\right]\frac{2D}{m}\end{array}}$

1. Estudiamos el caso, ρ<1

Hacemos el cambio de variable

${\displaystyle e^{kx}=\frac{1-\sqrt{\rho }u}{1-\rho }\frac{dx}{dt}=\frac{-\sqrt{\rho }}{k(1-\sqrt{\rho }u)}\frac{du}{dt}}$

La ecuación diferencial de primer orden se transforma, haciendo algunas operaciones, en una ecuación diferencial fácilmente integrable

${\displaystyle \begin{array}{l}{\left(\frac{du}{dt}\right)}^2=\frac{2k^{2}D(1-\rho )}{m}(1-u^2)\\ {\displaystyle \int \frac{du}{\sqrt{1-u^2}}}=\gamma {\displaystyle \int dt}\gamma =\sqrt{\frac{2k^{2}D(1-\rho )}{m}}\end{array}}$

arccos u=γt-γt₀
u=cos(γt-γt₀)

γt₀ es la constante de integración que se determina a partir de las condiciones iniciales, la posición x₀ del móvil en el instante t=0.

Deshaciendo el cambio

${\displaystyle x=\frac{1}{k}\ln \left(\frac{1-\sqrt{\rho }\cos (\gamma t-\gamma t_0)}{1-\rho }\right)}$

En el programa interactivo, la posición inicial de la partícula t=0, es el origen x=0, el instante t₀ vale entonces,

${\displaystyle t_0=\frac{1}{\gamma }{\cos }^{-1}\left(\sqrt{\rho }\right)}$

Periodo

Dada la posición x en función del tiempo t, despejamos el tiempo t

${\displaystyle t=t_0+\frac{1}{\gamma }\arccos \left(\frac{1-\left(1-\rho \right)e^{kx}}{\sqrt{\rho }}\right)}$

La posición extrema x₁ la alcanza en el instante t₁

${\displaystyle \begin{array}{l}{x}_1=-\frac{1}{k}\ln \left(1+\sqrt{\rho }\right)\\ t_1=t_0+\frac{1}{\gamma }\arccos \left(\frac{1-\frac{1-\rho }{1+\sqrt{\rho }}}{\sqrt{\rho }}\right)=t_0+\frac{1}{\gamma }\arccos (1)=t_0\end{array}}$

La posición extrema x₂ la alcanza en el instante t₂

${\displaystyle \begin{array}{l}{x}_2=-\frac{1}{k}\ln \left(1-\sqrt{\rho }\right)\\ t_2=t_0+\frac{1}{\gamma }\arccos \left(\frac{1-\frac{1-\rho }{1-\sqrt{\rho }}}{\sqrt{\rho }}\right)=t_0+\frac{1}{\gamma }\arccos (-1)=t_0+\frac{\pi }{\gamma }\end{array}}$

El periodo es el doble de la diferencia de tiempos, 2(t₂-t₁)=2π/γ

2. Estudiamos el caso, ρ>1

Hacemos el cambio de variable

${\displaystyle e^{kx}=\frac{\sqrt{\rho }u-1}{\rho -1}\frac{dx}{dt}=\frac{\sqrt{\rho }}{k(\sqrt{\rho }u-1)}\frac{du}{dt}}$

La ecuación diferencial de primer orden se transforma, haciendo algunas operaciones, en una ecuación diferencial fácilmente integrable

${\displaystyle \begin{array}{l}{\left(\frac{du}{dt}\right)}^2=\frac{2k^{2}D(\rho -1)}{m}(u^2-1)\\ {\displaystyle \int \frac{du}{\sqrt{u^2-1}}}=\gamma {\displaystyle \int dt}\gamma =\sqrt{\frac{2k^{2}D(\rho -1)}{m}}\end{array}}$

arccosh u=γt-γt₀
u=cosh(γt-γt₀)

γt₀ es la constante de integración que se determina a partir de las condiciones iniciales, la posición x₀ del móvil en el instante t=0.

Deshaciendo el cambio

${\displaystyle x=\frac{1}{k}\ln \left(\frac{\sqrt{\rho }\cosh (\gamma t-\gamma t_0)-1}{\rho -1}\right)}$

En el programa interactivo, la posición inicial de la partícula t=0, es el origen x=0, el instante t₀ vale entonces

${\displaystyle t_0=\frac{1}{\gamma }{\cosh }^{-1}\left(\sqrt{\rho }\right)}$

3. En el caso límite ρ=1

Hacemos el cambio de variable

${\displaystyle e^{kx}=u\frac{dx}{dt}=\frac{1}{ku}\frac{du}{dt}}$

La ecuación diferencial de primer orden se transforma, haciendo algunas operaciones, en una ecuación diferencial fácilmente integrable

${\displaystyle \begin{array}{l}{\left(\frac{du}{dt}\right)}^2=\frac{2k^{2}D}{m}(2u-1)\\ {\displaystyle \int \frac{du}{\sqrt{2u-1}}}=\gamma {\displaystyle \int dt}\gamma =\sqrt{\frac{2k^{2}D}{m}}\end{array}}$

2u-1=(γt-γt₀)²

γt₀ es la constante de integración que se determina a partir de las condiciones iniciales, la posición x₀ del móvil en el instante t=0.

Deshaciendo el cambio

${\displaystyle x=\frac{1}{k}\ln \left(\frac{1+{(\gamma t-\gamma t_0)}^2}{2}\right)}$

En el programa interactivo, la posición inicial de la partícula t=0, es el origen x=0, el instante t₀ vale entonces,

${\displaystyle t_0=\frac{1}{\gamma }}$

Ejemplo:

• Valor del parámetro k=1

• Valor del parámetro D=1

1. Energía total de la partícula E=-0.5

El parámetro ρ=(E+D)/D=0.5<1

La partícula se mueve entre las posiciones extremas

${\displaystyle \begin{array}{l}{x}_1=-\frac{1}{k}\ln \left(1+\sqrt{\rho }\right)x_1=-\frac{1}{1}\ln \left(1+\sqrt{0.5}\right)=-0.53\\ x_2=-\frac{1}{k}\ln \left(1-\sqrt{\rho }\right)x_2=-\frac{1}{1}\ln \left(1-\sqrt{0.5}\right)=1.23\end{array}}$

La ecuación del movimiento es

${\displaystyle \begin{array}{l}x=\frac{1}{k}\ln \left(\frac{1-\sqrt{\rho }\cos (\gamma t-\gamma t_0)}{1-\rho }\right)\gamma =\sqrt{\frac{2k^{2}D(1-\rho )}{m}}{t}_0=\frac{1}{\gamma }{\cos }^{-1}\left(\sqrt{\rho }\right)\\ \gamma =\text{1}{t}_0=0.785\end{array}}$

En el instante t=2.0, la posición de la partícula es x=0.41.

La energía potencial es

${\displaystyle E_p(0.41)=-1+1·{\left(1-e^{-1·0.41}\right)}^2=\text{-0}\text{.887}}$

La energía cinética E_k=E-E_p=0.387

La velocidad de la partícula

${\displaystyle v=\sqrt{\frac{2E_k}{m}}=0.88}$

Representamos la posción x en función del tiempo t durante un periodo

k=1;
D=1;
E=-0.5; %energía de la partícula
m=1; %masa de la partícula

rho=(E+D)/D;
x1=-log(1+sqrt(rho))/k;
x2=-log(1-sqrt(rho))/k;
fprintf('Posiciones extremas [%1.3f, %1.3f]\n',x1,x2)
%ecuación del movimiento
gamma=sqrt(2*k^2*D*(1-rho)/m);
t0=acos(sqrt(rho))/gamma;
x=@(t) log((1-sqrt(rho)*cos(gamma*(t-t0)))/(1-rho))/k;
fplot(x, [0,2*pi/gamma]);
grid on
xlabel('t')
ylabel('x');
title('Posición en función del tiempo, E<0')



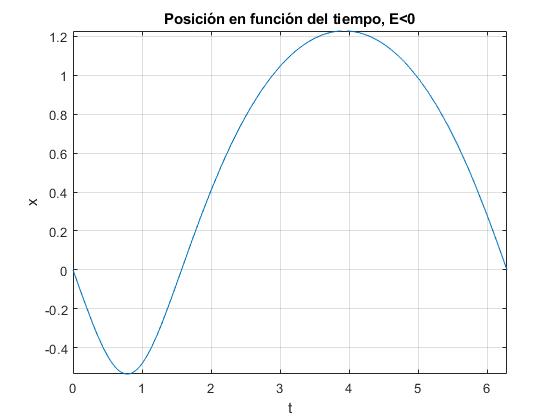
Posiciones extremas [-0.535, 1.228]

2. Energía total de la partícula E=0.5

El parámetro ρ=(E+D)/D=1.5>1

La partícula se mueve desde el origen hasta la posición x_m y luego, hasta el infinito

${\displaystyle x_m=-\frac{1}{k}\ln \left(1+\sqrt{\rho }\right)x_m=-\frac{1}{1}\ln \left(1+\sqrt{1.5}\right)=-0.80}$

La ecuación del movimiento es

${\displaystyle \begin{array}{l}x=\frac{1}{k}\ln \left(\frac{\sqrt{\rho }\cosh (\gamma t-\gamma t_0)-1}{\rho -1}\right)\gamma =\sqrt{\frac{2k^{2}D(\rho -1)}{m}}{t}_0=\frac{1}{\gamma }{\cosh }^{-1}\left(\sqrt{\rho }\right)\\ \gamma =\text{1}{t}_0=0.658\end{array}}$

En el instante t=2.0, la posición de la partícula es x=1.10

La energía potencial es

${\displaystyle E_p(1.10)=-1+1·{\left(1-e^{-1·1.10}\right)}^2=\text{-0}\text{.55}}$

La energía cinética E_k=E-E_p=1.05

La velocidad de la partícula v=1.45

k=1;
D=1;
m=1; %masa de la partícula
E=0.5; %energía de la partícula
rho=(E+D)/D;
x1=-log(1+sqrt(rho))/k;
fprintf('Posición extrema %1.3f\n',x1)
%ecuación del movimiento
gamma=sqrt(2*k^2*D*(rho-1)/m);
t0=acosh(sqrt(rho))/gamma;
x=@(t) log((sqrt(rho)*cosh(gamma*t-gamma*t0)-1)/(rho-1))/k;
fplot(x,[0,5]);
grid on
xlabel('t')
ylabel('x');
title('Posición en función del tiempo, E>0')



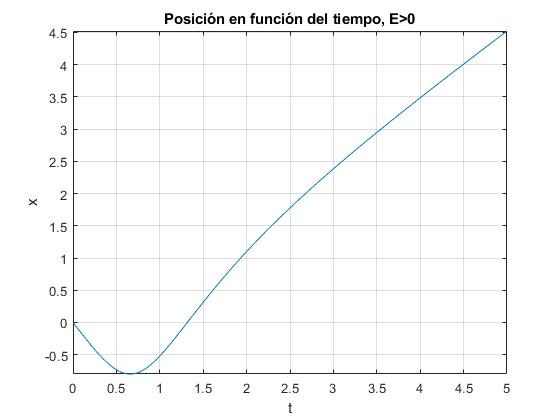
Posición extrema -0.800

3. Energía total de la partícula E=0

El parámetro ρ=(E+D)/D=1

La partícula se mueve desde el origen hasta la posición x_m y luego, hasta el infinito

${\displaystyle x_m=-\frac{1}{k}\ln 2=-0.69}$

La ecuación del movimiento es

${\displaystyle \begin{array}{l}x=\frac{1}{k}\ln \left(\frac{{(\gamma t-\gamma t_0)}^2+1}{2}\right)\gamma =\sqrt{\frac{2k^{2}D}{m}}{t}_0=\frac{1}{\gamma }\\ \gamma =\sqrt{2}{t}_0=\sqrt{2}/2\end{array}}$

En el instante t=2.0, la posición de la partícula es x=0.77

La energía potencial es

${\displaystyle E_p(0.77)=-1+1·{\left(1-e^{-1·0.77}\right)}^2=\text{-0}\text{.71}}$

La energía cinética E_k=E-E_p=0.71

La velocidad de la partícula v=1.19

k=1;
D=1;
E=0; %energía de la partícula
m=1; %masa de la partícula
rho=(E+D)/D;
x1=-log(2)/k;
fprintf('Posición extrema %1.3f\n',x1)
%ecuación del movimiento
gamma=sqrt(2*k^2*D/m);
t0=1/gamma;
x=@(t) log(((gamma*t-gamma*t0).^2+1)/2)/k;
fplot(x,[0,5]);
grid on
xlabel('t')
ylabel('x');
title('Posición en función del tiempo, E=0')



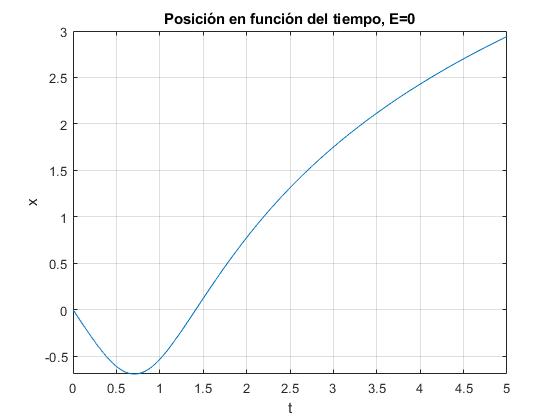
Posición extrema -0.693

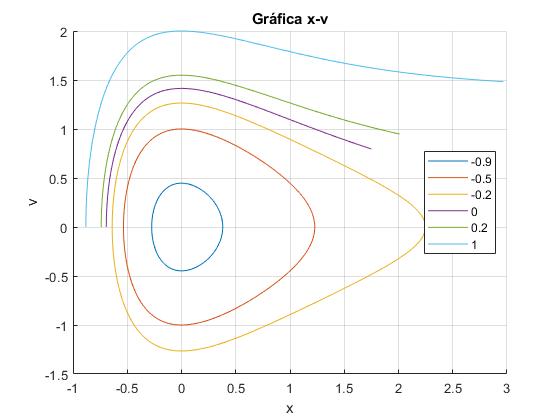
Representamos en el espacio de las fases (x-v) el movimiento de la partícula para varios valores de la energía. La partícula parte del origen x=0 en el instante t=0

k=1;
D=1;
m=1; %masa de la partícula
hold on
for E=-[0.9,0.5,0.2]  %energía <0
    rho=(E+D)/D;
    gamma=sqrt(2*k^2*D*(1-rho)/m);
    t0=acos(sqrt(rho))/gamma;
    x=@(t) log((1-sqrt(rho)*cos(gamma*t-gamma*t0))/(1-rho))/k;
    v=@(t) sqrt(rho)*gamma*sin(gamma*(t-t0))./(k*(1-sqrt(rho)*cos(gamma*(t-t0))));
   fplot(x,v,[0,2*pi/gamma],'displayName',num2str(E))
end

E=0;
gamma=sqrt(2*k^2*D/m);
t0=1/gamma;
x=@(t) log((1+(t-t0).^2*gamma^2)/2)/k;
v=@(t) 2*gamma^2*(t-t0)./(1+(t-t0).^2*gamma^2);
fplot(x,v,[t0,3],'displayName',num2str(E))

for E=[0.2,1] %energía >0
    rho=(E+D)/D;
    gamma=sqrt(2*k^2*D*(rho-1)/m);
    t0=acosh(sqrt(rho))/gamma;
    x=@(t) log((sqrt(rho)*cosh(gamma*t-gamma*t0)-1)/(rho-1))/k;
    v=@(t) sqrt(rho)*gamma*sinh(gamma*(t-t0))./(k*(sqrt(rho)*cosh(gamma*(t-t0))-1));
    fplot(x,v,[t0,3],'displayName',num2str(E))
end
hold off
legend('-DynamicLegend','location','east')
grid on
xlabel('x')
ylabel('v');
title('Gráfica x-v')

Actividades

Se introduce

• El parámetro k de la función energía potencial E_p(x), en el control titulado Parámetro.

• El parámetro D se ha fijado en el valor 1

• La energía total E de la partícula, en el control titulado Energía.

Se pulsa el botón titulado Nuevo.

Si la energía E de la partícula está en el intervalo -1<E<0, la partícula oscila entre dos posiciones x₁ y x₂.

Si la energía E de la partícula es positiva o nula, la partícula se mueve desde el origen hasta la posición extrema x_m y desde esta posición hacia el infinito.

Se indica mediante un segmento de color azul, el valor de la energía potencial, mediante un segmento de color rojo el valor de la energía cinética, y mediante una flecha la fuerza sobre la partícula.

En la parte superior, se proporcionan valores numéricos del tiempo t, la posición x, módulo de la velocidad v, energía potencial E_p, energía cinética E_k.

Referencias

DeMarcus W. C. Classical motion of a Morse oscillator. Am. J. Phys. 46 (7) July 1978, pp. 733-734