Un cohete de dos fases

Reparto óptimo de combustible entre las dos fases

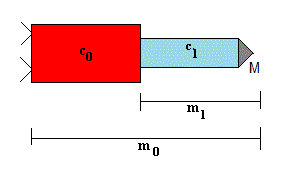
La masa inicial m₀ es la suma de la carga útil, más el combustible y más la masa de los recipientes que contienen el combustible. Para calcular esta última cantidad, se ha supuesto que los recipientes metálicos tiene una masa que es el factor r multiplicado por la masa de combustible. Donde r es del orden del 5% ó 0.05.

masa inicial, m₀=carga útil+(1+r) · combustible total.

m₀=M+(1+r)c

La cantidad de combustible en la primera fase c₀ es igual al producto del combustible total, por el tanto por ciento p y dividido por cien.

combustible en la primera fase c₀ =combustible total · tanto por ciento/100;

c₀=p·c

Una vez que ha transcurrido un tiempo t₀ igual al cociente entre el combustible en la primera fase c₀ y la cantidad D que se quema por segundo, t₀=c₀/D se alcanza una velocidad máxima v₀

$v_{0} = u \ln (\frac{m_{0}}{m_{0} - c_{0}}) = u \ln (\frac{M + (1 + r) c}{M + (1 + r - p) c})$

El cohete se desprende de la primera fase disminuyendo la masa inicial del cohete m₀ en una cantidad igual a la suma de la masa del combustible quemado c₀ y la masa del recipiente que lo contiene

masa inicial al encenderse la segunda fase, m₁=carga útil+(1+r) · c₁

m₁=M+(1+r)c₁

Siendo c₁ la masa de combustible de la segunda fase, que es igual a la masa del combustible total menos la masa de combustible de la primera fase c₀ ya quemado.

combustible en la segunda fase c₁ =combustible total - combustible en la primera fase c₀

c₁=(1-p)c

En el instante t₁ se agota el combustible de la segunda fase, es igual al cociente entre la masa de combustible total y la cantidad D que se quema por segundo

t₁=combustible total/D.

Cuando se agota el combustible, el cohete alcanza la velocidad máxima v₁, continuando con la misma velocidad ya que no actúan fuerzas sobre el mismo.

$v_{1} = v_{0} + u \ln (\frac{m_{1}}{m_{1} - c_{1}}) = u \ln (\frac{m_{0}}{m_{0} - c_{0}}) + u \ln (\frac{m_{1}}{m_{1} - c_{1}})$

Teniendo en cuenta que

$\begin{array}{l} m_{0} = M + (1 + r) c \\ m_{1} = M + (1 + r) c_{1} = M + (1 + r) (1 - p) c \\ m_{0} - c_{0} = M + (1 + r - p) c \\ m_{1} - c_{1} = M + r (1 - p) c \end{array}$

La velocidad final v₁ es una función de p

$\begin{array}{l} v_{1} = u \ln (\frac{m_{0}}{m_{0} - c_{0}} \frac{m_{1}}{m_{1} - c_{1}}) = u \ln (\frac{M + (1 + r) c}{M + (1 + r - p) c} \frac{M + (1 + r) (1 - p) c}{M + r (1 - p) c}) \\ v_{1} = u \ln (\frac{m + (1 + r)}{m + (1 + r - p)} \frac{m + (1 + r) (1 - p)}{m + r (1 - p)}), m = \frac{M}{c} \end{array}$

Para calcular el valor máximo de la velocidad v₁, derivamos con respecto de p. De este modo determinamos la proporción óptima de combustible en las dos fases p·c en la primera y (1-p)c en la segunda

Ya que m₀ no depende de p calculamos el extremo de la función

$f (p) = \frac{m + (1 + r) (1 - p)}{(m + 1 + r - p) (m + r (1 - p))}$

Obtenemos una ecuación de segundo grado en p

$\begin{array}{l} \frac{d f (p)}{d p} = \frac{- (1 + r) (m + 1 + r - p) (m + r (1 - p)) - {- (m + r (1 - p)) - r (m + 1 + r - p)} (m + (1 + r) (1 - p))}{{(m + 1 + r - p)}^{2} {(m + r (1 - p))}^{2}} = 0 \\ - (1 + r) (m + 1 + r - p) (m + r (1 - p)) + (m (1 + r) + r (2 + r - 2 p)) (m + (1 + r) (1 - p)) = 0 \\ - (1 + r) {m^{2} + m (1 + 2 r - p - r p) + r (1 + r - p) (1 - p)} + m^{2} (1 + r) + m {{(1 + r)}^{2} (1 - p) + r (2 + r - 2 p)} + r (2 + r - 2 p) (1 + r) (1 - p) = 0 \\ m {(1 + 4 r + 2 r^{2} - p - 4 p r - r^{2} p) - (1 + 2 r - p - r p) (1 + r)} + r (1 + r) (1 - p) {2 + r - 2 p - (1 + r - p)} = 0 \\ m r (1 - 2 p) + (1 + r) (1 - 2 p + p^{2}) r = 0 \\ p^{2} - 2 p (1 + \frac{m}{1 + r}) + (1 + \frac{m}{1 + r}) = 0 \end{array}$

La solución es la raíz p<1

$p = k - \sqrt{k^{2} - k}, k = 1 + \frac{m}{1 + r}$

u=2000; %velocidad de escape de los gases (respecto al cohete)
c=9000; %combustible
M=800;  %carga útil
r=0.05;
m=M/c;
%velocidad final del cohete
vf=@(p) u*log((m+(1+r))./(m+(1+r-p)))+u*log((m+(1+r)*(1-p))./(m+r*(1-p)));
fplot(vf,[0,1])
k=1+m/(1+r);
p_m=k-sqrt(k^2-k); %máximo
v_m=vf(p_m); %máxima velocidad
line([p_m,p_m],[4200,v_m],'lineStyle','--')
line([0,p_m],[v_m,v_m],'lineStyle','--')
disp(p_m) 
disp(vf(p_m)) %velocidad máxima
grid on
ylim([4200,4650])
xlabel('p');
ylabel('v_f(m/s)')
title('Proporción de combustible en la primera fase')

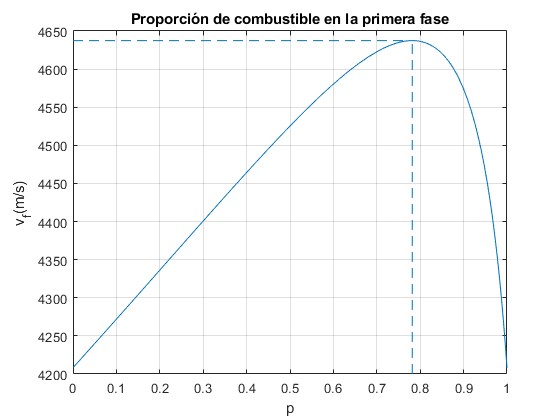
La proporción óptima es p=0.78 (78%) de combustible en la primera fase y 0.22 (22%) en la segunda. La velocidad máxima del cohete es 4 637 m/s

v_m =   4.6374e+03
>> p_m
p_m =    0.7816

Posición y velocidad del cohete en función del tiempo

Velocidad y posición del cohete en la primera etapa

Masa inicial del cohete, m₀=M+(1+r)·c.

Donde M es la carga útil y c es el combustible total

El combustible en la primera fase c₀=c·p

La velocidad y posición del cohete en el instante t

$\begin{array}{l} v = u \ln \frac{m_{0}}{m_{0} - D t} \\ x = u t \ln m_{0} + \frac{u}{D} ((m_{0} - D t) \ln (m_{0} - D t) + D t - m_{0} \ln m_{0}) \end{array}$

El combustible de la primera fase se agota en el instante t₀=c₀/D, en ese momento la posición x₀ y velocidad v₀ del cohete en este instante son, respectivamente

$\begin{array}{l} v_{0} = u \ln \frac{m_{0}}{m_{0} - c_{0}} \\ x_{0} = u \frac{c_{0}}{D} \ln m_{0} + \frac{u}{D} ((m_{0} - c_{0}) \ln (m_{0} - c_{0}) + c_{0} - m_{0} \ln m_{0}) \end{array}$

Velocidad y posición del cohete en la segunda etapa

Agotado el combustible de la primera fase queda c₁=c-c₀. La masa inicial del cohete es ahora m₁=M+(1+r)·c₁

La velocidad y posición del cohete en el instante t>t₀ es

$\begin{array}{l} v = v_{0} + u \ln \frac{m_{1}}{m_{1} - D (t - t_{0})} \\ x = x_{0} + v_{0} (t - t_{0}) + u (t - t_{0}) \ln m_{1} + \frac{u}{D} ((m_{1} - D (t - t_{0})) \ln (m_{1} - D (t - t_{0})) + D (t - t_{0}) - m_{1} \ln m_{1}) \end{array}$

El combustible se agota en el instante t=t₀+c₁/D=c/D

La velocidad final y la posición del cohete son, respectivamente

$\begin{array}{l} v_{1} = v_{0} + u \ln \frac{m_{1}}{m_{1} - c_{1}} \\ x_{1} = x_{0} + v_{0} \frac{c_{1}}{D} + u \frac{c_{1}}{D} \ln m_{1} + \frac{u}{D} ((m_{1} - c_{1}) \ln (m_{1} - c_{1}) + c_{1} - m_{1} \ln m_{1}) \end{array}$

Ejemplo

Combustible total en el cohete c=9000 kg
Carga útil que transporta M=800 kg
Combustible quemado por segundo D=1000 kg/s
Tanto por ciento de combustible en la primera fase, 70%, p=0.7
La velocidad constante de salida de los gases es u=2000 m/s respecto del cohete
La masa del recipiente que contiene el combustible es el 5%, r=0.05 de la masa del combustible

Primera fase

Masa total y combustible

m₀=800+9000+0.05·9000=10250 kg,
c₀=0.7·9000=5600 kg

Velocidad final y la posición del cohete al agotarse el combustible en la primera fase son, respectivamente.

$\begin{array}{l} v_{0} = 2000 \ln \frac{10250}{10250 - 5600} = 1907 m/s \\ x_{0} = 2000 \frac{5600}{1000} \ln 10250 + \frac{2000}{1000} ((10250 - 5600) \ln (10250 - 5600) + 5600 - 10250 \ln 10250) = 5067 m \end{array}$

Segunda fase

Estas son la velocidad inicial y la posición inicial para la segunda fase.

El combustible en la segunda fase es c₁=c-c₀=9000-5600=3400 kg
La masa inicial del cohete en esta fase es m₁=800+3400+0.05·3400=4370 kg

El tiempo que tarda en agotarse el combustible es c₁/D=3.4 s. La velocidad y posición final del cohete en el instante t=5.6+3.4=9 s es

$\begin{array}{l} v = v_{0} + 2000 \ln \frac{4370}{4370 - 3400} = 4623 m/s \\ x = x_{0} + v_{0} \cdot 3.4 + 2000 \cdot 3.4 \ln 4370 + \frac{2000}{1000} ((4370 - 3400) \ln (4370 - 3400) + 3400 - 4370 \ln 4370) = 13077 m \end{array}$

u=2000; %velocidad de escape de los gases (respecto al cohete)
combustible=9000; %combustible
c0=0.7*combustible;  %combustible en la primera fase
c1=combustible-c0; %combustible en la segunda fase
carga=800;  %carga útil
m0=carga+1.05*combustible; %masa inicial de la primara fase
m1=carga+1.05*c1; %masa inicial cuando empieza la segunda fase
D=1000; %kg de combustible quemado por segundo
t0=c0/D; %tiempo que tarda en agotarse el combustible de la primera fase
t1=c1/D; %tiempo que tarda en agotarse el combustible de la segunda fase
v0=u*log(m0/(m0-D*t0)); %velocidad final en la primera fase
%posición final primera fase
x0=u*t0*log(m0)+u*((m0-D*t0).*log(m0-D*t0)+D*t0-m0*log(m0))/D; 
v1=v0+u*log(m1/(m1-D*t1)); %velocidad final
%posición final
x1=x0+v0*t1+u*t1*log(m1)+u*((m1-D*t1).*log(m1-D*t1)+D*t1-m1*log(m1))/D; 
fprintf('Velocidad final %4.1f, posición final %5.1f en la 
primera fase\n',v0,x0);
fprintf('Velocidad final %4.1f, posición final %5.1f en la 
segunda fase\n',v1,x1);
 
figure
hold on
t=0:0.05:t0;
v=u*log(m0./(m0-D*t));
plot(t,v,'b');
t=0:0.05:t1;
v=v0+u*log(m1./(m1-D*t));
plot(t0,v(1),'ro','markersize',4,'markerfacecolor','r')
plot(t+t0,v,'r')
hold off
grid on
xlabel('t(s)')
ylabel('v(m/s)')
title('Velocidad')
 
figure
hold on
t=0:0.05:t0;
x=u*t*log(m0)+u*((m0-D*t).*log(m0-D*t)+D*t-m0*log(m0))/D;
plot(t,x,'b')
t=0:0.05:t1;
x=x0+v0*t+u*t*log(m1)+u*((m1-D*t).*log(m1-D*t)+D*t-m1*log(m1))/D;
plot(t0,x(1),'ro','markersize',4,'markerfacecolor','r')
plot(t+t0,x,'r')
hold off
grid on
xlabel('t(s)')
ylabel('x(m)')
title('Posición')

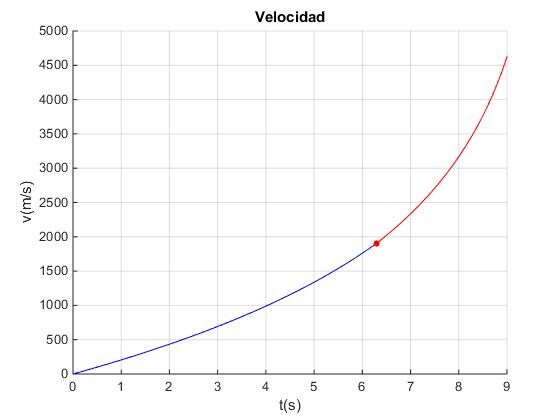
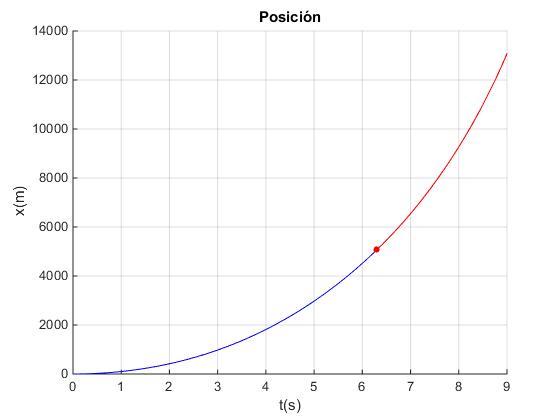
Velocidad final 1907.1, posición final 5066.9 en la primera fase
Velocidad final 4622.8, posición final 13077.0 en la segunda fase

Actividades

Se introduce

El combustible total en ambas fases, en el control titulado Combustible total en el cohete
El tanto por ciento del combustible total en la primera fase, en el control titulado Tanto por ciento de combustible en la primera fase
La carga útil que transporta el cohete, en el control titulado Carga útil que transporta
La cantidad D de combustible que se quema por segundo, en el control titulado Combustible quemado por seg.

Se pulsa el botón titulado Nuevo y a continuación, Empieza

Ahora se tratará de comprobar, que un cohete de dos fases que transporta la misma cantidad de combustible y la misma carga útil, es más ventajoso que el mismo cohete de una sola fase.

En segundo lugar, se tratará de investigar la dependencia de la velocidad final del cohete con el reparto de combustible total entre las dos fases. Manteniendo fijas la cantidad total de combustible y la carga útil, se tratará de modificar el tanto por ciento de combustible en la primera fase y anotar la velocidad final una vez agotado todo el combustible de la segunda fase. Comprobar la distribución óptima de combustible, aquella que da lugar a una mayor velocidad final, completando una tabla como la siguiente.

Tanto por ciento	Velocidad al desprenderse la primera fase	Velocidad final al agotarse el combustible de la segunda fase
10
20
30
40
50
60
70
80
90

Combustible total en el cohete (kg)<20000
Tanto por ciento de combustible en la primera fase
Combustible quemado por seg (kg/s) <2000
Carga útil <2000

Cohete de tres etapas

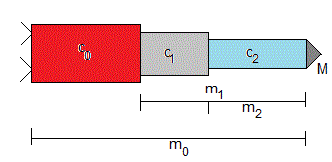
Sea un cohete de tres etapas. La cantidad de combustible de la primera etapa es, c₀=p₀c, de la segunda, c₁=p₁c y de la tercera, c₂=p₂c. Donde c es la cantidad total de combustible y p_i es la proporción de combustible en cada etapa, naturalmente, p₀+p₁+p₂=1

Vamos a determinar el reparto óptimo de combustible en cada una de las tres etapas

La velocidad final es

$v_{f} = u \ln (\frac{m_{0}}{m_{0} - c_{0}}) + u \ln (\frac{m_{1}}{m_{1} - c_{1}}) + u \ln (\frac{m_{2}}{m_{2} - c_{2}})$

Teniendo en cuenta que

$\begin{array}{l} m_{0} = M + (1 + r) c \\ m_{1} = M + (1 + r) (c_{1} + c_{2}) = M + (1 + r) (p_{1} + p_{2}) c \\ m_{2} = M + (1 + r) c_{2} = M + (1 + r) p_{2} c \\ m_{0} - c_{0} = M + (1 + r - p_{0}) c = M + (r + p_{1} + p_{2}) c \\ m_{1} - c_{1} = M + (1 + r) p_{2} c + r p_{1} c \\ m_{2} - c_{2} = M + r p_{2} c \end{array}$

La velocidad final, v_f, cuando se ha agotado el combustible, es

$\begin{array}{l} v_{f} = u \ln (\frac{m_{0}}{m_{0} - c_{0}} \frac{m_{1}}{m_{1} - c_{1}} \frac{m_{2}}{m_{2} - c_{2}}) = u \ln (\frac{M + (1 + r) c}{M + (r + p_{1} + p_{2}) c} \frac{M + (1 + r) (p_{1} + p_{2}) c}{M + (1 + r) p_{2} c + r p_{1} c} \frac{M + (1 + r) p_{2} c}{M + r p_{2} c}) = \\ u \ln (\frac{m + 1 + r}{m + r + p_{1} + p_{2}} \frac{m + (1 + r) (p_{1} + p_{2})}{m + (1 + r) p_{2} + r p_{1}} \frac{m + (1 + r) p_{2}}{m + r p_{2}}), m = \frac{M}{c} \end{array}$

Ya que m₀ no depende de p_i calculamos el extremo de la función

$f (p_{1}, p_{2}) = \frac{(m + (1 + r) (p_{1} + p_{2})) (m + (1 + r) p_{2})}{(m + r + p_{1} + p_{2}) (m + (1 + r) p_{2} + r p_{1}) (m + r p_{2})}$

Se trata de una función de dos variables p₁ que denominamos x y p₂ que denominamos y

$f (x, y) = \frac{(m + (1 + r) (x + y)) (m + (1 + r) y)}{(m + r + x + y) (m + (1 + r) y + r x) (m + r y)}$

El extremo dela función f(x,y) se calcula

$\frac{\partial f (x, y)}{\partial x} = 0, \frac{\partial f (x, y)}{\partial y} = 0$

Math Symbolic de MATLAB nos ayuda a calcular estas derivadas parciales y a resolver mediante el comando solve el sistema no lineal de dos ecuaciones con dos incógnitas x e y

syms m r x y;
z=(m+(1+r)*(x+y))*(m+(1+r)*y)/((m+r+x+y)*(m+(1+r)*y+r*x)*(m+r*y));
z_x=diff(z,x);
z_x=simplify(z_x);
z_y=diff(z,y);
z_y=simplify(z_y);

c=9000; %combustible
M=800;  %carga útil
z_x=subs(z_x,{m,r},{M/c,0.05});
z_y=subs(z_y,{m,r},{M/c,0.05});
eqns=[z_x==0, z_y==0];
s=solve(eqns,[x,y]);
disp(double(s.x))
disp(double(s.y))

   0.2654 + 0.0000i
  -0.1327 + 0.5730i
  -0.1327 - 0.5730i

   0.1134 + 0.0000i
  -0.1837 - 0.1716i
  -0.1837 + 0.1716i

La primera raíz real es el valor de x_m=p₁=0.2654
La segunda raíz real es el valor de y_m=p₂=0.1134
Naturalmente, p₀=1-p₁-p₂=0.6212

El reparto óptimo de combustible para este cohete de tres etapas es, 62.1% en la primera etapa, 26.5% en la segunda y 11.3% en la tercera

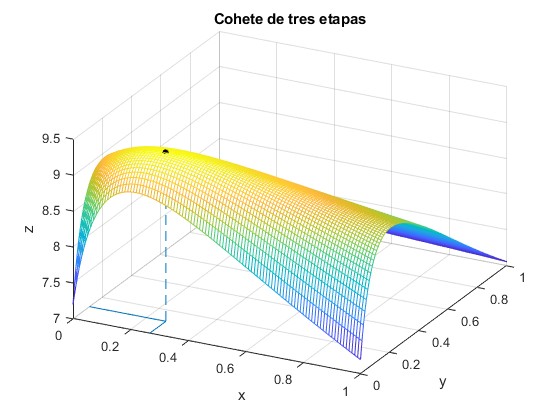
Vamos a comprobarlo representando la superficie f(x,y) y el valor de su extremo, z_m=f(x_m,y_m)

c=9000; %combustible
M=800;  %carga útil
r=0.05;
m=M/c;
%velocidad final del cohete
f=@(x,y) (m+(1+r)*(x+y)).*(m+(1+r)*y)./((m+(r+x+y)).*(m+(1+r)*y+r*x).*(m+r*y));
x=0:0.01:1;
y=0:0.01:1;
[X,Y]=meshgrid(x,y);
hold on
mesh(X,Y,f(X,Y));
x_m=0.2654;
y_m=0.1134;
z_m=f(x_m,y_m);
plot3(x_m, y_m, z_m,'ko','markersize',4,'markeredgecolor','k',
'markerfacecolor','k')
line([x_m,x_m], [y_m,y_m], [7,z_m],'lineStyle','--' )
line([0,x_m], [y_m,y_m], [7,7] )
line([x_m,x_m], [0,y_m], [7,7])
hold off
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('Cohete de tres etapas')
view(27,34)

Calculamos la velocidad (máxima posible) del cohete de tres etapas, para las proporciones óptimas

u=2000; %velocidad de escape de los gases (respecto al cohete)
c=9000; %combustible
M=800;  %carga útil
r=0.05;
m=M/c;
%velocidad final del cohete
p1=0.2654; %proporciones óptimas
p2=0.1134;
vm=u*log((m+1+r)*(m+(1+r)*(p1+p2))*(m+(1+r)*p2)/((m+r+p1+p2)*(m+(1+r)*p2+r*p1)
*(m+r*p2)));
disp(vm)

   4.7297e+03

Obtenemos con tres etapas una velocidad de 4 730 m/s un poco mayor que con dos etapas 4 637 m/s

Referencias

Díaz-Jiménez, A., Mathieu Valderrama R.. Redistribuyendo la masa con la velocidad: El cohete clásico. Revista Española de Física. Volumen 4, n° 3, 1990. págs. 65-67.