Movimiento vertical de un cohete

En la página titulada Un cohete de empuje constante, formulamos la ecuación del movimiento de un cohete que se mueve en el espacio exterior.

Consideremos un cohete que en el instante t, tiene una masa m que lleva una velocidad v respecto a un Sistema de Referencia Inercial (por ejemplo, la Tierra).

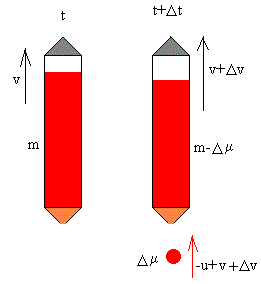
En el instante t+Δt, una masa Δμ de combustible se expulsa con una velocidad constante –u relativa al cohete, como consecuencia la velocidad de la masa restante (m-Δμ) del cohete se incrementa en v+Δv.

En el instante t, el cohete de masa m lleva una velocidad v. El momento lineal es

p(t)=mv

En el instante t+Δt

El cohete tiene una masa m-Δμ, su velocidad es v+Δv.
La masa expulsada Δμ lleva una velocidad –u respecto del cohete o una velocidad –u+v+Δv, respecto de Tierra

El momento lineal en este instante es

p(t+Δt)=(m-Δμ)(v+Δv)+ Δμ(–u+v+Δv)

El cambio de momento lineal entre los instantes t y t+Δt es

Δp=p(t+Δt)- p(t)=m·Δv-u·Δμ

En el límite cuando Δt→0

$\frac{d p}{d t} = m \frac{d v}{d t} - u \frac{d μ}{d t}$

El cambio de momento lineal se debe a la acción de las fuerzas exteriores al sistema (la fuerza de atracción gravitatoria, que apunta en sentido contrario al momento lineal).

$\frac{d p}{d t} = - m g$

Por otra parte, la masa M del sistema formado por el cohete m y el combustible expulsado μ es constante M=μ+m, por lo que dμ+dm=0. La masa del cohete disminuye en dm y aumenta la masa del combustible expulsado en la misma cantidad.

La ecuación del movimiento del cohete se escribe

$- m g = m \frac{d v}{d t} + u \frac{d m}{d t}$

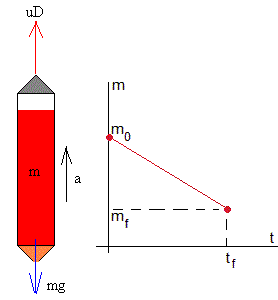
Suponemos que la cantidad de combustible quemado en la unidad de tiempo, D, es constante, D=-dm/dt. La masa m del cohete en el instante t valdrá m=m₀-D·t. Donde m₀ es la suma de la carga útil más el combustible inicial, y D·t es el combustible quemado al cabo de un cierto tiempo t.

El combustible se agota en el tiempo t_f y la masa final del cohete es m_f=m₀-Dt_f

$m \frac{d v}{d t} = u D - m g$

Un cohete puede considerarse una partícula de masa variable m sometida a dos fuerzas de la misma dirección pero de sentidos contrarios: el empuje de los gases uD y el peso mg.

Escribimos la ecuación del movimiento para t<t_f

$\frac{d v}{d t} = - g + u \frac{D}{m_{0} - D t}$

Que se puede integrar de forma inmediata

$\int_{v_{0}}^{v} d v = \int_{0}^{t} (- g + u \frac{D}{m_{0} - D t}) d t$

obteniéndose la expresión de la velocidad en función del tiempo

$v = v_{0} - g t + u \cdot \ln \frac{m_{0}}{m_{0} - D t}$

Volviendo a integrar

$x - x_{0} = \int_{0}^{t} v \cdot d t$

Se obtiene la posición x del móvil en cualquier instante t.

Teniendo en cuanta el resultado de la integral

$\int \ln x \cdot d x = x \ln x - x$

La posición del móvil es

$x = x_{0} + (v_{0} + u) t - \frac{1}{2} g t^{2} + \frac{u}{D} (m_{0} - D t) \ln (1 - \frac{D t}{m_{0}})$

Ejemplos

El empuje es mayor que peso

Combustible total en el cohete, 1.0 kg
Carga útil que transporta, 2.0 kg
Combustible quemado por segundo, D=0.1 kg/s
Velocidad de salida de los gases u=1000 m/s

Se considera despreciable la masa del recipiente que contiene el combustible

Fuerzas sobre el cohete

Masa total del cohete=carga útil+combustible

m₀=2.0+1.0=3.0 kg

El peso del cohete m₀·g (29.4 N) es menor que el empuje u·D (100 N)

Tiempo que tarda en agotarse el combustible

Como hay 1.0 kg de combustible que se queman a razón de 0.1 kg/s. Luego, el combustible se agota en el instante t_f=10 s.

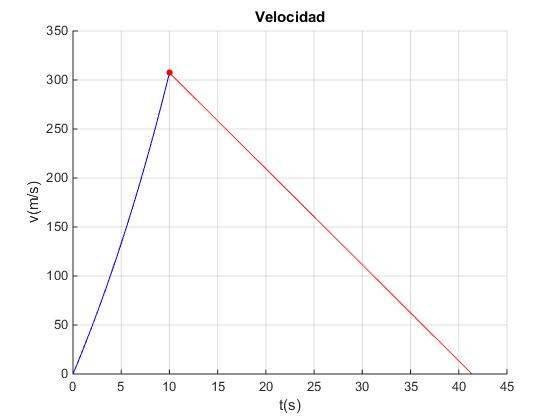
Velocidad máxima alcanzada por el cohete

v_f=307 m/s

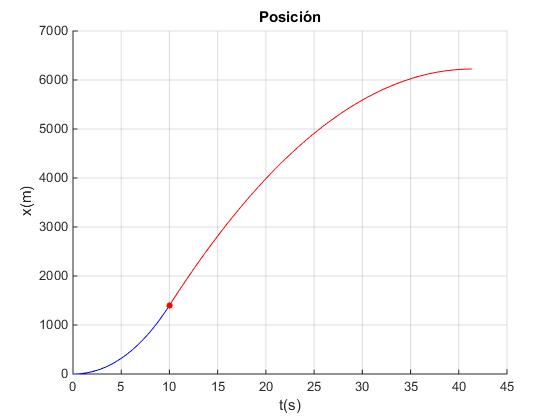
Altura que alcanza hasta que se agota el combustible

x_f=1400 m

Una vez que ha agotado el combustible, el cohete prosigue su movimiento hasta que alcanza la máxima altura. Las ecuaciones del movimiento son

$\begin{array}{l} v = v_{f} - g (t - t_{f}) \\ x = x_{f} + v_{f} (t - t_{f}) - \frac{1}{2} g {(t - t_{f})}^{2} \end{array}$

Donde x_f, v_f es la posición, velocidad del cohete en el instante t_f=10 s en el que se ha agotado el combustible.

La altura máxima se alcanza cuando v=0, en el instante t=41.4 s. La posición del cohete en dicho instante es x=6223 m.

El empuje es menor que peso

Combustible total en el cohete, 2.0 kg
Carga útil que transporta, 9.0 kg
Combustible quemado por segundo, D=0.1 kg/s
Velocidad de salida de los gases u₀=1000 m/s

Se considera despreciable la masa del recipiente que contiene el combustible

Fuerzas sobre el cohete

El peso del cohete (2.0+9.0)·9.8=107.8 N es mayor que el empuje u·D=1000·0.1=100 N

Se va quemando el combustible sin que se mueva el cohete hasta el momento en el que el peso se iguala al empuje.

(c+9)·9.8=100

Cuando el combustible c=1.204 kg el cohete empieza a elevarse. Se han desperdiciado 2-1.204=0.796 kg de combustible.

Masa inicial del cohete al despegue

m₀=1.204+9.0=10.204 kg

Tiempo que tarda en agotarse el combustible

Como hay 1.204 kg de combustible que se queman a razón de 0.1 kg/s. Luego, el combustible se agota en 12.04 s.

Velocidad máxima alcanzada por el cohete

v_f=7.56 m/s

Altura que alcanza hasta que se agota el combustible

x_f=29.62 m

Tiempo que tarda en alcanzar la máxima altura

0=7.56-9.8(t-12.04)
t=12.8 s

Posición del cohete en dicho instante

x=29.62+7.56·0.77-4.9·0.77²=32.5 m

u=1000; %velocidad de escape de los gases (respecto al cohete)
combustible=1; %combustible
carga=2;  %carga útil
m0=carga+combustible; %masa total
D=0.1; %kg de combustible quemado por segundo
t0=combustible/D; %tiempo hasta que se agota el combustible
v0=-9.8*t0+u*log(m0/(m0-D*t0)); %velocidad final
x0=-4.9*t0^2+u*t0+u*(m0-D*t0)*log(1-D*t0/m0)/D;
fprintf('Velocidad final %4.1f, posición final %5.1f\n',v0,x0);
t1=v0/9.8;  %hasta que alcanza la máxima altura
 
figure
hold on
v=@(t) -9.8*t+u*log(m0./(m0-D*t));
fplot(v,[0,t0],'color','b')
fplot(@(t) v0-9.8*(t-t0),[t0,t1+t0],'color','r')
plot(t0,v0,'ro','markersize',3,'markerfacecolor','r')
hold off
grid on
xlabel('t(s)')
ylabel('v(m/s)')
title('Velocidad')
 
figure
hold on
x=@(t) -4.9*t.^2+u*t+u*(m0-D*t).*log(1-D*t/m0)/D;
fplot(x,[0,t0],'color','b')
fplot(@(t) x0+v0*(t-t0)-4.9*(t-t0).^2,[t0,t0+t1],'color','r')
plot(t0,x0,'ro','markersize',3,'markerfacecolor','r')
hold off
grid on
xlabel('t(s)')
ylabel('x(m)')
title('Posición')

Velocidad final 307.5, posición final 1400.7

Actividades

Se introduce:

Combustible total en el cohete, en el control titulado Combustible total en el cohete
Carga útil que transporta, en el control titulado Carga útil que transporta
Combustible quemado por segundo, en el control titulado Combustible quemado por seg.
Velocidad de salida de los gases u₀=1000 m/s

Se pulsa el botón titulado Nuevo

Al lado del cohete, dos flechas, se dibujan las fuerzas sobre el cohete: en color rojo el empuje y en color azul el peso. El empuje permanece constante, el peso va disminuyendo a medida que se va quemando el combustible.

Si el peso inicial del cohete (carga útil más combustible) m₀·g es mayor que el empuje proporcionado por la expulsión de los gases u·D, el cohete quema el combustible sin despegar, hasta el momento en el que el peso se hace igual o menor que el empuje.

Una vez que despega, el cohete agota el combustible en el instante t, cociente entre la masa combustible y el combustible quemado por segundo.

La velocidad que alcanza el cohete cuando agota el combustible se obtiene mediante la fórmula

$v = - 9.8 \cdot t + u \ln \frac{m_{0}}{m_{0} - D t}$

donde m₀ es la masa del cohete al despegar y t es el tiempo desde que despega hasta que agota el combustible. Después, el cohete continúa ascendiendo hasta que su velocidad se hace cero.

En la parte derecha, se representa la velocidad del cohete en función del tiempo.
En la parte izquierda, observamos la altura del cohete en función del tiempo.

Combustible total en el cohete (kg)<2
Combustible quemado por seg (kg/s) <1
Carga útil <10

Caso general

Consideremos el movimiento vertical de un cohete teniendo en cuenta que la gravedad disminuye con la altura y que experimenta un fuerza de rozamiento proporcional al cuadrado de la velocidad

Variación de la aceleración de la gravedad con la altura

La aceleración de la gravedad g a una altura x sobre la superficie de la Tierra mide la fuerza con que la Tierra atrae a una unidad de masa

$g = G \frac{M}{{(R + x)}^{2}} = g_{0} \frac{R^{2}}{{(R + x)}^{2}}$

Donde g₀=9.8 m/s² es la aceleración de la gravedad en la superficie de la Tierra

Se denomina velocidad de escape, v_e, a la velocidad mínima necesaria con la que tendríamos que lanzar un cuerpo desde la superficie de la Tierra para que llegara al infinito con velocidad nula

$\begin{array}{l} \frac{1}{2} m v_{e}^{2} - G \frac{M m}{R} = 0 \\ v_{e} = \sqrt{2 G \frac{M}{R}} = \sqrt{2 g_{0} R} \end{array}$

Siendo R=6370 km el radio de la Tierra, la velocidad de escape es v_e=11174 m/s

Fuerza de rozamiento

Cuando un cuerpo se mueve en el seno de un fluido experimenta una fuerza de rozamiento que es proporcional a la densidad del fluido y al cuadrado de su velocidad

$F_{r} = C_{D} \frac{1}{2} ρ_{f} A v^{2}$

Donde C_D se denomina coeficiente de arrastre, ρ_f es la densidad del fluido, A es el área de la sección transversal a la dirección del movimiento y v es la velocidad relativa del objeto respecto del fluido. Para números de Reynolds grandes C_D es aproximadamente constante

La densidad del aire ρ_f en la atmósfera disminuye con la altura, el modelo más simple (la atmósfera isoterma) predice una disminución exponencial con la altura.

$ρ_{f} = ρ_{0} \exp (- x / H)$

Donde H es una constante.

La fuerza de rozamiento es

$F_{r} = k \exp (- x / H) {(\frac{d x}{d t})}^{2}$

Donde k es una constante que agrupa a varios factores

Ecuación del movimiento

La ecuación del movimiento del cohete se escribe

$m \frac{d v}{d t} = - m g - F_{r} + u D$

En forma de ecuación diferencial

$\frac{d^{2} x}{d t^{2}} = - g_{0} \frac{R^{2}}{{(R + x)}^{2}} + \frac{u D - k \exp (- x / H) {(\frac{d x}{d t})}^{2}}{m_{0} - D t}$

Resolvemos la ecuación del movimiento para los siguientes valores de los parámetros

Radio de la Tierra, R=6.37·10⁶ m
Aceleración de la gravedad en la superficie de la Tierra, g₀=9.8 m/s²
Masa del cohete, m₀=10 000 kg
Masa del combustible, m_f=0.9·m₀ (90 por ciento)
Tiempo de encendido del cohete hasta que se agota el combustible, t_f=300 s
Velocidad de escape de los gases u=5000 m/s, relativa al cohete
Constante H=7462 m
Constante k=2 kg/m

El empuje de los gases es uD, donde D=m_f/t_f es el combustible quemado en la unidad de tiempo

Elaboramos un script para resolver la ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=0, x=0, y dx/dt=0. Parte del reposo desde la superficie de la Tierra

Se resuelve la ecuación diferencial hasta que se agota el combustible en el instante t_f, a partir del cual el cohete disminuye su velocidad con la altura

Representamos en función del tiempo t/t_f

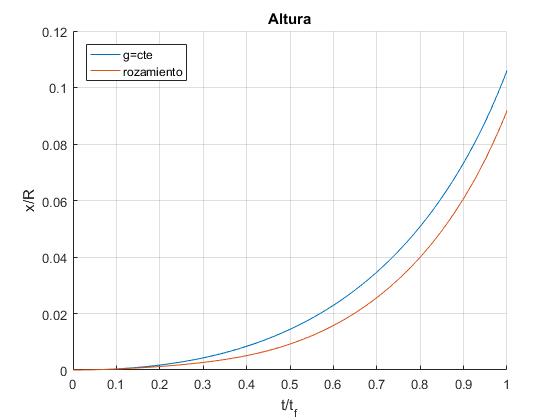
La altura, x/R, donde R es el radio de la Tierra
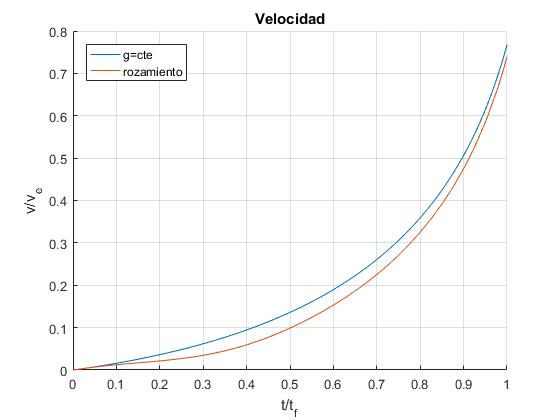
La velocidad, v/v_e, siendo v_e la velocidad de escape

Comparamos el movimiento vertical de un cohete con aceleración de la gravedad constante g₀, con el mismo cohete suponiendo que la aceleración de la gravedad disminuye con la altura y además el aire de una atmósfera isoterma ejerce una fuerza de rozamiento proporcional al cuadrado de la velocidad

R=6370000; %radio de la Tierra
m0=10000; %masa inicial
mf=9*m0/10; %combustible el 90%
tf=300; %duración combustible
u=5000; %velocidad de los gases relativa al cohete
k=2;
H=7462; 

f=@(t,x) [x(2);-9.8*R^2/(R+x(1))^2-(k*exp(-x(1)/H)*x(2)^2-mf*u/tf)/(m0-mf*t/tf)]; 
[t,x]=ode45(f,[0,tf],[0,0]);
hold on
xx=@(t) -4.9*t.^2+u*t*log(m0)+u*tf*((m0-mf*t/tf).*log(m0-mf*t/tf)+
mf*t/tf-m0*log(m0))/mf;
tt=linspace(0,tf,100);
plot(tt/tf,xx(tt)/R);
plot(t/tf,x(:,1)/R)
hold off
grid on
legend('g=cte','rozamiento','location','northwest')
xlabel('t/t_f')
ylabel('x/R');
title('Altura')

figure
hold on
v=@(t) -9.8*t+u*log(m0./(m0-mf*t/tf));
plot(tt/tf,v(tt)/sqrt(2*9.8*R));
plot(t/tf,x(:,2)/sqrt(2*9.8*R))
hold off
grid on
legend('g=cte','rozamiento','location','northwest')
xlabel('t/t_f')
ylabel('v/v_e');
title('Velocidad')

Presión dinámica

La presión dinámica se define

$Q = \frac{1}{2} (ρ_{0} e^{- x / H}) v^{2}$

Entre paréntesis, la densidad del aire que disminuye exponencialmente con la altura, ρ₀=1.29 kg/m³ es la densidad del aire a nivel del mar, v es la velocidad del cohete. Dado que la densidad disminuye y la velocidad del cohete aumenta, a una altura x o en un instante t, la presión dinámica Q alcanza un valor máximo. Los misiles, cohetes , etc, se diseñan para que aguanten hasta un máximo de presión o en caso contrario, podrían sufir daños estructurales.

Representamos la presión dinámica Q en Pa en función del tiempo t/t_f

R=6370000; %radio de la Tierra
m0=10000; %masa inicial
mf=9*m0/10; %combustible el 90%
tf=300; %duración combustible
u=5000; %velocidad de los gases relativa al cohete
k=2;
H=7462; 

f=@(t,x) [x(2);-9.8*R^2/(R+x(1))^2-(k*exp(-x(1)/H)*x(2)^2-mf*u/tf)/(m0-mf*t/tf)]; 
[t,x]=ode45(f,[0,tf],[0,0]);

p=1.29*exp(-x(:,1)/H).*x(:,2).^2/2;
plot(t/tf,p);
grid on
xlabel('t/t_f')
ylabel('Q (Pa)')
title('Presión')

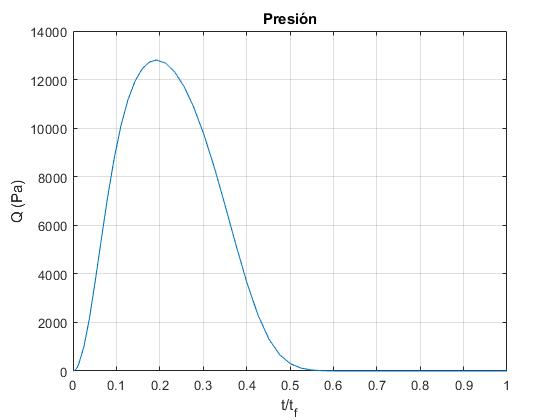
La presión dinámica máxima max(p) se produce en el instante t=57.8 s, a una altura de x=7.4 km. Poco tiempo después de despegar

>> [p,indice]=max(p)
p =   1.2805e+04
indice =    45
>> t(indice)
ans =   57.8450
>> x(indice,1)/1000
ans =    7.3794

Vuelo del Discovery STS-119

Algunos datos del vuelo

Tiempo (s)	Altura (m)	v (m/s)	v_y (m/s)	v_x (m/s)
0	-7	0	0	0
5	46	24	24	0
10	236	55	55	0
15	672	97	95	19
18	976	120	115	34
20	1 211	137	129	46
30	2 787	220	197	97
36	4 032	266	234	126
40	5 214	300	257	154
50	7 890	364	300	206
60	11 380	454	363	272
90	25 496	882	576	667
120	44 626	1 324	660	1 147
124	47 341	1 339	644	1 173
125	48 162	1 341	643	1 176
150	63 018	1 483	545	1 379
180	77 732	1 696	437	1 638
210	89 304	1 957	334	1 928
240	97 930	2 258	340	2 232
260	104 006	2 614	151	2 609
300	107 416	3 007	74	3 006
330	108 715	3 452	10	3 451

La fuerza de rozamiento que ejerce el aire sobre el cohete que asciende durante los primeros 60 s de vuelo hasta 11 km de altura, se puede aproximar por

$F_{r} = C_{D} \frac{1}{2} ρ_{f} A v^{2}$

La densidad del aire no es constante

El modelo de atmósfera hasta una altura de 11 km es

$ρ_{f} = ρ_{0} {(1 - \frac{h}{h_{0}})}^{n}$

donde ρ=1.225 kg/m³ es la densidad del aire al nivel del mar, h₀=44 330 m, y n=4.256.

Los datos de la velocidad v del cohete se ajustan a una línea recta v=r·t+s

t=[0,5,10,15,18,20,30,36,40,50,60];
v=[0,24,55,97,120,137,220,266,300,364,454];
plot(t,v,'ro','markersize',4,'markerfacecolor','r')
xlabel('t(s)')
ylabel('v(m/s)')
title('Módulo de la velocidad')
grid on

En el menú, seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla Linear

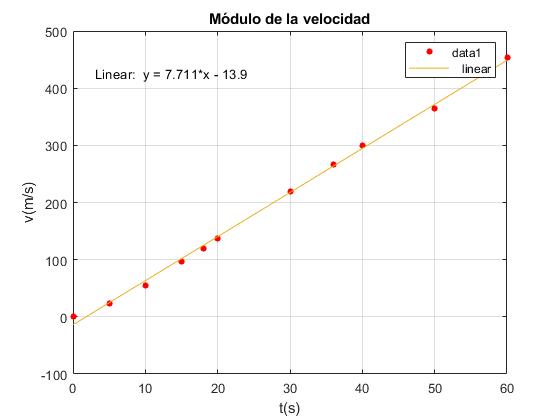
Los resultados son: r=7.711, s=-13.9

Los datos de la altura h del cohete se ajustan a una parábola h=at²+bt+c

t=[0,5,10,15,18,20,30,36,40,50,60];
h=[-7,46,236,672,976,1211,2787,4032,5214,7890,11380];
plot(t,h,'ro','markersize',4,'markerfacecolor','r')
xlabel('t(s)')
ylabel('h(m)')
title('Altura')
grid on

En el menú, seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla Quadratic

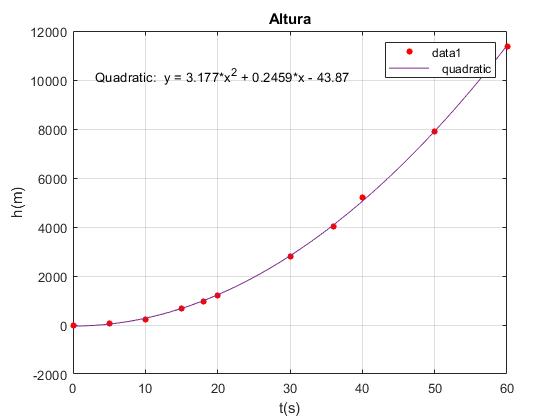
Los resultados son: a=3.177, b=0.2459, c=-43.87

La expresión de la fuerza de rozamiento en función del tiempo t es

$F_{r} = \frac{1}{2} C_{D} ρ_{0} {(1 - \frac{a t^{2} + b t + c}{h_{0}})}^{n} A {(r t + s)}^{2}$

El valor máximo de F_r se obtiene derivando con respecto del tiempo e igualando a cero

$\begin{array}{l} \frac{d F_{r}}{d t} = \frac{1}{2} C_{D} ρ_{0} A {(- \frac{2 a t + b}{h_{0}}) n {(1 - \frac{a t^{2} + b t + c}{h_{0}})}^{n - 1} {(r t + s)}^{2} + {(1 - \frac{a t^{2} + b t + c}{h_{0}})}^{n} 2 r (r t + s)} = 0 \\ (- \frac{2 a t + b}{h_{0}}) n (r t + s) + (1 - \frac{a t^{2} + b t + c}{h_{0}}) 2 r = 0 \\ (2 n a r + 2 r a) t^{2} + (2 n a s + n r b + 2 r b) t + n b s + 2 r c - 2 r h_{0} = 0 \end{array}$

Obtenemos la ecuación de segundo grado

$(2 n a r + 2 r a) t^{2} + (2 n a s + n r b + 2 r b) t + n b s + 2 r c - 2 r h_{0} = 0$

Cuya raíz real positiva nos da el instante t=52.3 s (el cohete se encuentra a una altura de 8 650 m), para el cual la fuerza de rozamiento F_r es máxima

n=4.256;
h0=44330;
a=3.177;
b=0.2559;
c=-43.87;
r=7.711;
s=-13.9;
A=2*n*a*r+2*r*a; %coeficientes de la ecuación de segundo grado
B=2*n*a*s+n*r*b+2*r*b;
C=n*b*s+2*r*c-2*r*h0;
tm=(-B+sqrt(B^2-4*A*C))/(2*A); %raíz real positiva
disp(tm)

52.2611
>> a*tm^2+b*tm+c
ans =   8.6466e+03

Referencias

O.L. de Lange, J. Pierrus. Solved Problems in Classical Mechanics. Analytical and numerical solutions with comments. Oxford University Press (2010). Question 11.28, pp. 382-384

Philip Backman. Maximum Aerodynamic Force on an Ascending Space Vehicle. The Physics Teacher. Vol. 50, March 2012. pp. 167-169

Arthur Stinner, Don Metz. The Flight of the Space Shuttle Discovery (STS-119). The Physics Teacher. Vol. 48, March 2010. pp. 162-168