Los calamares nadan por propulsión a chorro: absorben agua hacia el interior de su cavidad paleal, a través de aberturas situadas a cada lado de la cabeza, y la expulsan a alta presión por un sifón. Tienen la forma adecuada, hidrodinámica, que les permite moverse con gran velocidad. Los pulpos utilizan sus tentáculos para moverse por el lecho marino y emplean la propulsión a chorro solamente en situaciones de emergencia.

Supondremos que una masa m de fluido en reposo se absorbe hacia el interior de la cavidad del dispositivo (un calamar, un pulpo, un avión) de masa M, la masa de fluido m se expulsa con velocidad u relativa al dispositivo. La duración de este proceso (un pulso) es muy pequeña comparada con el intervalo τ entre dos pulsos consecutivos.

Dado que el empuje actúa en sentido contrario al peso, incluiremos su efecto reduciendo el valor de la aceleración de la gravedad g₀. La aceleración de la gravedad efectiva g de un cuerpo sumergido en el seno de un fluido será

${\displaystyle g=\left(1-\frac{{\rho }_f}{{\rho }_s}\right)g_0}$

Donde g₀=9.8 m/s², ρ_f es la densidad del fluido y ρ_s es la densidad del cuerpo sumergido, véase la página titulada 'Viscosidad de un fluido'

En la descripción del movimiento del dispositivo no incluiremos inicialmente el rozamiento, que siempre existirá cuando un cuerpo se mueve en el seno de un fluido. Las ecuaciones del movimiento de un cuerpo que se mueve verticalmente con aceleración constante g son

${\displaystyle \begin{array}{l}v=v_0-gt\\ y=y_0+v_{0}t-\frac{1}{2}g{t}^2\end{array}}$

Modelo de la propulsión a chorro

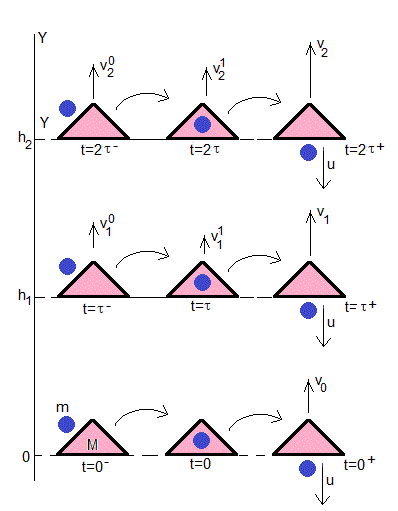
Primer pulso, n=0

El dispositivo de masa M se encuentra en reposo en el origen en el instante inicial t=0. Absorbe una cantidad m de fluido en reposo en el instante t=0^- y la expulsa con velocidad u relativa al dispositivo en el instante t=0⁺, adquiriendo el dispositivo una velocidad v₀. Aplicamos el principio de conservación del momento lineal

${\displaystyle \begin{array}{l}0=M{v}_0+m(-u)\\ v_0=fu,f=\frac{m}{M}\end{array}}$

Movimiento entre el primer pulso (n=0) y el segundo (n=1)

Entre los instantes t=0⁺ y t=τ^-, el dispositivo asciende disminuyendo su velocidad e incrementado su altura. Utilizamos las ecuaciones del movimiento uniformemente acelerado para determinar su velocidad y altura en el instante t=τ^-.

${\displaystyle \begin{array}{l}{v}_1^0=v_0-g\tau \\ h_1=v_0\tau -\frac{1}{2}g{\tau }^2\end{array}}$

Segundo pulso, n=1

En el instante t=τ^-, el dispositivo de masa M y velocidad $v_1^0$ , absorbe una masa m de fluido en reposo, proceso que describimos mediante la ecuación de un choque completamente inelástico

${\displaystyle M{v}_1^0=(m+M)v_1^1}$

la velocidad $v_1^1$ del conjunto disminuye

En el instante t=τ⁺ el dispositivo expulsa la masa m de fluido con velocidad u relativa al dispositivo o $-u+v_1^1$, relativa al Sistema de Referencia con origen en O. La velocidad del dispositivo aumenta a v₁. Aplicamos el principio de conservación del momento lineal

${\displaystyle \begin{array}{l}(m+M)v_1^1=M{v}_1+m\left(-u+v_1^1\right)\\ v_1=\frac{M{v}_1^1+mu}{M}=\frac{M}{m+M}{v}_1^0+\frac{m}{M}u=\frac{v_0-g\tau }{1+f}+fu\end{array}}$

Movimiento entre el segundo pulso (n=1) y el tercero (n=2)

Entre los instantes t=τ⁺ y t=2τ^-, el dispositivo asciende disminuyendo su velocidad e incrementado su altura. Utilizamos las ecuaciones del movimiento uniformemente acelerado para determinar su velocidad y altura en el instante t=2τ^-.

${\displaystyle \begin{array}{l}{v}_2^0=v_1-g\tau \\ h_2=h_1+v_1\tau -\frac{1}{2}g{\tau }^2\end{array}}$

Tercer pulso, n=2

En el instante t=2τ^-, el dispositivo de masa M y velocidad $v_2^0$ , absorbe una masa m de fluido en reposo, proceso que describimos mediante la ecuación de un choque completamente inelástico

${\displaystyle M{v}_2^0=(m+M)v_2^1}$

la velocidad $v_2^1$ del conjunto disminuye

En el instante t=2τ⁺ el dispositivo expulsa la masa m de fluido con velocidad u relativa al dispositivo o $-u+v_2^1$, relativa al Sistema de Referencia con origen en O. La velocidad del dispositivo aumenta a v₂. Aplicamos el principio de conservación del momento lineal

${\displaystyle \begin{array}{l}(m+M)v_2^1=M{v}_2+m\left(-u+v_2^1\right)\\ v_2=\frac{M{v}_2^1+mu}{M}=\frac{M}{m+M}{v}_2^0+\frac{m}{M}u=\frac{v_1-g\tau }{1+f}+fu\end{array}}$

Movimiento entre el tercer pulso (n=2) y el cuarto (n=3)

Entre los instantes t=2τ⁺ y t=3τ^-, el dispositivo asciende disminuyendo su velocidad e incrementado su altura. Utilizamos las ecuaciones del movimiento uniformemente acelerado para determinar su velocidad y altura en el instante t=3τ^-.

${\displaystyle \begin{array}{l}{v}_3^0=v_2-g\tau \\ h_3=h_2+v_2\tau -\frac{1}{2}g{\tau }^2\end{array}}$

Pulso, n

La velocidad en el instante t=n·τ⁺ será

${\displaystyle v_n=\frac{v_{n-1}-g\tau }{1+f}+fu,v_0=fu}$

La altura en el instante t=n·τ o tras n+1 pulsos, será

${\displaystyle h_n=h_{n-1}+v_{n-1}\tau -\frac{1}{2}g{\tau }^2,h_0=0}$

Las ecuaciones del movimiento del dispositivo en el intervalo t=nτ⁺, t=(n+1)τ^-, entre los pulsos n y n+1, son

${\displaystyle \begin{array}{l}v=v_n-g\left(t-n\tau \right),n\tau \le t<(n+1)\tau \\ y=h_n+v_n\left(t-n\tau \right)-\frac{1}{2}g{\left(t-n\tau \right)}^2\end{array}}$

Ejemplo

Representamos la velocidad y la altura del dispositivo en función del tiempo para el siguiente caso:

• El cociente f=1/3 entre las masas m (de fluido expulsado) y M (del dispositivo),
• El intervalo de tiempo τ=10.85 s entre dos pulsos consecutivos
• La velocidad u=9.4 m/s de la porción de masa m de fluido expulsada, relativa al dispositivo
• La aceleración g=0.38 m/s² de la gravedad efectiva de un cuerpo sumergido en un fluido

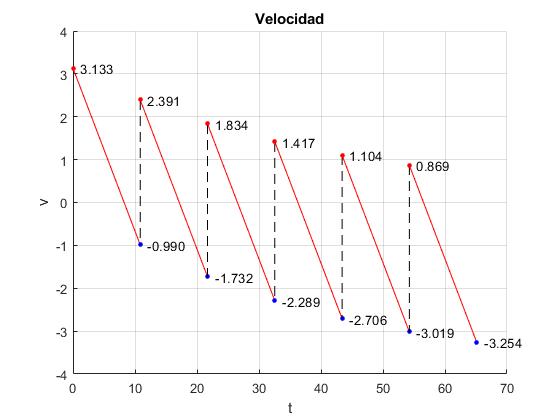
En la parte superior, tenemos las velocidades v_n, inmediatamente después de expulsar la porción de masa m. En la parte inferior, las velocidades finales en el instante nτ, o las velocidades iniciales $v_{n+1}^0$, al comienzo del siguiente pulso. La relación es

${\displaystyle v_{n+1}^0=v_n-g\tau ,n=\mathrm{0,1,2,3....}}$

u=9.4; %velocidad del fluido relativa al dispositivo
g=0.38; %aceleración de la gravedad efectiva
f=1/3; %cociente masas m/M
tau=10.85;  %intervalo entre dos pulsos consecutivos
v0=f*u;
func=@(t) v0-g*t;
hold on
fplot(func,[0,tau],'color','r')
plot(tau,func(tau),'o','markersize',3,'markeredgecolor','b','markerfacecolor','b') 
text(tau,func(tau), sprintf('  %1.3f',func(tau)))
plot(0,v0,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r') 
text(0,v0, sprintf('  %1.3f',v0))
for i=1:5
     v=(v0-g*tau)/(1+f)+f*u;
     line([i*tau,i*tau],[v,func(i*tau)],'lineStyle','--', 'color','k')
    func=@(t) v-g*(t-i*tau);
    fplot(func,[i*tau,(i+1)*tau], 'color','r')
    plot(i*tau,v,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r') 
    text(i*tau,v, sprintf('  %1.3f',v))
    plot((i+1)*tau,func((i+1)*tau),'o','markersize',3,'markeredgecolor',
'b','markerfacecolor','b') 
    text((i+1)*tau,func((i+1)*tau), sprintf('  %1.3f',func((i+1)*tau)))
    v0=v;
end
hold off
grid on
xlabel('t')
ylabel('v')
title('Velocidad')

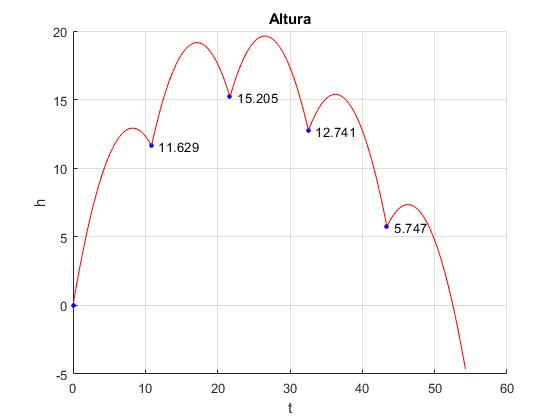
En la figura, se proporcionan los datos de la altura del dispositivo en el instante nτ. En un instante comprendido entre 4τ y 5τ regresa al origen.

u=9.4; %velocidad del fluido relativa al dispositivo
g=0.38; %aceleración de la gravedad efectiva
f=1/3; %cociente masas m/M
tau=10.85;  %intervalo entre dos pulsos consecutivos
v0=f*u;
func=@(t) v0*t-g*t.^2/2;
hold on
fplot(func,[0,tau],'color','r')
plot(0,0,'o','markersize',3,'markeredgecolor','b','markerfacecolor','b') 
h0=v0*tau-g*tau^2/2;
for i=1:4
    plot(i*tau,h0,'o','markersize',3,'markeredgecolor','b','markerfacecolor','b') 
    text(i*tau,h0, sprintf('  %1.3f',h0))
    v=(v0-g*tau)/(1+f)+f*u;
    func=@(t) h0+v*(t-i*tau)-g*(t-i*tau).^2/2;
    fplot(func,[i*tau,(i+1)*tau], 'color','r')
    h0=h0+v*tau-g*tau^2/2;
    v0=v;
end
hold off
grid on
xlabel('t')
ylabel('h')
title('Altura')

Velocidad

Expresamos v_n como función explícita de n

${\displaystyle \begin{array}{l}{v}_1=\left(1+\frac{1}{1+f}\right)fu-g\tau \left(\frac{1}{1+f}\right)\\ v_2=\left(1+\frac{1}{1+f}+\frac{1}{{\left(1+f\right)}^2}\right)fu-g\tau \left(\frac{1}{1+f}+\frac{1}{{\left(1+f\right)}^2}\right)\\ \mathrm{....}\\ v_n=\left(1+\frac{1}{1+f}+\frac{1}{{\left(1+f\right)}^2}+\mathrm{...}\frac{1}{{\left(1+f\right)}^n}\right)fu-\frac{g\tau }{1+f}\left(1+\frac{1}{1+f}+\mathrm{...}\frac{1}{{\left(1+f\right)}^{n-1}}\right)\end{array}}$

Los paréntesis contienen la suma de los términos de una progresión geométrica de razón 1/(1+f),

${\displaystyle \begin{array}{l}{v}_n=\frac{\frac{1}{{\left(1+f\right)}^{n+1}}-1}{\frac{1}{1+f}-1}fu-\frac{g\tau }{1+f}\left(\frac{\frac{1}{{\left(1+f\right)}^n}-1}{\frac{1}{1+f}-1}\right)\\ v_n=\left(f+1-\frac{1}{{\left(1+f\right)}^n}\right)u-\frac{g\tau }{f}\left(1-\frac{1}{{\left(1+f\right)}^n}\right)\end{array}}$

Cuando n se hace muy grande, la velocidad tiende hacia un límite v_∞.

${\displaystyle v_{\infty }=\underset{n\to \infty }{\lim }{v}_n=(1+f)u-\frac{g\tau }{f}}$

Esta velocidad es positiva si

${\displaystyle \tau <\frac{(1+f)fu}{g}}$

Cuando τ=fu/g, v_∞=fu, que es la velocidad inicial de partida del dispositivo

Ejemplo

• La densidad de un pulpo es un 4% mayor que el agua, el efecto del empuje del agua es importante, la aceleración de la gravedad efectiva será

${\displaystyle g=\left(1-\frac{1}{1.04}\right)9.8=0.38{\text{m/s}}^{\text{2}}}$

• El cociente entre la masa m de agua que absorbe y expulsa y la masa del pulpo M es f=0.2/0.6=1/3.

• La velocidad u del agua expulsada por el sifón relativa al pulpo es 9.4 m/s

Para que v_∞>0, τ<10.9942

Representamos las velocidades v_n (n=0,1,2...20) del pulpo en los instantes t=n·τ⁺, para los siguientes intervalos τ, 10.85 (rojo), fu/g=8.25 (negro), 7 (azul)

• Utilizando la expresión de v_n en términos de n

u=9.4; %velocidad del agua relativa al pulpo
g=0.38; %aceleración de la gravedad efectiva en el agua
f=1/3; %cociente m/M, agua expulsada/masa pulpo
color=['r','k','b'];
k=1;
hold on
for tau=[10.85,f*u/g,7]   %intervalo entre dos pulsos consecutivos
    for i=0:20
        v=(f+1-1/(1+f)^i)*u-g*tau*(1-1/(1+f)^i)/f;
        plot(i,v,'o','markersize',3,'markeredgecolor',color(k),
'markerfacecolor',color(k))
    end
    k=k+1;
end
hold off
grid on
xlabel('n')
ylabel('v')
title('Velocidad')

• Utilizando las relaciones de recurrencia

u=9.4; %velocidad del agua relativa al pulpo
g=0.38; %aceleración de la gravedad efectiva en el agua
f=1/3; %cociente m/M, agua expulsada/masa pulpo
color=['r','k','b'];
k=1;
hold on
for tau=[10.85,f*u/g,7]  %intervalo entre dos pulsos consecutivos
    v0=f*u;
    plot(0,v0,'o','markersize',3,'markeredgecolor',color(k),
'markerfacecolor',color(k))
    for i=1:20
        v=(v0-g*tau)/(1+f)+f*u;
        plot(i,v,'o','markersize',3,'markeredgecolor',color(k),
'markerfacecolor',color(k))
        v0=v;
    end
    k=k+1;
end
hold off
grid on
xlabel('n')
ylabel('v')
title('Velocidad')

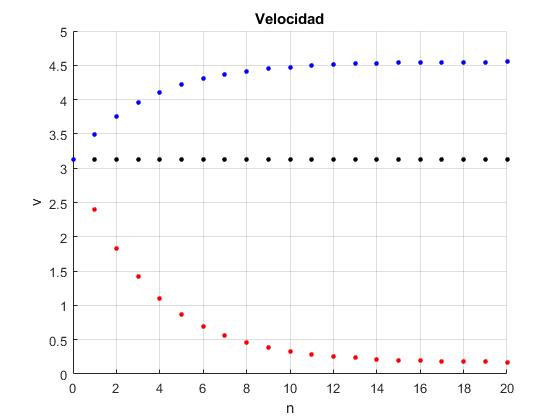
Para τ=10.85, la velocidad decrece, para τ=8.25, la velocidad se mantiene constante, para τ=7, la velocidad crece, tendiendo al valor asintótico

>> (1+f)*u-g*tau/f
ans =    4.5533

Alturas

Más complicado resulta expresar la altura h_n en términos de n

${\displaystyle \begin{array}{l}{h}_1=fu\tau -\frac{g{\tau }^2}{2}\\ h_2=\left(2+\frac{1}{1+f}\right)fu\tau -g{\tau }^2\left(1+\frac{1}{1+f}\right)\\ h_3=\left(3+\frac{2}{1+f}+\frac{1}{{\left(1+f\right)}^2}\right)fu\tau -g{\tau }^2\left(\frac{3}{2}+\frac{2}{1+f}+\frac{1}{{\left(1+f\right)}^2}\right)\\ h_4=\left(4+\frac{3}{1+f}+\frac{2}{{\left(1+f\right)}^2}+\frac{1}{{\left(1+f\right)}^3}\right)fu\tau -g{\tau }^2\left(2+\frac{3}{1+f}+\frac{2}{{\left(1+f\right)}^2}+\frac{1}{{\left(1+f\right)}^3}\right)\\ \mathrm{....}\\ h_n=\left(n+{\displaystyle \sum _{k=1}^{n-1}\frac{n-k}{{\left(1+f\right)}^k}}\right)fu\tau -g{\tau }^2\left(\frac{n}{2}+{\displaystyle \sum _{k=1}^{n-1}\frac{n-k}{{\left(1+f\right)}^k}}\right)\end{array}}$

Utilizamos la función symsum de Math Symbolic de MATLAB para obtener la suma de la serie

>> syms n k a;
>> symsum((n-k)/a^k,k,1,n-1)
ans =piecewise(a == 1, (n*(n - 1))/2, 
a ~= 1, a/(a^n*(a - 1)^2) - (a + n - a*n)/(a - 1)^2)

donde la variable simbólica a=1+f

${\displaystyle {\displaystyle \sum _{k=1}^{n-1}\frac{n-k}{a^k}}=\frac{a}{a^n{\left(a-1\right)}^2}-\frac{a+n-an}{{\left(a-1\right)}^2}=\frac{1+f}{{\left(1+f\right)}^n{f}^2}-\frac{1+f}{f^2}+n\frac{1+f}{f}}$

La expresión de h_n es

${\displaystyle h_n=\frac{1+f}{f}\left(nf+\frac{1}{{\left(1+f\right)}^n}-1\right)u\tau -\frac{g{\tau }^2}{2f^2}\left(f(f+2)n-2(1+f)\left(1-\frac{1}{{\left(1+f\right)}^n}\right)\right)}$

El dispositivo no regresa al origen si se cumple que para todo n, h_n>0.

${\displaystyle \begin{array}{l}\frac{1+f}{f}\left(nf+\frac{1}{{\left(1+f\right)}^n}-1\right)u\tau >\frac{g{\tau }^2}{2f^2}\left(f(f+2)n-2(1+f)\left(1-\frac{1}{{\left(1+f\right)}^n}\right)\right)\\ \tau <\frac{2f\left(1+f\right)\left(nf+\frac{1}{{\left(1+f\right)}^n}-1\right)u}{g\left(f(f+2)n-2(1+f)\left(1-\frac{1}{{\left(1+f\right)}^n}\right)\right)}\end{array}}$

Dividimos el numerador y el denominador por n, y calculamos el límite cuando n→∞

${\displaystyle \begin{array}{l}\tau <\frac{2f\left(1+f\right)\left(f+\frac{1}{n{\left(1+f\right)}^n}-\frac{1}{n}\right)u}{g\left(f(f+2)-2(1+f)\left(\frac{1}{n}-\frac{1}{n{\left(1+f\right)}^n}\right)\right)}\\ \tau <\frac{2f\left(1+f\right)u}{g(f+2)}\end{array}}$

Si se cumple esta condición el dispositivo no regresará al origen, en caso contrario, resgresará al origen después de n pulsos, que calcularemos más adelante

Con los datos del ejemplo anterior:

• velocidad del agua relativa al pulpo, u=9.4 m/s
• aceleración de la gravedad efectiva en el agua, g=0.38 m/s²
• cociente f=m/M, agua expulsada/masa pulpo, f=1/3,

tenemos, τ<9.42 s

Representamos h_n en función de n para dos valores de τ: 9.3 y 9.6.

• Utilizando la expresión de h_n en términos de n

u=9.4; %velocidad del agua relativa al pulpo
g=0.38; %aceleración de la gravedad efectiva en el agua
f=1/3; %cociente m/M, agua expulsada/masa pulpo
color=['r','b'];
k=1;
hold on
for tau=[9.3,9.6]  %intervalo entre dos pulsos consecutivos
    for i=0:30
        h=(1+f)*(f*i-1+1/(1+f)^i)*u*tau/f-g*tau^2*(f*i*(f+2)-
2*(f+1)*(1-1/(1+f)^i))/(2*f^2);
        plot(i,h,'o','markersize',3,'markeredgecolor',color(k),
'markerfacecolor',color(k))
    end
    k=k+1;
end
hold off
grid on
xlabel('n')
ylabel('h')
title('Alturas')

• Utilizando las relaciones de recurrencia

u=9.4; %velocidad del agua relativa al pulpo
g=0.38; %aceleración de la gravedad efectiva en el agua
f=1/3; %cociente m/M, agua expulsada/masa pulpo
color=['r','b'];
k=1;
hold on
for tau=[9.3,9.6]  %intervalo entre dos pulsos consecutivos
    v0=f*u;
    h0=0;
    plot(0,h0,'o','markersize',3,'markeredgecolor',color(k),
'markerfacecolor',color(k))
    for i=1:30
        h=h0+v0*tau-g*tau^2/2;
        v=(v0-g*tau)/(1+f)+f*u;
        plot(i,h,'o','markersize',3,'markeredgecolor',color(k),
'markerfacecolor',color(k))
        h0=h;
        v0=v;
    end
    k=k+1;
end
hold off
grid on
xlabel('n')
ylabel('h')
title('Alturas')

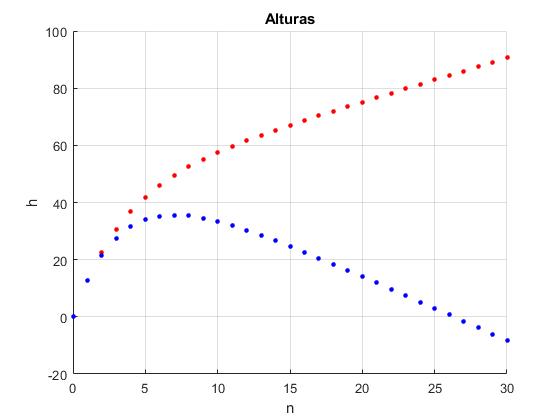
Para τ=9.6>9.42 (color azul), la altura crece y luego, decrece, regresando al origen en un instante comprendido entre 26τ y 27τ. Para τ=9.3<9.42 (color rojo), la altura crece indefinidamente y el dispositivo no regresa al origen

El dispositivo regresa al origen h_n=0, para n solución de la ecuación

${\displaystyle \begin{array}{l}\frac{1+f}{f}\left(nf+\frac{1}{{\left(1+f\right)}^n}-1\right)u\tau -\frac{g{\tau }^2}{2f^2}\left(f(f+2)n-2(1+f)\left(1-\frac{1}{{\left(1+f\right)}^n}\right)\right)=0\\ \frac{1}{{\left(1+f\right)}^n}+\frac{f\left(f(1+f)u-\frac{g\tau }{2}(f+2)\right)}{(fu-g\tau )(1+f)}n=1\\ {\left(1+f\right)}^{-n}=-kn+1\end{array}}$

Es una ecuación del tipo, a^b·x+c=d·x+f con x=n, a=1+f, b=-1, c=0, d=-k, f=1, cuya solución en términos de la función W de Lambert, es

${\displaystyle \begin{array}{l}x=\frac{-1}{b\ln a}W\left(\frac{-b}{d}(\ln a)a^{c-bf/d}\right)-\frac{f}{d}\\ n=\frac{1}{\ln (1+f)}W\left(-\frac{\ln (1+f)}{k{\left(1+f\right)}^{1/k}}\right)+\frac{1}{k}\end{array}}$

u=9.4; %velocidad del agua relativa al pulpo
g=0.38; %aceleración de la gravedad efectiva en el agua
f=1/3; %cociente m/M, agua expulsada/masa pulpo
tau=9.6; %intervalo de tiempo entre dos pulsos consecutivos

k=f*(f*(1+f)*u-g*tau*(f+2)/2)/((1+f)*(f*u-g*tau));
n=lambertw(0,-log(1+f)/(k*(1+f)^(1/k)))/log(1+f)+1/k;
h=@(n) (1+f)*(f*n-1+1/(1+f)^n)*u*tau/f-g*tau^2*(f*n*(f+2)
-2*(f+1)*(1-1/(1+f)^n))/(2*f^2);
disp([n,h(n)])

26.3046   -0.0000

Confirmamos que h_n se hace cero, el dispositivo regresa al origen, en un instante comprendido entre 26τ y 27τ

Actividades

Se introduce

• El cociente f entre las masas m (de fluido) y M (del dispositivo), en el control titulado Cociente masas
• El intervalo de tiempo τ entre dos pulsos consecutivos, en el control titulado Intervalo de tiempo
• La velocidad u de la porción de masa m de fluido expulsada, en el control titulado Velocidad
• La aceleración efectiva g de la gravedad de un cuerpo sumergido en un fluido, en el control titulado Gravedad

Se pulsa el botón titulado Nuevo

Observamos cada uno de los pulsos a intervalos fijos de tiempo: el dispositivo absorbe una porción de masa m de fluido en reposo y lo expulsa a una velocidad u relativa al dispositivo. El dispositivo incrementa su velocidad

En el intervalo entre dos pulsos, el dispostivo se mueve con aceleración constante g hacia abajo

El programa interactivo, nos proporciona los datos:

• Número de pulso, n
• la velocidad, v_n
• la altura, h_n en el pulso n o en el instante nτ
• El tiempo, t
• la altura y del dispositivo entre dos pulsos consecutivos

Representa la altura h del dispositivo en función del tiempo t, hasta que regresa al origen, si lo hace

Con los datos de los ejemplos previos, cuando τ=10.85 s, el pulpo regresa al origen después de n=4 o nτ=43.40 s, en el instante t= 52.52 s, continua en el origen en reposo hasta el instante 5·τ= 54.25, y vuelve a repetir el movimiento. El programa interactivo se detiene en el instante en el que llega al origen.

Fuerza de rozamiento proporcional a la velocidad

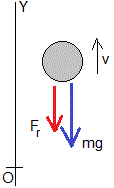
Cuando un cuerpo de forma esférica de densidad ρ_s y radio r, se mueve en un fluido de densidad ρ_f y viscosidad η, la fuerza de rozamiento F_r que se pone al movimiento del cuerpo es

${\displaystyle \begin{array}{l}{F}_r=6\pi \eta rv=kv\\ \gamma =\frac{k}{m}=\frac{9\eta }{2r^2{\rho }_s}\end{array}}$

Esta fórmula, es válida para bajos números de Reynolds, Re

${\displaystyle \mathrm{Re}=\frac{{\rho }_{f}Dv}{\eta }}$

Siendo D=2r la dimensión del dispositivo supuesto de forma esférica

Deducimos las ecuaciones del movimiento de un cuerpo bajo la acción de su peso efectivo (peso menos empuje) y de una fuerza de rozamiento proporcional a la velocidad, sabiendo que en el instante t=0, su velocidad inicial es v₀

${\displaystyle \begin{array}{l}m\frac{dv}{dt}=-mg-kv\\ \frac{dv}{g+\gamma v}=-dt,\gamma =\frac{k}{m}\\ {\displaystyle \underset{v_0}{\overset{v}{\int }}\frac{dv}{g+\gamma v}}=-{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ v=\left(v_0+\frac{g}{\gamma }\right)e^{-\gamma t}-\frac{g}{\gamma }\end{array}}$

Integramos de nuevo para obtener la posición y del objeto sabiendo que en el instante t=0, su altura inicial y₀

${\displaystyle \begin{array}{l}\frac{dy}{dt}=\left(v_0+\frac{g}{\gamma }\right)e^{-\gamma t}-\frac{g}{\gamma }\\ {\displaystyle \underset{y_0}{\overset{y}{\int }}dy}={\displaystyle \underset{0}{\overset{t}{\int }}\left\{\left(v_0+\frac{g}{\gamma }\right)e^{-\gamma t}-\frac{g}{\gamma }\right\}dt}\\ y=y_0+\frac{1}{\gamma }\left(v_0+\frac{g}{\gamma }\right)\left(1-e^{-\gamma t}\right)-\frac{g}{\gamma }t\end{array}}$

Pulso, n

La velocidad en el instante t=n·τ⁺ será

• Sin rozamiento

${\displaystyle v_n=\frac{1}{1+f}\left(v_{n-1}-g\tau \right)+fu,v_0=fu}$

• Con rozamiento

${\displaystyle v_n=\frac{1}{1+f}\left\{\left(v_{n-1}+\frac{g}{\gamma }\right)e^{-\gamma \tau }-\frac{g}{\gamma }\right\}+fu,v_0=fu}$

La altura en el instante t=n·τ o tras n+1 pulsos, será

• Sin rozamiento

${\displaystyle h_n=h_{n-1}+v_{n-1}\tau -\frac{1}{2}g{\tau }^2,h_0=0}$

• Con rozamiento

${\displaystyle h_n=h_{n-1}+\frac{1}{\gamma }\left(v_{n-1}+\frac{g}{\gamma }\right)\left(1-e^{-\gamma \tau }\right)-\frac{g}{\gamma }\tau ,h_0=0}$

Ejemplo 1

Representamos la velocidad y la altura del dispositivo en función del tiempo para el caso estudiado al principio de esta página:

• El cociente f=1/3 entre las masas m (de fluido expulsado) y M (del dispositivo),
• El intervalo de tiempo τ=10.85 s entre dos pulsos consecutivos
• La velocidad u=9.4 m/s de la porción de masa m de fluido expulsada, relativa al dispositivo
• La aceleración g=0.38 m/s² de la gravedad efectiva de un cuerpo sumergido en un fluido
• La constante γ=k/m=0.5 s^-1 de la fuerza de rozamiento proporcional a la velocidad

En la parte superior, tenemos las velocidades v_n, inmediatamente después de expulsar la porción de masa m. En la parte inferior, las velocidades finales en el instante nτ, o las velocidades iniciales $v_{n+1}^0$, al comienzo del siguiente pulso, n=0,1,2,3...

u=9.4; %velocidad del fluido relativa al dispositivo
g=0.38; %aceleración de la gravedad efectiva
f=1/3; %cociente masas m/M
tau=10.85;  %intervalo entre dos pulsos consecutivos
gamma=0.5; %rozamiento
v0=f*u;
func=@(t) (v0+g/gamma)*exp(-gamma*t)-g/gamma;
hold on
fplot(func,[0,tau],'color','r')
plot(tau,func(tau),'o','markersize',3,'markeredgecolor','b','markerfacecolor','b') 
text(tau,func(tau), sprintf('  %1.3f',func(tau)))
plot(0,v0,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r') 
text(0,v0, sprintf('  %1.3f',v0))
for i=1:5
     v=((v0+g/gamma)*exp(-gamma*tau)-g/gamma)/(1+f)+f*u;
     line([i*tau,i*tau],[v,func(i*tau)],'lineStyle','--', 'color','k')
    func=@(t) (v+g/gamma)*exp(-gamma*(t-i*tau))-g/gamma;
    fplot(func,[i*tau,(i+1)*tau], 'color','r')
    plot(i*tau,v,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r') 
    text(i*tau,v, sprintf('  %1.3f',v))
    plot((i+1)*tau,func((i+1)*tau),'o','markersize',3,'markeredgecolor',
'b','markerfacecolor','b') 
    text((i+1)*tau,func((i+1)*tau), sprintf('  %1.3f',func((i+1)*tau)))
    v0=v;
end
hold off
grid on
xlabel('t')
ylabel('v')
title('Velocidad')

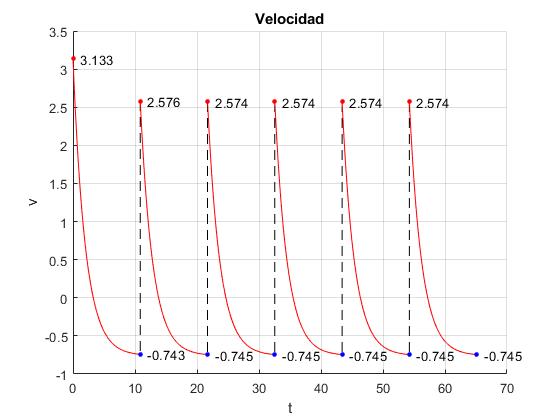
En la figura, se proporcionan los datos de la altura del dispositivo en el instante nτ. En un instante comprendido entre 0 y τ regresa al origen.

u=9.4; %velocidad del fluido relativa al dispositivo
g=0.38; %aceleración de la gravedad efectiva
f=1/3; %cociente masas m/M
tau=10.85;  %intervalo entre dos pulsos consecutivos
gamma=0.5; %rozamiento
v0=f*u;
func=@(t) (v0+g/gamma)*(1-exp(-gamma*t))/gamma-g*t/gamma;
hold on
fplot(func,[0,tau],'color','r')
plot(0,0,'o','markersize',3,'markeredgecolor','b','markerfacecolor','b') 
h0=(v0+g/gamma)*(1-exp(-gamma*tau))/gamma-g*tau/gamma;
for i=1:4
    plot(i*tau,h0,'o','markersize',3,'markeredgecolor','b','markerfacecolor','b') 
    text(i*tau,h0, sprintf('  %1.3f',h0))
     v=((v0+g/gamma)*exp(-gamma*tau)-g/gamma)/(1+f)+f*u;
    func=@(t) h0+(v+g/gamma)*(1-exp(-gamma*(t-i*tau)))/gamma-g*(t-i*tau)/gamma;
    fplot(func,[i*tau,(i+1)*tau], 'color','r')
    h0=h0+(v+g/gamma)*(1-exp(-gamma*tau))/gamma-g*tau/gamma;
    v0=v;
end
hold off
grid on
xlabel('t')
ylabel('h')
title('Altura')

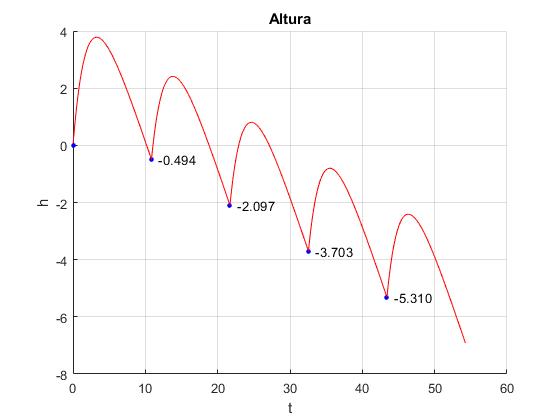
Cuando el rozamiento γ es muy pequeño, obtenemos las figuras del ejemplo al principio de esta página

Para este caso, resulta muy complicado obtener las expresiones de v_n y h_n en función de n (número de pulsos). Véase el segundo artículo citado en las referencias

Ejemplo 2

Consideremos uno de los ejemplos que se describen en el segundo artículo mencionado en las referencias

• El cociente f=0.35 entre las masas m (de fluido expulsado) y M (del dispositivo)

• El intervalo de tiempo τ=0.0208 s entre dos pulsos consecutivos

• La velocidad u=0.085 m/s de la porción de masa m de fluido expulsada, relativa al dispositivo

• La aceleración de la gravedad efectiva g de un cuerpo cuya densidad es 3% mayor que la del agua

${\displaystyle g=\left(1-\frac{{\rho }_f}{{\rho }_s}\right)g_0=\left(1-\frac{1}{1.03}\right)9.8=0.285{\text{m/s}}^{\text{2}}}$

• Sabiendo que la viscosidad del agua es η=1.58·10^-3 kg/(m·s), y que el radio del dispositivo r=0.23 mm, la constante γ=k/m=130.5 s^-1 de la fuerza de rozamiento proporcional a la velocidad

Representamos la altura del dispositivo en función del tiempo

u=0.085; %velocidad del fluido relativa al dispositivo
g=0.285; %aceleración de la gravedad efectiva
f=0.35; %cociente masas m/M
tau=0.0208;  %intervalo entre dos pulsos consecutivos
gamma=130.5; %rozamiento
v0=f*u;
func=@(t) (v0+g/gamma)*(1-exp(-gamma*t))/gamma-g*t/gamma;
hold on
fplot(func,[0,tau],'color','r')
plot(0,0,'o','markersize',3,'markeredgecolor','b','markerfacecolor','b') 
h0=(v0+g/gamma)*(1-exp(-gamma*tau))/gamma-g*tau/gamma;
for i=1:8
    plot(i*tau,h0,'o','markersize',3,'markeredgecolor','b','markerfacecolor','b') 
    v=((v0+g/gamma)*exp(-gamma*tau)-g/gamma)/(1+f)+f*u;
    func=@(t) h0+(v+g/gamma)*(1-exp(-gamma*(t-i*tau)))/gamma-g*(t-i*tau)/gamma;
    fplot(func,[i*tau,(i+1)*tau], 'color','r')
    h0=h0+(v+g/gamma)*(1-exp(-gamma*tau))/gamma-g*tau/gamma;
    v0=v;
end
hold off
grid on
xlabel('t')
ylabel('h')
title('Altura')

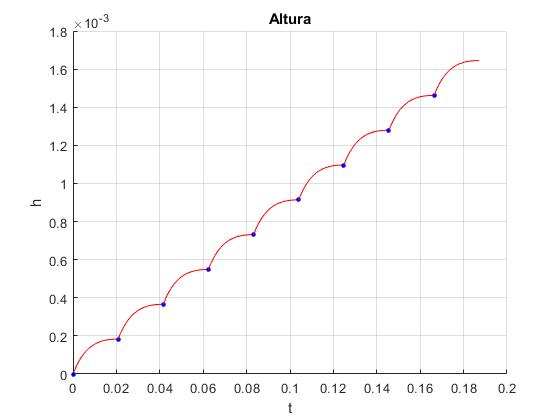
Representamos la velocidad del dispositivo en función del tiempo

u=0.085; %velocidad del fluido relativa al dispositivo
g=0.285; %aceleración de la gravedad efectiva
f=0.35; %cociente masas m/M
tau=0.0208;  %intervalo entre dos pulsos consecutivos
gamma=130.5; %rozamiento
v0=f*u;
func=@(t) (v0+g/gamma)*exp(-gamma*t)-g/gamma;
hold on
fplot(func,[0,tau],'color','r')
plot(tau,func(tau),'o','markersize',3,'markeredgecolor','b','markerfacecolor','b') 
plot(0,v0,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r') 
for i=1:8
     v=((v0+g/gamma)*exp(-gamma*tau)-g/gamma)/(1+f)+f*u;
     line([i*tau,i*tau],[v,func(i*tau)],'lineStyle','--', 'color','k')
    func=@(t) (v+g/gamma)*exp(-gamma*(t-i*tau))-g/gamma;
    fplot(func,[i*tau,(i+1)*tau], 'color','r')
    plot(i*tau,v,'o','markersize',3,'markeredgecolor','r','markerfacecolor','r') 
    plot((i+1)*tau,func((i+1)*tau),'o','markersize',3,'markeredgecolor',
'b','markerfacecolor','b') 
    v0=v;
end
hold off
grid on
xlabel('t')
ylabel('v')
title('Velocidad')

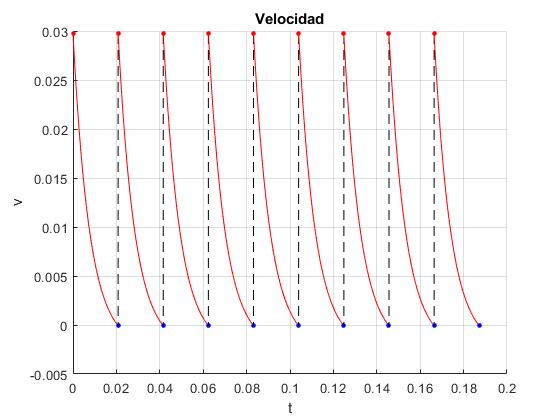
Representamos el número de Reynolds, Re en función del tiempo

u=0.085; %velocidad del fluido relativa al dispositivo
g=0.285; %aceleración de la gravedad efectiva
f=0.35; %cociente masas m/M
tau=0.0208;  %intervalo entre dos pulsos consecutivos
gamma=130.5; %rozamiento
v0=f*u;
k=1000*2*0.23e-3/1.58e-3; %número de Reynolds proporcional a v
func=@(t) k*((v0+g/gamma)*exp(-gamma*t)-g/gamma);
hold on
fplot(func,[0,tau],'color','r')
for i=1:8
     v=((v0+g/gamma)*exp(-gamma*tau)-g/gamma)/(1+f)+f*u;
     line([i*tau,i*tau],[k*v,func(i*tau)],'lineStyle','--', 'color','k')
    func=@(t) k*((v+g/gamma)*exp(-gamma*(t-i*tau))-g/gamma);
    fplot(func,[i*tau,(i+1)*tau], 'color','r')
    v0=v;
end
hold off
grid on
xlabel('t')
ylabel('Re')
title('Número de Reynolds')

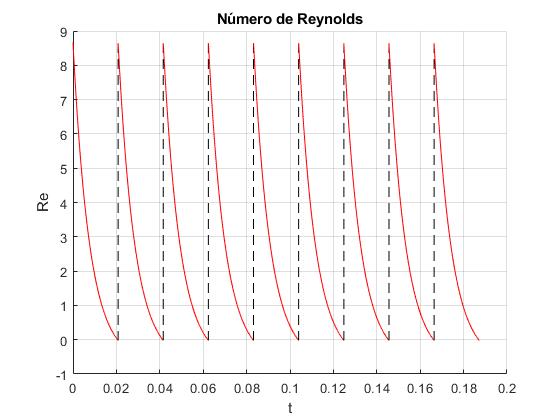
La mayor parte del tiempo el número de Reynolds Re>1. La descripción del movimiento, fuerza de rozamiento proporcional a la velocidad, es más realista cuando Re<1

Referencias

Tiberius O Cheche. Pulsejet engine dynamics in vertical motion using momentum conservation. Eur. J. Phys. 38 (2017) 025001

Mircea Dolineanu, Tiberius O. Cheche. Dynamics of the pulsejet engine in vertical motion with linear drag. Romanian Reports in Physics 71, 903, (2019)