Un cohete de empuje constante

En la página titulada Formulación discreta de las ecuaciones del movimiento de un cohete aplicamos la conservación del momento lineal a un cohete que dispara una porción de combustible de masa m con velocidad u constante relativa al cohete

Consideremos un cohete de masa inicial m que lleva una velocidad v respecto a un Sistema de Referencia Inercial (por ejemplo, la Tierra).

En el instante t+Δt, una masa Δμ se expulsa con una velocidad constante –u relativa al cohete, como consecuencia la masa restante (m-Δμ) del cohete se incrementa en v+Δv.

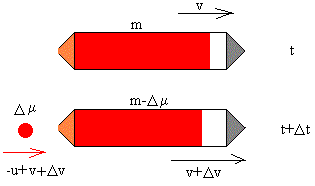
En el instante t el cohete de masa m lleva una velocidad v. Su momento lineal es

p(t)=mv

En el instante t+Δt

El cohete tiene una masa m-Δμ, su velocidad es v+Δv.
La masa expulsada Δμ lleva una velocidad –u respecto del cohete o una velocidad –u+v+Δv, respecto de Tierra

El momento lineal en este instante es

p(t+Δt)=(m-Δμ)(v+Δv)+ Δμ(–u+v+Δv)

Si el cohete está en el espacio exterior, el sistema formado por el cohete y el combustible que expulsa es aislado, el momento lineal p permanece constante. La ecuación del movimiento del cohete es

Δp=p(t+Δt)- p(t)=m·Δv-u·Δμ=0

En el límite cuando Δt→0

$m \frac{d v}{d t} - u \frac{d μ}{d t} = 0$

La masa M del sistema formado por el cohete m y el combustible expulsado μ es constante M=μ+m, por lo que dμ+dm=0. La masa del cohete disminuye en dm y aumenta la masa del combustible expulsado en la misma cantidad.

$m \frac{d v}{d t} + u \frac{d m}{d t} = 0$

Suponemos que la cantidad de combustible quemado en la unidad de tiempo, D, es constante, D=-dm/dt. La masa m del cohete en el instante t valdrá m=m₀-D·t. Donde m₀ es la suma de la carga útil más el combustible inicial, y D·t es el combustible quemado al cabo de un cierto tiempo t.

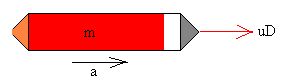
Interpretamos la ecuación del movimiento, afirmando que el cohete se comporta como una partícula de masa variable m que se mueve bajo la acción de una fuerza de empuje constante u·D.

$m \frac{d v}{d t} = u \cdot D$

Velocidad

Eliminando dt de la ecuación diferencial m·dv/dt+u·dm/dt=0, despejando dv

$d v = - u \frac{d m}{m} \int_{v_{0}}^{v} d v = - u \int_{m_{0}}^{m} \frac{d m}{m}$

cuya integración entre los instantes 0 y t conduce a la siguiente expresión

$v = v_{0} + u \cdot \ln \frac{m_{0}}{m} v = v_{0} + u \cdot \ln \frac{m_{0}}{m_{0} - D t}$

Si el cohete parte del reposo v₀=0. La velocidad v del cohete se hace igual a la de los gases expulsados u cuando m₀/m=e. Es decir, cuando m/m₀≈37%

Momento lineal y energía cinética

$\begin{array}{l} p = m u \ln (\frac{m_{0}}{m}) \\ E_{k} = \frac{1}{2} m u^{2} {(\ln (\frac{m_{0}}{m}))}^{2} \end{array}$

Representamos la velocidad, v, el momento lineal p y la energía cinética E_k tomando la masa inicial m₀=1 y la velocidad constante de salida de los gases respecto del cohete, u=1

m0=1; %masa inici
u=1; %velocidad de los gases
hold on
fplot(@(m) u*log(m0./m), [0,1])
f=@(m) (m*u).*log(m0./m);
fplot(f, [0,1])
line([1/exp(1),1/exp(1)],[0,f(1/exp(1))],'lineStyle','--')
g=@(m) (m*u^2).*log(m0./m).^2/2;
fplot(g, [0,1])
line([1/exp(2),1/exp(2)],[0,g(1/exp(2))],'lineStyle','--')
hold off
set(gca, 'XDir','reverse')
xlabel('m')
ylabel('v,p,E_k')
ylim([0,1])
legend('v','p','E_k','Location','best')
grid on
title('Cohete')

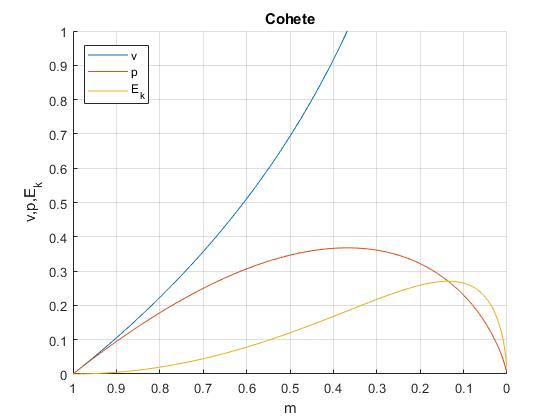
La velocidad v crece, a medida que se va agotando el combustible. El momento lineal y la energía cinética presentan un máximo para valores del cociente m/m₀ que vamos a calcular

$\begin{array}{l} \frac{d p}{d m} = \ln (\frac{m_{0}}{m}) - 1 = 0 \\ \frac{m}{m_{0}} = \frac{1}{e} \approx 0.37 \\ \frac{d E_{k}}{d m} = \frac{1}{2} u^{2} {{(\ln (\frac{m_{0}}{m}))}^{2} - 2 \ln (\frac{m_{0}}{m})} = 0 \\ \ln (\frac{m_{0}}{m}) = 2 \\ \frac{m}{m_{0}} = \frac{1}{e^{2}} \approx 0.13 \end{array}$

El momento lineal es máximo cuando la velocidad v del cohete se hace igual a la de los gases expulsados u, es decir, cuando m/m₀≈37%

Si un cohete se utiliza para desviar un asteroide potencialmente peligroso, su momento lineal (no la velocidad) deberá ser el máximo posible

La energía cinética es máxima cuando la velocidad v del cohete se hace igual 2u, es decir, cuando m/m₀≈13%

Sin embargo, cuando el cohete se utiliza para penetrar en la superficie del cuerpo celeste su energía deberá ser máxima

Posición

Integramos la expresión de la velocidad para calcular la posición x del cohete en el instante t

$x - x_{0} = \int_{0}^{t} v \cdot d t$

Sabiendo el resultado de la integral

$\int \ln z \cdot d z = z \cdot \ln z - z$

>> syms x;
>> int('log(x)',x)
ans =x*(log(x) - 1)

Obtenemos la expresión

$x = x_{0} + v_{0} t + u t \ln m_{0} + \frac{u}{D} [(m_{0} - D t) \ln (m_{0} - D t) + D t - m_{0} \ln m_{0}]$

Cuando se agota el combustible, el cohete se mueve con velocidad constate.

Momento lineal

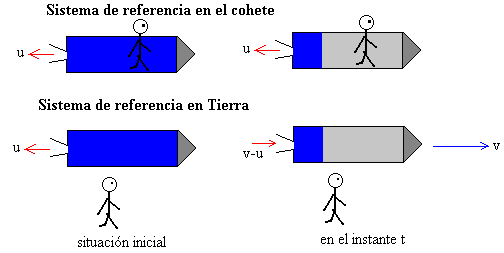
Un cohete con una masa inicial m₀ empieza a expulsar los gases con velocidad u relativa al cohete y por consiguiente, comienza a moverse en el espacio exterior. Al cabo de un cierto tiempo, alcanza una velocidad v, expulsando los gases con una velocidad u relativa al cohete o con una velocidad v-u relativa al observador terrestre.

Si el cohete parte del reposo v₀=0, la velocidad de los gases respecto del observador terrestre v-u no es constante. Al principio tiene sentido contrario al movimiento del cohete v-u<0, pero al cabo de un cierto tiempo t la velocidad de los gases v-u>0 es del mismo sentido que la del cohete.

$u \cdot \ln \frac{m_{0}}{m_{0} - D t} - u > 0 \frac{m_{0}}{m_{0} - D t} > e$

$t > 0.632 \frac{m_{0}}{D}$

En el instante t=0.632m₀/D los gases expulsados están en reposo respecto del observador terrestre.

El momento lineal del cohete en el instante t, es

$m v = (m_{0} - D t) \cdot u \cdot \ln \frac{m_{0}}{m_{0} - D t}$

El momento lineal de los gases expulsados entre el instante t=0, y el instante t, es

$\int_{0}^{t} d m (v - u) = D \int_{0}^{t} (u \ln \frac{m_{0}}{m_{0} - D t} - u) d t = - u (m_{0} - D t) \ln \frac{m_{0}}{m_{0} - D t}$

Como el cohete y los gases forman un sistema aislado el momento lineal del cohete es igual y de sentido contrario al de los gases expulsados desde el instante inicial t=0, al instante t. Como la velocidad de los gases respecto del observador terrestre no es constante es necesario calcular una integral para obtener el momento total de los gases expulsados hasta el instante t y comprobar de este modo, que se cumple el principio de conservación del momento lineal, principio en el que nos hemos basado por otra parte, para obtener la ecuación del movimiento del cohete.

Energías

La energía cinética del cohete en el instante t es

$E_{c} = \frac{1}{2} m v^{2} = \frac{1}{2} (m_{0} - D t) v^{2}$

La energía cinética de los gases expulsados desde el instante t=0, al instante t es

$\begin{array}{l} E_{g} = \int_{0}^{t} \frac{1}{2} d m {(v - u)}^{2} = \frac{1}{2} D t \cdot u^{2} - \frac{1}{2} (m_{0} - D t) {(u \ln \frac{m_{0}}{m_{0} - D t})}^{2} \\ E_{g} = \frac{1}{2} D t \cdot u^{2} - \frac{1}{2} (m_{0} - D t) v^{2} \end{array}$

Para llegar a esta expresión, es necesario conocer el resultado de las siguientes las integrales:

$\begin{array}{l} \int \ln z \cdot d z = z \cdot \ln z - z \\ \int \ln^{2} z \cdot d z = z \cdot \ln^{2} z - 2 z \ln z + 2 z \end{array}$

>> syms x;
>> int('log(x)^2',x)
ans =x*(log(x)^2 - 2*log(x) + 2)

La energía cinética total del sistema aislado formado por el cohete y los gases en el instante t es

$E_{c} + E_{g} = \frac{1}{2} D t \cdot u^{2}$

El rendimiento del cohete en el instante t es el cociente entre la energía cinética del cohete y la energía cinética total (cohete más los gases expulsados).

Ejemplo

Combustible total en el cohete 9000 kg
Carga útil que transporta 800 kg
Combustible quemado por segundo D=1000 kg/s
La velocidad constante de salida de los gases es u=2000 m/s respecto del cohete
La masa del recipiente que contiene el combustible es el 5% de la masa del combustible

Masa total del cohete=carga útil+combustible+masa del recipiente

m₀=800+9000+0.05·9000=10250 kg

Tiempo que tarda en agotarse el combustible

Como hay 9000 kg de combustible que se queman a razón de 1000 kg/s, el combustible se agota en 9 s.
Velocidad máxima alcanzada por el cohete

$v = u \ln \frac{m_{0}}{m_{0} - D t} = 2000 \cdot \ln (\frac{10250}{10250 - 9000}) = 4208 m/s$

Distancia recorrida hasta que se agota el combustible

$\begin{array}{l} x = u t \ln m_{0} + \frac{u}{D} [(m_{0} - D t) \ln (m_{0} - D t) + D t - m_{0} \ln m_{0}] \\ x = 2000 \cdot 9 \cdot \ln 10250 + \frac{2000}{1000} [1250 \ln 1250 + 9000 - 10250 \ln 10250] = 12740 m \end{array}$

Energías

La energía total proporcionada por el combustible es

$E_{i} = \frac{1}{2} D t \cdot u^{2} = \frac{1}{2} 9000 \cdot 2000^{2} J$

La energía cinética del cohete cuando se ha agotado el combustible es

$E_{k} = \frac{1}{2} (10250 - 9000) \cdot 4208^{2} J$

El rendimiento es el cociente entre E_k/E_i=61.5%

u=2000; %velocidad de escape de los gases (respecto al cohete)
combustible=9000; %combustible
carga=800;  %carga útil
m0=carga+1.05*combustible; %masa total
D=1000; %kg de combustible quemado por segundo
tf=combustible/D; %tiempo hasta que se agota el combustible

figure
t=0:0.05:tf;
v=u*log(m0./(m0-D*t));
plot(t,v)
grid on
xlabel('t(s)')
ylabel('v(m/s)')
title('Velocidad')

figure
x=u*t*log(m0)+u*((m0-D*t).*log(m0-D*t)+D*t-m0*log(m0))/D;
plot(t,x)
grid on
xlabel('t(s)')
ylabel('x(m)')
title('Posición')
fprintf('Velocidad final %4.1f, posición final %5.1f\n',v(end),x(end));

Velocidad final 4208.3, posición final 12739.7

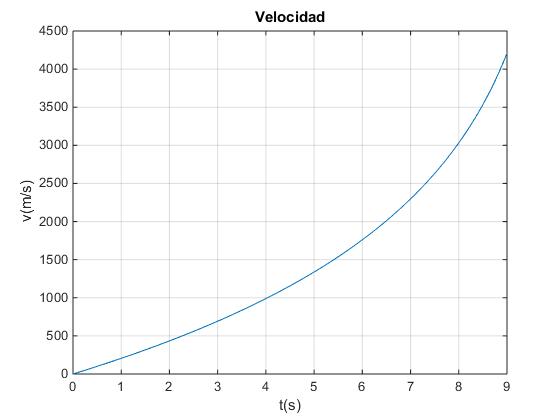
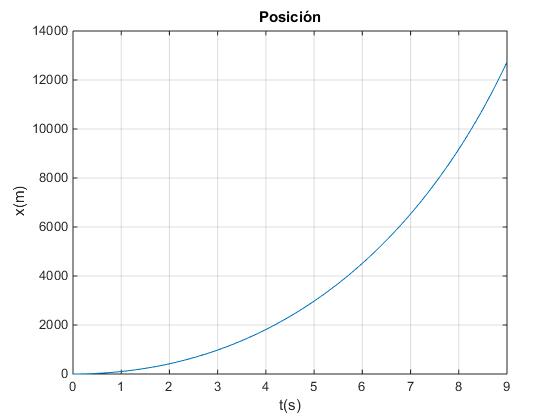
Velocidad final 4208.3, posición final 12739.7

Actividades

Se introduce.

El combustible c, en el control titulado Combustible total en el cohete
La carga útil que transporta, en el control titulado Carga útil que transporta
La cantidad D de combustible que se quema por segundo, en el control titulado Combustible quemado por seg.
La velocidad constante de salida de los gases se ha fijado en u=2000 m/s respecto del cohete
La masa del recipiente que contiene el combustible se ha fijado en el 5% de la masa del combustible

Se pulsa el botón titulado Nuevo.

El cohete parte con velocidad inicial cero v₀=0 desde el origen x₀=0.

La masa inicial m₀ es la suma de la carga útil, más el combustible y más la masa del recipiente cilíndrico que será proporcional a la masa del combustible que contiene

masa inicial m₀ =carga útil +(1+r) ·combustible.

donde r es del orden del 5% ó 0.05

El tiempo t_máx que tarda en agotarse el combustible es igual al cociente entre la masa de combustible c y la cantidad D que se quema por segundo

t_máx=c/D

Cuando se agota el combustible c, el cohete describe un movimiento rectilíneo y uniforme, ya que no actúan fuerzas sobre el mismo.

$v = u \ln \frac{m_{0}}{m_{0} - c}$

En la cola del cohete se dibuja una flecha que indica la fuerza de empuje. Como la velocidad de los gases es constante (en el Sistema de Referencia en el cohete) el empuje es constante.

Comprobamos que el cohete alcanza el mismo valor de la velocidad máxima, independientemente de la cantidad D de combustible quemado en la unidad de tiempo. Mantener constantes la cantidad de de combustible c, la carga útil y variar la cantidad de combustible quemado por segundo. Anotar en una tabla la velocidades finales v_máx, una vez agotado todo el combustible, el tiempo empleado en alcanzar la velocidad máxima t_máx, y el desplazamiento del cohete x hasta este instante.

Se muestra el balance energético del cohete. Un círculo muestra la energía inicial del combustible en el cohete y cómo esta energía se va transformando en energía cinética de los gases expulsados y en energía cinética del cohete. Al agotarse todo el combustible, una parte de la energía inicial del combustible se ha transformado en energía cinética del cohete.

Combustible total en el cohete (kg)<20000
Combustible quemado por seg (kg/s) <2000
Carga útil < 2000
Energía

Referencias

Philip Blanco. Maximum Momentum and Kinetic Energy of a Rocket. The Physics Teacher, Vol. 58, November 2020, pp. 534-535