En las páginas previas, se ha supuesto que la masa del cohete decrece linealmente con el tiempo hasta el instante t_f en el que se agota el combustible, m=m₀-D·t, donde D=-dm/dt cantidad de combustible quemado en la unidad de tiempo. El empuje constante es el producto uD, siendo u la velocidad de salida de los gases respecto del cohete. La masa final del cohete es m_f=m₀-D·t_f

En esta página, supondremos que la masa disminuye exponencialmente con el tiempo, m=m₀exp(-t/τ), hasta el instante t_f en el que se agota el combustible. La masa final del cohete será m_f=m₀exp(-t_f/τ). El combustible gastado es la diferencia m₀-m_f

Sin rozamiento

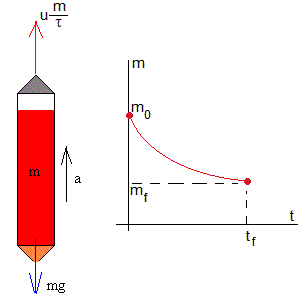
Hemos deducido la ecuación de un cohete que se mueve verticalmente sin rozamiento

${\displaystyle -mg=m\frac{dv}{dt}+u\frac{dm}{dt}}$

Un cohete puede considerarse una partícula de masa variable m sometida a la acción de dos fuerzas de la misma dirección y sentido contrario:

• El peso, mg
• El empuje de los gases

La ecuación del movimiento para t<t_f es

${\displaystyle \begin{array}{l}m=m_0\exp \left(-\frac{t}{\tau }\right),\frac{dm}{dt}=-\frac{m_0}{\tau }\exp \left(-\frac{t}{\tau }\right)=-\frac{m}{\tau }\\ -mg=m\frac{dv}{dt}-u\frac{m}{\tau }\\ \frac{dv}{dt}=\frac{u}{\tau }-g\end{array}}$

La aceleración es constante. Para que el cohete ascienda partiendo del reposo, u/τ>g

La velocidad y altura del cohete serán

${\displaystyle \begin{array}{l}v=v_0+\left(\frac{u}{\tau }-g\right)t\\ x=v_{0}t+\frac{1}{2}\left(\frac{u}{\tau }-g\right)t^2\end{array}}$

A continuación, estudiaremos dos casos de fuerza de rozamiento F_r:

• Fuerza de rozamiento proporcional a la velocidad
• Fuerza de rozamiento proporcional al cuadrado de la velocidad

Fuerza de rozamiento proporcional a la velocidad

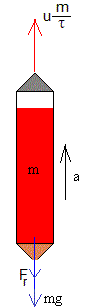
En este caso F_r=bv. La ecuación del movimiemto de escribe

${\displaystyle \begin{array}{l}-mg-bv=m\frac{dv}{dt}+u\frac{dm}{dt}\\ m\frac{dv}{dt}=m\frac{u}{\tau }-mg-bv\\ \frac{dv}{dt}+\frac{b}{m}v=\frac{u}{\tau }-g\end{array}}$

Hacemos el cambio de variable

${\displaystyle \begin{array}{l}\xi =\frac{b\tau }{m}=\frac{b\tau }{m_0}\exp \left(\frac{t}{\tau }\right)\\ \frac{dv}{dt}=\frac{dv}{d\xi }\frac{d\xi }{dt}=\frac{dv}{d\xi }\frac{b}{m}=\frac{dv}{d\xi }\frac{\xi }{\tau }\end{array}}$

Sustituyendo en la ecuación diferencial

${\displaystyle \begin{array}{l}\frac{dv}{d\xi }\frac{\xi }{\tau }+\frac{\xi }{\tau }v=\frac{u}{\tau }-g\\ \frac{dv}{d\xi }+v=\left(\frac{u}{\tau }-g\right)\frac{\tau }{\xi }\end{array}}$

Tenemos una ecuación del tipo

${\displaystyle \frac{dv}{d\xi }+P(\xi )v=Q(\xi ),\{\begin{array}{l}P(\xi )=1\\ Q(\xi )=\left(\frac{u}{\tau }-g\right)\frac{\tau }{\xi }\end{array}}$

cuya solución es

${\displaystyle v(\xi )=\exp \left(-{\displaystyle \int P(\xi )d\xi }\right)\left\{c+{\displaystyle \int Q(\xi )\exp \left({\displaystyle \int P(\xi )d\xi }\right)d\xi }\right\}}$

donde c es una constante que determina la condición inicial, en el instante t=0, parte con velocidad v₀.

${\displaystyle \begin{array}{l}{\displaystyle \int P(\xi )d\xi }=\xi \\ {\displaystyle \int \left(\frac{u}{\tau }-g\right)\frac{\tau }{\xi }\exp \left(\xi \right)d\xi }=\left(u-g\tau \right){\displaystyle \int \frac{\exp \left(\xi \right)}{\xi }d\xi }\\ v(\xi )=\exp \left(-\xi \right)\left\{c+\left(u-g\tau \right){\displaystyle \int \frac{\exp \left(\xi \right)}{\xi }d\xi }\right\}\end{array}}$

La constante c se determina a partir de las condiciones iniciales, t=0, v=v₀, ξ₀=bτ/m₀

${\displaystyle \begin{array}{l}{v}_0=\exp \left(-{\xi }_0\right)\left\{c+\left(u-g\tau \right)f\left({\xi }_0\right)\right\}\\ c=v_0\exp \left({\xi }_0\right)-\left(u-g\tau \right)f\left({\xi }_0\right)\end{array}}$

La expresión de la velocidad v en función del tiempo t es

${\displaystyle \begin{array}{l}v(\xi )=\exp \left(-\xi \right)\left\{v_0\exp \left({\xi }_0\right)+\left(u-g\tau \right)\left(f(\xi )-f\left({\xi }_0\right)\right)\right\}\\ v(\xi )=\exp \left(-\xi \right)\left\{v_0\exp \left({\xi }_0\right)+\left(u-g\tau \right)\left({\displaystyle \underset{-\infty }{\overset{\xi }{\int }}\frac{e^{\xi }}{\xi }}d\xi -{\displaystyle \underset{-\infty }{\overset{{\xi }_0}{\int }}\frac{e^{\xi }}{\xi }}d\xi \right)\right\}\\ v(\xi )=\exp \left(-\xi \right)\left\{v_0\exp \left({\xi }_0\right)+\left(u-g\tau \right)\left(\text{ei(}\xi )-e\text{i(}{\xi }_0)\right)\right\}\end{array}}$

Donde ei(ξ) se denomina función integral exponencial

Ejemplo

Sea un cohete

• Masa inicial, m₀=1000 kg
• Agota el compustible en el instante, t_f=42.1 s
• Velocidad de salida de los gases, respecto del cohete, u=400 m/s
• Parámetro, τ=35 s
• Velocidad inicial, v₀=30 m/s

Representamos

• La velocidad del cohete v en función del tiempo, cuando no se tiene en cuenta el rozamiento, en color negro
• Cuando se tiene en cuenta el rozamiento, para dos valores del parametro b=10 kg/s

u=400; %velocidad de salida de los gases
v0=30; %velocidad inicial
tau=35; %parámetro
tf=42.1; %agota el combustible
m0=1000; %masa inicial
b=10;
hold on
%sin rozamiento
v=@(t) v0+(u/tau-9.8)*t;
fplot(v,[0,tf], 'color','k')
%solución analítica
v=@(t) exp(-b*tau*exp(t/tau)/m0).*(v0*exp(b*tau/m0)+(u-9.8*tau)*
(ei(b*tau*exp(t/tau)/m0)-ei(b*tau/m0)));
fplot(v,[0,tf])
%solución numérica
f=@(t,x) [x(2); u/tau-9.8-b*x(2)*exp(t/tau)/m0];
[t,x]=ode45(f,[0,tf],[0,v0]);
plot(t,x(:,2))
hold off
grid on
xlabel('t (s)')
ylabel('v (m/s)')
title('Velocidad')

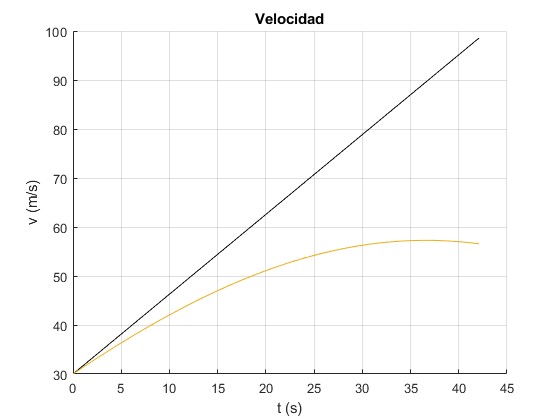
Observamos que la solución numérica de la ecuación diferencial del movimiento, utilizando el procedimiento ode45 de MATLAB, coincide con la analítica

${\displaystyle \frac{d^{2}x}{d{t}^2}+\frac{b}{m_0}\frac{dx}{dt}\exp \left(\frac{t}{\tau }\right)=\frac{u}{\tau }-g}$

Las condiciones iniciales son, en el instante t=0, x=0, dx/dt=v₀

Fuerza de rozamiento proporcional al cuadrado de la velocidad

En este caso F_r=bv². La ecuación del movimiemto de escribe

${\displaystyle \frac{dv}{dt}+\frac{b}{m}{v}^2=\frac{u}{\tau }-g}$

Es una ecuación del tipo

${\displaystyle \frac{dv}{dt}+a_2{v}^2-a_0=\mathrm{0,}\{\begin{array}{l}{a}_2(t)=\frac{b}{m_0}\exp \left(\frac{t}{\tau }\right)\\ a_0=\frac{u}{\tau }-g\end{array}}$

que es complicada de resolver

Definimos una nueva variable χ, tal que

${\displaystyle v=\frac{\frac{d\chi }{dt}}{a_2\chi }}$

Derivamos respecto del tiempo

${\displaystyle \frac{dv}{dt}=\frac{\frac{d^2\chi }{d{t}^2}{a}_2\chi -\left(\frac{d{a}_2}{dt}\chi +a_2\frac{d\chi }{dt}\right)\frac{d\chi }{dt}}{a_2^2{\chi }^2}=\frac{\frac{d^2\chi }{d{t}^2}}{a_2\chi }-\frac{\frac{d{a}_2}{dt}\frac{d\chi }{dt}}{a_2^2\chi }-\frac{{\left(\frac{d\chi }{dt}\right)}^2}{a_2{\chi }^2}}$

Introduciendo v y dv/dt en la ecuación diferencial, obtenemos

${\displaystyle a_2\frac{d^2\chi }{d{t}^2}-\frac{d{a}_2}{dt}\frac{d\chi }{dt}-a_0{a}_2^2\chi =0}$

Definimos una nueva variable ξ

${\displaystyle \xi =2\tau \sqrt{\frac{b{a}_0}{m}}=2\tau \sqrt{\frac{b{a}_0}{m_0}\exp \left(\frac{t}{\tau }\right)}}$

Cambiamos la variable t por ξ

${\displaystyle \begin{array}{l}\frac{d\chi }{dt}=\frac{d\chi }{d\xi }\frac{d\xi }{dt}=\frac{\xi }{2\tau }\frac{d\chi }{d\xi }\\ \frac{d^2\chi }{d{t}^2}=\frac{d}{dt}\left(\frac{d\chi }{dt}\right)=\frac{d}{d\xi }\left(\frac{d\chi }{dt}\right)\frac{d\xi }{dt}=\frac{d}{d\xi }\left(\frac{\xi }{2\tau }\frac{d\chi }{d\xi }\right)\frac{d\xi }{dt}=\left(\frac{1}{2\tau }\frac{d\chi }{d\xi }+\frac{\xi }{2\tau }\frac{d^2\chi }{d{\xi }^2}\right)\frac{\xi }{2\tau }=\frac{1}{4{\tau }^2}\left(\xi \frac{d\chi }{d\xi }+{\xi }^2\frac{d^2\chi }{d{\xi }^2}\right)\\ \frac{d{a}_2}{dt}=\frac{a_2}{\tau }\\ a_0{a}_2=\frac{{\xi }^2}{4{\tau }^2}\end{array}}$

Introducimos, a₀a₂, da₂/dt, dχ/dt, d²χ/dt² en la ecuación diferencial, que se transforma en

${\displaystyle \begin{array}{l}\frac{d^2\chi }{d{t}^2}-\frac{1}{\tau }\frac{d\chi }{dt}-a_0{a}_2\chi =0\\ \frac{1}{4{\tau }^2}\left(\xi \frac{d\chi }{d\xi }+{\xi }^2\frac{d^2\chi }{d{\xi }^2}\right)-\frac{1}{\tau }\frac{\xi }{2\tau }\frac{d\chi }{d\xi }-\frac{{\xi }^2}{4{\tau }^2}\chi =0\\ \xi \frac{d^2\chi }{d{\xi }^2}-\frac{d\chi }{d\xi }-\xi \chi =0\end{array}}$

Haciendo el cambio

${\displaystyle \begin{array}{l}\chi =\xi ·\phi (\xi )\\ \frac{d\chi }{d\xi }=\phi +\xi \frac{d\phi }{d\xi }\\ \frac{d^2\chi }{d{\xi }^2}=\frac{d\phi }{d\xi }+\frac{d\phi }{d\xi }+\xi \frac{d^2\phi }{d{\xi }^2}=2\frac{d\phi }{d\xi }+\xi \frac{d^2\phi }{d{\xi }^2}\end{array}}$

Sustituyendo en la ecuación diferencial

${\displaystyle \begin{array}{l}\xi \left(2\frac{d\phi }{d\xi }+\xi \frac{d^2\phi }{d{\xi }^2}\right)-\left(\phi +\xi \frac{d\phi }{d\xi }\right)-{\xi }^2\phi =0\\ {\xi }^2\frac{d^2\phi }{d{\xi }^2}+\xi \frac{d\phi }{d\xi }-\left({\xi }^2+1\right)\phi =0\end{array}}$

Obtenemos una ecuación de Bessel, cuya solución es

${\displaystyle \phi (\xi )=c_1{I}_1(\xi )+c_2{K}_1(\xi )}$

La expresión de la velocidad v(ξ) es

${\displaystyle \begin{array}{l}v=\frac{\frac{d\chi }{dt}}{a_2\chi }=\frac{\frac{\xi }{2\tau }\left(\phi +\xi \frac{d\phi }{d\xi }\right)}{\frac{{\xi }^2}{4{\tau }^2{a}_0}\xi ·\phi (\xi )}=\frac{2\tau a_0}{{\xi }^2}\frac{c_1{I}_1(\xi )+c_2{K}_1(\xi )+\xi \left(c_1\left(I_0(\xi )-\frac{I_1(\xi )}{\xi }\right)+c_2\left(-K_0(\xi )-\frac{K_1(\xi )}{\xi }\right)\right)}{c_1{I}_1(\xi )+c_2{K}_1(\xi )}\\ v(\xi )=\frac{2\tau a_0}{\xi }\frac{\left(c{I}_0(\xi )-K_0(\xi )\right)}{\left(c{I}_1(\xi )+K_1(\xi )\right)},\xi =2\tau \sqrt{\frac{b{a}_0}{m_0}\exp \left(\frac{t}{\tau }\right)}\end{array}}$

La constante c=c₁/c₂ se determina sabiendo que en el instante t=0, m=m₀, y v=v₀.

${\displaystyle \begin{array}{l}{v}_0=\frac{2\tau a_0}{{\xi }_0}\frac{\left(c{I}_0({\xi }_0)-K_0({\xi }_0)\right)}{\left(c{I}_1({\xi }_0)+K_1({\xi }_0)\right)},{\xi }_0=2\tau \sqrt{\frac{b{a}_0}{m_0}}\\ c=\frac{2\tau a_0{K}_0({\xi }_0)+v_0{\xi }_0{K}_1({\xi }_0)}{2\tau a_0{I}_0({\xi }_0)-v_0{\xi }_0{I}_1({\xi }_0)}\end{array}}$

Ejemplo

Sea un cohete

• Masa inicial, m₀=1000 kg
• Agota el compustible en el instante, t_f=18.1 s
• Velocidad de salida de los gases, respecto del cohete, u=1200 m/s
• Parámetro, τ=25 s
• Velocidad inicial, v₀=200 m/s

Representamos

• La velocidad del cohete v en función del tiempo, cuando no se tiene en cuenta el rozamiento, en color negro
• Cuando se tiene en cuenta el rozamiento, para dos valores del parametro b=0.04 kg/m

u=1200; %velocidad de salida de los gases
v0=200; %velocidad inicial
tau=15; %parámetro
tf=18.1; %agota el combustible
m0=1000; %masa inicial
b=0.04;
hold on
%sin rozamiento
a0=u/tau-9.8;
v=@(t) v0+a0*t;
fplot(v,[0,tf], 'color','k')
%solución analítica
xi_0=2*tau*sqrt(b*a0/m0);
c=(2*tau*a0*besselk(0,xi_0)+v0*xi_0*besselk(1,xi_0))/
(2*tau*a0*besseli(0,xi_0)-v0*xi_0*besseli(1,xi_0));
v=@(t) 2*tau*a0*(c*besseli(0,2*tau*sqrt(b*a0*exp(t/tau)/m0))-
besselk(0,2*tau*sqrt(b*a0*exp(t/tau)/m0)))./(2*tau*sqrt(b*a0*exp(t/tau)/m0).*
(c*besseli(1,2*tau*sqrt(b*a0*exp(t/tau)/m0))+besselk(1,2*tau*
sqrt(b*a0*exp(t/tau)/m0))));
fplot(v,[0,tf])
%solución numérica
f=@(t,x) [x(2); u/tau-9.8-b*x(2)^2*exp(t/tau)/m0];
[t,x]=ode45(f,[0,tf],[0,v0]);
plot(t,x(:,2))
hold off
grid on
xlabel('t (s)')
ylabel('v (m/s)')
title('Velocidad')

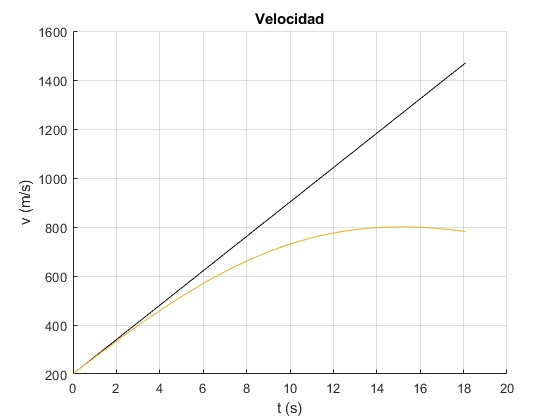
Observamos que la solución numérica de la ecuación diferencial del movimiento, utilizando el procedimiento ode45 de MATLAB, coincide con la analítica

${\displaystyle \frac{d^{2}x}{d{t}^2}+\frac{b}{m_0}{\left(\frac{dx}{dt}\right)}^2\exp \left(\frac{t}{\tau }\right)=\frac{u}{\tau }-g}$

Las condiciones iniciales son, en el instante t=0, x=0, dx/dt=v₀

Referencias

Hilário Rodrigues, Marcos Oliveira Pinho, Dirceu Portes Jr., Arnaldo José Santiago. Modelling the dynamics of bodies self-propelled by exponential mass exhaustion. Eur. J. Phys. 29 (2008) pp. 527–537