Hemos deducido la ecuación de un cohete que se mueve verticalmente sin rozamiento

${\displaystyle -mg=m\frac{dv}{dt}+u\frac{dm}{dt}}$

Supongamos que la cantidad de combustible quemado en la unidad de tiempo, D, es constante, D=-dm/dt. La masa m del cohete en el instante t valdrá m=m₀-D·t. Donde m₀ es la suma de la carga útil más el combustible inicial, y D·t es el combustible quemado al cabo de un cierto tiempo t. El combustible se agota en el instante t_f, la masa final del cohete es m_f=m₀-D·t_f

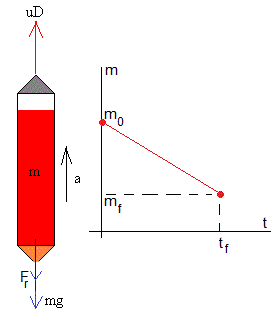
Un cohete puede considerarse una partícula de masa variable m sometida a la acción de tres fuerzas de la misma dirección:

• El peso, mg
• El empuje de los gases, uD
• La fuerza de rozamiento, F_r

La ecuación del movimiento para t<t_f es

${\displaystyle m\frac{dv}{dt}=-mg-F_r+uD,m=m_0-Dt}$

Estudiamos dos casos de fuerza de rozamiento F_r:

• Fuerza de rozamiento proporcional a la velocidad
• Fuerza de rozamiento proporcional al cuadrado de la velocidad

Fuerza de rozamiento proporcional a la velocidad

En este caso F_r=bv. La ecuación del movimiemto de escribe

${\displaystyle \frac{dv}{dt}+\frac{b}{m_0-Dt}v=-g+\frac{uD}{m_0-Dt}}$

Tenemos una ecuación del tipo

${\displaystyle \frac{dv}{dt}+P(t)v=Q(t)\{\begin{array}{l}P(t)=\frac{b}{m_0-Dt}\\ Q(t)=-g+\frac{uD}{m_0-Dt}\end{array}}$

cuya solución es

${\displaystyle v(t)=\exp \left(-{\displaystyle \int P(t)dt}\right)\left\{c+{\displaystyle \int Q(t)\exp \left({\displaystyle \int P(t)dt}\right)dt}\right\}}$

donde c es una constante que determina la condición inicial, en el instante t=0, parte del reposo v=0.

${\displaystyle \begin{array}{l}{\displaystyle \int P(t)dt}={\displaystyle \int \frac{b}{m_0-Dt}dt=-\frac{b}{D}\ln \left(m_0-Dt\right)}\\ \exp \left(-{\displaystyle \int P(t)dt}\right)=\exp \left(\frac{b}{D}\ln \left(m_0-Dt\right)\right)={\left(m_0-Dt\right)}^{\frac{b}{D}}\\ Q(t)\exp \left({\displaystyle \int P(t)dt}\right)=\left(-g+\frac{uD}{m_0-Dt}\right){\left(m_0-Dt\right)}^{-\frac{b}{D}}\\ {\displaystyle \int \left\{-g{\left(m_0-Dt\right)}^{-\frac{b}{D}}+uD{\left(m_0-Dt\right)}^{-\frac{b}{D}-1}\right\}dt}=\frac{g}{D}{\left(m_0-Dt\right)}^{-\frac{b}{D}+1}+\frac{uD}{b}{\left(m_0-Dt\right)}^{-\frac{b}{D}}\end{array}}$

La expresión de la velocidad v en función del tiempo t es

${\displaystyle v=c{\left(m_0-Dt\right)}^{\frac{b}{D}}+\frac{g}{D-b}\left(m_0-Dt\right)+\frac{uD}{b}}$

Teniendo en cuenta que para t=0, v=0

${\displaystyle c=-\frac{gb{m}_0+uD(D-b)}{b(D-b)m_0^{b/D}}}$

Altura

Integramos para calcular altura x en función del tiempo t

${\displaystyle \begin{array}{l}x(t)={\displaystyle \underset{0}{\overset{t}{\int }}v(t)·dt}=\\ \frac{uD}{b}t-\frac{g}{2D\left(D-b\right)}{\left(m_0-Dt\right)}^2-\frac{c}{D+b}{\left(m_0-Dt\right)}^{\frac{b}{D}+1}+\frac{g}{2D\left(D-b\right)}{m}_0^2+\frac{c}{D+b}{m}_0^{1+b/D}\end{array}}$

Se agota el combustible

En el instante t_f en el que se agota el combustible, la masa del cohete es m_f=m₀-D·t_f, su velocidad es v_f y su altura x_f. La ecuación del movimiento es

${\displaystyle m_f\frac{dv}{dt}=-m_{f}g-bv}$

Integrando, obtenemos la velocidad v en función del tiempo t

${\displaystyle \begin{array}{l}-{\displaystyle \underset{v_f}{\overset{v}{\int }}\frac{dv}{g+\frac{b}{m_f}v}}={\displaystyle \underset{t_f}{\overset{t}{\int }}dt}\\ v(t)=\left(\frac{m_{f}g}{b}+v_f\right)\exp \left(-\frac{b}{m_f}(t-t_f)\right)-\frac{m_{f}g}{b}\end{array}}$

Se alcanza la altura máxima en el instante t, cuando la velocidad es nula v=0

${\displaystyle \begin{array}{l}\exp \left(-\frac{b}{m_f}(t-t_f)\right)=\frac{m_{f}g}{m_{f}g+b{v}_f}\\ t=t_f+\frac{m_f}{b}\ln \left(\frac{m_{f}g+b{v}_f}{m_{f}g}\right)\end{array}}$

Integramos de nuevo, para obtener la altura x en función del tiempo t

${\displaystyle \begin{array}{l}x(t)-x_f={\displaystyle \underset{t_f}{\overset{t}{\int }}v(t)·dt}\\ x(t)=x_f+\frac{m_f}{b}\left(\frac{m_{f}g}{b}+v_f\right)\left\{1-\exp \left(-\frac{b}{m_f}(t-t_f)\right)\right\}-\frac{m_{f}g}{b}(t-t_f)\end{array}}$

Ejemplo

Sea un cohete

• Masa inicial, m₀=131.2 g
• Agota el compustible en el instante, t_f=5.358 s
• Velocidad de salida de los gases, respecto del cohete, u=780.8 m/s
• Quema combustible a razón, D=8.343 g/s

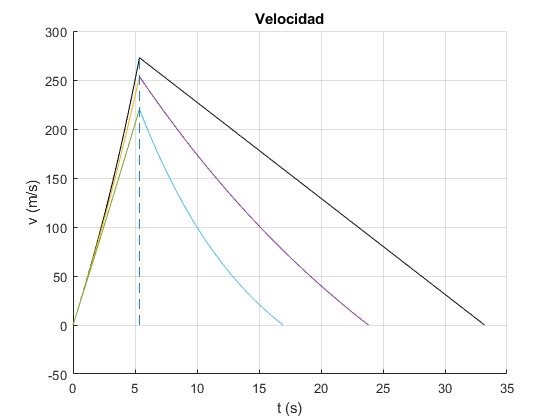
Representamos

• La velocidad del cohete v en función del tiempo, cuando no se tiene en cuenta el rozamiento, en color negro
• Cuando se tiene en cuenta el rozamiento, para dos valores del parametro b=0.003 y 0.009 kg/s

m0=131.2/1000; %masa inicial
tf=5.358; %agota combustible
D=8.343/1000; %kg/s
mf=m0-D*tf; %masa final
u=780.8; %m/s
hold on
%sin rozamiento
v=@(t) -9.8*t+u*log(m0./(m0-D*t));
fplot(v,[0,tf], 'color','k')
v1=v(tf);
fplot(@(t) v1-9.8*(t-tf), [tf,tf+v1/9.8], 'color','k')
%con rozamiento
for b=[3,9]/1000
    c=-(9.8*b*m0+u*D*(D-b))/(b*(D-b)*m0^(b/D));
    v=@(t) c*(m0-D*t).^(b/D)+9.8*(m0-D*t)/(D-b)+u*D/b;
    fplot(v,[0,tf])
    vf=v(tf);
    tt=tf+mf*log((mf*9.8+b*vf)/(mf*9.8))/b;
    v=@(t) (mf*9.8/b+vf)*exp(-b*(t-tf)/mf)-mf*9.8/b;
    fplot(v,[tf, tt])
end
line([tf,tf],[0,v1],'lineStyle','--') 
hold off
grid on
xlabel('t (s)')
ylabel('v (m/s)')
title('Velocidad')

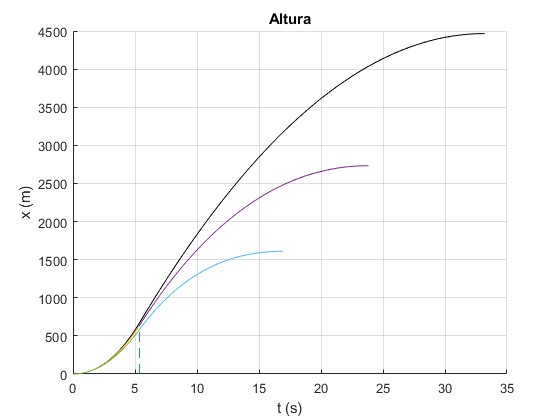
Representamos

• La altura del cohete x en función del tiempo, cuando no se tiene en cuenta el rozamiento, en color negro
• Cuando se tiene en cuenta el rozamiento, para dos valores del parametro b=0.003 y 0.009 kg/s

m0=131.2/1000; %masa inicial
tf=5.358; %se agota el combustible
D=8.343/1000; %kg/s
mf=m0-D*tf; %masa final
u=780.8; %m/s
hold on
%sin rozamiento
x=@(t) u*t-4.9*t.^2+u*(m0-D*t).*log(1-D*t/m0)/D;
v=@(t) -9.8*t+u*log(m0./(m0-D*t));
fplot(x,[0,tf], 'color','k')
x1=x(tf);
v1=v(tf);
fplot(@(t) x1+v1*(t-tf)-4.9*(t-tf).^2, [tf,tf+v1/9.8], 'color','k')
%con rozamiento
for b=[3,9]/1000
    c=-(9.8*b*m0+u*D*(D-b))/(b*(D-b)*m0^(b/D));
    v=@(t) c*(m0-D*t).^(b/D)+9.8*(m0-D*t)/(D-b)+u*D/b;
    x=@(t) u*D*t/b-4.9*(m0-D*t).^2/(D*(D-b))-c*(m0-D*t).^(b/D+1)/(D+b)
+4.9*m0^2/(D*(D-b))+c*m0^(b/D+1)/(D+b);
    fplot(x,[0,tf])
    vf=v(tf);
    xf=x(tf);
    tt=tf+mf*log((mf*9.8+b*vf)/(mf*9.8))/b;
    xx=@(t) xf+mf*(9.8*mf/b+vf)*(1-exp(-b*(t-tf)/mf))/b-9.8*mf*(t-tf)/b;
    fplot(xx,[tf, tt])
end
line([tf,tf],[0,x1],'lineStyle','--')
hold off
grid on
xlabel('t (s)')
ylabel('x (m)')
title('Altura')

Fuerza de rozamiento proporcional al cuadrado de la velocidad

En este caso F_r=bv². La ecuación del movimiemto de escribe

${\displaystyle \frac{dv}{dt}+\frac{b}{m}{v}^2+g-\frac{uD}{m}=\mathrm{0,}m=m_0-Dt}$

Es una ecuación del tipo

${\displaystyle \frac{dv}{dt}+a_2(t)v^2+a_0(t)=0}$

que es complicada de resolver

Definimos una nueva variable χ, tal que

${\displaystyle v=\frac{\frac{d\chi }{dt}}{a_2\chi }}$

Derivamos respecto del tiempo

${\displaystyle \frac{dv}{dt}=\frac{\frac{d^2\chi }{d{t}^2}{a}_2\chi -\left(\frac{d{a}_2}{dt}\chi +a_2\frac{d\chi }{dt}\right)\frac{d\chi }{dt}}{a_2^2{\chi }^2}=\frac{\frac{d^2\chi }{d{t}^2}}{a_2\chi }-\frac{\frac{d{a}_2}{dt}\frac{d\chi }{dt}}{a_2^2\chi }-\frac{{\left(\frac{d\chi }{dt}\right)}^2}{a_2{\chi }^2}}$

Introduciendo v y dv/dt en la ecuación diferencial, obtenemos

${\displaystyle a_2\frac{d^2\chi }{d{t}^2}-\frac{d{a}_2}{dt}\frac{d\chi }{dt}+a_0{a}_2^2\chi =0}$

Definimos una nueva variable ξ

${\displaystyle \xi =\frac{2}{D}\sqrt{bmg}}$

Cambiamos la variable t por ξ

${\displaystyle \begin{array}{l}\frac{d\chi }{dt}=\frac{d\chi }{d\xi }\frac{d\xi }{dt}=-\sqrt{\frac{bg}{m}}\frac{d\chi }{d\xi }=-\frac{2}{D}\frac{bg}{\xi }\frac{d\chi }{d\xi }\\ \frac{d^2\chi }{d{t}^2}=\frac{d}{dt}\left(\frac{d\chi }{dt}\right)=\frac{d}{d\xi }\left(\frac{d\chi }{dt}\right)\frac{d\xi }{dt}=\frac{d}{d\xi }\left(-\frac{2}{D}\frac{bg}{\xi }\frac{d\chi }{d\xi }\right)\frac{d\xi }{dt}=-\frac{2bg}{D}\frac{d}{d\xi }\left(\frac{1}{\xi }\frac{d\chi }{d\xi }\right)\left(-\frac{2}{D}\frac{bg}{\xi }\right)=\frac{4b^2{g}^2}{D^2}\frac{1}{{\xi }^3}\left(\frac{d^2\chi }{d{\xi }^2}\xi -\frac{d\chi }{d\xi }\right)\\ a_2=\frac{b}{m}=\frac{4b^{2}g}{D^2{\xi }^2}\\ \frac{d{a}_2}{dt}=\frac{d{a}_2}{d\xi }\frac{d\xi }{dt}=-\frac{8b^{2}g}{D^2{\xi }^3}\left(-\frac{2}{D}\frac{bg}{\xi }\right)=\frac{16b^3{g}^2}{D^3{\xi }^4}\\ a_0=g-\frac{uD}{m}=g-\frac{4bgu}{D{\xi }^2}\end{array}}$

Introducimos, a₀, a₂, da₂/dt, dχ/dt, d²χ/dt² en la ecuación diferencial, que se transforma en una ecuación de Bessel

${\displaystyle \begin{array}{l}\frac{d^2\chi }{d{\xi }^2}+\frac{1}{\xi }\frac{d\chi }{d\xi }+\left(1-\frac{4bu}{D{\xi }^2}\right)\chi =0\\ {\xi }^2\frac{d^2\chi }{d{\xi }^2}+\xi \frac{d\chi }{d\xi }+\left({\xi }^2-{\nu }^2\right)\chi =\mathrm{0,}{\nu }^2=\frac{4bu}{D}\end{array}}$

cuya solución es

${\displaystyle \chi (\xi )=c_1{J}_{\nu }(\xi )+c_2{Y}_{\nu }(\xi )}$

La expresión de la velocidad v(ξ) es

${\displaystyle \begin{array}{l}\frac{d\chi }{d\xi }=c_1\left(\frac{\nu J_{\nu }(\xi )}{\xi }-J_{\nu +1}(\xi )\right)+c_2\left(\frac{\nu Y_{\nu }(\xi )}{\xi }-Y_{\nu +1}(\xi )\right)\\ v=\frac{\frac{d\chi }{dt}}{a_2\chi }=\frac{-\frac{2}{D}\frac{bg}{\xi }\frac{d\chi }{d\xi }}{\frac{4b^{2}g}{D^2{\xi }^2}\chi (\xi )}=-\frac{D\xi \frac{d\chi }{d\xi }}{2b\chi (\xi )}=-\frac{D}{2b}\xi \frac{c_1\left(\frac{\nu J_{\nu }(\xi )}{\xi }-J_{\nu +1}(\xi )\right)+c_2\left(\frac{\nu Y_{\nu }(\xi )}{\xi }-Y_{\nu +1}(\xi )\right)}{c_1{J}_{\nu }(\xi )+c_2{Y}_{\nu }(\xi )}=\\ v(\xi )=\frac{D}{2b}\left(\xi \frac{J_{\nu +1}(\xi )+c{Y}_{\nu +1}(\xi )}{J_{\nu }(\xi )+c{Y}_{\nu }(\xi )}-\nu \right)\end{array}}$

La constante c se determina sabiendo que en el instante t=0, m=m₀, y v=v₀.

${\displaystyle \begin{array}{l}{v}_0=\frac{D}{2b}\left({\xi }_0\frac{J_{\nu +1}({\xi }_0)+c{Y}_{\nu +1}({\xi }_0)}{J_{\nu }({\xi }_0)+c{Y}_{\nu }({\xi }_0)}-\nu \right),{\xi }_0=\frac{2}{D}\sqrt{b{m}_{0}g}\\ c=\frac{\left(2b{v}_0+D\nu \right)J_{\nu }({\xi }_0)-D{\xi }_0{J}_{\nu +1}({\xi }_0)}{D{\xi }_0{Y}_{\nu +1}({\xi }_0)-\left(2b{v}_0+D\nu \right)Y_{\nu }({\xi }_0)}\end{array}}$

Si parte del reposo, v₀=0

${\displaystyle c=\frac{\nu J_{\nu }({\xi }_0)-{\xi }_0{J}_{\nu +1}({\xi }_0)}{{\xi }_0{Y}_{\nu +1}({\xi }_0)-\nu Y_{\nu }({\xi }_0)}}$

Altura

No hay solución analítica para determinar la altura x en función del tiempo t. Resolvemos la ecuación diferencial

${\displaystyle \frac{d^{2}x}{d{t}^2}+\frac{b}{m_0-Dt}{\left(\frac{dx}{dt}\right)}^2+g-\frac{uD}{m_0-Dt}=0}$

por el procedimiento numérico ode45 de MATLAB hasta el instante t_f, con las siguientes condiciones iniciales: en el instante t=0, x=0, dx/dt=0. Parte del origen en reposo

Se agota el combustible

En el instante t_f en el que se agota el combustible, la masa del cohete es m_f=m₀-D·t_f, su velocidad es v_f y su altura x_f. La ecuación del movimiento es

${\displaystyle \frac{dv}{dt}+\frac{b}{m_f}{v}^2+g=0}$

Integrando, obtenemos la velocidad v en función del tiempo t

${\displaystyle \begin{array}{l}-{\displaystyle \underset{v_f}{\overset{v}{\int }}\frac{dv}{g+\frac{b}{m_f}{v}^2}}={\displaystyle \underset{t_f}{\overset{t}{\int }}dt}\\ -\frac{m_f}{b}\frac{1}{\sqrt{\frac{m_{f}g}{b}}}\left\{\arctan \left(\sqrt{\frac{b}{m_{f}g}}v\right)-\arctan \left(\sqrt{\frac{b}{m_{f}g}}{v}_f\right)\right\}=t-t_f\\ v(t)=\sqrt{\frac{m_{f}g}{b}}\tan \left\{\arctan \left(\sqrt{\frac{b}{m_{f}g}}{v}_f\right)-\sqrt{\frac{bg}{m_f}}\left(t-t_f\right)\right\}\end{array}}$

Se alcanza la altura máxima en el instante t, cuando la velocidad es nula v=0

${\displaystyle t=t_f+\sqrt{\frac{m_f}{bg}}\arctan \left(\sqrt{\frac{b}{m_{f}g}}{v}_f\right)}$

Integramos de nuevo, para obtener la altura x en función del tiempo t

${\displaystyle \begin{array}{l}x(t)-x_f={\displaystyle \underset{t_f}{\overset{t}{\int }}v(t)·dt}\\ x(t)=x_f+\frac{m_f}{b}\ln \frac{\cos \left(\arctan \left(\sqrt{\frac{b}{m_{f}g}}{v}_f\right)-\sqrt{\frac{bg}{m_f}}\left(t-t_f\right)\right)}{\cos \left(\arctan \left(\sqrt{\frac{b}{m_{f}g}}{v}_f\right)\right)}=\\ x_f+\frac{m_f}{b}\ln \left\{\sqrt{1+\frac{b}{m_{f}g}{v}_f^2}\cos \left(\arctan \left(\sqrt{\frac{b}{m_{f}g}}{v}_f\right)-\sqrt{\frac{bg}{m_f}}\left(t-t_f\right)\right)\right\}\end{array}}$

Ejemplo

Sea un cohete

• Masa inicial, m₀=131.2 g
• Agota el compustible en el instante, t_f=5.358 s
• Velocidad de salida de los gases, respecto del cohete, u=780.8 m/s
• Quema combustible a razón, D=8.343 g/s

La masa final del cohete, cuando ha agotado el combustible es m_f=m₀-D·t_f

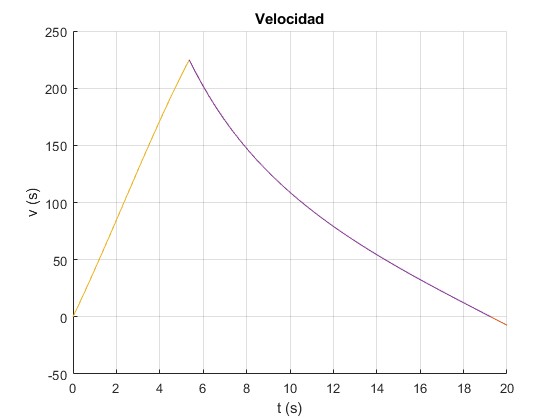
Representamos la velocidad v en función del tiempo t para b=5·10^-5 kg/m. Comprobamos que la solución numérica utilizando el procedimiento ode45 de MATLAB coincide, aproximadamente, con la solución analítica

m0=131.2/1000; %masa inicial
tf=5.358; %se agota el combustible
D=8.343/1000; %kg/s
mf=m0-D*tf; %masa final
u=780.8; %m/s
hold on
b=0.5/10000;
%solución numérica
f=@(t,x) [x(2);(u*D-b*x(2)^2)/(m0-D*t)-9.8];
[t,x]=ode45(f,[0,tf],[0,0]);
plot(t,x(:,2))
f=@(t,x) [x(2);(-b*x(2)^2)/mf-9.8];
[t,x]=ode45(f,[tf, 20],[x(end,1),x(end,2)]);
plot(t,x(:,2))
%solución analítica
nu=2*sqrt(b*u/D);
xi_0=2*sqrt(b*m0*9.8)/D;
c=(nu*besselj(nu,xi_0)-xi_0*besselj(nu+1,xi_0))/(xi_0*bessely(nu+1,xi_0)
-nu*bessely(nu,xi_0));
v=@(t) D*((2*sqrt(b*(m0-D*t)*9.8)/D).*(besselj(nu+1,2*sqrt(b*(m0-D*t)*9.8)/D)+
c*bessely(nu+1,2*sqrt(b*(m0-D*t)*9.8)/D))./(besselj(nu,2*sqrt(b*(m0-D*t)*9.8)/D)+
c*bessely(nu,2*sqrt(b*(m0-D*t)*9.8)/D))-nu)/(2*b);
fplot(v,[0,tf])
vf=v(tf);
tt=tf+sqrt(mf/(b*9.8))*atan(sqrt(b/(mf*9.8))*vf);
v=@(t) sqrt(mf*9.8/b)*tan(atan(sqrt(b/(mf*9.8))*vf)-sqrt(9.8*b/mf)*(t-tf));
fplot(v,[tf, tt])
hold off
grid on
xlabel('t (s)')
ylabel('v (s)')
title('Velocidad')

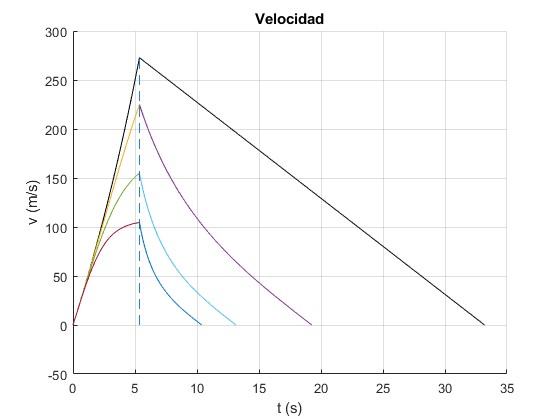
Representamos

• La velocidad del cohete v en función del tiempo, cuando no se tiene en cuenta el rozamiento, en color negro
• Cuando se tiene en cuenta el rozamiento, para los valores del parametro b=5·10^-5, 20·10^-5 y 50·10^-5 kg/m

m0=131.2/1000; %masa inicial
tf=5.358; %se agota el combustible
D=8.343/1000; %kg/s
mf=m0-D*tf; %masa final
u=780.8; %m/s
hold on
%sin rozamiento
v=@(t) -9.8*t+u*log(m0./(m0-D*t));
fplot(v,[0,tf], 'color','k')
v1=v(tf);
fplot(@(t) v1-9.8*(t-tf), [tf,tf+v1/9.8], 'color','k')
%con rozamiento
for b=[0.5,2,5]/10000
    nu=2*sqrt(b*u/D);
    xi_0=2*sqrt(b*m0*9.8)/D;
    c=(nu*besselj(nu,xi_0)-xi_0*besselj(nu+1,xi_0))/(xi_0*bessely(nu+1,xi_0)
-nu*bessely(nu,xi_0));
    v=@(t) D*((2*sqrt(b*(m0-D*t)*9.8)/D).*(besselj(nu+1,2*sqrt(b*(m0-D*t)*9.8)/D)+
c*bessely(nu+1,2*sqrt(b*(m0-D*t)*9.8)/D))./(besselj(nu,2*sqrt(b*(m0-D*t)*9.8)/D)+
c*bessely(nu,2*sqrt(b*(m0-D*t)*9.8)/D))-nu)/(2*b);
    fplot(v,[0,tf])
    vf=v(tf);
    tt=tf+sqrt(mf/(b*9.8))*atan(sqrt(b/(mf*9.8))*vf);
    v=@(t) sqrt(mf*9.8/b)*tan(atan(sqrt(b/(mf*9.8))*vf)-sqrt(9.8*b/mf)*(t-tf));
    fplot(v,[tf, tt])
end
line([tf,tf],[0,v1],'lineStyle','--')
hold off
grid on
xlabel('t (s)')
ylabel('v (m/s)')
title('Velocidad')

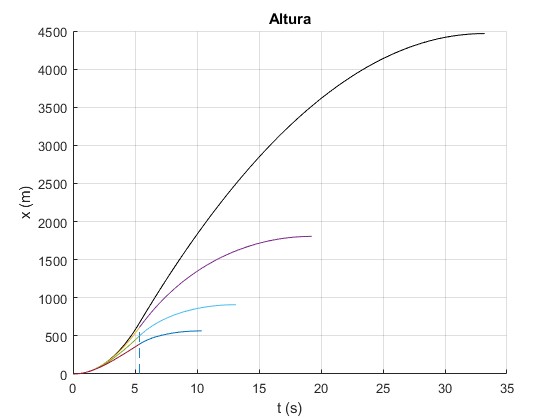
Representamos

• La altura del cohete x en función del tiempo, cuando no se tiene en cuenta el rozamiento, en color negro
• Cuando se tiene en cuenta el rozamiento, para los valores del parametro b=5·10^-5, 20·10^-5 y 50·10^-5 kg/m

m0=131.2/1000; %masa inicial
tf=5.358; %se agota el combustible
D=8.343/1000; %kg/s
mf=m0-D*tf; %masa final
u=780.8; %m/s
hold on
%sin rozamiento
x=@(t) u*t-4.9*t.^2+u*(m0-D*t).*log(1-D*t/m0)/D;
v=@(t) -9.8*t+u*log(m0./(m0-D*t));
fplot(x,[0,tf], 'color','k')
x1=x(tf);
v1=v(tf);
fplot(@(t) x1+v1*(t-tf)-4.9*(t-tf).^2, [tf,tf+v1/9.8], 'color','k')
%con rozamiento
for b=[0.5,2,5]/10000
    f=@(t,x) [x(2);(u*D-b*x(2)^2)/(m0-D*t)-9.8]; %solución numérica
    [t,x]=ode45(f,[0,tf],[0,0]);
    plot(t,x(:,1))
    vf=x(end,2);
    tt=tf+sqrt(mf/(b*9.8))*atan(sqrt(b/(mf*9.8))*vf);
    xf=x(end,1);
    xx=@(t) xf+mf*log(sqrt(1+b*vf^2/(9.8*mf))*cos(atan(sqrt(b/(mf*9.8))*vf)
-sqrt(9.8*b/mf)*(t-tf)))/b;
    fplot(xx,[tf, tt])
    line([tf,tf],[0,xf],'lineStyle','--')
end
hold off
grid on
xlabel('t (s)')
ylabel('x (m)')
title('Altura')

Referencias

André Luíz Alves, Sérgio Souza Bento, Carlos Henrique Marchi. Movimento Vertical de Minifoguetes: Equações de Trajetórias e Análises Gráficas. Vertical Model Rocket Movement: Trajectory Equations and Graphical Analysis. Revista Brasileira de Ensino de Física, vol. 43, e20200479 (2021)

H. Rodrigues, M.O. Pinho, D. Portes Jr., A. Santiago. Analytical description of ascending motion of rockets in the atmosphere. Eur. J. Phys. 30 (2009) pp. 185–190.