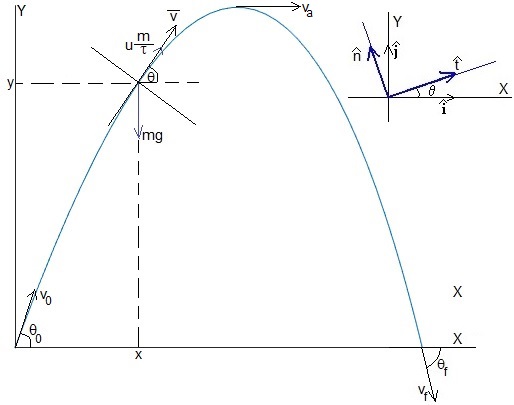
Cambiamos de sistema de referencia, escribiendo las ecuaciones del movimiento en la dirección tangencial y en la dirección normal

La relación entre los vectores unitarios (en la parte derecha de la figura) es

${\displaystyle \begin{array}{l}\{\begin{array}{l}\widehat{t}=\cos \theta \widehat{i}+\sin \theta \widehat{j}\\ \widehat{n}=-\sin \theta \widehat{i}+\cos \theta \widehat{j}\end{array}\\ \frac{d\widehat{t}}{dt}=\left(-\sin \theta \widehat{i}+\cos \theta \widehat{j}\right)\frac{d\theta }{dt}=\frac{d\theta }{dt}\widehat{n}\end{array}}$

La derivada del vector velocidad tiene dos componentes

${\displaystyle m\frac{d\overrightarrow{v}}{dt}=m\frac{d\left(v\widehat{t}\right)}{dt}=m\frac{dv}{dt}\widehat{t}+mv\frac{d\widehat{t}}{dt}=m\frac{dv}{dt}\widehat{t}+mv\frac{d\theta }{dt}\widehat{n}}$

Las fuerzas sobre el cohete de masa variable m son

• El peso, mg
• El empuje de los gases, um/τ, en el caso de que la masa del cohete disminuya exponencialmente con el tiempo

La segunda ley de Newton, en la dirección tangencial y en la dirección normal, es

${\displaystyle \{\begin{array}{l}m\frac{dv}{dt}=m\frac{u}{\tau }-mg\sin \theta \\ mv\frac{d\theta }{dt}=-mg\cos \theta \end{array}}$

Dividimos ambas ecuaciones

${\displaystyle \frac{dv}{v}=-\frac{\frac{u}{\tau }-g\sin \theta }{g\cos \theta }d\theta }$

Separamos las variables v y θ

${\displaystyle \frac{dv}{v}=-\frac{\frac{u}{\tau }-g\sin \theta }{g\cos \theta }d\theta }$

Integramos, sabiendo que en el punto de partida la velocidad inicial es v₀ haciendo un ángulo θ₀ con la horizontal

${\displaystyle \begin{array}{l}{\displaystyle \underset{v_0}{\overset{v}{\int }}\frac{dv}{v}}=-{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\frac{\frac{u}{\tau }-g\sin \theta }{g\cos \theta }d\theta }\\ \ln \left(\frac{v}{v_0}\right)=-\frac{u}{\tau g}{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\frac{d\theta }{\cos \theta }}+{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\tan \theta ·d\theta }\end{array}}$

La integral de la secante, 1/cosθ, se encuentra en la página titulada Integrales, las otras dos son inmediatas. El resultado es

${\displaystyle \begin{array}{l}\ln \left(\frac{v}{v_0}\right)={-\frac{u}{\tau g}\ln \left|\frac{1+\sin \theta }{\cos \theta }\right||}_{{\theta }_0}^{\theta }-{\ln \cos \theta |}_{{\theta }_0}^{\theta }=\ln {\left|\frac{\left(1+\sin {\theta }_0\right)\cos \theta }{\left(1+\sin \theta \right)\cos {\theta }_0}\right|}^{u/\left(\tau g\right)}+\ln \left|\frac{\cos {\theta }_0}{\cos \theta }\right|\\ v=v_0\left|\frac{\cos {\theta }_0}{\cos \theta }\right|{\left|\frac{\left(1+\sin {\theta }_0\right)\cos \theta }{\left(1+\sin \theta \right)\cos {\theta }_0}\right|}^{u/\left(\tau g\right)}\end{array}}$

La altura máxima (del vértice de la trayectoria) se obtiene para θ=0, la velocidad cuya dirección es horizontal vale, entonces

${\displaystyle v_a=v_0\cos {\theta }_0{\left(\frac{1+\sin {\theta }_0}{\cos {\theta }_0}\right)}^{u/\left(\tau g\right)}}$

Posición del cohete

Otra forma de escribir las ecuaciones del movimiento en la dirección tangencial y en la dirección normal

${\displaystyle \{\begin{array}{l}m\frac{dv}{dt}=m\frac{u}{\tau }-mg\sin \theta \\ m\frac{v^2}{\rho }=mg\cos \theta \end{array}}$

donde ρ es el radio de curvatura de la trayectoria.

En el intervalo de tiempo comprendido entre t y t+dt, la dirección del vector velocidad cambia un ángulo dθ, que es el ángulo entre las tangentes o entre las normales. El móvil se desplaza en este intervalo de tiempo un arco ds=ρ·dθ, tal como se aprecia en la figura.

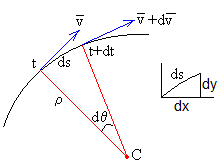
dx=ds·cosθ=ρdθ·cosθ

Utilizando la ecuación del movimiento en la dirección normal, y teniendo en cuenta que la trayectoria tiene curvatura negativa

${\displaystyle \begin{array}{l}dx=-\frac{v^2}{g\cos \theta }\cos \theta ·d\theta =-\frac{v^2}{g}d\theta \hfill \\ x=x_0-\frac{1}{g}{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}{v}^{2}d\theta }\hfill \end{array}}$

Del mismo modo

dy=ds·sinθ=ρdθ·sinθ

${\displaystyle \begin{array}{l}dy=-\frac{v^2}{g\cos \theta }\sin \theta ·d\theta =-\frac{v^2}{g}\tan \theta ·d\theta \hfill \\ y=y_0-\frac{1}{g}{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}{v}^2\tan \theta ·d\theta }\hfill \end{array}}$

Donde (x₀, y₀) es la posición inicial, normalmente el origen

La altura máxima se obtiene para θ=0

${\displaystyle H=-\frac{1}{g}{\displaystyle \underset{{\theta }_0}{\overset{0}{\int }}{v}^2\tan \theta ·d\theta }}$

Tiempo de vuelo

ds=v·dt
ρdθ= v·dt

${\displaystyle \begin{array}{l}dt=-\frac{v^2}{vg\cos \theta }d\theta =-\frac{v}{g\cos \theta }d\theta \\ t=-\frac{1}{g}{\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}\frac{v}{\cos \theta }d\theta }\end{array}}$

Alcance

Calculamos el ángulo θ_f final que forma la dirección de la velocidad cuando y=0, resolviendo la ecuación trascendente mediante fzero de MATLAB.

${\displaystyle {\displaystyle \underset{{\theta }_0}{\overset{\theta }{\int }}{v}^2\tan \theta ·d\theta }}$

Conocido el ángulo final θ_f se calcula el alcance R=x-x₀ y el tiempo de vuelo T, calculando las integrales por el procedimiento numérico integral de MATLAB

${\displaystyle R=-\frac{1}{g}{\displaystyle \underset{{\theta }_0}{\overset{{\theta }_f}{\int }}{v}^{2}d\theta },T=-\frac{1}{g}{\displaystyle \underset{{\theta }_0}{\overset{{\theta }_f}{\int }}\frac{v}{\cos \theta }d\theta }}$

Solucción numérica

Solamente hay solucción analítica para el módulo de la velocidad. Obtenemos la solucción numérica resolviendo el sistema de dos ecuaciones diferenciales con las condiciones iniciales siguientes: en el instante t=0, el cohete parte del origen (0,0) con velocidad inicial (dx/dt)₀=v₀cosθ₀ y (dy/dt)₀=v₀sinθ₀

${\displaystyle \begin{array}{l}\{\begin{array}{l}m\frac{d^{2}x}{d{t}^2}=m\frac{u}{\tau }\cos \theta \\ m\frac{d^{2}y}{d{t}^2}=m\frac{u}{\tau }\sin \theta -mg\end{array}\\ \{\begin{array}{l}\frac{d^{2}x}{d{t}^2}=\frac{u}{\tau }\frac{v_x}{v}\\ \frac{d^{2}y}{d{t}^2}=\frac{u}{\tau }\frac{v_y}{v}-g\end{array}\\ \{\begin{array}{l}\frac{d^{2}x}{d{t}^2}=\frac{u}{\tau }\frac{\frac{dx}{dt}}{\sqrt{{\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2}}\\ \frac{d^{2}y}{d{t}^2}=\frac{u}{\tau }\frac{\frac{dy}{dt}}{\sqrt{{\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2}}-g\end{array}\end{array}}$

Ejemplo

El cohete parte del origen con velocidad v₀=30 m/s, haciendo un ángulo θ₀=π/4 (45°). Calculamos

• el alcance, R
• el tiempo de vuelo, T
• la altura máxima, H
• el ángulo final, θ_f
• la velocidad final, v_f

Resolvemos numéricamente, mediante ode45 de MATLAB, el sistema de dos ecuaciones diferenciales, deteniendo la integración cuando y=0 (llega al suelo) y representamos la trayectoria

Comparamos los resultados

function cohete_2d
    u=400; %velocidad de salida de los gases
    v0=30; %velocidad inicial
    tau=35; %parámetro
    th_0=45*pi/180; %ángulo de tiro
    
    v=@(x) v0*abs(cos(th_0)./cos(x)).*abs((1+sin(th_0))*cos(x)./
((1+sin(x))*cos(th_0))).^(u/(tau*9.8));
    f=@(x) -tan(x).*(v(x).^2);
    g=@(y) integral(f,th_0,y);
    th_f=fzero(g,[-pi*80/180, th_0-eps]);
    hMax=integral(f,th_0,0)/9.8;
    f=@(x) -(v(x).^2)./9.8;
    xMax=integral(f,th_0,th_f);
    f=@(x) -v(x)./(9.8*cos(x));
    tVuelo=integral(f,th_0,th_f);
    fprintf('Exacta: altura máxima %2.1f, alcance %3.1f, tiempo de vuelo %1.2f, 
ángulo final %2.1f, velocidad final %2.2f\n', hMax, xMax, tVuelo, th_f*180/pi, 
v(th_f))

%sistema de dos ecuaciones diferenciales
    fg=@(t,x)[x(2);u*x(2)/sqrt(x(2)^2+x(4)^2)/tau; x(4);u*x(4)/
sqrt(x(2)^2+x(4)^2)/tau-9.8];
    opts=odeset('events',@stop_proyectil);
    [t,x]=ode45(fg,[0,10],[0,v0*cos(th_0),0,v0*sin(th_0)], opts);
    plot(x(:,1),x(:,3)) %trayectoria
    fprintf('Numérico: tiempo de vuelo %1.2f, alcance %3.1f, (vx=%2.2f, 
    vy=%2.2f) \n', t(end), x(end,1), x(end,2),x(end,4));    
    hold off
    grid on
    xlabel('x')
    ylabel('y')
    title('Movimiento de un cohete')

   function [detect,stopin,direction]=stop_proyectil(~,x)
        detect=x(3); 
        stopin=1; 
        direction=-1; 
   end
end

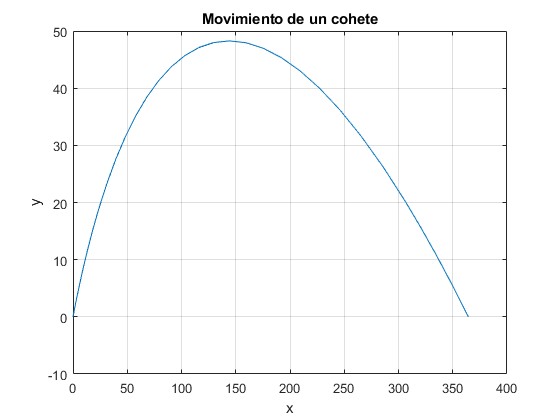
Exacta: altura máxima 48.3, alcance 364.4, tiempo de vuelo 6.58, 
ángulo final -21.0, velocidad final 98.22
Numérico: tiempo de vuelo 6.58, alcance 364.4, (vx=91.73, vy=-35.13) 

Los resultados coinciden por ambos procedimientos

Referencias

Yoonhwan Kang, Saebyok Bae. Two-dimensional motions of rockets. Eur. J. Phys. 28 (2007), pp. 135-144