Varilla que se mueve en un campo magnético que cambia con el tiempo.
Una varilla de longitud L y masa m se mueve sobre raíles paralelos separados una distancia a, tal como se muestra en la figura.
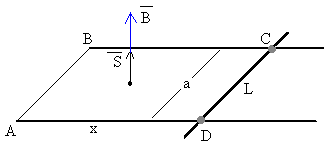
Cuando la varilla se encuentra en la posición x, el flujo del campo magnético a través de la espira ABCD es
La fem inducida es
Supongamos que la resistencia del lado CD del circuito es R y el resto es superconductor. La intensidad de la corriente inducida es
i=Vε/R
Si el campo B apunta hacia arriba y aumenta, el flujo Φ aumenta y la corriente inducida i, de acuerdo a la ley de Lenz tiene sentido de las agujas del reloj.
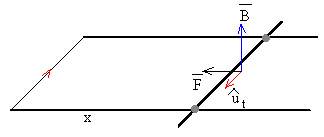
Una corriente i que circula por la porción de varilla de longitud a, experimenta una fuerza F en el seno de un campo magnético uniforme B.
donde es un vector unitario que señala la dirección y sentido del movimiento de los portadores de carga (positivos).
Como el campo magnético es perpendicular a la varilla. El módulo de la fuerza es
F=iBa
Es un vector paralelo a los raíles y cuyo sentido es hacia la izquierda, tal como se señala en la figura.
La ecuación del movimiento de la varilla es
Conocida la expresión del campo B en función del tiempo t, se resuelve esta ecuación diferencial por procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=0, la varilla se encuentra en la posición x0 en reposo dx/dt=0
Descripción cualitativa

Supondremos que el campo magnético crece rápidamente en un intervalo pequeño de tiempo y luego, se mantiene constante con valor B0. El movimiento de la varilla se divide en dos etapas:
-
En la primera etapa t<Δt, el primer término entre paréntesis predomina sobre el segundo, ya que dB/dt es grande al incrementarse B rápidamente. Supondremos que durante este breve tiempo la varilla no se habrá desplazado apreciablemente de su posición inicial x0.
-
En la segunda etapa t>Δt, el campo B se mantiene constante y dB/dt=0.
Integrando ambos miembros, con las condicione iniciales t=0, B=0, y dx/dt=0, y en el instante final B=B0, y dx/dt=vf.
Las condiciones iniciales son: en el instante t=0, x≈x0, B=B0 constante, y dx/dt=vf
La aceleración es de signo contrario a la velocidad, positiva, la varilla se frena. Integrando
Cuando la velocidad v se hace cero, la varilla se detiene en la posición
La posición final es la mitad de la posición inicial
Descripción cuantitativa.
Una función que describe bastante bien un campo magnético que crece rápidamente con el tiempo y luego, se mantiene constante B0 es
B=B0(1-exp(t/τ))
Donde τ se denomina constante de tiempo.
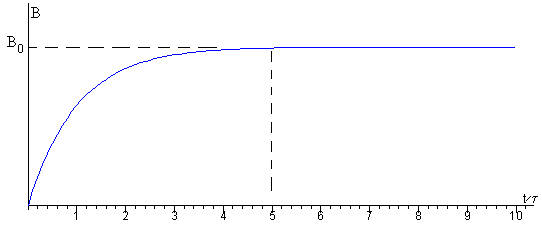
En el instante t=5τ, el valor del campo B=0.99B0 es prácticamente constante
Para describir el movimiento de la varilla tenemos que resolver la ecuación diferencial por procedimientos numéricos
con las condiciones iniciales siguientes: en el instante t=0, la varilla se encuentra en la posición x=x0, en reposo, dx/dt=0.
Los dos programas interactivos de esta página resuelven esta ecuación diferencial por el procedimiento de Runge-Kutta.
Actividades
Se introduce
-
El valor de la constante de tiempo τ, en el control titulado Constante de tiempo.
-
La posición inicial, de la varilla se ha fijado en x0=10
-
Se ha fijado el valor de la constante de proporcionalidad
-
El campo magnético es perpendicular al plano de los raíles y apunta hacia dentro.
Se pulsa el botón titulado Nuevo
Observamos las dos etapas del movimiento de la varilla:
-
Como el flujo aumenta y es hacia dentro, la corriente inducida tiene el sentido contrario a las agujas del reloj (positiva). La fuerza acelera la varilla hacia el origen (velocidad negativa), incrementando su velocidad.
-
La corriente inducida cambia de sentido, la fuerza frena la varilla hasta que se para, después de un tiempo teóricamente infinito.
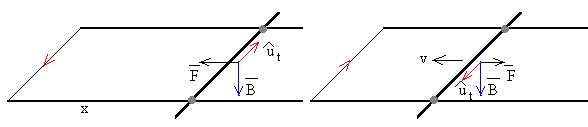
En la parte inferior, se representa
-
En color azul, el campo magnético B en función del tiempo t
-
En color rojo, la intensidad de la corriente inducida.
En la parte derecha, se proporcionan los datos de la velocidad v de la varilla y la intensidad i de la corriente inducida
Cuando la constante de tiempo es pequeña, por ejemplo, τ=0.1, el campo crece rápidamente en un tiempo muy corto y luego, se mantiene prácticamente constante. La varilla se detiene cerca de la posición calculada en el apartado descripción cualitativa: x=x0/2=10/2=5.
Ahora, examinamos el papel del campo magnético B0 y de la distancia a entre los raíles.
Se introduce
-
El campo magnético B0, en el control titulado Campo magnético
-
La distancia a entre los raíles, en el control titulado Distancia raíles
-
El valor de la constante de tiempo τ, en el control titulado Constante de tiempo.
Se pulsa el botón titulado Nuevo
Se representa mediante flechas
-
El vector campo magnético, hacia arriba o hacia abajo, según que B0 sea positivo o negativo, en color azul
-
El vector , que señala el sentido de la corriente inducida: i es la intensidad y es un vector unitario, en color rojo
-
El vector fuerza, en color negro.
Para un valor dado del la constante de tiempo τ
-
Cambiar el valor de B0, manteniendo la distancia a constante. Probar con B0 positivo y negativo.
-
Mantener B0 constante y cambiar el valor de a.
Mantener a y B0 constantes y cambiar el valor de la constante de tiempo τ
Referencias
Physics challenge for teachers and students, A faradayan slip April 2006, The Physics Teacher Vol 44, 2006

