El anillo de Thomson (II)

Demostración en el aula: el anillo de Thomson

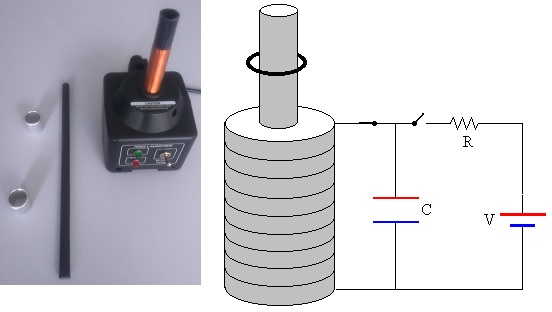
En el laboratorio de la Escuela de Ingeniería de Eibar disponemos de un equipo PASCO, denominado Ring launcher, que incluye un núcleo de hierro de 89 mm de altura y 11 mm de diámetro que se inserta en el solenoide, y dos anillos de aluminio de 12.81 g de masa, 25.5 mm de altura, 26.5 mm de diámetro exterior y 2.5 mm de espesor.

Los condensadores, la fuente y la resistencia forman un circuito RC, que se carga cuando se conecta a la fuente y se descarga cuando se conecta al solenoide.

El circuito RC de carga

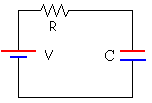
Estudiamos el proceso de carga y descarga de un condensador en serie con una resistencia.

Cuando se conecta el circuito RC a una fuente V, el condensador incrementa su carga con el tiempo hasta que adquiere una carga máxima Q, dada por

Q=V·C

El circuito RCL de descarga

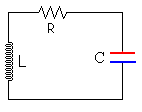
Una vez cargado el condensador, se desconecta de la batería y se conecta al solenoide.

La corriente en el solenoide se puede calcular suponiendo que forma parte de un circuito RCL.

Si el circuito tiene un comportamiento amortiguado γ<ω₀ la carga en el condensador disminuye con el tiempo de la forma

$q = A \exp (- γ t) \sin (ω t + ϕ) γ = \frac{R}{2 L} ω = \sqrt{\frac{1}{L C} - \frac{R^{2}}{4 L^{2}}}$

Las constantes A y φ se calculan a partir de las condiciones iniciales. En el instante t=0, el condensador se encuentra cargado con una carga Q o bien, la diferencia de potencia entre sus placas es V=Q/C, y la intensidad que circula por el circuito es cero I_s=dq/dt=0.

La expresiones de la carga del condensador y de la intensidad que circula por el solenoide son, respectivamente

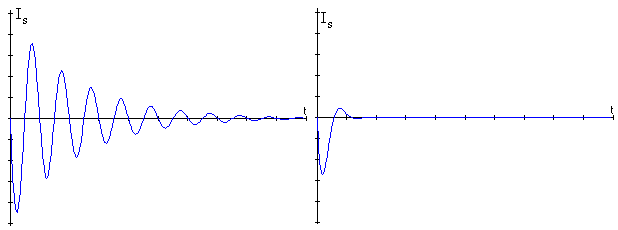
$\begin{array}{l} q = \frac{Q}{ω \sqrt{L C}} \exp (- γ t) \sin (ω t + ϕ) \sin ϕ = \frac{ω}{\sqrt{L C}} \\ I_{s} = \frac{d q}{d t} = - \frac{V}{L ω} \exp (- γ t) \sin (ω t) \end{array}$

En la figura, observamos la representación de la intensidad I_s en función del tiempo cuando la resistencia del circuito es pequeña (γ<<ω₀) y cuando es grande (γ<ω₀).

En la figura de la izquierda, apreciamos que la amplitud de la intensidad decrece exponencialmente con el tiempo, característica principal de las oscilaciones amortiguadas.

En la de la derecha, vemos que la intensidad crece (decrece) desde cero hasta un valor máximo (mínimo) en el instante t=π /(2ω ) y luego, decrece (crece) hasta hacerse próxima a cero.

Ley de Faraday

La corriente que circula por el solenoide produce un campo magnético que varía con el tiempo. El flujo Φ de dicho campo a través del anillo es

Φ =M·I_s

donde M es el coeficiente de inducción mutua del sistema formado por el solenoide y el anillo, I_s es de la intensidad de la corriente en el solenoide.

Aplicando la ley de Faraday, se obtiene la fem inducida V_a en el anillo como resultado del cambio del flujo que lo atraviesa con el tiempo. Aplicando la ley de Lenz, se determina el sentido de la corriente inducida.

$V_{ε} = - \frac{d Φ}{d t} = - M \cdot \frac{d I_{s}}{d t}$

La corriente inducida I_a en el anillo de resistencia R_a es

$I_{a} = \frac{V_{ε}}{R_{a}} = - \frac{M}{R_{a}} \frac{d I_{s}}{d t}$

Nos fijaremos principalmente en el comportamiento exponencial decreciente de la amplitud de la intensidad I_s. Expresamos la intensidad en el anillo como

I_a=-k·I_0s·exp(-γt)

Donde k es una constante de proporcionalidad que depende a su vez del tiempo.

Fuerza magnética sobre el anillo

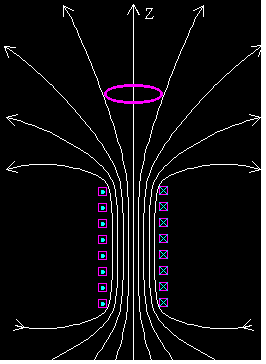
El campo magnético es paralelo al eje en el interior del solenoide, pero fuera del solenoide las líneas de campo divergen tal como se observa en la figura

El campo magnético del solenoide tiene simetría cilíndrica, y en la posición z que ocupa el anillo de radio a, el campo tiene dos componentes una a lo largo del eje Z, B_z y otra a lo largo de la dirección radial B_ρ.

La fuerza sobre el anillo es

$\vec{F} = I_{a} \oint^{} ({\hat{u}}_{t} \times \vec{B}) \cdot d l$

En la figura, vemos que la fuerza sobre un elemento de corriente dl tiene dos componentes

una a lo largo del eje Z, dF_z=-I_a·B_ρ·dl¸ (la corriente es positiva cuando circula en el sentido contrario a las agujas del reloj, el opuesto al que se muestra en la figura)
y otra, a lo largo de la dirección radial, dF_ρ=-I_a·B_z·dl.

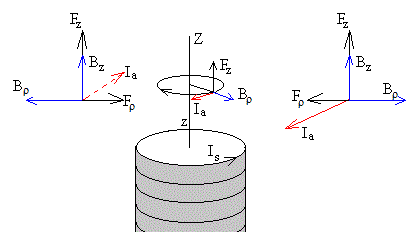
Las componentes radiales se anulan de dos en dos mientras que las componentes a lo largo del eje Z se suman. La fuerza resultante que ejerce el campo magnético $\vec{B}$ producido por el solenoide sobre la corriente inducida I_a en el anillo tiene la dirección del eje Z y su módulo vale

F_z=-2π a·I_a·B_ρ.

El campo B_ρ es proporcional a la corriente que circula por el solenoide (cuya amplitud decrece exponencialmente con el tiempo). Por otra parte, la amplitud de la corriente inducida I_a decrece exponencialmente con el tiempo. La amplitud de la fuerza sobre la espira también decrece exponencialmente con el tiempo.

Ecuación del movimiento del anillo

Mientras la intensidad en el solenoide crece de cero a su valor máximo en el instante t=π /(2ω), el anillo experimenta una intensa fuerza de repulsión durante un corto intervalo de tiempo.

Expresamos esta fuerza de la forma

$F = F_{0} \exp (- t / τ)$

La fuerza decrece exponencialmente con el tiempo con una constante tiempo τ que es mucho menor que el tiempo de vuelo del anillo.

Sobre el anillo actúan dos fuerzas, la fuerza magnética y el peso. Suponemos para no complicar excesivamente los cálculos que el rozamiento del aire es despreciable, lo que confirman los resultados experimentales.

$m \frac{d v}{d t} = F_{0} \exp (- t / τ) - m g$

Integrando respecto del tiempo, teniendo en cuanta que en el instante t=0, la velocidad inicial es cero v=0.

$v = \frac{F_{0}}{m} τ (1 - \exp (- t / τ)) - g t$

Integrando de nuevo respecto del tiempo, y teniendo en cuenta que para t=0, x=0.

$x = \frac{F_{0}}{m} τ [t - τ (1 - \exp (- t / τ))] - \frac{1}{2} g t^{2}$

La máxima altura se alcanza cuando v=0. Ahora bien, en el instante en el que se alcanza la máxima altura supondremos que ha transcurrido suficiente tiempo para la exponencial tenga un valor próximo a cero.

$t \approx \frac{F_{0} τ}{m g} x_{m á x} = \frac{1}{2} \frac{F_{0}^{2} τ^{2}}{m^{2} g} - \frac{F_{0} τ^{2}}{m g}$

Balance energético e impulso de la fuerza magnética

Si toda la energía almacenada en el condensador se convirtiese en energía potencial del anillo, se elevará a alturas muy grandes. Por ejemplo, para un condensador de 12.7 μ F cargado a una diferencia de potencial de 2000 V, la energía acumulada es CV²/2. La energía potencial de un anillo de cobre de 0.0389 kg que se ha elevado hasta una altura h es, mgh. Igualamos ambas energías y despejamos h=66.6 m. La elevación real de anillo es de unos cuantos centímetros como se podrá comprobar en la experiencia simulada.

Solamente una pequeña fracción f de la energía almacenada en el condensador se convierte en energía cinética inicial del anillo, el resto se pierde en las resistencias, radiación, etc.

$\frac{1}{2} m v_{0}^{2} = f \cdot \frac{1}{2} C V^{2}$

Por otra parte, la fuerza F de corta duración proporciona un impulso que hace que el anillo adquiera una velocidad inicial v₀.

$\int_{0}^{\infty} F_{0} \exp (- t / τ) d t = m v_{0} τ F_{0} = m v_{0}$

De ambas ecuaciones obtenemos el valor de F₀.

$F_{0} = \frac{m}{τ} \sqrt{\frac{f C}{m}} V$

Así pues, la dependencia de la altura máxima que alcanza el anillo con V ( diferencia de potencial entre las placas del condensador cargado) es de la siguiente forma

$x_{m á x} = \frac{f C}{2 m g} V^{2} - τ \sqrt{\frac{f C}{m}} V$

es decir

x_máx=AV²-BV

Donde A y B son parámetros a determinar en el ajuste de los datos experimentales a un polinomio de segundo grado, de los que se deducen f (fracción de energía del condensador que se convierte en energía mecánica) y τ (constante de tiempo de la fuerza magnética).

Ejemplo

Elegimos el anillo Cu (frío). Recogemos los siguientes datos

ddd (V)	600	800	1000	1200	1400	1600	1800	2000
h_máx	0.03	0.09	0.20	0.36	0.55	0.79	1.06	1.38

ddp=600:200:2000;
h=[0.03,0.09,0.20,0.36,0.55,0.79,1.06,1.38];
plot(ddp,h,'ro','linewidth',1,'markersize',4,'markeredgecolor',
'r','markerfacecolor','r')
title('Altura máxima')
xlabel('ddp (V)')
ylabel('h (m)')
grid on

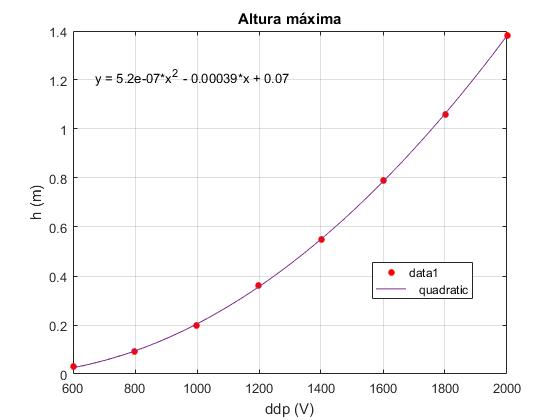
En el menú de la ventana gráfica, seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla quadratic en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p1 y p2 y p3 del polinomio y=p1*x^2 +p2*x+p3 de ajuste.

Actividades

En el programa interactivo se simula la experiencia descrita en el artículo mencionado en las referencias. Se elige un anillo entre cuatro posibilidades:

Anillo de cobre de 0.0389 kg de masa a temperatura normal o enfriado en nitrógeno líquido
Anillo de aluminio de 0.00752 kg de masa a temperatura normal o enfriado en nitrógeno líquido.

Se introduce

la diferencia de potencial V de la fuente de alta tensión entre 600 y 2000 V.

Se pulsa el botón titulado Nuevo.

Se observa como el anillo se eleva hasta una altura máxima, que puede medirse en una regla vertical dispuesta al efecto. Al lado del anillo, dos vectores representan las magnitudes relativas de la fuerza magnética (en rojo) y del peso (en azul).

En la parte derecha de la gráfica, se representa la velocidad del anillo en función del tiempo (en azul) y y la fuerza magnética sobre el anillo en función del tiempo. En la parte inferior se proporciona el dato de la altura máxima x_máx

ddp condensador
Anillos:

Referencias

Tanner P., Loebach J., Cook J., y Hallen H. D.. A pulsed jumping ring apparatus for demostration of Lenz’s law. Am. J. Phys. 69 (8) August 2001 pp. 911-916.