Campo magnético

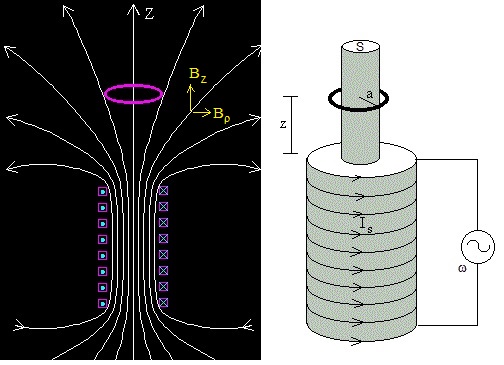
La corriente alterna I_s=I_0s·sin(ωt) que circula por el solenoide produce un campo magnético que varía con el tiempo.

El campo magnético es paralelo al eje en el interior del solenoide, pero fuera del solenoide las líneas de campo divergen tal como se observa en la figura. El campo magnético B tiene simetría cilíndrica, en la posición z del anillo tiene dos componentes:

• Componente a lo largo del eje vertical Z, B_z(t,z)=B_z(z)·sin(ωt)
• Componente a lo largo de la dirección radial, B_ρ(t,z)=B_ρ(z)·sin(ωt)

Fuerza sobre el anillo

La corriente variable I_s en el solenoide produce un campo magnético variable con el tiempo. La variación del flujo de dicho campo a través del anillo produce una fem. La corriente inducida en el anillo I_a se opone a las variaciones de dicho flujo de acuerdo a la ley de Lenz. En el aparato siguiente calcularemos la corriente inducida

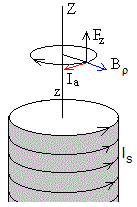
La fuerza magnética sobre la corriente inducida I_a que circula por el anillo es

${\displaystyle \overrightarrow{F}=I_a{{\displaystyle \oint }}^{\text{}}({\widehat{u}}_t\times \overrightarrow{B})·dl}$

La fuerza sobre un elemento de corriente dl tiene dos componentes:

1. Una a lo largo del eje Z, dF_z=I_a·B_ρ·dl¸, que se muestra en la figura
2. Otra a lo largo de la dirección radial, dF_ρ=I_a·B_z·dl.

Las componentes radiales de la fuerza se anulan de dos en dos mientras que las componentes a lo largo del eje Z se suman. La fuerza resultante que ejerce el campo magnético $\overrightarrow{B}$ producido por el solenoide sobre la corriente inducida I_a en el anillo tiene la dirección del eje Z y su módulo vale

F_z(t,z)=-2πa·I_a·B_ρ(t,z)=-2πa·I_a·B_ρ(z)·sin(ωt)

El signo negativo, indica que el sentido de la corriente inducida I_a es el de las agujas del reloj

El anillo como circuito R-L conectado a una fem alterna

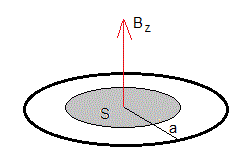
Si el campo magnético está confinado en el núcleo de hierro de sección S, el flujo del campo magnético a través del anillo es Φ=B_z(t,z)·S y la fem es

${\displaystyle V_a=-\frac{d\Phi }{dt}=-\omega S{B}_z(z)\cos (\omega t)}$

El anillo es un circuito R-L en serie conectado a una fem alterna de la forma V_a=-V_0acos(ωt).

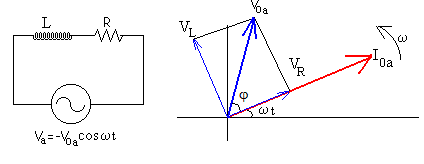
• La diferencia de potencial en los extremos de la autoinducción L está adelantada 90º respecto de la intensidad que circula por ella. La relación de amplitudes es V_L=I₀·ω L.
• La diferencia de potencial entre los extremos de la resistencia R está en fase con la intensidad. La relación de amplitudes es V_R=I₀·R.

Como vemos en la figura la fem V_a, está adelantada un ángulo φ respecto de la intensidad I_a.

${\displaystyle \tan \phi =\frac{V_L}{V_R}=\frac{\omega L}{R}}$

La intensidad de la corriente inducida en el anillo en función del tiempo es

${\displaystyle \begin{array}{l}Z=\sqrt{R^2+{\omega }^2{L}^2}\\ I_a=-\frac{\omega S{B}_z(z)}{\sqrt{R^2+{\omega }^2{L}^2}}\cos \left(\omega t-\phi \right)=-\frac{S{B}_z(z)}{L}\sin \phi \cos \left(\omega t-\phi \right)\end{array}}$

La fuerza sobre el anillo es

${\displaystyle F(t,z)=2\pi a{B}_{\rho }(z)\sin (\omega t)\frac{S{B}_z(z)}{L}\sin \phi \cos \left(\omega t-\phi \right)}$

El valor medio de la función f(t)=sin(ωt)·cos(ωt-φ) es

${\displaystyle <f(t)>=\frac{1}{P}{\displaystyle {\int }_0^{P}f(t)dt}=\frac{1}{\pi /\omega }\left(\frac{1}{2}\cos \phi {\displaystyle \underset{0}{\overset{\pi /\omega }{\int }}\sin (2\omega t)dt}+\sin \phi {\displaystyle \underset{0}{\overset{\pi /\omega }{\int }}{\sin }^2(\omega t)dt}\right)=\frac{1}{2}\sin \phi }$

>> syms w phi t;
>> y=sin(w*t)*cos(w*t-phi);
>> int(y,t,0,pi/w)*w/pi
ans = sin(phi)/2

• El primer término, sin(ωt)·cos(ωt), viene de la parte de la corriente en el anillo que está en fase con la fem y por tanto, desfasada 90º con la corriente en el solenoide. Produce una fuerza que oscila con una frecuencia 2ω y por tanto, su promedio en el tiempo es cero.

• El segundo término, sin(ωt)·sin(ωt), proviene de la parte inductiva de la corriente que tiene un desfase de 90º respecto de la fem y en fase con la corriente en el solenoide y es la que produce la fuerza de elevación sobre el anillo.

El valor medio de la fuerza es

${\displaystyle F(z)=B_{\rho }(z)B_z(z)\frac{\pi aS}{L}{\sin }^2\phi }$

Así pues, para que la fuerza sobre el anillo tenga un valor medio no nulo, tiene que existir un desfase φ entre la fem en el anillo y la corriente inducida en el mismo y este desfase se produce si consideramos que el anillo tiene una autoinducción L no nula.

Ejemplo:

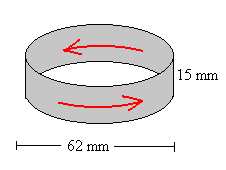
En el laboratorio disponemos de un anillo de aluminio de 62 mm de diámetro, 15 mm de longitud y 1 mm de espesor. La resistencia del anillo se calcula mediante la fórmula

${\displaystyle R=\rho \frac{l}{S}}$

Para el anillo de aluminio de las dimensiones señaladas ρ =2.8·10^-8 Ω·m, S=(1 mm·15 mm)=15·10^-6 m² y l=π·62 mm=π ·62·10^-3 m.

R=3.63·10^-4 Ω .

Existe una fórmula que nos permite calcular la autoinducción L de un anillo de forma toroidal de diámetro medio D y cuya sección es un círculo de diámetro d

${\displaystyle L={\mu }_0\frac{D}{2}\left(\ln \frac{8D}{d}-\frac{7}{4}\right)}$

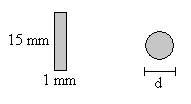
El área de la sección rectangular del anillo, es equivalente al área de la sección circular de una anillo toroidal de diámetro d tal que

15·1=πd²/4    d=4.37 mm

${\displaystyle L=4\pi ·{10}^{-7}\frac{0.062}{2}\left(\ln \frac{8·0.062}{0.00437}-\frac{7}{4}\right)=1.16·{10}^{-7}\text{H}}$

Para una fem de frecuencia f=50 Hz, ω=2πf=100π rad/s el desfase es

${\displaystyle \text{tan}\phi \text{=}\frac{\text{100}\pi 1.16·{10}^{-7}}{3.63·{10}^{-4}}=0.1\phi =5.7º}$

El valor medio de la fuerza <F_z> sobre el anillo es proporcional a sin²φ=0.01

Representamos el campo magnético B, la fem inducida V_ε, la intensidad i de la corriente en el anillo y la fuerza F que el campo magnético ejerce sobre la corriente inducida en el anillo. En esta última gráfica, señalamos mediante una línea horizontal de color azul, la fuerza media sobre el anillo

desfase=pi/6;
t=(1:360)*pi/180;
subplot(3,1,1)
x=sin(t);
plot(t,x,'k')
set(gca,'XTick',0:pi/2:2*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
xlim([0,2*pi])
grid on
xlabel('t')
ylabel('B')
subplot(3,1,2)
x=-cos(t);
hold on
plot(t,x, 'b')
x=-cos(t-desfase);
plot(t,x, 'r')
hold off
set(gca,'XTick',0:pi/2:2*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
xlim([0,2*pi])
grid on
xlabel('t')
ylabel('V_e,i')
subplot(3,1,3)
x=cos(t-desfase).*sin(t);
fMedia=sin(desfase)^2;
hold on
plot(t,x,'m')
line([0,2*pi],[fMedia,fMedia]);
set(gca,'XTick',0:pi/2:2*pi)
set(gca,'XTickLabel',{'0','\pi/2','\pi','3\pi/2','2\pi'})
xlim([0,2*pi])
grid on
xlabel('t')
ylabel('fuerza')

Actividades

En el programa interactivo de esta página, se ha sustituido el solenoide por una bobina, ya que es más sencillo de calcular el campo magnético creado por una bobina, que por un solenoide. El resultado final del "experimento" no cambia desde el punto de vista cualitativo.

Se calcula la fuerza que ejerce una bobina de 100 vueltas sobre un anillo situado a una altura z.

Se introduce

• La amplitud de la intensidad I_s0 que circula por la bobina, en el control titulado Intensidad
• La resistencia R del anillo (en unidades 10^-4 Ω), en el control titulado Resistencia
• La autoinducción L del anillo (en unidades 10^-7 H), en el control titulado Autoinducción
• La posición z del anillo en el control titulado Posición

Se ha fijado la frecuencia f=50 Hz

Se pulsa el botón titulado Nuevo

A partir de las dimensiones del anillo y del material del que está hecho, podríamos calcular su resistencia y autoinducción. Sin embargo, en el programa interactivo introducimos directamente estas dos magnitudes, para poder ensayar todas las posibilidades, un anillo con o sin resistencia, con o sin autoinducción.

El programa representa la fuerza sobre el anillo en color rojo y la fuerza media (una línea horizontal de color azul). Permite por tanto, examinar la fuerza magnética sobre el anillo cambiando los distintos parámetros.

El programa visualiza el movimiento de las cargas (en color rojo) en el solenoide y en el anillo, dándonos una idea del sentido de la corriente inducida.

Referencias

Celso L Ladera, Guillermo Donoso. Unveiling the physics of the Thomson jumping ring. Am. J. Phys. 83(4) April 2015, pp. 341-348

Hall J. Forces on the jumping ring. The Physcis Teacher, Vol. 35 February 1997 pp, 80-83.

Tjossem P., Cornejo V. Measurements and mechanisms of Thomson’s jumping ring. Am. J. Phys. 68 (3) March 2000, pp 238-244