Autoinducción nula (R≠ 0, L=0)

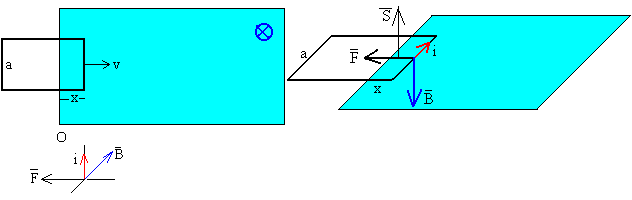
Si la espira de anchura a, se ha introducido x en la región en la que existe campo magnético que apunta perpendicularmente al plano del dibujo y hacia dentro, el flujo a través de la espira será

${\displaystyle \Phi =\overrightarrow{B}·\overrightarrow{S}=-B(ax)}$

Aplicando la ley de Faraday se obtiene la fem

${\displaystyle V_{\epsilon }=\frac{d\Phi }{dt}=Bav}$

De acuerdo a la ley de Lenz el sentido de la corriente inducida i es antihorario, ya que el flujo aumenta.

Para una espira de resistencia R, la ecuación del circuito es Vε =iR

${\displaystyle i=\frac{Bav}{R}}$

La fuerza sobre el lado derecho de la espira es

${\displaystyle \overrightarrow{F}=i·{\widehat{u}}_t\times \overrightarrow{B}·lF=-iBa=-\frac{B^2{a}^2}{R}v}$

de sentido contrario a la velocidad v de la espira.

La ecuación del movimiento de la espira será

${\displaystyle m\frac{dv}{dt}=-\frac{B^2{a}^2}{R}v}$

y la solución de la ecuación diferencial, con las condiciones iniciales t=0, v=v₀, es

${\displaystyle \begin{array}{l}{\displaystyle \underset{v_0}{\overset{v}{\int }}\frac{dv}{v}}=-\frac{B^2{a}^2}{Rm}{\displaystyle \underset{0}{\overset{t}{\int }}dt}\\ v=v_0\exp \left(-\frac{t}{\tau }\right),\tau =\frac{Rm}{B^2{a}^2}\end{array}}$

La velocidad v de la espira disminuye exponencialmente con el tiempo.

A partir de la expresión de la velocidad en función del tiempo obtenemos la posición x del móvil que parte del origen en el instante inicial t=0, x=0

${\displaystyle x=\underset{0}{\overset{t}{{\displaystyle \int }}}vdt=v_0\tau \left(1-\exp \left(-\frac{t}{\tau }\right)\right)}$

La intensidad en función del tiempo es

${\displaystyle i=\frac{Ba}{R}{v}_0\exp \left(-\frac{t}{\tau }\right)}$

La intensidad i que circula por la espira disminuye exponencialmente con el tiempo.

Alternativamente, expresamos la velocidad v en función de la posición x

${\displaystyle \begin{array}{l}\frac{dv}{dx}\frac{dx}{dt}=-\frac{B^2{a}^2}{mR}v\\ \frac{dv}{dx}=-\frac{B^2{a}^2}{mR}\\ {\displaystyle \underset{v_0}{\overset{v}{\int }}dv}=-\frac{1}{\tau }{\displaystyle \underset{0}{\overset{x}{\int }}dx}\\ v=v_0-\frac{x}{\tau }\end{array}}$

La velocidad disminuye linealmente con x

Estas ecuaciones se aplican mientras que el lado derecho de la espira esté en el seno del campo magnético. Cuando ambos lados estén dentro de la región x≥ 0, la intensidad de la corriente inducida será cero y la fuerza que ejerce el campo magnético sobre la espira será nula y por tanto, la velocidad de la espira será constante.

Estudio energético

Comprobamos que la energía cinética inicial de la espira E_k, se disipa en la resistencia de la espira. La ley de Joule afirma que la energía por unidad de tiempo (potencia) disipada en la resistencia es i²R.

En cualquier instante, la suma de la energía cinética E_k de la espira y de la energía disipada en la resistencia E_R es igual a la energía cinética inicial de la espira.

${\displaystyle \begin{array}{l}{E}_k=\frac{1}{2}m{v}^2=\frac{1}{2}m{v}_0^2\exp (-2t/\tau )\\ E_R={\displaystyle \underset{0}{\overset{t}{\int }}{i}^{2}R·dt=}\frac{1}{2}m{v}_0^2\left(1-\exp (-2t/\tau )\right)\\ E_k+E_R=\frac{1}{2}m{v}_0^2\end{array}}$

Ejemplo

Una espira cuadrada de lado a entra en una región de anchura b>a donde hay un campo magnético constante B uniforme apuntando hacia dentro de la pantalla. La velocidad inicial de la espira es v₀.

Vamos a calcular la velocidad final v₂ de la espira cuando sale de dicha región y el tiempo T empleado en atravesarla.

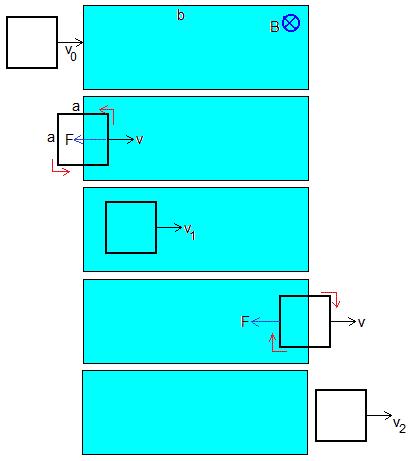
Se trata de una variante de la situación estudiada en la página titulada Una espira que se mueve a través de un campo magnético uniforme

• Cuando la espira entra en la región donde hay campo magnético

Cuando ya ha entrado, el lado derecho se ha desplazado a y la velocidad de la espira es

${\displaystyle v_1=v_0-\frac{a}{\tau }}$

y ha empleado un tiempo t₁

${\displaystyle v_1=v_0\exp \left(-\frac{t_1}{\tau }\right),t_1=\tau \ln \left(\frac{v_0}{v_1}\right)=\tau \ln \left(\frac{v_0\tau }{v_0\tau -a}\right)}$

• Se mueve en el interior de dicha región

Se mueve con velocidad constante, v₁. El lado derecho se desplazado b-a, empleando un tiempo t₂

${\displaystyle t_2=\frac{b-a}{v_1}=\frac{b-a}{v_0\tau -a}\tau }$

• La espira sale de la región

Su velocidad disminuye. Cuando ha salido completamente, la velocidad de la espira es v₂

${\displaystyle v_2=v_1-\frac{a}{\tau }=v_0-2\frac{a}{\tau }}$

Empleando un tiempo t₃

${\displaystyle v_2=v_1\exp \left(-\frac{t_3}{\tau }\right),t_3=\tau \ln \left(\frac{v_1}{v_2}\right)=\tau \ln \left(\frac{v_0\tau -a}{v_0\tau -2a}\right)}$

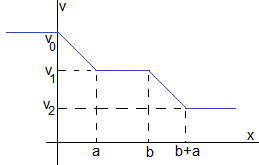
Representamos la velocidad v de la espira en función de la posición x del lado derecho de la espira

El tiempo total T=t₁+t₂+t₃ es

${\displaystyle \begin{array}{l}T=\tau \ln \left(\frac{v_0\tau }{v_0\tau -a}\right)+\frac{b-a}{v_0\tau -a}\tau +\tau \ln \left(\frac{v_0\tau -a}{v_0\tau -2a}\right)=\\ \tau \left\{\frac{b-a}{v_0\tau -a}+\ln \left(\frac{v_0\tau }{v_0\tau -2a}\right)\right\}\end{array}}$

Resistencia nula (L≠ 0, R=0)

Consideremos que la espira está hecha de un material superconductor de modo que R≈0. En este caso, no podemos ignorar la autoinducción L, que produce una fem

${\displaystyle V_L=-L\frac{di}{dt}}$

La ecuación del circuito (suma de fems igual a intensidad por resistencia) se escribe ahora V_L+V_ε =0.

${\displaystyle -L\frac{di}{dt}+Ba\frac{dx}{dt}=0i=\frac{Ba}{L}x}$

que satisface la condición inicial x=0, i=0.

La fuerza que ejerce el campo magnético sobre el lado derecho de la espira será de nuevo F=-iaB, por lo que la ecuación del movimiento se escribirá

${\displaystyle m\frac{d^{2}x}{d{t}^2}+\frac{B^2{a}^2}{L}x=0}$

Esta es la ecuación diferencial de un Movimiento Armónico Simple, x=A·sin(ω₀ t+φ ).

A partir de las condiciones iniciales para t=0, x=0, dx/dt=v₀ calculamos la amplitud A y la fase inicial φ .

${\displaystyle \begin{array}{l}x=\frac{v_0}{{\omega }_0}\sin {\omega }_{0}t{\omega }_0=\frac{Ba}{\sqrt{mL}}\\ v=v_0\cos {\omega }_{0}t\end{array}}$

Siempre que la amplitud de la oscilación v₀/ω₀ no sea mayor que la longitud de la espira, de modo que la espira no esté completamente introducida en la región x≥ 0, la espira describirá un MAS con frecuencia angular ω₀ y periodo P=2π/ω₀.

La intensidad de la corriente vale

${\displaystyle i=\frac{Ba}{L}x=v_0\sqrt{\frac{m}{L}}\sin ({\omega }_{0}t)}$

La máxima intensidad no depende de la anchura a de la espira, ni del campo magnético B.

Estudio energético

La energía cinética de la espira más la energía acumulada en la autoinducción en forma de campo magnético debe de ser constante e igual a la energía cinética inicial.

${\displaystyle \begin{array}{l}{E}_k=\frac{1}{2}m{v}^2=\frac{1}{2}m{v}_0^2{\cos }^2({\omega }_{0}t)\\ E_L=\frac{1}{2}L{i}^2=\frac{1}{2}\frac{B^2{a}^2}{L^2}{x}^2=\frac{1}{2}m{v}_0^2{\sin }^2({\omega }_{0}t)\\ E_k+E_L=\frac{1}{2}m{v}_0^2\end{array}}$

Actividades

En el programa interactivo que viene a continuación, se estudia el comportamiento de una espira que viaja hacia una región (x≥ 0) en la que existe un campo magnético uniforme perpendicular al plano de la espira: hacia adentro, negativo, en color azul claro o hacia fuera, positivo, en color rosa.

Se introduce

• la intensidad B del campo magnético (T) un número positivo o negativo
• la velocidad inicial v₀ (m/s)
• La masa de la espira se ha fijado en m=0.1 kg
• La anchura de la espira se ha fijado en a=0.25 m

Tenemos dos opciones

• Resistencia R (en unidades 10^-3 Ω) no nula, autoinducción nula
• Autoinducción L (en unidades 10^-5 H) no nula, resistencia nula.

Se pulsa el botón titulado Nuevo para situar la espira en la posición de partida, y el botón   ►   para poner en movimiento la espira.

• En la parte superior, observamos el movimiento de la espira, su posición y velocidad en función del tiempo.

• El sentido de la corriente inducida en la espira representada por el movimiento de puntos de color rojo.

• La representación gráfica de la intensidad de la corriente inducida en función del tiempo, en la parte inferior derecha. Se puede modificar la escala vertical de dicha representación en el control titulado Escala.

• En un gráfico en forma de tarta, en la parte inferior izquierda se efectúa el balance energético de este dispositivo electromecánico. Se representa la energía cinética de la espira (en color azul), la energía almacenada en forma de campo magnético en la autoinducción (en color rojo) y la energía disipada en la resistencia por efecto Joule (en color negro).

En el caso de que la espira tenga autoinducción no nula, el lado izquierdo de la espira estará siempre en la región x<0, en la que no hay campo magnético. Si se introduce una velocidad v₀ excesiva de la espira el programa no prosigue y nos invita a modificar el valor de la velocidad inicial de la espira. Para ello, la longitud de la espira ha de ser mayor que la amplitud v₀/ω₀ de las oscilaciones de la espira.

Ejemplo 1.

• m=0.1 kg
• a=0.25 m
• B=0.1 T (hacia dentro)
• v₀=2.0 m/s
• R=0.5·10^-3 Ω
• L=0

La constante de tiempo τ vale

${\displaystyle \tau =\frac{Rm}{B^2{a}^2}=\frac{0.5·{10}^{-3}·0.1}{{0.1}^2·{0.25}^2}=0.08}$

La espira se introduce en la región en la que existe campo magnético.

En el instante t=0.2 s la velocidad de la espira es

${\displaystyle v=2.0·\exp (-0.2/0.08)=0.16\text{m/s}}$

La posición del lado de la espira es

${\displaystyle x=2·0.08\left(1-\exp (-0.2/0.08)\right)=0.15\text{m}}$

La intensidad de la corriente en este instante vale

${\displaystyle i=\frac{Bav}{R}=\frac{0.1·0.25·0.16}{0.5·{10}^{-3}}=8.21\text{A}}$

Como el flujo aumenta, la intensidad (en sentido antihorario) se opone al aumento de flujo

Ejemplo 2.

• m=0.1 kg
• a=0.25 m
• B=0.1 T (hacia dentro)
• v₀=2.0 m/s
• R=0
• L=8·10^-5 H

La frecuencia angular ω₀ del MAS vale

${\displaystyle {\omega }_0=\frac{Ba}{\sqrt{mL}}=\frac{0.1·0.25}{\sqrt{0.1·8·{10}^{-5}}}=8.84\text{rad/s}}$

El semiperiodo, tiempo que tarda en entrar y salir la espira es P/2=π/ ω₀=0.36 s

La espira penetra hasta una distancia

${\displaystyle x_m=\frac{v_0}{{\omega }_0}=\frac{2.0}{8.84}=0.23\text{m}}$

La intensidad máxima en este instante es

${\displaystyle i_m=\frac{Ba}{L}{x}_m=\frac{0.1·0.25}{8·{10}^{-5}}0.23=70.7\text{A}}$

Resistencia y autoinducción no nulas (L≠ 0, R≠ 0)

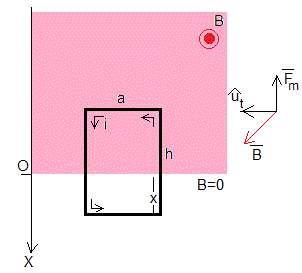
En este apartado se estudian las oscilaciones amortiguadas, críticas y sobreamortiguadas de la espira, siempre que que cumpla la condición de que solamente su lado superior esté en el interior del campo magnético x≥0.

Consideremos una región en la que existe un campo magnético uniforme B perpendicular al plano de la espira, en todos los puntos x≤0, y está libre de campo para x>0. Una espira de dimensiones a y h, se mueve hacia la región donde el campo es nulo x>0. El flujo del campo magnético a través de la espira disminuye y se generará una corriente inducido en el sentido contrario a las agujas del reloj tal como se incia en la figura.

El flujo total a través de la espira es la suma del flujo producido por el campo magnético externo, Ba(h-x) y el flujo propio, Li. Donde L es la autoinducción d ela espira

${\displaystyle \Phi =Ba(h-x)+Li}$

La fem inducida es

${\displaystyle V_{\epsilon }=-\frac{d\Phi }{dt}=Ba\frac{dx}{dt}-L\frac{di}{dt}}$

• La ecuación del circuito es (suma de fems igual a intensidad por resistencia)

${\displaystyle iR=Ba\frac{dx}{dt}-L\frac{di}{dt}}$

El campo magnético ejerce una fuerza magnética $\overrightarrow{F_m}=i{\widehat{u}}_t\times \overrightarrow{B}a$ sobre el lado superior de la espira, cuyo módulo es F_m=iBa. La fuerza que ejerce el campo magnético sobre los lados verticales de la espira son perpendiculares a dichos lados y no influyen en el movimiento vertical de la espira.

• La ecuación del movimiento es

${\displaystyle m\frac{dv}{dt}=mg-iBa}$

Despejando la intensidad i en la ecuación del movimiento e introduciéndola en la ecuación del circuito, llegamos a la siguiente ecuación diferencial de segundo orden

${\displaystyle \frac{d^{2}v}{d{t}^2}+\frac{R}{L}\frac{dv}{dt}+\frac{B^2{a}^2}{mL}v=g\frac{R}{L}}$

Que describe las oscilaciones amortiguadas

${\displaystyle \frac{d^{2}v}{d{t}^2}+2\gamma \frac{dv}{dt}+{\omega }_0^{2}v=2\gamma g{\omega }_0^2=\frac{B^2{a}^2}{mL}\gamma =\frac{R}{2L}}$

La solución particular de la ecuación diferencial es una constante C, cuyo valor es

${\displaystyle C=\frac{2\gamma g}{{\omega }_0^2}=\frac{mgR}{B^2{a}^2}}$

La ecuación diferencial homogénea con las condiciones iniciales:

${\displaystyle t=\mathrm{0,}v=\mathrm{0,}\frac{dv}{dt}=0}$

tiene tres posibles soluciones:

Oscilaciones amortiguadas

Si la resistencia R no es muy grande de modo que γ<ω₀

${\displaystyle \begin{array}{l}v=\exp (-\gamma t)\left(A\cos (\omega t)+B\sin (\omega t)\right)+\frac{2\gamma g}{{\omega }_0^2},{\omega }^2={\omega }_0^2-{\gamma }^2\\ \frac{dv}{dt}=-\gamma \exp (-\gamma t)\left(A\cos (\omega t)+B\sin (\omega t)\right)+\omega \exp (-\gamma t)\left(-A\sin (\omega t)+B\cos (\omega t)\right)\end{array}}$

donde ω es la frecuencia de las oscilaciones amortiguadas. Las constantes A y B se determinan a partir de las condiciones iniciales

${\displaystyle \begin{array}{l}t=0\{\begin{array}{l}0=A+\frac{2\gamma g}{{\omega }_0^2}\\ g=-\gamma A+\omega B\end{array}\\ v=g\left\{\frac{2\gamma }{{\omega }_0^2}+\exp (-\gamma t)\left(\frac{1}{\omega }\left(1-\frac{2{\gamma }^2}{{\omega }_0^2}\right)\sin (\omega t)-\frac{2\gamma }{{\omega }_0^2}\cos (\omega t)\right)\right\}\\ \frac{dv}{dt}=g\exp (-\gamma t)\left(\frac{\gamma }{\omega }\sin (\omega t)+\cos (\omega t)\right)\end{array}}$

Despejamos la intensidad i de la ecuación del movimiento

${\displaystyle \begin{array}{l}i=\frac{1}{Ba}\left(mg-m\frac{dv}{dt}\right)\\ i=\frac{mg}{Ba}\left(1-\exp (-\gamma t)\left(\frac{\gamma }{\omega }\sin (\omega t)+\cos (\omega t)\right)\right)\end{array}}$

Para obtener la posición x del lado inferior de la espira integramos dx/dt=v, sabiendo que para t=0, x=0, parte del origen

${\displaystyle x=g\left\{\frac{2\gamma }{{\omega }_0^2}t+\frac{1}{\omega }\left(1-\frac{2{\gamma }^2}{{\omega }_0^2}\right){\displaystyle \underset{0}{\overset{t}{\int }}\exp (-\gamma t)}\sin (\omega t)·dt-\frac{2\gamma }{{\omega }_0^2}{\displaystyle \underset{0}{\overset{t}{\int }}\exp (-\gamma t)}\cos (\omega t)·dt\right\}}$

Integrando dos veces por partes,

${\displaystyle \begin{array}{l}{\displaystyle \int \exp (-\gamma t)\cos (\omega t)·dt=\frac{\exp (-\gamma t)}{{\omega }_0^2}}\left\{-\gamma \cos (\omega t)+\omega \sin (\omega t)\right\}\\ {\displaystyle \int \exp (-\gamma t)\sin (\omega t)·dt=-\frac{\exp (-\gamma t)}{{\omega }_0^2}}\left\{\gamma \sin (\omega t)+\omega \cos (\omega t)\right\}\end{array}}$

>> syms g w t;
>> int(exp(-g*t)*sin(w*t),t)
ans =-(exp(-g*t)*(g*sin(t*w) + w*cos(t*w)))/(g^2 + w^2)
>> int(exp(-g*t)*cos(w*t),t)
ans =-(exp(-g*t)*(g*cos(t*w) - w*sin(t*w)))/(g^2 + w^2)

obtenemos la posición x, del lado inferior de la espira en función del tiempo

${\displaystyle x=\frac{g}{{\omega }_0^2}\left\{2\gamma ·t+\exp (-\gamma t)\left(\left(\frac{4{\gamma }^2}{{\omega }_0^2}-1\right)\cos (\omega t)-\frac{\gamma }{\omega }\left(3-\frac{4{\gamma }^2}{{\omega }_0^2}\right)\sin (\omega t)\right)-\frac{4{\gamma }^2}{{\omega }_0^2}+1\right\}}$

Después de un tiempo muy grande, t→∞, la velocidad v y la intensidad i tienden a

${\displaystyle \begin{array}{l}{v}_{\infty }=\frac{2\gamma g}{{\omega }_0^2}=\frac{mgR}{B^2{a}^2}\\ i_{\infty }=\frac{mg}{Ba}\end{array}}$

Ejemplo

Fijamos los siguientes parámetros

• La masa de la espira, m=0.1 kg
• Anchura de la espira rectangular, a=0.25 m
• Autoinducción de la espira, L=8·10^-5 H

Cambiamos los valores de los parámetros

• Frecuencia propia de las oscilaciones, ω₀=10 rad/s
• Constante de amortiguamiento, γ=2 s^-1

Conocidos estos, calculamos el campo magnético $B=\frac{{\omega }_0}{a}\sqrt{mL}$ y la resistencia de la espira R=2Lγ

• Resistencia de la espira, R=3.2·10^-4 Ω
• Campo magnético aplicado, B=0.113 T

En el script definimos las funciones que nos calculan: la velocidad v, intensidad de la corriente inducida en la espira, i y posición x del lado inferior de la espira rectangular, en función del tiempo t

m=0.1; %masa
a=0.25; %ancho de la espira rectangular
L=8e-5; %autoinducción

w0=10; %frecuencia propia
gamma=2; %constante de amortiguamiento
R=2*L*gamma; %resistencia
B=w0*sqrt(m*L)/a; %campo magnético

w=sqrt(w0^2-gamma^2); %frecuencia de la oscilación amortiguada
%velocidad
v=@(t) 9.8*(2*gamma/w0^2+exp(-gamma*t).*((1-2*gamma^2/w0^2)*sin(w*t)/w-
2*gamma*cos(w*t)/w0^2));
%intensidad
i=@(t) m*9.8*(1-exp(-gamma*t).*(gamma*sin(w*t)/w+cos(w*t)))/(B*a);
%posición del lado inferior de la espira
x=@(t) 9.8*(2*gamma*t+exp(-gamma*t).*((4*gamma^2/w0^2-1)*cos(w*t)+
gamma*(4*gamma^2/w0^2-3)*sin(w*t)/w)-4*gamma^2/w0^2+1)/w0^2;
fplot(v,[0,5*2*pi/w0]) %velocidad
fplot(i,[0,5*2*pi/w0]) %intensidad
fplot(x,[0,3*2*pi/w0]) %posición
grid on
xlabel('t')
ylabel('v')
title('Amortiguadas, velocidad')

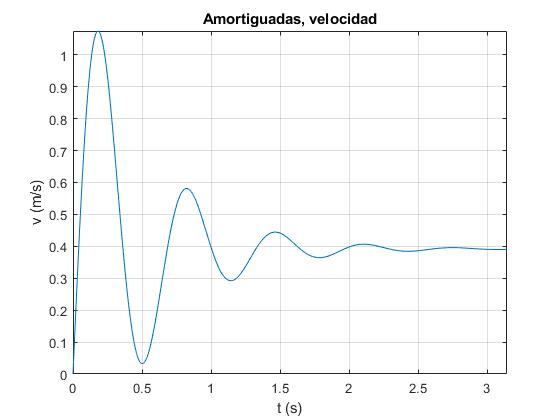
Modificamos la sentencia fplot para representar la intensidad i

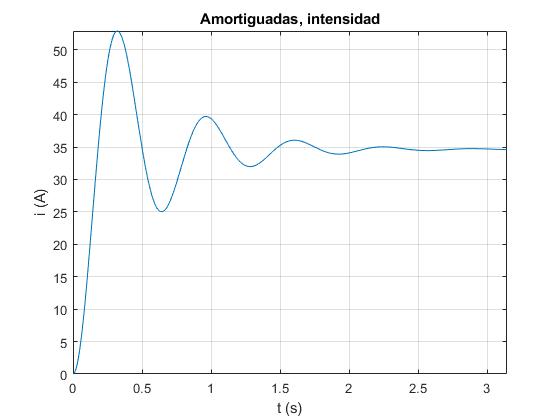
Modificamos la sentencia fplot para representar la posición x del lado inferior de la espira rectangular

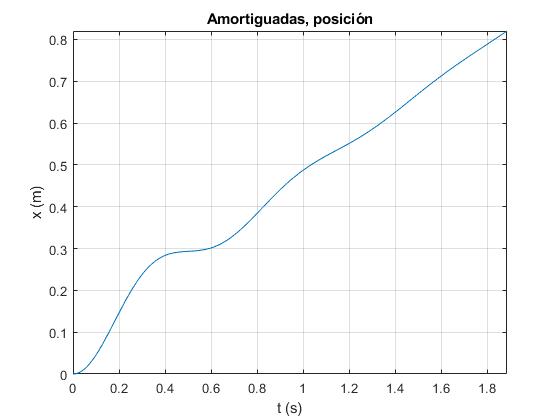
Superconductor

La resistencia de una espira hecha de un material superconductor es nula, R=0, γ=0, ω=ω₀

${\displaystyle v=\frac{g}{{\omega }_0}\sin ({\omega }_{0}t)}$

Como v=dx/dt, integramos esta ecuación diferencial, sabiendo que en el instante t=0, x=0

${\displaystyle x=\frac{g}{{\omega }_0^2}\left(1-\cos ({\omega }_{0}t)\right)}$

Obtenemos esta misma ecuación, suponiendo que en el caso de un superconductor, el flujo a través de la espira es constante, -Bax+Li=constante. En el instante t=0, x=0, i=0, por lo que i=Bax/L. Sustituyendo en la ecuación del movimiento

${\displaystyle \begin{array}{l}m\frac{dv}{dt}=mg-\frac{Ba}{L}xBa\\ \frac{d^{2}x}{d{t}^2}+{\omega }_0^{2}x=g\end{array}}$

Cuya solución es (particular más homogénea)

${\displaystyle \begin{array}{l}x=A\cos ({\omega }_{0}t)+B\sin ({\omega }_{0}t)+\frac{g}{{\omega }_0^2}\\ v=\frac{dx}{dt}={\omega }_0\left(-A\sin ({\omega }_{0}t)+B\cos ({\omega }_{0}t)\right)\\ t=0\{\begin{array}{l}0=A+\frac{g}{{\omega }_0^2}\\ 0={\omega }_{0}B\end{array}\\ x=\frac{g}{{\omega }_0^2}\left(1-\cos ({\omega }_{0}t)\right)\end{array}}$

El lado inferior de la espira oscila entre x=0 y

${\displaystyle x_{máx}=\frac{2g}{{\omega }_0^2}}$

con frecuencia angular ω₀. La intensidad varía de i=0 cuando x=0 a

${\displaystyle i_{máx}=\frac{2mg}{Ba}}$

Energías

En el instante t=0, la posición del lado inferior de la espira es x=0, parte del reposo, v=0, y la intensidad inducida i=0, por lo que la energía inicial es cero. La energía de la espira en el instante t es la suma de

• La energía cinética

${\displaystyle E_k=\frac{1}{2}m{v}^2=\frac{1}{2}m\frac{g^2}{{\omega }_0^2}{\cos }^2({\omega }_{0}t)}$

• La energía potencial

${\displaystyle E_p=-mgx=-mg\frac{g}{{\omega }_0^2}\left(1-\cos ({\omega }_{0}t)\right)}$

• La energía asociada al campo magnético en la autoinducción

${\displaystyle E_L=\frac{1}{2}L{i}^2=\frac{1}{2}L{\left(\frac{Bax}{L}\right)}^2=\frac{1}{2}m\frac{g^2}{{\omega }_0^2}{\left(1-\cos ({\omega }_{0}t)\right)}^2}$

La suma de las tres contribuciones es, E_k+E_p+E_L=0

Ejemplo

Un posible experimento para mostrar las oscilaciones de la espira superconductora R=0, sería el siguiente:

• Espira cuadrada de lado a=1 cm=10^-2 m
• Autoinducción, L=10^-8 H
• Masa, m=1.4 g=1.4·10^-3 kg
• Campo magnético perpendicular al plano de la espira, B=0.05 T. Por debajo del valor crítico 0.07 T que destruiría su estado superconductor

m=1.4e-3; %masa
a=0.01; %ancho de la espira rectangular
B=0.05; %campo magnético
L=1e-8; %autoinducción

w0=sqrt(B^2*a^2/(m*L)); %frecuencia angular
x=@(t) 9.8*(1-cos(w0*t))/w0^2;
fplot(x,[0,5*2*pi/w0]) %cinco periodos
grid on
xlabel('t (s)')
ylabel('x (m)')
title('Espira superconductora, posición')

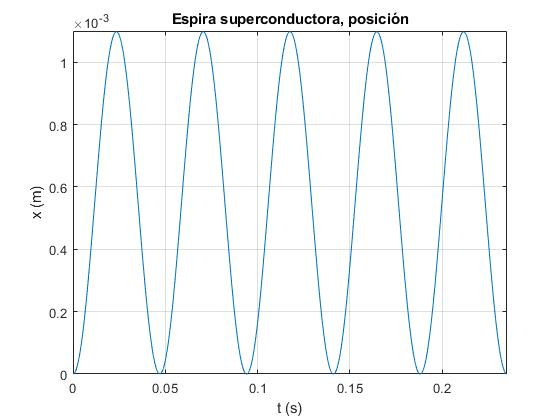
El periodo de las oscilaciones sería, 2π/ω₀=0.047 s. Su lado inferior oscilaría entre las posiciones x=0, y x_máx=0.0011 m. El lado inferior estaría en la región x>0, donde no hay campo magnético y el lado superior estaría en la región x<0, donde hay campo magnético B. La máxima intensidad que circularía por la espira, i_máx=54.9 A

Oscilaciones críticas

Cuando la resistencia aumenta, puede ocurrir que γ=ω₀.

La solución de la ecuación diferencial es

${\displaystyle \begin{array}{l}v=\exp (-\gamma t)\left(At+B\right)+\frac{2g}{\gamma }\\ \frac{dv}{dt}=\exp (-\gamma t)\left(-\gamma At+A-\gamma B\right)\end{array}}$

Donde A y B se determinan a partir de las condiciones iniciales

${\displaystyle \begin{array}{l}t=0\{\begin{array}{l}0=B+\frac{2g}{\gamma }\\ g=A-\gamma B\end{array}\\ v=\frac{2g}{\gamma }-\exp (-\gamma t)\left\{gt+\frac{2g}{\gamma }\right\}\\ \frac{dv}{dt}=g\left(\gamma t+1\right)\exp (-\gamma t)\end{array}}$

Despejamos la intensidad i de la ecuación del movimiento

${\displaystyle \begin{array}{l}i=\frac{1}{Ba}\left(mg-m\frac{dv}{dt}\right)\\ i=\frac{mg}{Ba}\left\{1-\left(\gamma t+1\right)\exp (-\gamma t)\right\}\end{array}}$

Para obtener la posición x del lado inferior de la la espira integramos dx/dt=v, sabiendo que para t=0, x=0, parte del origen

${\displaystyle x=\frac{2g}{\gamma }t-g{\displaystyle \underset{0}{\overset{t}{\int }}t\exp (-\gamma t)·dt}-\frac{2g}{\gamma }{\displaystyle \underset{0}{\overset{t}{\int }}\exp (-\gamma t)·dt}}$

Integrando por partes,

${\displaystyle {\displaystyle \underset{0}{\overset{t}{\int }}t\exp (-\gamma t)·dt}=-\frac{1}{\gamma }\left(t+\frac{1}{\gamma }\right)\exp (-\gamma t)}$

obtenemos la posición x, del lado inferior de la espira en función del tiempo.

${\displaystyle x=\frac{2g}{\gamma }t+\frac{g}{\gamma }t\exp (-\gamma t)+\frac{3g}{{\gamma }^2}\exp (-\gamma t)-\frac{3g}{{\gamma }^2}}$

Ejemplo

Cambiamos los valores de los parámetros

• Frecuencia propia de las oscilaciones, ω₀=10 rad/s
• Constante de amortiguamiento, γ=10 s^-1

Conocidos estos, calculamos el campo magnético B y la resistencia de la espira R

• Resistencia de la espira, R=0.0016 Ω
• Campo magnético aplicado, B=0.113 T

En el script definimos las funciones que nos calculan: la velocidad v, intensidad de la corriente inducida en la espira, i y posición x del lado inferior de la espira rectangular, en función del tiempo t

m=0.1; %masa
a=0.25; %ancho de la espira rectangular
L=8e-5; %autoinducción

w0=10; %frecuencia propia
gamma=w0; %constante de amortiguamiento
R=2*L*gamma; %resistencia
B=w0*sqrt(m*L)/a; %campo magnético

%velocidad
v=@(t) 9.8*(2/gamma-(t+2/gamma).*exp(-gamma*t));
%intensidad
i=@(t) m*9.8*(1-(gamma*t+1).*exp(-gamma*t))/(B*a);
%posición
x=@(t) 9.8*(2*t/gamma+t.*exp(-gamma*t)/gamma+3*(exp(-gamma*t)-1)/gamma^2);
fplot(v,[0,3*2*pi/w0]) %velocidad
grid on
xlabel('t (s)')
ylabel('v (m/s)')
title('Críticas, velocidad')

Representamos la velocidad de la espira en función del tiempo

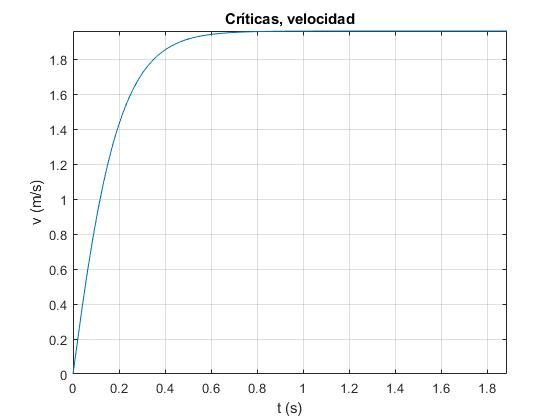
La velocidad alcanza rápidamente el valor límite constante, v_∞=g/γ. Modificamos la sentencia fplot para representar la intensidad i o la posición x del lado inferior de la espira

Oscilaciones sobreamortiguadas

Cuando la resistencia es grande, puede ocurrir que γ>ω₀.

La solución de la ecuación diferencial es

${\displaystyle \begin{array}{l}v=\exp (-\gamma t)\left(A\cosh (\omega t)+B\sinh (\omega t)\right)+\frac{2\gamma g}{{\omega }_0^2},{\omega }^2={\gamma }^2-{\omega }_0^2\\ \frac{dv}{dt}=-\gamma \exp (-\gamma t)\left(A\cosh (\omega t)+B\sinh (\omega t)\right)+\omega \exp (-\gamma t)\left(A\sinh (\omega t)+B\cosh (\omega t)\right)\end{array}}$

Donde A y B se determinan a partir de las condiciones iniciales

${\displaystyle \begin{array}{l}t=0\{\begin{array}{l}0=A+\frac{2\gamma g}{{\omega }_0^2}\\ g=-\gamma A+\omega B\end{array}\\ v=g\left\{\frac{2\gamma }{{\omega }_0^2}+\exp (-\gamma t)\left(\frac{1}{\omega }\left(1-\frac{2{\gamma }^2}{{\omega }_0^2}\right)\sinh (\omega t)-\frac{2\gamma }{{\omega }_0^2}\cosh (\omega t)\right)\right\}\\ \frac{dv}{dt}=g\exp (-\gamma t)\left(\frac{\gamma }{\omega }\sinh (\omega t)+\cosh (\omega t)\right)\end{array}}$

Despejamos la intensidad de la ecuación del movimiento

${\displaystyle \begin{array}{l}i=\frac{1}{Ba}\left(mg-m\frac{dv}{dt}\right)\\ i=\frac{mg}{Ba}\left(1-\exp (-\gamma t)\left(\frac{\gamma }{\omega }\sinh (\omega t)+\cosh (\omega t)\right)\right)\end{array}}$

Para obtener la posición x del lado inferior de la la espira integramos dx/dt=v, sabiendo que para t=0, x=0, parte del origen

${\displaystyle x=g\left\{\frac{2\gamma }{{\omega }_0^2}t+\frac{1}{\omega }\left(1-\frac{2{\gamma }^2}{{\omega }_0^2}\right){\displaystyle \underset{0}{\overset{t}{\int }}\exp (-\gamma t)}\sinh (\omega t)·dt-\frac{2\gamma }{{\omega }_0^2}{\displaystyle \underset{0}{\overset{t}{\int }}\exp (-\gamma t)}\cosh (\omega t)·dt\right\}}$

Integrando por partes

${\displaystyle \begin{array}{l}{\displaystyle \int \exp (-\gamma t)\cosh (\omega t)·dt=-\frac{\exp (-\gamma t)}{{\omega }_0^2}}\left\{\gamma \cosh (\omega t)+\omega \sinh (\omega t)\right\}\\ {\displaystyle \int \exp (-\gamma t)\sin (\omega t)·dt=-\frac{\exp (-\gamma t)}{{\omega }_0^2}}\left\{\gamma \sinh (\omega t)+\omega \cosh (\omega t)\right\}\end{array}}$

obtenemos la posición x, del lado inferior de la espira en función del tiempo.

${\displaystyle x=\frac{g}{{\omega }_0^2}\left\{2\gamma ·t+\exp (-\gamma t)\left(\left(\frac{4{\gamma }^2}{{\omega }_0^2}-1\right)\cosh (\omega t)-\frac{\gamma }{\omega }\left(3-\frac{4{\gamma }^2}{{\omega }_0^2}\right)\sinh (\omega t)\right)-\frac{4{\gamma }^2}{{\omega }_0^2}+1\right\}}$

Ejemplo

Cambiamos los valores de los parámetros

• Frecuencia propia de las oscilaciones, ω₀=10 rad/s
• Constante de amortiguamiento, γ=12 s^-1

Conocidos estos, calculamos el campo magnético B y la resistencia de la espira R

• Resistencia de la espira, R=0.0019 Ω
• Campo magnético aplicado, B=0.113 T

En el script definimos las funciones que nos calculan: la velocidad v, intensidad de la corriente inducida en la espira, i y posición x del lado inferior de la espira rectangular, en función del tiempo t

m=0.1; %masa
a=0.25; %ancho de la espira rectangular
L=8e-5; %autoinducción

w0=10; %frecuencia propia
gamma=12; %constante de amortiguamiento
R=2*L*gamma; %resistencia
B=w0*sqrt(m*L)/a; %campo magnético

w=sqrt(gamma^2-w0^2); 
%velocidad
v=@(t) 9.8*(2*gamma/w0^2+exp(-gamma*t).*((1-2*gamma^2/w0^2)*sinh(w*t)/w-
2*gamma*cosh(w*t)/w0^2));
%intensidad
i=@(t) m*9.8*(1-exp(-gamma*t).*(gamma*sinh(w*t)/w+cosh(w*t)))/(B*a);
%posición
x=@(t) 9.8*(2*gamma*t+exp(-gamma*t).*((4*gamma^2/w0^2-1)*cosh(w*t)+
gamma*(4*gamma^2/w0^2-3)*sinh(w*t)/w)-4*gamma^2/w0^2+1)/w0^2;
fplot(v,[0,3*2*pi/w0]) %velocidad
grid on
xlabel('t (s)')
ylabel('v (m/s)')
title('Sobreamortiguadas, velocidad')

Representamos la velocidad de la espira en función del tiempo

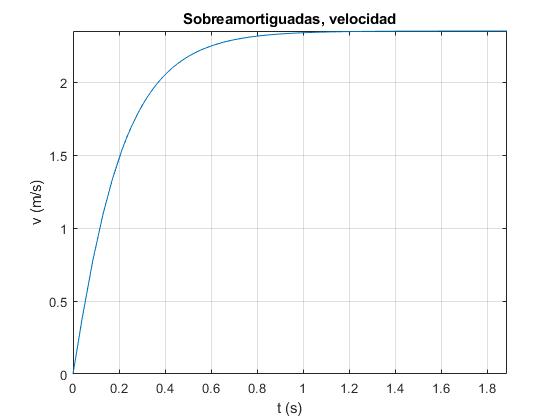
La velocidad alcanza rápidamente el valor límite constante, v_∞=2γg/ω₀². Modificamos la sentencia fplot para representar la intensidad i o la posición x del lado inferior de la espira

Estudio energético

Las energías que inteviene son:

• La energía cinética de la espira, $E_k=\frac{1}{2}m{v}^2$

• La energía potencial de la espira -mgx. El nivel cero de energía potencial se establece cuando el lado inferior de la espira está en el origen, x=0

• La energía que se acumula en forma de campo magnético en la autoinducción, $E_L=\frac{1}{2}L{i}^2$

• La energía que se pierde en la resistencia R,

${\displaystyle E_R=\underset{0}{\overset{t}{{\displaystyle \int }}}{i}^{2}Rdt}$

La energía inicial, t=0, x=0, v=0, i=0, es nula, E_i=0

La energía final es la suma

${\displaystyle E_f=\frac{1}{2}m{v}^2+\frac{1}{2}L{i}^2-mgx}$

La diferencia, es decir, la energía final, es la que se disipa en la resistencia

Comprobamos que la energía E_f en el instante t, es igual (en valor absoluto) a la energía disipada en la resistencia. Añadimos las siguientes líneas a cualquiera de los tres scripts (amortiguadas, críticas o sobreamortiguadas)

...%amortiguadas
t=0.5; %instante
Ef=m*v(t)^2/2+L*i(t)^2/2-m*9.8*x(t); %energía final
f=@(t) i(t).^2*R;
resis=integral(f,0,t); %disipada en la resistencia
disp([Ef,resis])

   -0.2388    0.2388

Actividades

Se introduce

• La constante de amortiguamiento γ en el control titulado Amortiguamiento
• El sentido del campo magnético B perpendicular al plano de la espira, hacia dentro (color azul), hacia fuera (color rosa), en el contro titulado Sentido del campo magnético

El programa interactivo ha fijado los valores de los siguientes parámetros:

• La masa de la espira, m=0.1 kg
• Anchura de la espira rectangular, a=0.25 m
• Autoinducción de la espira, L=8·10^-5 H
• Frecuencia propia de las oscilaciones, ω₀=10 rad/s

Conocidos estos, determinamos el campo magnético $B=\frac{{\omega }_0}{a}\sqrt{mL}$ y la resistencia de la espira R=2Lγ

Se suguiere al lector probar las siguintes situaciones:

• Cuando la constante de amortiguamiento γ=0, tenemos una espira hecha de un material superconductor, la resistencia R=0, y se producen las oscilaciones libres. Este es el caso más interesante
• Oscilaciones amortiguadas, γ<ω₀
• Oscilaciones críticas, γ=ω₀
• Oscilaciones sobreamortiguadas, γ>ω₀

La espira se mueva bajo la acción de su peso y de la fuerza hacia arriba, que ejerce el campo magnético sobre la corriente inducida en el lado superior de la espira. Los vectores señalan la intensidad, vector ${\widehat{u}}_t$ (color rojo), vector campo magnético $\overrightarrow{B}$, (color azul) y el vector fuerza $\overrightarrow{F_m}=i{\widehat{u}}_t\times \overrightarrow{B}a$, (color negro). La fuerza magnética es proporcional a la intensidad de la corriente inducida i en la espira

Cuando la espira sale del campo magnético, la fuerza magnética desaparece y la espira se mueve bajo la acción de su propio peso (movimiento uniformemente acelerado). Supondremos que la intensidad decrece rápidamente debido a la resistencia del circuito

Los puntos de color rojo sobre la espira representan portadores de carga positivos y señalan el sentido de la corriente inducida en la espira. Estos puntos se mueven con una velocidad proporcional a la intensidad de la corriente. En la parte derecha, se representa la intensidad (en valor absoluto) de la corriente inducida en la espira.

En la parte superior derecha, se proporcionan los datos del tiempo t en s, la posición x en cm del lado inferior de la espira y su velocidad v en cm/s

Referencias

Saslow W. M., Electromechanical implications of Faraday’s law: A problem collection. Am. J. Phys. 55 (11) November 1987, pp. 986-993.

Robert H Romer. The motion of a superconducting loop in an inhomogeneous magnetic field: the harmonic oscillator equation in an unfamiliar setting. Eur. J. Phys. 11 (1990), pp. 103-106