Modelo electromecánico

Vamos a elaborar un modelo que explique las características esenciales del movimiento del imán en un tubo metálico vertical. En este modelo sustituimos el tubo metálico que tiene un radio interior y un radio exterior, por un conjunto de espiras del mismo radio a, separadas una distancia d. El imán se mueve a lo largo del eje vertical común de las espiras. Supondremos que cada espira presenta una resistencia R al paso de la corriente inducida. En la figura, se muestran las corrientes inducidas que se generan en el tubo por delante y por detrás del imán.

No consideraremos los efectos de la autoinducción de cada espira, ni la inducción mutua entre espiras.

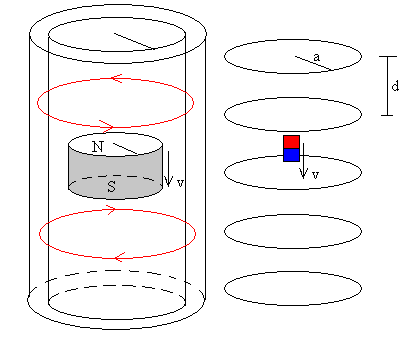
En las páginas tituladas “Demostración de la ley de Faraday”, hemos estudiado la corriente inducida producida en una espira, cuando un imán se mueve a lo largo de su eje con velocidad constante. La corriente inducida no afecta al movimiento del imán.

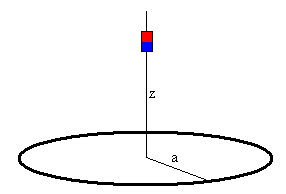
En esta página, vamos a estudiar un ejemplo algo más complicado. El imán se sitúa a cierta altura, se libera y cae bajo la acción de la gravedad hacia las espiras a lo largo de su eje. Se originan corrientes inducidas en las espiras próximas que van a modificar el movimiento del imán.

Efecto de una espira

En primer lugar, vamos a ver el efecto de una espira

Fuerzas sobre el imán

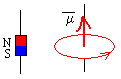
El campo magnético producido por una espira de radio a por la que circula una corriente eléctrica de intensidad I, en un punto z de su eje es

${\displaystyle B_z=\frac{{\mu }_{0}I}{2}\frac{a^2}{{\left(z^2+a^2\right)}^{3/2}}}$

Consideramos el imán como un dipolo de momento $\overrightarrow{\mu }=\mu \widehat{k}$

La energía potencial de un dipolo de momento magnético $\overrightarrow{\mu }$ en un campo magnético $\overrightarrow{B}$ que tiene la dirección del eje Z es el producto escalar

${\displaystyle U=-\overrightarrow{\mu }·\overrightarrow{B}=-\mu B_z}$

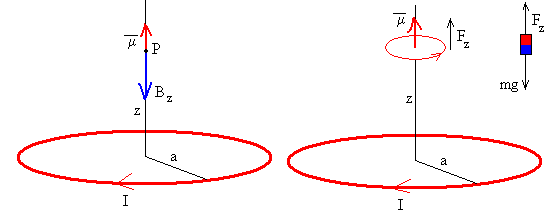
Como B es variable a lo largo del eje de la espira, el dipolo magnético experimenta una fuerza

${\displaystyle F_z=-\frac{\partial U}{\partial z}=-\frac{3\mu {\mu }_{0}I{a}^2}{2}\frac{z}{{\left(z^2+a^2\right)}^{5/2}}}$

Si la corriente I en la espira es negativa (en el sentido de las agujas del reloj) la fuerza es repulsiva (las corrientes se repelen si tienen sentido contrario y se atraen, si tienen el mismo sentido).

Aplicamos la segunda ley de Newton al movimiento del imán

${\displaystyle m\frac{d^{2}z}{d{t}^2}=-mg-\frac{3\mu {\mu }_{0}I{a}^2}{2}\frac{z}{{\left(z^2+a^2\right)}^{5/2}}}$

Ecuación del circuito (espira)

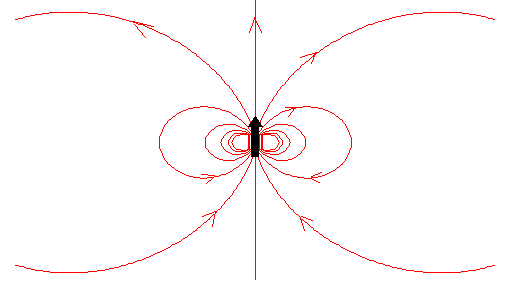
En la página, Campo magnético producido por una imán hemos supuesto que un imán se comporta como un dipolo magnético de momento μ. Las componentes del campo son

${\displaystyle \begin{array}{l}{B}_{\rho }=\frac{{\mu }_0\mu }{4\pi }\frac{3\rho z}{{\left(\sqrt{z^2+{\rho }^2}\right)}^5}\\ B_z=\frac{{\mu }_0\mu }{4\pi }\frac{2z^2-{\rho }^2}{{\left(\sqrt{z^2+{\rho }^2}\right)}^5}\end{array}}$

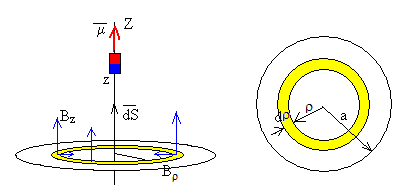
El flujo del campo producido por el imán a través de una espira de radio a es.

${\displaystyle \Phi =\underset{S}{{\displaystyle \int }}\overrightarrow{B}\cdot \overrightarrow{dS}=\underset{S}{{\displaystyle \int }}(B_{\rho }\widehat{j}+B_z\widehat{k})\cdot dS·\widehat{k}=\underset{S}{{\displaystyle \int }}{B}_z·dS}$

El elemento diferencial de superficie dS, es el área de un anillo de radio ρ y de espesor dρ, su valor es dS=2πρ·dρ

${\displaystyle \begin{array}{l}\Phi ={\displaystyle \underset{0}{\overset{a}{\int }}\frac{{\mu }_0·\mu }{4\pi }\left(\frac{3z^2}{{\left(\sqrt{{\rho }^2+z^2}\right)}^5}-\frac{1}{{\left(\sqrt{{\rho }^2+z^2}\right)}^3}\right)2\pi \rho ·d\rho }\\ \Phi =\frac{{\mu }_0\mu }{4}\left(3z^2{\displaystyle \underset{0}{\overset{a}{\int }}\frac{2\rho ·d\rho }{{\left(\sqrt{{\rho }^2+z^2}\right)}^5}-}{\displaystyle \underset{0}{\overset{a}{\int }}\frac{2\rho ·d\rho }{{\left(\sqrt{{\rho }^2+z^2}\right)}^3}}\right)=\frac{{\mu }_0\mu ·a^2}{2{\left(\sqrt{a^2+z^2}\right)}^3}\end{array}}$

Aplicando la ley de Faraday

${\displaystyle V_{\epsilon }=-\frac{d\Phi }{dt}=-\frac{d\Phi }{dz}\frac{dz}{dt}=\frac{3{\mu }_0\mu a^2}{2}\frac{z}{{\left(a^2+z^2\right)}^{5/2}}\frac{dz}{dt}}$

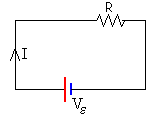
La espira tiene una resistencia R. La espira es equivalente al circuito de la figura, cuya ecuación es V_ε=IR

${\displaystyle IR=\frac{3{\mu }_0\mu a^2}{2}\frac{z}{{\left(a^2+z^2\right)}^{5/2}}\frac{dz}{dt}}$

Solución de la ecuación del movimiento

Sustituyendo la intensidad I en la ecuación del movimiento, obtenemos la ecuación diferencial

${\displaystyle m\frac{d^{2}z}{d{t}^2}=-mg-\frac{9{(\mu {\mu }_0)}^2{a}^4}{4R}\frac{z^2}{{\left(z^2+a^2\right)}^5}\frac{dz}{dt}}$

Como dz/dt<0, la fuerza que ejerce sobre el imán el campo magnético producido por la corriente inducida de la espira se opone a la velocidad, es una fuerza de frenado, pero no es de la forma λv, ya que λ no es constante.

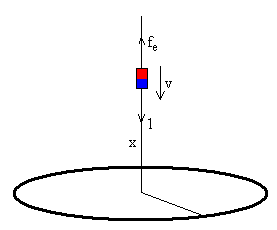
Para determinar la posición y velocidad del imán en función del tiempo, tenemos que resolver una ecuación diferencial de segundo orden por procedimientos numéricos con las siguientes condiciones iniciales: en el instante t=0, z=z₀, dz/dt=0. El imán parte del reposo desde la altura z₀.

Escribimos la ecuación diferencial en forma adimensional, definiendo las nuevas variables x y τ.

${\displaystyle z=xat=\tau \sqrt{\frac{a}{g}}}$

La ecuación diferencial en términos de las variables adimensionales x, τ se escribe.

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{\tau }^2}=-1-\frac{9{(\mu {\mu }_0)}^2}{4mR\sqrt{g{a}^7}}\frac{x^2}{{\left(x^2+1\right)}^5}\frac{dx}{d\tau }\\ \frac{d^{2}x}{d{\tau }^2}=-1-k\frac{x^2}{{\left(x^2+1\right)}^5}\frac{dx}{d\tau }\end{array}}$

En este sistema de unidades, el peso equivale a una fuerza de una unidad y la fuerza que ejerce el campo magnético producido por la corriente inducida en la espira sobre el imán es

${\displaystyle f_e=-k\frac{x^2}{{\left(x^2+1\right)}^5}\frac{dx}{d\tau }}$

Donde x es la posición del imán respecto del centro de la espira. Como vemos esta fuerza disminuye rápidamente con x, por lo que solamente hemos de considerar el  efecto de las espiras más próximas al imán.

Efecto de un conjunto de espiras

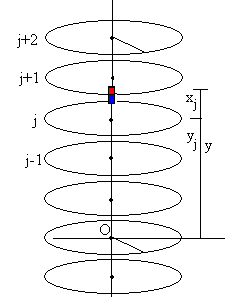
Situando el origen en O, la posición de la espira j es y_j, la posición del imán es y. La posición del imán respecto del centro de la espira es x_j=y-y_j

La resultante de las fuerzas que ejerce el campo magnético producido por las corrientes inducidas que circulan por las 2n espiras más próximas al imán por encima y por debajo valen

${\displaystyle F_e=-k{\displaystyle \sum _{j-n+1}^{j+n}\frac{{(y-y_i)}^2}{{\left({(y-y_i)}^2+1\right)}^5}\frac{dy}{d\tau }}}$

donde j es la espira más próxima que está por debajo del imán.

Todas las fuerzas tienen la misma dirección y sentido (opuesto a la velocidad) independientemente, de que la espira está por encima o por debajo del imán. Como hemos visto, esto se debe a que las corrientes inducidas en las espiras que están por debajo del imán tienen un sentido y las que están por encima, tienen sentido contrario.

• Cuando el imán se aleja de una espira, el campo magnético producido por la corriente inducida, lo atrae.

• Cuando el imán se acerca a una espira, el campo magnético producido por la corriente inducida, lo repele.

La fuerza neta sobre el imán se calcula sumando las interacciones magnéticas de todas las espiras, que como vemos es una función de la velocidad del imán y lo frenará. Cuando esta fuerza se iguala al peso, la aceleración será cero y el imán caerá con velocidad límite constante.

La ecuación del movimiento del imán es

${\displaystyle \frac{d^{2}y}{d{\tau }^2}=-1-k{\displaystyle \sum _{j-n+1}^{j+n}\frac{{(y-y_i)}^2}{{\left({(y-y_i)}^2+1\right)}^5}\frac{dy}{d\tau }}}$

Se resuelve esta ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales: en el instante adimensional τ=0, y=y₀, dy/dτ=0. El imán parte del reposo desde la posición adimensional y₀.

function a = caida_iman(t,x,k) 
    a=zeros(2,1);
    a(1)=x(2);    
    n=floor(x(1));  %x(1) posición, x(2) velocidad
    temp=0.0;
    for j=n-4:n+5
        temp=temp+(x(1)-j)^2/(1+(x(1)-j)^2)^5;
    end 
    a(2)=-1-k(1)*temp*x(2);
end

x0=zeros(1,2);
x0(1)=10; %valor inicial de x
x0(2)=0; %valor inicial de v;
tf=10; %tiempo final;
k=3; %valor del parámetro
tspan=[0 tf]; 
[t,x]=ode45(@caida_iman,tspan,x0, [],k);

plot(t,-x(:,2))  %x(2) es la velocidad
xlabel('t')
ylabel('v');
grid on
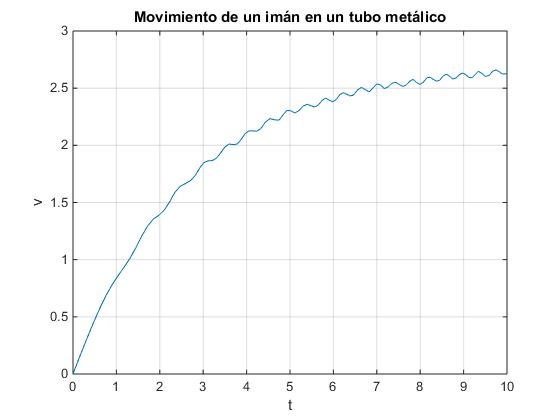
title('Movimiento de un imán en un tubo metálico')

Actividades

Se introduce

• El valor de la constante k, en el control titulado Parámetro

Se pulsa el botón titulado Nuevo

El imán parte del reposo desde la altura y₀=10. Se señala su polo norte en color rojo y el polo sur en color azul.

El tubo metálico se ha sustituido por espiras iguales situadas a una distancia de una unidad unas de las otras.

Observamos el movimiento de caída del imán, como incrementa su velocidad, pero tiende a hacia un valor medio constante a medida que transcurre el tiempo.

Al lado del imán se dibujan las fuerzas sobre el mismo:

• El peso que vale una unidad (color negro)

• La fuerza de frenado que ejercen los campos magnéticos producidos por las corrientes inducidas en las espiras sobre el imán (en color rojo).

En el programa interactivo se ha considerado suficiente el efecto de las 10 espiras más próximas al imán: cinco por encima y cinco por debajo de su posición actual.

Mediante el movimiento de puntos rojos situados en las espiras (portadores de carga positivos) se señala el sentido de la corriente inducida.

• Las corrientes inducidas en las espiras por encima del imán tiene sentido contrario a las agujas del reloj

• Las corrientes inducidas en las espiras por debajo del imán tiene el sentido de las agujas del reloj.

Observamos, que los puntos rojos se mueven más deprisa en las espiras más próximas al imán y muy poco, en las espiras más alejadas. La velocidad de los puntos rojos nos da una idea del valor de la intensidad de la corriente inducida en la espira.

En la gráfica situada a la derecha, se representa:

• En el eje horizontal el tiempo adimensional τ

• En el eje vertical, la velocidad adimensional, dy/dτ

Observamos que la velocidad media del imán tiende hacia un valor constante, aunque acelera y decelera cuando se mueve entre dos espiras consecutivas.