Campo magnético producido por el imán

En la página titulada Componentes del campo magnético producido por un solenoide, deducimos la expresión de las componentes B_ρ (radial) y B_z (a lo largo del eje) del campo magnético producido por un solenoide de diámetro 2a y longitud 2b, de n espiras por unidad de longitud recorridas por una corriente de intensidad i.

Un imán es similar a un solenoide, tal como se explica en la página titulada Campo magnético producido por un imán. Su momento magnético μ es equivalente a la corriente que pasa por todas las espiras del solenoide (2bn)i multiplicado por el área de la sección del solenoide (πa²).

μ=(2bn·i)·(πa²)

Las fórmulas que calculan las componentes B_ρ y B_z del campo producido por un imán de momento magnético μ, de radio a y longitud 2b, son

${\displaystyle \begin{array}{l}{B}_{\rho }=B_0\left\{{\alpha }_{+}C(k_{+}\mathrm{,1,1,}-1)-{\alpha }_{-}C(k_{-}\mathrm{,1,1,}-1)\right\}\\ B_z=B_0\frac{a}{a+\rho }\left\{{\beta }_{+}C(k_{+},{\gamma }^2\mathrm{,1,}\gamma )-{\beta }_{-}C(k_{-},{\gamma }^2\mathrm{,1,}\gamma )\right\}\\ B_0=\frac{{\mu }_0\mu }{2b{\left(\pi a\right)}^2}\\ z_{\pm }=z\pm b\\ k_{\pm }^2=\frac{z_{\pm }^2+{\left(a-\rho \right)}^2}{z_{\pm }^2+{\left(a+\rho \right)}^2}\\ {\alpha }_{\pm }=\frac{a}{\sqrt{z_{\pm }^2+{\left(\rho +a\right)}^2}}\\ {\beta }_{\pm }=\frac{z_{\pm }}{\sqrt{z_{\pm }^2+{\left(\rho +a\right)}^2}}\\ \gamma =\frac{a-\rho }{a+\rho }\end{array}}$

donde C es la integral elíptica generalizada, que se calcula mediante la función integral_eliptica, cuyo código MATLAB se proporciona en la página titulada Componentes del campo magnético producido por un solenoide. Así mismo, se proporciona en dicha página el código de la función calcula_campo que calcula las componentes B_ρ y B_z del campo magnético producido por un solenoide

En la página titulada, Campo magnético producido por una corriente circular en un punto fuera de su eje, mostramos que para puntos alejados de la espira, ésta se comporta como un dipolo magnético de momento μ=i(πa²),

Del mismo modo, para puntos alejados, un imán de momento magnético μ, se comporta como un dipolo. Las componentes B_ρ y B_z del campo producido por el imán son, aproximadamente

${\displaystyle \begin{array}{l}r=\sqrt{z^2+{\rho }^2}>>a,b\hfill \\ B_{\rho }=\frac{{\mu }_0\mu }{4\pi }\frac{3\rho z}{{\left(z^2+{\rho }^2\right)}^{5/2}}\hfill \\ B_z=\frac{{\mu }_0\mu }{4\pi }\frac{2z^2-{\rho }^2}{{\left(z^2+{\rho }^2\right)}^{5/2}}\hfill \end{array}}$

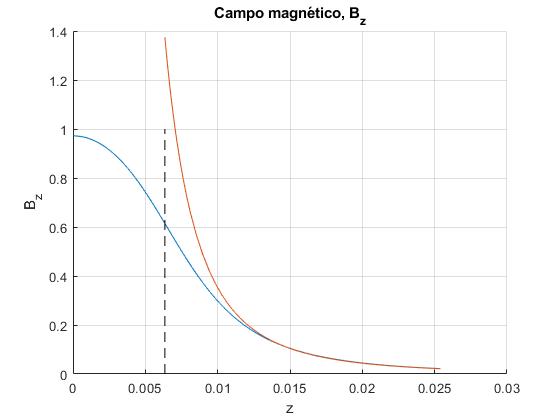
Calculamos el campo exacto y aproximado, para un imán de diámetro 2a=12.7 mm y longitud 2b=2a. El momento magnético del imán es μ=1.76 Am². Representamos la componente B_z del campo magnético producido por el imán a lo largo de su eje Z, ρ=0.

a=(12.7/2)/1000; %radio imán
b=a; %longitud del imán, 2b
mu=1.76; %momento magnético
B0=2*1e-7*mu/(b*pi*a^2);
zz=linspace(0,4*b,100);
%imán
Bz=zeros(1,length(zz));
i=1;
y=0;
for z=zz
    [B_y,B_z]=calcula_campo(a,b,y,z);
    Bz(i)=B0*B_z;
    i=i+1;
end
hold on
plot(zz,Bz)
 
%imán como dipolo
Bd_z=@(z) 1e-7*mu*(2*z.^2-y.^2)./(z.^2+y.^2).^(5/2);
fplot(Bd_z,[b,4*b])
line([b,b],[0,1],'lineStyle','--','color','k')
hold off
grid on
xlabel('z')
ylabel('B_z')
title('Campo magnético, B_z')

Hemos situado el origen en la mitad del imán, la línea a trazos señala, el extremo del imán. El cálculo exacto de B_z y su aproximación dipolar empiezan a coincidir a partir de 2b.

Consideremos el mismo imán, ahora calculamos la componente B_ρ del campo magnético producido por el imán, en la posición correspondiente al radio medio del tubo metálico es r_m=7.6 mm

a=(12.7/2)/1000; %radio imán
b=a; %longitud del imán, 2b
mu=1.76; %momento magnético
B0=2*1e-7*mu/(b*pi*a^2);
r=7.25; %radio interior del tubo
w=0.7; %espesor
rm=(r+w/2)/1000; %radio medio del tubo
 
zz=linspace(0,4*b,100);
By=zeros(1,length(zz));
Bz=zeros(1,length(zz));
i=1;
y=rm;
for z=zz
    [B_y,B_z]=calcula_campo(a,b,y,z);
    By(i)=B0*B_y;
    i=i+1;
end
hold on
plot(zz,By)
 
%imán como dipolo
Bd_y=@(z) 1e-7*mu*3*(y.*z)./(z.^2+y.^2).^(5/2);
fplot(Bd_y,[b,5*b])
line([a,a],[0,0.3],'lineStyle','--','color','k')
line([rm,rm],[0,0.3],'lineStyle','--','color','r')
hold off
grid on
xlabel('\rho')
ylabel('B_\rho')
title('Campo magnético, B_\rho')

En esta posición, el cálculo exacto y su aproximación dipolar difieren. La línea a trazos de color negro señala el radio del imán a y la línea a trazos de color rojo, el radio medio del tubo r_m.

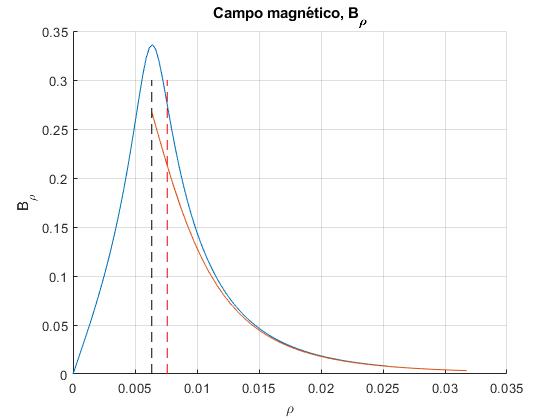
Ambas descripciones difieren aún más cuando la longitud del imán cilíndrico es mayor que su diámetro, se sugiere al lector probar b=3a, la longitud del imán es el triple que su diámetro.

Fuerzas sobre el imán

Uno de los experimentos que más llaman la atención a los estudiantes es el movimiento vertical de un imán en el interior de un tubo hecho de un material conductor (aluminio). Es una impresionante demostración a la ley de Faraday. Las pequeñas masas de los imanes y sus grandes momentos magnéticos hacen que la caída del imán se produzca a velocidad constante muy pequeña, por lo que tarda mucho tiempo en salir del tubo en comparación con la caída libre desde la misma altura.

Sea un tubo muy largo (en comparación con la longitud del imán) hecho de un material de conductividad σ, de radio interior r, de radio exterior r+w, w es el espesor, o de radio medio r_m=r+w/2. Situamos el origen en el extremo superior del tubo y el eje Z apuntando hacia abajo. Supongamos que un instante dado t, la posición del imán es z

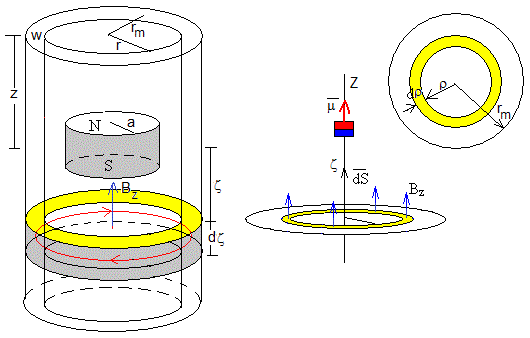
Consideremos, una espira circular dentro del tubo de radio r_m (en color rojo), que dista ζ del centro del imán. El flujo del campo magnético producido por el imán a través de la espira se debe solamente a su componente B_z

${\displaystyle \Phi (\zeta )={\displaystyle \int \overrightarrow{B}·\overrightarrow{dS}={\displaystyle \int \left(B_{\rho }\widehat{\rho }+B_z\widehat{k}\right)·dS\widehat{k}=}}{\displaystyle \underset{o}{\overset{r_m}{\int }}{B}_z(\zeta )2\pi \rho ·d}\rho }$

La fem producida en la espira, de acuerdo con la ley de Faraday, es la derivada del flujo, cambiada de signo

${\displaystyle V_{\epsilon }=-\frac{d\Phi (\zeta )}{dt}}$

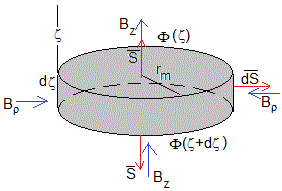
Consideremos la superficie cilíndrica de radio r_m y altura dζ, el flujo del campo magnético a través de la superficie cerrada es nulo, de acuerdo con la ley de Gauss para el campo magnético

${\displaystyle {\displaystyle \oint \overrightarrow{B}·\overrightarrow{dS}=0}}$

• El flujo a través de la base inferior, Φ(ζ+dζ), es negativo (el vector campo y el vector superficie son de signos contrarios)

• El flujo a través de la base superior, Φ(ζ), es positivo (el vector campo y el vector superficie son del mismo signo), es mayor, ya que está más cerca del imán y el módulo del campo B_z es más grande

• El flujo a través de la superficie lateral, B_ρ(2πr_mdζ), que es negativo, (el vector campo y el vector superficie son de signos contrarios).

dΦ=Φ(ζ+dζ)-Φ(ζ)=-B_ρ(2πr_mdζ)

La fem V_ε se expresa

${\displaystyle V_{\epsilon }=B_{\rho }2\pi r_m\frac{d\zeta }{dt}=B_{\rho }2\pi r_{m}v}$

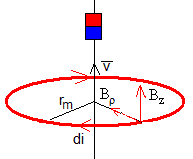
Alternativamente, desde el punto de vista del observador vinculado al imán, la espira se mueve (hacia arriba) en el seno del campo magnético producido por el imán. Aplicamos la exprersión de la fem

${\displaystyle V_{\epsilon }={{{\displaystyle \oint }}^{\text{}}}^{\text{}}(\overrightarrow{v}\times \overrightarrow{B})·\overrightarrow{dl}={\displaystyle \oint \left(v{B}_{\rho }\sin 90\right)}dl·\cos 0=v{B}_{\rho }2\pi r_m}$

La componente B_z del campo es paralela a la velocidad, por lo que no contribuye a la fem. La dirección del producto vectorial es tangente a la circunferencia de radio r_m y la componente del campo B_ρ es constante en todos los puntos de la circunferencia, por lo que la integral es inmediata. Finalmente, el sentido de la corriente inducida es el mismo que el producto vectorial y está señalado en la figura.

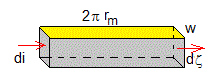
Consideremos un anillo de radio medio r_m, anchura w y altura dζ. La resistencia del anillo es (resistividad×longitud/sección)

${\displaystyle R=\frac{1}{\sigma }\frac{2\pi r_m}{w·d\zeta }}$

La intensidad de la corriente inducida es di=V_ε/R, en el sentido indicado en la figura (más arriba)

${\displaystyle di=B_{\rho }v·\sigma w·d\zeta }$

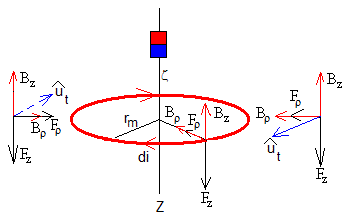
La fuerza que ejerce un campo magnético sobre una porción dl de conductor por el que circula una corriente de intensidad I es

${\displaystyle \overrightarrow{dF}=I({\widehat{u}}_t\times \overrightarrow{B})dl}$

• La componente B_z del campo magnético producido por el imán, ejerce una fuerza sobre la espira de radio r_m cuya dirección es radial.

• La componente B_ρ del campo magnético producido por el imán, ejerce una fuerza sobre la espira de radio cuya dirección es vertical

La fuerza resultante sobre la espira es vertical, anulándose por simetría en la dirección radial. El módulo de la fuerza es dF_z=di(1·B_ρ·sin90)2πr_m y su sentido es hacia abajo, tal como se indica en la figura. Por la tercera ley de Newton, la fuerza que ejercen las corrientes inducidas sobre el imán es vertical, hacia arriba, de sentido contrario a su peso

${\displaystyle d{F}_z=\left(2\pi r_m\sigma w{B}_{\rho }^2(\zeta ,r_m)d\zeta \right)v}$

Si la posición del centro del imán es z, integramos entre -z y L-z, para un tubo de longitud L. En la práctica, los tubos son muy largos, del orden de 1.5 m y podemos poner ∞ al límite superior de la integral

${\displaystyle F_z=\left(2\pi r_m\sigma w{\displaystyle \underset{-z}{\overset{L-z}{\int }}{B}_{\rho }^2(\zeta ,r_m)}·d\zeta \right)v}$

Velocidad límite

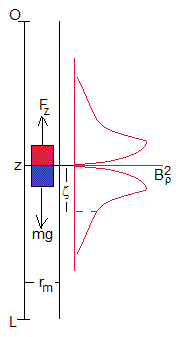
La fuerza F_z que ejercen las corrientes inducidas en el tubo sobre el imán, es proporcional a la velocidad v del imán y de sentido contrario a ésta

La fuerza F_z va creciendo hasta que se iguala al peso, mg, la fuerza neta sobre el imán tiende a cero, la velocidad límite final v_∞ se va haciendo constante.

${\displaystyle v_{\infty }=\frac{mg}{2\pi r_m\sigma w{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{B}_{\rho }^2(\zeta ,r_m)}·d\zeta }}$

La función integrando $B_{\rho }^2(\zeta ,r_m)$, es simétrica se extiende teóricamente desde -∞ a +∞, pero decae rápidamente cuando nos alejamos del imán, por tanto hay que establecer un límite δ a partir del cual consideramos que la función es prácticamente cero. Por otra parte, la integral no tiene solución analítica, tendremos que seleccionar un procedimiento numérico, Simpson (1/3), para obtener su valor numérico.

function suma=simpson(f,x0,xf,n)
%n número par de intervalos, n+1 número de puntos en el vector    
    x=linspace(x0,xf,n+1);   
    h=x(2)-x(1);
    suma=f(x(1))+f(x(n+1));
    for i=2:2:n
        suma=suma+4*f(x(i));
    end
    for i=3:2:n-1
        suma=suma+2*f(x(i));
    end
    suma=suma*h/3;
end

Al procedimiento se le pasa la función f a integrar, el límite inferior x0 el límite superior xf y el número n (par) de intervalos.

Ejemplo

• radio del imán, a=12.7/2 mm
• longitud del imán, 2b=2a=12.7 mm
• masa del imán, m=12.1 g
• momento magnético del imán, μ=1.76 Am²
• radio interior del tubo, r=7.25 mm
• espesor del tubo, w=0.7 mm
• radio medio del tubo, r_m=r+w/2=7.6 mm
• conductividad del material conductor, σ=56·10⁶ S/m

a=(12.7/2)/1000; %radio imán
b=a; %longitud del imán, 2b
m=12.1/1000; %masa
mu=1.76; %momemto magnético
r=7.25/1000; %radio interior del tubo
w=0.7/1000; %espesor
rm=r+w/2; %radio medio
sigma=56.0e6; %conductividad

B0=2*1e-7*mu/(b*pi*a^2);
zz=linspace(0,5*b,100);
By2=zeros(1,length(zz));
i=1;
y=rm;
for z=zz
    [B_y,B_z]=calcula_campo(a,b,y,z);
    By2(i)=(B0*B_y)^2;
    i=i+1;
end
hold on
plot(zz,By2)
line([b,b],[0,0.1],'lineStyle','--','color','k')
grid on
xlabel('z')
ylabel('B_\rho^2')
title('Cuadrado de la componente B_\rho')

%velocidad límite
By2=@(z) calcula_campo(a,b,rm,z).^2*B0^2;
v_inf=m*9.8/(2*pi*rm*sigma*w*2*simpson(By2, 0,5*b,200));
disp(v_inf)

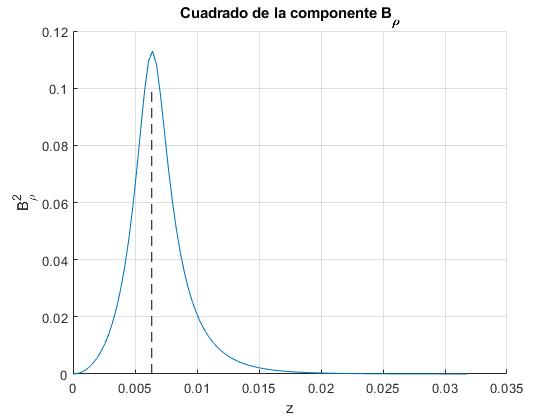
La representación gráfica del cuadrado de B_ρ nos dice que se trata de una función simétrica, que se hace prácticamente cero para z mayores que 3b, la línea a trazos marca el extremo del imán z=b. Por lo que estableceremos como límite superior de la integral δ=5b (infinito)

La velocidad límite constante v_∞, es

0.0658

Movimiento vertical del imán en el interior del tubo

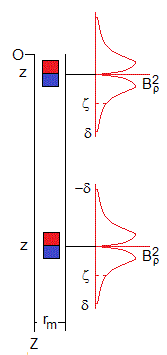
Sobre un imán de masa m actúa el peso mg y la fuerza F_z que ejercen las corrientes inducidas en el tubo sobre el imán, proporcional a la velocidad v del imán y de sentido contrario a ésta. La ecuación diferencial del movimiento es

${\displaystyle \frac{d^{2}z}{d{t}^2}=g-\left(\frac{2\pi r_m\sigma w}{m}{\displaystyle \underset{-z}{\overset{\infty }{\int }}{B}_{\rho }^2(\zeta ,r_m)d\zeta }\right)\frac{dz}{dt}}$

que resolveremos por procedimiento numéricos con las siguientes condiciones iniciales: en el instante t=0, z=0, dz/dt=0. Parte del reposo desde el extremo superior del tubo

El principal problema que se presenta es el cálculo de la integral cuyos límites dependen de la posición z del imán. Como apreciamos en la figura,

• Cuando el imán se encuentra cerca de la posición inicial, z<δ, los límites de integración serán, -z y δ

• Cuando se encuentra en una posición intermedia, z>δ, los límites de integración serán -δ y δ

Modificamos el procedimiento simpson para que refleje los nuevos límites de integración dependiendo de la posición z del imán.

function suma=simpson_1(f, z, delta, n)
%n número par de intervalos, n+1 número de puntos en el vector    
    x0=-delta;    
    if z<delta
        x0=-z;
    end
    x=linspace(x0,delta,n+1);   
    h=x(2)-x(1);
    suma=f(x(1))+f(x(n+1));
    for i=2:2:n
        suma=suma+4*f(x(i));
    end
    for i=3:2:n-1
        suma=suma+2*f(x(i));
    end
        suma=suma*h/3;
end

Ejemplo

Sea un tubo suficientemente largo de

• radio interior, r=7.25 mm
• espesor, w=0.7 mm
• radio medio, r_m=r+w/2=7.6 mm
• conductividad del material conductor, σ=56·10⁶ S/m

Dejamos caer por el extremo superior del tubo en posición vertical imanes cuyo diámetro 2a=12.7 mm y cuyas longitudes 2b, masas m y momentos magnéticos μ, se especifican en la siguiente tabla

Representamos la velocidad v de cada uno de los imanes en función del tiempo t

a=(12.7/2)/1000; %radio imán
m=[12.1, 17.9,23.8,36.4,48.2,12.9]/1000; %masas
mu=[1.76,2.36,3.23,5.00, 6.37,1.17]; %momemto magnéticoss
r=7.25/1000; %radio interior del tubo
w=0.7/1000; %espesor
rm=r+w/2; %radio medio
sigma=56.0e6; %conductividad 

hold on
kk=[1,1.5,2,3,4,1]; %relación b/a
v_inf=zeros(1,length(kk)); %velocidad límite
i=1;
for k=kk
    b=k*a; %longitud del imán, 2b
    B0=2*1e-7*mu(i)/(b*pi*a^2);
    delta=5*b; %límite de integración
    cte=2*pi*rm*sigma*w/m(i);
    By2=@(z) calcula_campo(a,b,rm,z)^2*B0^2;
    kr=@(z) simpson_1(By2, z, delta, 200)*cte;
    fg=@(t,x)[x(2); 9.8-kr(x(1))*x(2)];
    [t,x]=ode45(fg,[0,0.2],[0,0]);
    plot(t,x(:,2))
    den=2*simpson(By2, 0,delta,200);  %dos veces de 0 a infinito, simétrica
    v_inf(i)=9.8/(cte*den); %velocidad final constante
    i=i+1;
end
hold off
grid on
legend('1','2','3','4','5','6', 'location','best')
xlabel('t')
ylabel('v');
title('Velocidad')
disp(['b/a| ','masa(g)| ','m. magnético| ','v. final(cm/s)'])
disp([kk',(m')*1000,mu',(v_inf')*100])

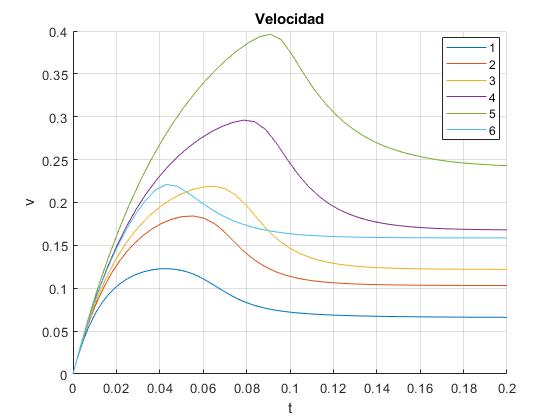
Las velocidades límite constante de cada imán v_∞, son

     b/a|  masa(g)| m. magnético| v. final(cm/s)
    1.0000   12.1000    1.7600    6.5776
    1.5000   17.9000    2.3600   10.3032
    2.0000   23.8000    3.2300   12.1915
    3.0000   36.4000    5.0000   16.7724
    4.0000   48.2000    6.3700   24.0367
    1.0000   12.9000    1.1700   15.8681

En el instante t=0.2 s las velocidades de los imanes son casi constantes. Los imanes se han desplazado muy poco a lo largo del tubo, entre 1.6 y 5.5 cm. Estos datos los proporciona el último elemento del vector posición, x(end,1)

    0.0162
    0.024
    0.0293
    0.0402
    0.0548
    0.0326

Actividades

Se introduce

• La longitud del imán, 2b en múltipos del diámetro 2a del imán en el control titulado Longitud b/a
• La masa del imán, m en g, en el control titulado Masa
• El momento magnético del imán, μ en Am², en el control titulado Momento

El programa interactivo ha fijado los siguientes parámetros:

• El radio del imán, a=12.7/2 mm
• El radio interior del tubo, r=7.25 mm
• El espesor del tubo, w=0.7 mm
• El radio medio del tubo, r_m=r+w/2=7.6 mm
• La conductividad del material del tubo, σ=56·10⁶ S/m

Por ejemplo, dejamos caer por el extremo superior del tubo en posición vertical imanes cuyas longitudes 2b, masas m y momentos magnéticos μ se especifican en la siguiente tabla

En la parte izquierda, se representa el tubo metálico y el imán a escala. En la parte derecha, la velocidad del imán en función del tiempo. En la parte superior, se proporcionan los datos de: el tiempo t, la posición z en cm y la velocidad v en cm/s del imán

Se dibujan las fuerzas sobre el imán, el peso mg un vector de longitud constante y la fuerza F_z que ejercen las corrientes inducidas en el tubo sobre el imán, que va creciendo hasta que se hace aproximadamente igual al peso. La velocidad del imán es aproximadamente constante e igual a la límite v_∞

Aproximación dipolar

En este apartado vamos a calcular la velocidad límite v_∞ utilizando la aproximación dipolar de la componente B_ρ del campo magnético producido por el imán

${\displaystyle \begin{array}{l}{B}_{\rho }=\frac{{\mu }_0\mu }{4\pi }\frac{3r_m\zeta }{{\left({\zeta }^2+r_m^2\right)}^{5/2}}\\ v_{\infty }=\frac{8\pi mg}{9r_m^3\sigma w{\left({\mu }_0\mu \right)}^2{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\frac{{\zeta }^2}{{\left({\zeta }^2+r_m^2\right)}^5}d\zeta }}\end{array}}$

Queda por resolver la integral definida. Utilizando notación tradicional, llamamos, z a ζ y a a r_m. Primero, integramos por partes

${\displaystyle {\displaystyle \int \frac{z^2}{{\left(a^2+z^2\right)}^5}dz}=\frac{-z}{8{\left(a^2+z^2\right)}^5}+\frac{1}{8}{\displaystyle \int \frac{dz}{{\left(a^2+z^2\right)}^4}}}$

Hacemos el cambio de variable

z=a·tanθ, dz=a·dθ/cos²θ

${\displaystyle \frac{1}{8}{\displaystyle \int \frac{dz}{{\left(a^2+z^2\right)}^4}}=\frac{1}{8a^7}{\displaystyle \int {\cos }^6·d\theta }}$

Empleamos la relación trigonométrica

${\displaystyle {\cos }^2\theta =\frac{1+\cos 2\theta }{2}}$

La integral se convierte en

${\displaystyle \begin{array}{l}\frac{1}{8}{\displaystyle \int \frac{dz}{{(a^2+z^2)}^4}}=\frac{1}{8a^7}{\displaystyle \int {\cos }^6·d\theta }=\frac{1}{64a^7}{\displaystyle \int (1+{\cos }^{3}2\theta +3{\cos }^{2}2\theta +3\cos 2\theta )d\theta }\\ {\displaystyle \int {\cos }^{2}2\theta ·d\theta ={\displaystyle \int \frac{1+\cos 4\theta }{2}}}d\theta =\frac{1}{2}\theta +\frac{1}{8}\sin 4\theta \\ {\displaystyle \int {\cos }^{3}2\theta ·d\theta ={\displaystyle \int (1-{\sin }^{2}2\theta )·d\theta =}}\frac{1}{2}\text{sin2}\theta -\frac{1}{6}{\sin }^{3}2\theta \end{array}}$

El resultado final es

${\displaystyle \frac{1}{8}{\displaystyle \int \frac{dz}{{\left(a^2+z^2\right)}^4}}=\frac{1}{8a^7}{\displaystyle \int {\cos }^6·d\theta }=\frac{1}{64a^7}\left(\frac{5}{2}\theta +2\sin 2\theta +\frac{3}{8}\sin 4\theta -\frac{1}{6}{\sin }^{3}2\theta \right)}$

Ahora calculamos la integral definida

${\displaystyle \begin{array}{l}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\frac{z^2}{{\left(a^2+z^2\right)}^5}dz}={\frac{-z}{8{\left(a^2+z^2\right)}^5}|}_{-\infty }^{\infty }+{\frac{1}{64a^7}\left(\frac{5}{2}\theta +2\sin 2\theta +\frac{3}{8}\sin 4\theta -\frac{1}{6}{\sin }^{3}2\theta \right)|}_{-\pi /2}^{\pi /2}=\\ \frac{1}{64a^7}\frac{5}{2}\left(\frac{\pi }{2}-\frac{-\pi }{2}\right)=\frac{5\pi }{128a^7}\end{array}}$

Recuérdese que al hacer el cambio de variable z=a·tanθ,  los límites de integración cambian de z=-∞, z=+∞, a θ=-π/2, θ=+π/2.

La velocidad v_∞ límite constante vale entonces.

${\displaystyle v_{\infty }=\frac{8\pi mg}{9r_m^3\sigma w{\left({\mu }_0\mu \right)}^2\frac{5\pi }{128r_m^7}}=\frac{1024(mg)r_m^4}{45\sigma w{\left({\mu }_0\mu \right)}^2}}$

Ejemplo

• Imán de masa m=12.1 g y de momento magnético μ=1.76 A·m²

• El tubo tiene un espesor, w=0.7 mm, un radio medio, r_m=r+w/2=7.6 mm y la conductividad del material conductor es, σ=56·10⁶ S/m

• Teniendo en cuenta que μ₀=4π·10^-7 en unidades S.I.

Obtenemos v_∞=4.69 cm/s, frente al valor 6.58 cm/s que nos da un cálculo más exacto

Referencias

Norman Derby, Stanislaw Olbert. Cylindrical magnets and ideal solenoids. Am. J. Phys. 78 (3) March 2010, pp. 229-235