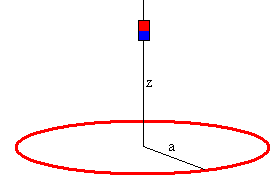
Fuerzas sobre el imán

El campo magnético producido por una espira de radio a por la que circula una corriente eléctrica de intensidad I, en un punto z de su eje es

${\displaystyle B_z=\frac{{\mu }_{0}I}{2}\frac{a^2}{{\left(z^2+a^2\right)}^{3/2}}}$

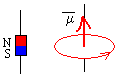
Consideramos el imán como un dipolo de momento $\overrightarrow{\mu }=\mu \widehat{k}$

La energía potencial de un dipolo de momento magnético $\overrightarrow{\mu }$ en un campo magnético $\overrightarrow{B}$ que tiene la dirección del eje Z es el producto escalar

${\displaystyle U=-\overrightarrow{\mu }·\overrightarrow{B}=-\mu B_z}$

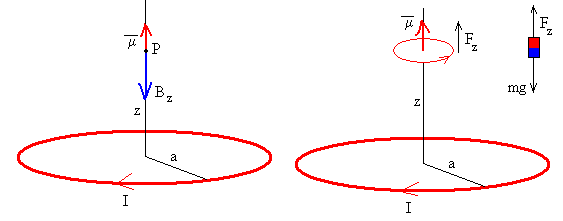
Como B es variable a lo largo del eje de la espira, el dipolo magnético experimenta una fuerza

${\displaystyle F_z=-\frac{\partial U}{\partial z}=-\frac{3\mu {\mu }_{0}I{a}^2}{2}\frac{z}{{\left(z^2+a^2\right)}^{5/2}}}$

Si la corriente I en la espira es negativa (en el sentido de las agujas del reloj) la fuerza es repulsiva (las corrientes se repelen si tienen sentido contrario y se atraen, si tienen el mismo sentido).

Aplicamos la segunda ley de Newton al movimiento del imán

${\displaystyle m\frac{d^{2}z}{d{t}^2}=-mg-\frac{3\mu {\mu }_{0}I{a}^2}{2}\frac{z}{{\left(z^2+a^2\right)}^{5/2}}}$

Ecuación del circuito (espira)

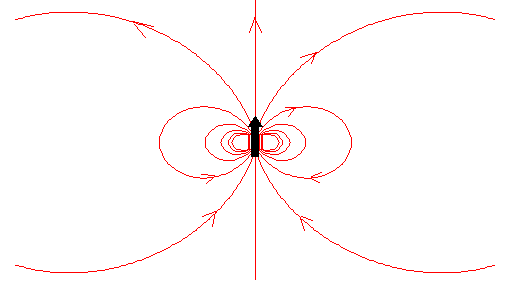
En la página, Campo magnético producido por una imán hemos supuesto que un imán se comporta como un dipolo magnético de momento μ. Las componentes del campo son

${\displaystyle \begin{array}{l}{B}_{\rho }=\frac{{\mu }_0\mu }{4\pi }\frac{3\rho z}{{\left({\rho }^2+z^2\right)}^{5/2}}\hfill \\ B_z=\frac{{\mu }_0\mu }{4\pi }\frac{2z^2-{\rho }^2}{{\left({\rho }^2+z^2\right)}^{5/2}}=\frac{{\mu }_0\mu }{4\pi }\left\{\frac{3z^2}{{\left({\rho }^2+z^2\right)}^{5/2}}-\frac{1}{{\left({\rho }^2+z^2\right)}^{3/2}}\right\}\hfill \end{array}}$

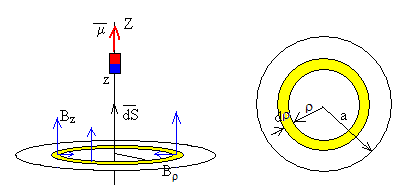
El flujo del campo producido por el imán a través de una espira de radio a es.

${\displaystyle \Phi =\underset{S}{{\displaystyle \int }}\overrightarrow{B}\cdot \overrightarrow{dS}=\underset{S}{{\displaystyle \int }}(B_{\rho }\widehat{j}+B_z\widehat{k})\cdot dS·\widehat{k}=\underset{S}{{\displaystyle \int }}{B}_z·dS}$

El elemento diferencial de superficie dS, es el área de un anillo de radio ρ y de espesor dρ, su valor es dS=2πρ·dρ

${\displaystyle \begin{array}{l}\Phi ={\displaystyle \underset{0}{\overset{b}{\int }}\frac{{\mu }_0·\mu }{4\pi }\left(\frac{3z^2}{{\left(\sqrt{{\rho }^2+z^2}\right)}^5}-\frac{1}{{\left(\sqrt{{\rho }^2+z^2}\right)}^3}\right)2\pi \rho ·d\rho }\\ \Phi =\frac{{\mu }_0\mu }{4}\left(3z^2{\displaystyle \underset{0}{\overset{b}{\int }}\frac{2\rho ·d\rho }{{\left(\sqrt{{\rho }^2+z^2}\right)}^5}-}{\displaystyle \underset{0}{\overset{b}{\int }}\frac{2\rho ·d\rho }{{\left(\sqrt{{\rho }^2+z^2}\right)}^3}}\right)=\frac{{\mu }_0\mu ·a^2}{2{\left(\sqrt{a^2+z^2}\right)}^3}\end{array}}$

Aplicando la ley de Faraday

${\displaystyle V_{\epsilon }=-\frac{d\Phi }{dt}=-\frac{d\Phi }{dz}\frac{dz}{dt}=\frac{3{\mu }_0\mu a^2}{2}\frac{z}{{\left(a^2+z^2\right)}^{5/2}}\frac{dz}{dt}}$

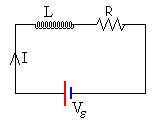
La espira tiene una resistencia R y una autoinducción L. La espira es equivalente al circuito de la figura, cuya ecuación es

${\displaystyle V_{\epsilon }-L\frac{dI}{dt}=IR}$

Recuérdese que la autoinducción actúa como una batería que se opone a los cambios en la corriente I de la espira

${\displaystyle L\frac{dI}{dt}+IR=\frac{3{\mu }_0\mu a^2}{2}\frac{z}{{\left(a^2+z^2\right)}^{5/2}}\frac{dz}{dt}}$

Balance energético

Las energías del sistema formado por la espira y el imán son:

• Energía potencial del imán, (situando el nivel cero en el origen) es mgz

• Energía cinética, $\frac{1}{2}m{v}^2$

• Energía del campo magnético producido por la espira, $\frac{1}{2}L{I}^2$

• Energía por unidad de tiempo disipada en la resistencia, I²R

Se deberá cumplir que

${\displaystyle \frac{d}{dt}\left(mgz+\frac{1}{2}m{v}^2+\frac{1}{2}L{I}^2\right)=-I^{2}R}$

Si la espira es un superconductor R=0, la suma de las tres clases de energía permanece constante.

Solución de las ecuaciones del movimiento

Para determinar el movimiento del imán tenemos que resolver un sistema de dos ecuaciones diferenciales acopladas, con las condiciones iniciales siguientes: en el instante t=0, la posición del imán es z₀, su velocidad inicial es dz/dt=v₀ y la intensidad inicial de la corriente en la espira es I₀.

${\displaystyle \begin{array}{l}m\frac{d^{2}z}{d{t}^2}=-mg-\frac{3\mu {\mu }_{0}I{a}^2}{2}\frac{z}{{\left(z^2+a^2\right)}^{5/2}}\\ L\frac{dI}{dt}+IR=\frac{3{\mu }_0\mu a^2}{2}\frac{z}{{\left(a^2+z^2\right)}^{5/2}}\frac{dz}{dt}\end{array}}$

Escribimos las ecuaciones diferenciales en forma adimensional, definiendo las nuevas variables x, τ e i.

${\displaystyle z=xat=\tau \sqrt{\frac{a}{g}}I=\frac{mg{a}^2}{{\mu }_0\mu }i}$

El sistema de dos ecuaciones diferenciales en términos de las variables adimensionales x, τ e i, se escribe.

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{\tau }^2}=-1-\frac{3}{2}\frac{x}{{(x^2+1)}^{5/2}}i\\ \frac{di}{d\tau }+\frac{R}{L}\sqrt{\frac{a}{g}}i=\frac{{(\mu {\mu }_0)}^2}{mg{a}^{3}L}\frac{3}{2}\frac{x}{{\left(x^2+1\right)}^{5/2}}\frac{dx}{d\tau }\end{array}}$

Definimos los parámetros α y β

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{\tau }^2}=-1-\frac{3}{2}\frac{x}{{\left(x^2+1\right)}^{5/2}}i\\ \frac{di}{d\tau }=-\alpha i+\frac{3\beta }{2}\frac{x}{{\left(x^2+1\right)}^{5/2}}\frac{dx}{d\tau }\\ \alpha =\frac{R}{L}\sqrt{\frac{a}{g}}\beta =\frac{{(\mu {\mu }_0)}^2}{mg{a}^{3}L}\end{array}}$

El programa interactivo que viene a continuación, resuelve el sistema de dos ecuaciones diferenciales por el procedimiento de Runge-Kutta, con las siguientes condiciones iniciales, en el instante τ=0, la posición inicial del imán es x₀, parte del reposo, su velocidad inicial dx/dτ=0, la intensidad inicial en la espira i₀=0.

En función de las variables adimensionales x, τ e i, los distintos tipos de energía se escriben:

• Energía potencial gravitatoria

mgz=-(mga)x

• Energía cinética

${\displaystyle \frac{1}{2}m{\left(\frac{dz}{dt}\right)}^2=(mga)\frac{1}{2}{\left(\frac{dx}{d\tau }\right)}^2}$

• Energía magnética

${\displaystyle \frac{1}{2}L{I}^2=\frac{1}{2}L{\left(\frac{mg{a}^2}{{\mu }_0\mu }\right)}^2{i}^2=(mga)\frac{1}{2}\frac{i^2}{\beta }}$

function a = caida_iman_1(t,x,k) 
    a=zeros(3,1);
    a(1)=x(2);    
%k(1) es alfa y k(2) es beta
%x(1) es posición, x(2) es velocidad y x(3) es intensidad
    a(2)=-1-1.5*x(1)*x(3)/(1+x(1)^2)^(5/2);
	a(3)=-k(1)*x(3)+1.5*k(2)*x(1)*x(2)/(1+x(1)^2)^(5/2);
end

x0=zeros(1,3);
x0(1)=4; %valor inicial de x
x0(2)=0; %valor inicial de v;
x0(3)=0; %intensidad inicial en la espira
tf=10; %tiempo final;
k=[0 35]; %valor de los parámetros alfa y beta
tspan=[0 tf]; 
[t,x]=ode45(@caida_iman_1,tspan,x0, [],k);

plot(t,x(:,1))  %posición en función del tiempo
xlabel('t')
ylabel('x');
grid on
title('Movimiento de un imán')

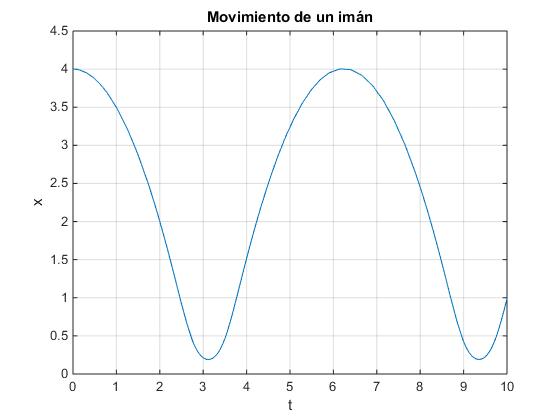
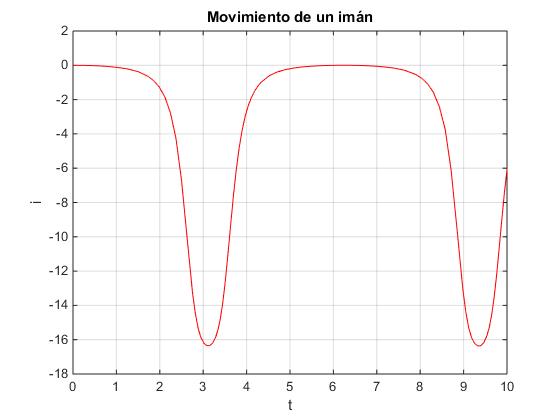
Para representar la intensidad modificamos en el script la sentencia plot

....
plot(t,x(:,3),'r')  %intensidad en función del tiempo
ylabel('i');
...

Actividades

• Establecemos la posición inicial, x₀=4.

• El radio de la espira se ha fijado en, a=1

Se introduce

• El valor del parámetro α, actuando en el control titulado Alfa. Para un superconductor R=0 y α=0
• El valor del parámetro β, en el control titulado Beta.

Se pulsa el botón titulado Nuevo

Observamos el movimiento del imán, las fuerzas sobre el mismo, que en términos de las variables adimensionales son:

• El peso, fuerza constante de valor 1 (hacia abajo)

• La fuerza que ejerce el campo magnético producido por la espira sobre el imán.

${\displaystyle -\frac{3}{2}\frac{x}{{\left(x^2+1\right)}^{5/2}}i}$

Positiva si la corriente i es en el sentido de las agujas del reloj y negativa, en caso contrario.

Los puntos rojos en la espira, representan cargas positivas cuyo movimiento nos sugiere el sentido de la corriente inducida.

En la parte derecha, se representa:

• En color rojo, la intensidad i adimensional de la corriente inducida en la espira

• En color azul, la posición x del imán

En el extremo derecho, un diagrama de barras representa el balance energético.

La energía inicial del imán es x₀

La energía en un instante τ es la suma de la energía

• Potencial gravitatoria del imán, x, en color amarillo

• Cinética del imán, $\frac{1}{2}{\left(\frac{dx}{d\tau }\right)}^2$ , en color azul

• Energía magnética$\frac{1}{2}\frac{i^2}{\beta }$ , en color rojo.

Cuando el imán cae, la energía potencial gravitatoria, se convierte por una parte en energía cinética y por la otra, en energía del campo magnético producido por la espira. Si la espira tiene resistencia, una parte de la energía se disipa en forma de calor por efecto Joule, la energía total (suma de las tres clases de energías) va disminuyendo con el tiempo.

Cuando la espira es superconductora, R=0, y α=0, el imán puede levitar sobre la espira, se mueve hacia abajo y hacia arriba, la energía se conserva, se puede medir el periodo de las oscilaciones. Si la resistencia es pequeña, se observan oscilaciones amortiguadas, cuya amplitud va disminuyendo con el tiempo.

En la siguiente tabla, se sugieren algunos valores de los parámetros α y β, y la posición inicial x₀

Referencias

Belcher J. W. The falling magnet. web.mit.edu/8.02t/www/802TEAL3D/visualizations/resources/fallingMagnetEqs.pdf