Varilla que se mueve en un campo magnético uniforme

Sea un conductor rectilíneo que desliza con velocidad constante v por dos guías tal como se muestra en la figura (más abajo). Las guías están conectadas por uno de sus extremos para formar un circuito cerrado.

La ley de Faraday

Supongamos que el campo magnético $\vec{B}$ es constante y es perpendicular al plano determinado por las guías y la varilla. El flujo del campo magnético a través del circuito de forma rectangular ABCD señalado en la figura es

$Φ = \vec{B} \cdot \vec{S} = B a x$

donde a·x es el área del rectángulo ABCD.

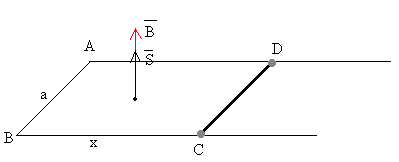
Al moverse la varilla CD la dimensión x del rectángulo aumenta o disminuye, haciendo variar el flujo con el tiempo. De acuerdo a la ley de Faraday, la fem inducida en el circuito ABCD es

$V_{ε} = - \frac{d Φ}{d t} = - B a \frac{d x}{d t} = - B a v$

Si la varilla CD se mueve hacia la derecha dx/dt=v>0. El sentido de la corriente inducida es el de las agujas del reloj.
Si la varilla CD se mueve hacia la izquierda dx/dt=v<0. El sentido de la corriente inducida es contrario al movimiento de las agujas del reloj.

Sentido de la corriente inducida

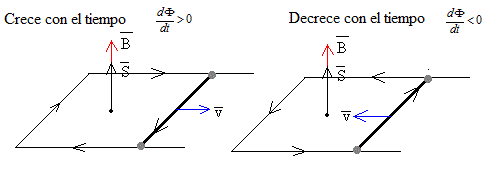
Si la varilla se mueve hacia la derecha, aumenta el área S, lo mismo le ocurre al flujo Φ, el sentido de la corriente inducida es el de las agujas del reloj.
Si la varilla se mueve hacia la izquierda, el área S disminuye, lo mismo le ocurre al flujo Φ, el sentido de la corriente inducida es contrario al de las agujas del reloj.

$i = \frac{B a v}{R}$

Supondremos que la resistencia de la varilla CD es R y los raíles son superconductores

Estudio energético

Cuando circula por la varilla CD una corriente i, el campo magnético B ejerce una fuerza $\vec{F_{m}} = i ({\hat{u}}_{t} \times \vec{B}) L$ . El vector unitario ${\hat{u}}_{t}$ que señala el sentido de la corriente y el campo $\vec{B}$ son mutuamente perpendiculares, la longitud del conductor es a, por lo que el módulo de la fuerza magnética es F_m=iBa. Su sentido es el indicado en la figura (hacia la izquierda si la varilla se mueve hacia la derecha)

Para que la varilla se mueva con velocidad constante v hacia la derecha, hemos de ejercer una fuerza F_a igual y de sentido contrario a F_m.

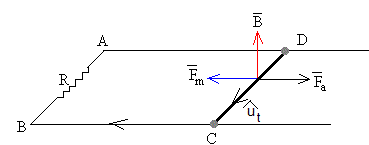
La energía mecánica por unidad de tiempo (potencia) suministrada será

$P_{a} = F_{a} \cdot v = i B a v = \frac{B^{2} a^{2} v^{2}}{R}$

La energía por unidad de tiempo (potencia disipada por efecto Joule) en la resistencia será P_R=i²R

$P_{R} = \frac{B^{2} a^{2} v^{2}}{R}$

En el estado estacionario, la intensidad de la corriente es constante, la energía por unidad de tiempo suministrada mecánicamente al mover la varilla, se disipa en la resistencia en forma de calor.

Si consideramos la varilla como una batería cuya fem es V_ε=vBa. La potencia suministrada por la fem será P_ε=V_ε·i

$P_{E} = \frac{B^{2} a^{2} v^{2}}{R}$

Movimiento de la varilla

Estudiamos el movimiento de la varilla para dos casos particulares:

No se aplica fuerza a la varilla, F_a=0

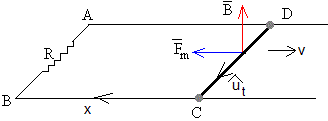
Supongamos que no se ejerce la fuerza mecánica F_a igual a la fuerza magnética de frenado F_m, que mantiene la velocidad contante v de la varilla

La varilla que parte de x=0 con velocidad v₀, irá disminuyendo su velocidad hasta que se detiene en x_m

$m \frac{d v}{d t} = - \frac{B^{2} a^{2}}{R} v$

Teniendo en cuenta que dv/dt=(dv/dx)(dx/dt)=v(dv/dx)

$\begin{array}{l} \frac{d v}{d x} = - \frac{B^{2} a^{2}}{m R} \\ v - v_{0} = - \frac{B^{2} a^{2}}{m R} x \end{array}$

La máxima distancia x_m que recorre hasta detenerse v=0, es

$x_{m} = \frac{m R}{B^{2} a^{2}} v_{0}$

Integrando la ecuación diferencial obtenemos la velocidad de la varilla en función del tiempo

$\begin{array}{l} \int_{v_{0}}^{v} \frac{d v}{v} = - \frac{B^{2} a^{2}}{m R} \int_{0}^{t} d t \\ v = v_{0} \exp (- \frac{B^{2} a^{2}}{m R} t) \end{array}$

La intensidad i de la corriente inducida vale

$i = \frac{B a v}{R} = \frac{B a}{R} v_{0} \exp (- \frac{B^{2} a^{2}}{m R} t)$

Comprobamos que la energía cinética inicial de la varilla $\frac{1}{2} m v_{0}^{2}$ se disipa en la resistencia en forma de calor

$\int_{0}^{\infty} (i^{2} R) d t = {- \frac{B^{2} a^{2}}{R} v_{0}^{2} \frac{m R}{2 B^{2} a^{2}} \exp (- 2 \frac{B^{2} a^{2}}{m R} t) |}_{0}^{\infty} = \frac{1}{2} m v_{0}^{2}$

Se aplica una fuerza constante F_a a la varilla

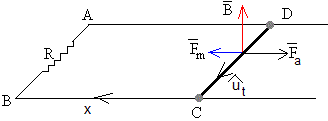
Supongamos que se ejerce una fuerza mecánica F_a constante sobre la varilla que parte de x=0 con velocidad v=0. La varilla irá incrementado su velocidad hasta que alcanza un valor límite constante. La ecuación del movimiento es

$m \frac{d v}{d t} = F_{a} - \frac{B^{2} a^{2}}{R} v$

Integramos la ecuación diferencial, con la condición inicial t=0, v=0

$\begin{array}{l} \int_{0}^{v} \frac{d v}{\frac{F_{a}}{m} - \frac{B^{2} a^{2}}{m R} v} = \int_{0}^{t} d t \\ v = \frac{F_{a} R}{B^{2} a^{2}} (1 - \exp (- \frac{B^{2} a^{2}}{m R} t)) \end{array}$

Después de un tiempo t, teóricamente infinito, la velocidad de la varilla alcanza el valor límite constante, F_aR/(B²a²)

La intensidad i de la corriente inducida vale

$i = \frac{B a v}{R} = \frac{F_{a}}{B a} (1 - \exp (- \frac{B^{2} a^{2}}{m R} t))$

que también alcanza un valor límite constante, F_a/(Ba)

Comprobamos que una parte del trabajo de la fuerza aplicada F_a, incrementa la energía cinética de la varilla y otra parte, se disipa en forma de calor en la resistencia

$\int_{0}^{t} F_{a} (v \cdot d t) = \frac{1}{2} m v^{2} + \int_{0}^{t} (i^{2} R) d t$

El valor del trabajo es

$\int_{0}^{t} F_{a} (v \cdot d t) = \frac{F_{a}^{2} R}{B^{2} a^{2}} {t - \frac{m R}{B^{2} a^{2}} (1 - \exp (- \frac{B^{2} a^{2}}{m R} t))}$

Cuando el tiempo t se hace grande la expresión del trabajo es

$\frac{F_{a}^{2} R}{B^{2} a^{2}} {t - \frac{m R}{B^{2} a^{2}}}$

que es la suma de la energía cinética de la varilla (que se mueve con velocidad límite constante) y la energía disipada en la resistencia

$\frac{1}{2} m {(\frac{F_{a} R}{B^{2} a^{2}})}^{2} + \frac{F_{a}^{2} R}{B^{2} a^{2}} {t - \frac{3}{2} \frac{m R}{B^{2} a^{2}}}$

Actividades

El programa interactivo describe el movimiento de una varilla que desliza sin rozamiento sobre dos guías paralelas. El sistema formado por la varilla y las guías esta contenido en un plano paralelo a los polos de un imán.

Se introduce:

El campo magnético en gauss. Inicialmente el campo magnético apunta en la dirección vertical, hacia arriba. Si introducimos un valor negativo, se cambia la polaridad de los imanes y el campo magnético apunta hacia abajo.
La velocidad de la varilla en cm/s. Este valor puede ser positivo o negativo. Si es positivo la varilla se mueve de izquierda a derecha y si es negativo se mueve de derecha a izquierda.
La distancia entre las guías en cm. Un número menor que 15.

Se pulsa el botón titulado Nuevo.

La corriente inducida se representa mediante el movimiento de pequeños círculos de color rojo (portadores de carga positivos).

Observar que el vector campo (flecha de color azul) se mantiene constante, pero el vector superficie (flecha de color negro) va cambiando a medida que se mueve la varilla.

Ejemplo:

B=40 gauss=0.004 T
v=5 cm/s=0.05 m/s
a=10 cm=0.1 m

La fem vale V_є=0.04·0.05·0.1=2·10^-5 V

Campo magnético:
Velocidad:
Distancia raíles:

Dos varillas que se mueven en un campo magnético uniforme

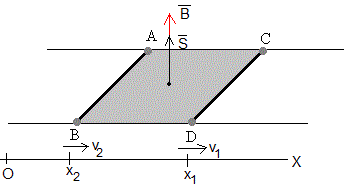
Consideremos dos varillas conductoras de masas m₁ y m₂ y resistencias R₁ y R₂. Las varillas deslizan sin rozamiento sobre dos carriles superconductores paralelos distantes a. En un instante dado t, la posición de la primera varilla es x₁ y su velocidad v₁, la posición de la segunda varilla es x₂ y su velocidad v₂.

El flujo del campo magnético a través del circuito ABDC es

$Φ = \vec{B} \cdot \vec{S} = B (x_{1} - x_{2}) a$

La fem es

$V_{ε} = - \frac{d Φ}{d t} = - B a (\frac{d x_{1}}{d t} - \frac{d x_{2}}{d t})$

Si v₁ es mayor que v₂, la corriente inducida tiene el sentido de las agujas del reloj

$i = \frac{B a}{R_{1} + R_{2}} (v_{1} - v_{2})$

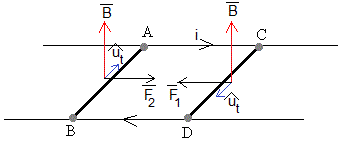
El campo magnético ejerce una fuerza sobre la corriente inducida en cada una de las varillas

$\vec{F_{m}} = i ({\hat{u}}_{t} \times \vec{B}) L$

Las fuerzas F₁ y F₂ son iguales y de sentido contrario, su módulo es

$F = \frac{B^{2} a^{2}}{R_{1} + R_{2}} (v_{1} - v_{2})$

Ecuaciones del movimiento

Tenemos un sistema similar al de dos cuerpos bajo la acción de la fuerza de interacción mutua

Las ecuaciones del movimiento de cada una de las varillas son

$\begin{array}{l} m_{1} \frac{d v_{1}}{d t} = - \frac{B^{2} a^{2}}{R_{1} + R_{2}} (v_{1} - v_{2}) \\ m_{2} \frac{d v_{2}}{d t} = \frac{B^{2} a^{2}}{R_{1} + R_{2}} (v_{1} - v_{2}) \end{array}$

Movimiento del centro de masas

Sumando ambas ecuaciones

$\frac{d (m_{1} v_{1} + m_{2} v_{2})}{d t} = 0$

El momento lineal total de las dos varillas se mantiene constante e igual al momento lineal inicial,

m₁v₁+m₂v₂=m₁v₀₁+m₂v₀₂

Movimiento relativo

Restamos dv₂/dt-dv₁/dt

$\begin{array}{l} {\begin{cases} \frac{d v_{1}}{d t} = - \frac{B^{2} a^{2}}{m_{1} (R_{1} + R_{2})} (v_{1} - v_{2}) \\ \frac{d v_{2}}{d t} = \frac{B^{2} a^{2}}{m_{2} (R_{1} + R_{2})} (v_{1} - v_{2}) \end{cases} \\ \frac{d (v_{2} - v_{1})}{d t} = - (k_{2} + k_{1}) (v_{2} - v_{1}) \\ \frac{d v_{21}}{v_{21}} = - (k_{2} + k_{1}) d t \end{array}$

Integramos

$\begin{array}{l} \int_{v_{02} - v_{01}}^{v_{2} - v_{1}} \frac{d v_{21}}{v_{21}} = - (k_{2} + k_{1}) \int_{0}^{t} d t \\ v_{2} - v_{1} = (v_{02} - v_{01}) \exp (- (k_{2} + k_{1}) t) \end{array}$

La velocidad relativa decrece exponencialmente con el tiempo.

Movimiento de cada varilla

Combinando esta ecuación con la de la constancia del momento lineal, despejamos v₁ y v₂

$\begin{array}{l} v_{2} = \frac{m_{1} v_{01} + m_{2} v_{02}}{m_{1} + m_{2}} - \frac{m_{1} (v_{01} - v_{02})}{m_{1} + m_{2}} \exp (- (k_{2} + k_{1}) t) \\ v_{1} = \frac{m_{1} v_{01} + m_{2} v_{02}}{m_{1} + m_{2}} + \frac{m_{2} (v_{01} - v_{02})}{m_{1} + m_{2}} \exp (- (k_{2} + k_{1}) t) \end{array}$

Conocida la velocidad v de cada varilla en función del tiempo, integramos para calcular su posición x

$\begin{array}{l} x_{2} = x_{02} + \frac{m_{1} v_{01} + m_{2} v_{02}}{m_{1} + m_{2}} t - \frac{m_{1} (v_{01} - v_{02})}{(m_{1} + m_{2}) (k_{2} + k_{1})} (1 - \exp (- (k_{2} + k_{1}) t)) \\ x_{1} = x_{01} + \frac{m_{1} v_{01} + m_{2} v_{02}}{m_{1} + m_{2}} t + \frac{m_{2} (v_{01} - v_{02})}{(m_{1} + m_{2}) (k_{2} + k_{1})} (1 - \exp (- (k_{2} + k_{1}) t)) \end{array}$

Caso particular

Supongamos que las varillas son iguales m₁=m₂=m, R₁=R₂=R.

$\begin{array}{l} {\begin{cases} v_{2} = \frac{v_{01} + v_{02}}{2} - \frac{v_{01} - v_{02}}{2} \exp (- 2 k t) \\ v_{1} = \frac{v_{01} + v_{02}}{2} + \frac{v_{01} - v_{02}}{2} \exp (- 2 k t) \end{cases} \\ {\begin{cases} x_{2} = x_{02} + \frac{v_{01} + v_{02}}{2} t - \frac{v_{01} - v_{02}}{4 k} (1 - \exp (- 2 k t)) \\ x_{1} = x_{01} + \frac{v_{01} + v_{02}}{2} t + \frac{v_{01} - v_{02}}{4 k} (1 - \exp (- 2 k t)) \end{cases} \\ k = \frac{B^{2} a^{2}}{2 m R} \end{array}$

Ejemplo

La velocidad inicial de la primera varilla es, v₀₁= 3 m/s
La velocidad inicial de la segunda varilla es, v₀₂= 1 m/s
Asignamos al parámetro el valor k=0.5 s^-1

Representamos la velocidad de cada varilla en función del tiempo

v02=1; %velocidad inicial 
v01=3; %velocidad inicial 
k=0.5; %parámetro

v2=@(t) (v01+v02)/2-(v01-v02)*exp(-2*k*t)/2;
v1=@(t) (v01+v02)/2+(v01-v02)*exp(-2*k*t)/2;
hold on
fplot(v2,[0,5])
fplot(v1,[0,5])
hold off
grid on
xlabel('t')
ylabel('v')
legend('v_2','v_1')
title('velocidad')

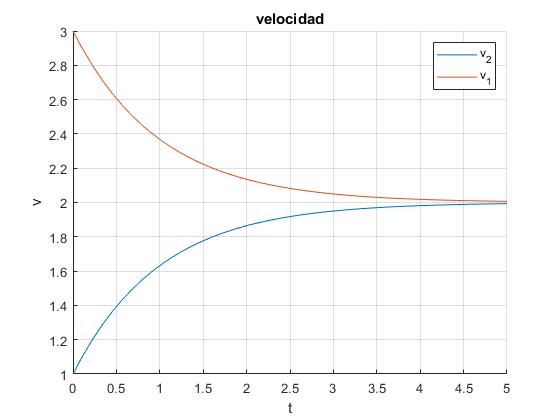
La velocidad de la primera varilla decrece, la de la segunda varilla crece hasta que ambas tienden (cuando t→∞) a la velocidad constante del centro de masas (v₀₁+v₀₂)/2

Balance energético

La variación de energía cinética entre t=0 y t→∞

$\begin{array}{l} E_{k i} = \frac{1}{2} m v_{01}^{2} + \frac{1}{2} m v_{02}^{2} \\ E_{k f} = \frac{1}{2} m {(\frac{v_{01} + v_{02}}{2})}^{2} + \frac{1}{2} m {(\frac{v_{01} + v_{02}}{2})}^{2} = \frac{1}{4} m {(v_{01} + v_{02})}^{2} \\ E_{k f} - E_{k i} = - \frac{1}{4} m {(v_{01} - v_{02})}^{2} \end{array}$

La energía disipada en las dos resistencias

$\begin{array}{l} i = \frac{B a}{2 R} (v_{1} - v_{2}) = \frac{B a}{2 R} (v_{01} - v_{02}) \exp (- 2 k t) \\ E_{R} = \int_{0}^{\infty} i^{2} (2 R) \cdot d t = \frac{B^{2} a^{2}}{2 R} {(v_{01} - v_{02})}^{2} \int_{0}^{\infty} \exp (- 4 k t) \cdot d t = \frac{1}{4} m {(v_{01} - v_{02})}^{2} \end{array}$

Parte de la energía cinética se disipa en las resistencias

Referencias

Del apartado 'Dos varillas que se mueven en un campo magnético uniforme'

Ker Liang Goh, Koo Feng Goh, Motion of a two-rod conducting circuit in a magnetic field. Phys. Educ. 55 (2020) 023001